Всем привет. Мы продолжаем серию статей о том, какие ответы может дать data science о прогнозировании COVID-19. Первая статья здесь (ссылка). Сегодня поговорим о втором классе моделей по предсказанию динамики распространения COVID-19. Они основаны на предположениях о росте заболеваемости и описывают ситуацию в средне- и долгосрочной перспективе. Беседуем с Николаем Кобало, старшим инженером данных ЦФТ.
Напомним, какие у нас условия:
Дано: Колоссальные возможности data science, три талантливых специалиста.
Найти: Способы предсказать распространение COVID-19 на неделю вперёд.
— Коля, привет. Расскажи, какую модель ты использовал для решения этой задачи.
— Я взял одну из моделей, которая, на мой взгляд, лучше всего подходит к случаю. Модель представлена в виде дифференциального уравнения и состоит из четырех функций:
1. Количество людей, которые подвержены заражению данной инфекцией;
2. Количество носителей, то есть людей, которые уже заразились, но ещё не знают об этом;
3. Количество больных людей, которые заражают других;
4. Количество выздоровевших.
Как видим, эта модель не учитывает смертность от ковида. Подробности работы модели можно посмотреть у меня на гитхабе: https://github.com/rerf2010rerf/COVID-19-forecast/blob/master/public.ipynb
Модель называется SEIR и относится к семейству полигамных (англ. compartmental) моделей, описывающих распространение эпидемии. Модели этого семейства позволяют описывать различные типы инфекций. Например, такие, для которых вырабатывается (или, напротив, не вырабатывается) иммунитет. Или те, что имеют (или не имеют) инкубационный период. В случае с COVID-19 я воспользовался моделью с инкубационным периодом и вырабатывающимся иммунитетом у переболевших людей.
Все полигамные модели представляют собой системы дифференциальных уравнений первого порядка. Для SEIR они выглядят так:

Здесь:
S(t) — (Susceptible) – количество людей, подверженных заражению.
E(t) — (Exposed) – количество носителей, т.е. заражённых людей, у которых болезнь еще не проявилась из-за инкубационного периода.
I(t) — (Infectious) – инфицированные.
R(t) — (Recovered) – выздоровевшие.
N = S + E + I + R – численность популяции. Она сохраняется постоянной, т.е. предполагается, что от болезни никто не умирает.
μ – уровень естественной смертности.
α – величина, обратная инкубационному периоду заболевания.
γ – величина, обратная среднему времени выздоровления.
β – коэффициент интенсивности контактов, приводящих к заражению.
Жизненный цикл индивида в SEIR модели выглядит так:

Здоровый, но ещё не переболевший человек (Susceptible) может заразиться от инфицированного (Infectious) человека. Вероятность, с которой здоровый человек заразится, описывается параметром β.
Заразившийся человек переходит в состояние носителя инфекции (Exposed). Носители — это люди, у которых заболевание ещё не проявилось, то есть у них протекает инкубационный период. Носители не могут никого заразить. Переход подверженных заболеванию людей в состояние носителей описывается двумя первыми уравнениями модели (посредством слагаемого β(I/N)).
Через 1/α дней (инкубационный период) после заражения носитель переходит в состояние инфицированного (Infectious).
Через 1/γ дней (время выздоровления) инфицированный переходит в состояние выздоровевшего (Recovered). У выздоровевшего человека вырабатывается иммунитет, и он больше не может заразиться этой инфекцией.
Также модель предусматривает естественную смертность населения в популяции. Смертность в SEIR модели сбалансирована рождаемостью, поэтому общая численность населения не меняется. При этом количество выздоровевших людей в популяции будет уменьшаться, так как новорождённые не будут иметь иммунитета. Соответственно, количество выздоровевших людей в популяции уменьшается со временем. Интенсивность смертности описывается параметром μ.
— У тебя есть коэффициенты в модели. То есть ты делал какие-то предположения?
— Одно из моих предположений заключалось в том, что естественной смертностью в популяции можно пренебречь, т.е. μ = 0. Это предположение кажется допустимым, так как мы хотим предсказывать распространение инфекции на коротком промежутке времени, всего несколько месяцев.
Кроме того, выбранная модель предполагает, что у переболевших появляется иммунитет к инфекции, то есть повторно они не могут заразиться.
— А это так, кстати?
— Вроде как, да. Сейчас уже зафиксировано несколько повторных заражений, но чаще всего этого не происходит. Поэтому, можно сказать, что это так.
— А что такое «коэффициент интенсивности контакта» у тебя?
— Здесь я имею ввиду интенсивность, с которой люди контактируют друг с другом и заражаются. Грубо говоря, это вероятность того, что при встрече двух человек, где один заражён, а другой – нет, второй в итоге заболеет.
— Ну это сколько? Близко к единице?
— Нет, этот параметр я подбирал по данным. Он зависит от уровня самоизоляции. Например, если большая часть населения не вступает в контакт с другими людьми, то коэффициент становится меньше, а если население активно коммуницирует друг с другом, то он вырастает.
— Окей. А время выздоровления тоже у тебя есть? И альфа, и гамма?
— Альфу я брал равной 1/5.1, это известный параметр был для COVID-19 (параметр, обратный инкубационному периоду в днях). А гамму я подбирал по данным. Это «время выздоровления». «Интенсивность контактов», кстати, тоже по данным.
— Ну хорошо. Ещё раз тогда можешь рассказать, какие предположения делаются у моделей? Что каждое уравнение значит?
— Первое уравнение описывает изменение количества подверженных заражению. В частности, третье слагаемое говорит, что чем интенсивнее контакты между зараженными и подверженными, тем быстрее убывает количество подверженных. При этом, если кто-то был подвержен заражению, а потом заразился, то он больше не входит в это количество. В начале эпидемии оно равно количеству людей в популяции.
Потом количество носителей берётся из подверженных заражению, то есть человек общается с заразившимся, заражается и становится носителем заражения. Это описывается во втором уравнении. Оно говорит, что скорость прироста носителей тем больше, чем интенсивнее контакты между подверженными и заражёнными и, напротив, тем меньше, чем меньше осталось носителей в данный момент.
Третье уравнение говорит, что скорость прироста заражённых тем больше, чем больше сейчас есть носителей (которые и превращаются в заражённых), и тем меньше, чем больше заражённых уже есть.
Четвёртое уравнение описывает скорость прироста выздоровевших, которая тем больше, чем больше заражённых (которые могут выздороветь), и тем меньше, чем больше выздоровевших уже есть.
— Звучит как описание развития ситуации.
— На самом деле, есть разные модели. Это SEIR модель, а есть SIR, в которой нет подверженных заражению. Есть модели с бОльшим количеством параметров. Есть модель, в которой предусматривается смертность от заражения, но я её не стал использовать.
— Где нашёл эту модель?
— Погуглил. В Википедии есть статья. Нашёл дополнительно статьи.
— Ты ещё графики представлял.
— Этот график — пример. Он не на основе реальных данных. Здесь просто показано, как ведёт себя модель. Она предсказывает, что все в итоге переболеют и выздоровеют.

— Окей, значит, ты взял всё это, и что дальше?
— Взял данные, которые есть по странам. Предположил, что смертность равна нулю. Переписал дифуры в форму конечных разностей:

В качестве оператора конечной разности в этом решении использована двусторонняя разность.
Количество выздоровевших людей R по дням есть в исходных данных, а количество инфицированных I равно количеству подтверждённых случаев минус количество выздоровевших. Так что из последнего уравнения можно найти γ с помощью оптимизации целевой функции MALE (ΔR-γI).
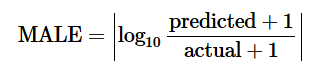
Для того чтобы проследить, как карантинные мероприятия влияют на развитие эпидемии, я немного усложнил себе задачу и заменил коэффициент β на функцию β(t) – ведь по мере того, как в стране вводится карантин, интенсивность заражений должна падать, а значит, в нашем случае β не будет константой. Так как у нас уже есть все начальные условия для решения дифура, можно воспользоваться оптимизацией для поиска функции β(t).
— Это за день разности?
— День минус предыдущий день. Я подставил данные и подсчитал неизвестные коэффициенты.
— Бэта и гамма?
— Альфу я принял 5,1 дня. Соответственно, надо было найти бэта и гамма – интенсивность контактов и время выздоровления.
— И что у тебя вышло?
— Есть графики. Для каждого региона и каждой страны получалось своё. Я решал для каждой страны по отдельности. Слева график данных (чёрное — было реально, красное — заражённые и переболевшие, предсказанные моделью). Заражённые + переболевшие — получается E+R. Справа график коэффициента бэта. Бэта, кстати, предполагается, что зависит от времени. Здесь самый большой скачок в β совпадает со временем введения карантина 30 марта.
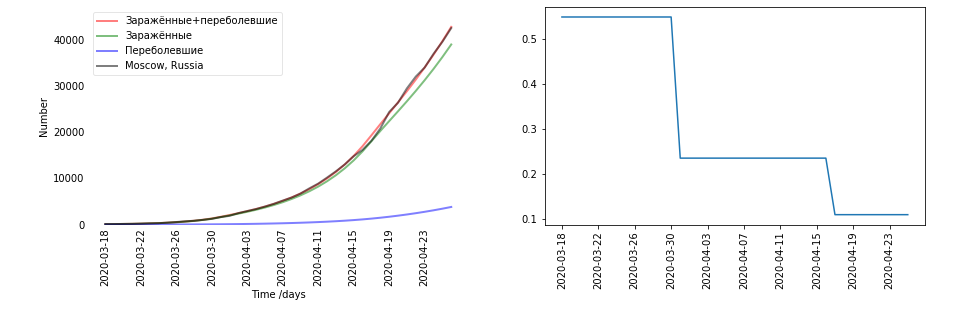
— А это ты по данным посчитал или предположил так?
— Это уже по данным посчитано. Это как раз результат обучения на Москве.
— А временные пороги ты сам устанавливал?
— Я считал, что функция имеет такой двухступенчатый вид. И оптимизировал. Просто подгонял по данным и находил оптимальные функции, которые лучше всего подходят. Также я пробовал использовать функции с другим количеством ступенек, но двухступенчатые показали лучшие результаты.
— Давай на страны посмотрим, допустим, Италия. Ну тут у тебя другая картинка…

— В Италии карантин, видимо, лучше сработал. И переболевших там больше. Модель подтвердила, что 9 марта был введён карантин.
— Что ты выбрал для финального прогноза?
— Для финального прогноза я выбрал константную интенсивность контактов и по двум последним точкам строил модель. То есть знаем всю предыдущую историю, но берём только последние точки.
— Это для предсказания на неделю?
— Да. А что до этого было — это посмотреть, как модель себя ведёт. А дальше уже смотрел, какую функцию лучше брать и на скольких точках обучаться.
— Наверное, если бы ты хотел спрогнозировать до сегодняшнего момента, ты бы другое решение получил. А у тебя есть что-то такое, что покажет, как дальше может ситуация развиваться?
— Да. Но там не очень интересно. Предсказывала, что к сентябрю в Москве переболеют все.
— На одном из митапов ты говорил, что по твоему прогнозу пик должен был быть в июле. По факту все произошло немного раньше. Как думаешь, что модель не учла?
— Возможно, бета. Возможно, карантин усилился. Возможно, интенсивность контактов снизилась из-за того, что люди переболели, и не заражают, и не заражаются. Бэта должна как-то и от этого зависеть. А здесь это не учитывается.
— Ну то есть ты говоришь, что всё можем регулировать одной бэтой?
— По известным данным — да, можем, бэтой и гаммой подогнать.
— Твоя модель предсказывает очередную волну?
— Нет, всё стабильно: растёт, растёт, растёт и все переболеют. Хотя есть ещё фактор сезонности. Осенние периоды, например, (когда грипп и т.п., иммунная система ослабляется). Но всё это модель не учитывает.
— Какие можешь выделить плюсы и минусы своей модели?
— На период составления модели было немного известных данных. Сейчас уже известны и период восстановления, и инкубационный период (тогда 5.1 был, сейчас более точно измерили). Из плюсов: она показывает сам процесс, как это протекает. И если исследовать более глубоко на примере других стран, например, Италии, Германии, как эти бэты влияли, то можно было бы для нас эту модель уточнить и построить более точный долгосрочный прогноз.
Похоже, в эпидемиологической модели data science – это подбор коэффициентов по данным.
Представленная модель учит нас анализу, моделированию ситуации и тому, как делать предположения. Для причинно-следственного анализа – это необходимый навык, как и для долгосрочного прогноза, так как модель машинного обучения, рассмотренная в первой статье, очень сильно бы уползла с накоплением ошибки.
Однако для краткосрочного прогноза, похоже, нет альтернативы машинному обучению. В следующей статье мы побеседуем
Заголовок спойлерас Александром Желубенковым: он сделал самую крутую модель 😉
ссылка на оригинал статьи https://habr.com/ru/company/cft/blog/544492/
Добавить комментарий