Почему?
Я уже два с половиной года пишу на Js, и почти повсюду вижу примеры решения типовых задач для этого языка . Отрисовать очередную онлайн-витрину, подать асинхронный запрос на бек за очередным JSON. Уровнем повыше — построить структуру данных для SPA и на ее основе отобразить визуальные компоненты. Но в Js есть полноценная библиотека математических функций, он обеспечивает неплохую для скриптового языка скорость вычислений (здесь сравнение производительности по бенчмаркам Питона vs Node ), так что почему бы не попытаться сделать еще один шаг и не решить с его помощью какую-нибудь инженерную задачу. Например — из космической области.
Постановка задачи
Моделируется движение летательного аппарата в центральном поле тяготения, Земля — шар радиусом в 6.3711E+6 м, параметр гравитационного колодца — 0.398E+15 Н * м2/кг рассматривается движение материальной точки (в следующих итерациях может появиться анализ движения вокруг центра масс), управление ЛА осуществляется через изменение программного угла атаки и регулирование тяги двигателя.
Сила лобового сопротивления всегда направлена против вектора скорости ЛА, подъемная сила — по нормали к вектору скорости. Атмосферу определим кусочно-линейной интерполяцией из Стандартной Атмосферы ГОСТ 4401-81.
Обыкновенные дифференциальные уравнения движения точки в центральном поле тяготения интегрируются методом Эйлера-Коши второго порядка точности (он же — усовершенствованный метод Эйлера).
Заглянуть на текущее состояние проекта можно здесь: satMod на гитхабе.
How to use?
Вызвать консоль и указать ей node launcher.js
Спустя некоторое время в консоли появится сообщение о проведенном расчете с указанием потраченного в миллисекундах времени. А рядом появится csv-файл с результатами. Расшифровка следующая — время(с), скорость (м/с), высота (м), пройденный путь (м), масса (кг), продольные и поперечные ускорения от внешних сил (кроме силы тяжести, м/с2), расход массы (кг), число M, скоростной напор (Па), координаты радиус-вектора (X, Y, м) и вектора скорости (Vx, Vy, м/с) в глобальной системе координат, связанной с центром Земли (или любой другой выбранной планеты)
К сожалению, пока что обрабатываемый вариант и условия окончания интегрирования жестко забиты в launcher.js, так что если хочется посчитать что-то кроме дефолтного варианта, то придется вносить правки в launcher
Зачем нужна такая модель?
Можно оценить параметры выведения, когда точности метода сумм скоростей Циолковского с вычетом потерь на гравитацию, сопротивление и неоптимальный режим ДУ уже недостаточно. Можно оценивать аэродинамические маневры в атмосфере — аэроторможение, планирование и глиссирование (Зенгер-стайл) на входе в атмосферу, а затем — и тепловые нагрузки на обшивку летательного аппарата. Или рассчитывать сбор гелия-3 скиммером с ядерно-прямоточным двигателем в верхних слоях атмосферы Урана с последующим подъемом до танкера на низкой орбите.
Компоненты модели
Основная магия модели происходит в модулях vehicleStage и compositeVehicle. Первый заведует поведением отдельной ступени ЛА и вычислением производных для системы ОДУ баллистической задачи, второй — комбинирует несколько ступеней в единое целое и управляет схемой действия ЛА
1. класс vehicleStage, метод формирования производных
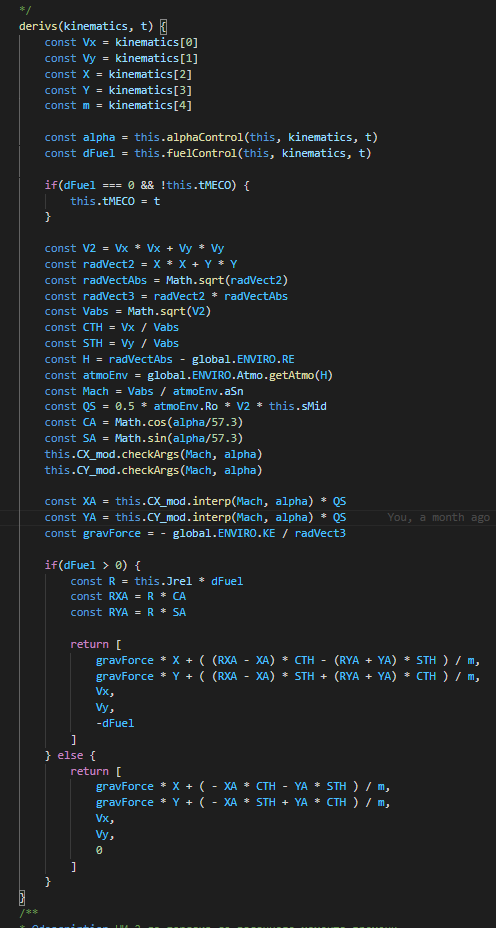
2. класс compositeVehicle. Управление данными многоступенчатого ЛА

Проверка возможностей. «Гагаринский кейс»
Начнем с самого простого кейса — круговой околоземной орбиты. Для высоты в 200 км первая космическая скорость составит 7788.14 м/с, а период обращения — 5301 с. Пренебрежем влиянием атмосферы и запустим программу исходными данными V = 7788 м/с, Th = 0.00 град, H = 200000 м и посмотрим, куда после 5300 секунд интегрирования прилетит наш спутник. Поскольку продолжительность интегрирования велика, а порядок метода интегрирования — второй, то ошибки будут неизбежны, однако они не исказят качественно картину решения
Начальная точка траектории
|
t,c |
V, м/с |
Th, град |
H, км |
L, км |
X, м |
Y, м |
|
0 |
7788.1 |
0.00 |
200 |
0 |
0 |
6571100 |
|
0.5 |
7788.1 |
0.00 |
200 |
0.38 |
3894 |
6571099 |
Конечная точка (без атмосферы)
|
t,c |
V, м/с |
Th, град |
H, км |
L, км |
X, м |
Y, м |
|
5301.0 |
7788.1 |
0.00 |
200 |
0 |
-2428 |
6571100 |
|
5301.5 |
7788.1 |
0.00 |
200 |
0.14 |
1466 |
6571100 |
Конечная точка (атмосфера)
|
t, с |
V, м/с |
Th, град |
H, км |
L, км |
X, м |
Y, м |
|
5300.5 |
7788.6 |
0.00 |
199.25 |
40028 |
-2787 |
6570349 |
|
5301.0 |
7788.6 |
0.00 |
199.25 |
1.07 |
1107 |
6570349 |
В идеальной «безатмосферной» постановке задачи спутник прошел полный круг и вернулся в начальную точку с той же высотой и скоростью в пределах десятых долей секунды от теоретической цифры для круговой орбиты. В «атмосферной» постановке остаточный скоростной напор за 5300 секунд чуть-чуть (на 750 м) снизил орбиту. Так что еще одна область применения — быстрая оценка затухания орбиты, в том числе через управление площадью и ориентацией спутника. Надувные баллюты, паруса, баллоны вроде ретрансляторов Echo.
Возвращение на Землю
Усложним задачу и введем тормозной импульс спустя 500 секунд полета, после чего посмотрим, как наш ИСЗ начнет погружение в атмосферу (этот вариант исходных данных значится как simple_sat.json среди ИД). Небольшой ракетный двигатель с удельным импульсом в 255 с (пусть это тормозной РДТТ) и запасом топлива в 150 кг сбросит нам 263 м/с
Пик торможения, максимальные перегрузки (~ 10g)
|
t, с |
V, м/с |
Th, град |
H, км |
L, км |
aX, м/c2 |
Q, Па |
|
1255.3 |
3947.1 |
-5.36 |
37.4 |
9278 |
-98.53 |
49271 |
|
1255.8 |
3898.2 |
-5.42 |
37.21 |
9278 |
-98.62 |
49310 |
|
1256.3 |
3849.4 |
-5.47 |
37.03 |
9281 |
-98.6 |
49299 |
Торможение почти завершено. Дозвук
|
t, с |
V, м/с |
Th, град |
H, км |
L, км |
aX, м/c2 |
Q, Па |
|
1361.8 |
168.6 |
-80.06 |
9.96 |
9385 |
-11.82 |
5907 |
|
1445.3 |
91.4 |
-90.00 |
-0.009 |
9385 |
-10.24 |
5114 |
Проверим адекватность расчет сопротивления и сравним полученную скорость с аналитическим значением установившейся скорости (m = 1100 кг, Cxa = 0.8, S = 2.75 м2, Ro = 1.15 кг/м3)
Установившаяся скорость падения для высоты 0 ~ 1000м составит 90.7 — 92.4 м/с, что хорошо согласуется с полученной численным интегрированием скоростью снижения в конце участка снижения. На весь расчет от начала витка до спуска ушло 57 миллисекунд.
Выводы: Модель позволяет рассчитывать движение ИСЗ в центральном поле тяготения с учетом аэродинамического торможения и работы ДУ ИСЗ. Хорошим направлением развития будет оценка управляемого входа в атмосферу Земли с использованием подъемной силы, а также расчет аэроторможения в атмосфере другой планеты (Марс?).
Но это уже в следующих выпусках.
ссылка на оригинал статьи https://habr.com/ru/post/548848/
Добавить комментарий