Экспериментально подтверждается, что элементарная частица должна превысить скорость света, если квантовомеханическим образом «туннелирует» через стену.
Едва только были открыты радикальные уравнения квантовой механики, физики обнаружили один из страннейших феноменов, допускаемых этой теорией.
«Квантовое туннелирование» демонстрирует, сколь глубоко отличаются элементарные частицы, например, электроны, от макроскопических объектов. Например, бросьте мяч о стену – и он отскочит. Дайте ему скатиться на дно ложбинки, и он останется там. Но частица в первом случае может случайно проскочить сквозь стену. У частицы есть шанс «проскользнуть через гору и выкатиться из ложбинки», как написали в журнале Nature двое физиков в 1928 году, в одной из самых ранних характеристик квантового туннелирования.
Физики быстро обнаружили, что способность частиц туннелировать сквозь барьеры позволяет разрешить многие тайны. Эта способность объясняет и различные химические связи, и радиоактивный распад, и термоядерный синтез в недрах Солнца, где ядрам водорода удается преодолеть взаимное отталкивание и слиться – в результате чего возникает солнечный свет.
Но физиков одолело любопытство, сначала умеренное, а потом по-настоящему болезненное. Сколько же времени требуется частице, чтобы туннелировать сквозь барьер?
Проблема заключалась в том, что ответ получался бессмысленным.
Первые ориентировочные подсчеты времени туннелирования были опубликованы в 1932 году. Возможно, в частных разговорах такие оценки делались даже раньше, но «когда получаешь ответ, с виду не имеющий смысла, ты его не публикуешь», — отмечает Эфраим Стейнберг, физик из Университета Торонто.
Только в 1962 году инженер Томас Хартман из «Texas Instruments» написал статью, в которой открыто принимал шокирующие выводы, проистекавшие из математики.
Хартман обнаружил, что по принципу действия барьер напоминает короткое замыкание. Когда частица туннелирует, она тратит на перемещение меньше времени, чем если бы барьер отсутствовал. Еще поразительнее оказалось вот что: он рассчитал, что при утолщении барьера практически не увеличивается время, нужное частице, чтобы через него туннелировать. Таким образом, при наличии достаточно толстого барьера частица могла бы перескочить с одной его стороны на другую быстрее, чем свет преодолел бы то же расстояние в вакууме.
Короче говоря, квантовое туннелирование открывает возможность для сверхсветовых перемещений, которые, казалось бы, в физике не допускаются.
“Настоящие поводы для беспокойства появились только после открытия эффекта Хартмана,” – сказал Стейнберг.
Эта дискуссия закручивалась десятилетиями, отчасти потому, что вопрос о времени туннелирования затрагивает один из наиболее загадочных аспектов квантовой механики. «Отчасти он касается общей проблемы, которая позволила бы понять, что такое время, и как время измеряется в квантовой механике, и что это значит,” сказал Илай Поллак, физик-теоретик из Института Вейцмана в Израиле. Со временем физики вывели не менее 10 альтернативных математических выражений, описывающих туннелирование во времени, и каждое из них отражает свой взгляд на процесс туннелирования. Ни один из этих вариантов не позволил решить проблему.
Но сегодня вопрос о том, как соотносится туннелирование и время, вновь обретает актуальность, благодаря серии виртуозных экспериментов, позволивших точно измерить время туннелирования в лаборатории.

Эфраим Стейнберг, физик из университета Торонто. Занимается проблемой времени туннелирования уже не одно десятилетие.
Фото Мэтью Росса
Измерительный опыт, получивший наиболее высокую оценку на настоящий момент, был описан в одной из публикаций в июльском номере журнала Nature. Группа Стейнберга из университета Торонто воспользовалась методом под названием «часы Лармора», чтобы оценить, как атомы рубидия туннелируют через лазерное поле, в котором действуют силы отталкивания.
“Часы Лармора – наилучший и наиболее понятный способ измерить время туннелирования, и это был первый эксперимент, в рамках которого это время удалось очень хорошо измерить,” сказал Игорь Литвинюк, физик из университета Гриффита в Австралии, описавший иную попытку такого измерения времени туннелирования и также опубликовавший статью в журнале Nature.
Луис Манзони, физик-теоретик из Конкордия-Колледж, штат Миннесота, также находит убедительными измерения с применением часов Лармора. «Они в самом деле измеряют время туннелирования,” – говорит он.
Последние эксперименты вновь привлекают внимание к нерешенной проблеме. С момента публикации статьи Хартмана минуло шесть десятилетий, и независимо от того, как тщательно физики переопределяли время туннелирования или с какой точностью измеряли его в лаборатории, неизменно обнаруживалось, что при квантовом туннелировании проявляется эффект Хартмана. Представляется, что туннелирование является неисправимо, непоколебимо сверхсветовым процессом.
Литвинюк предлагает задуматься, “как это возможно, чтобы [туннелирующая частица] двигалась быстрее света?” и отмечает, что “это была чистая теория, пока не были выполнены измерения.”
Сколько времени?
Время туннелирования сложно зафиксировать, как и понять, что такое реальность.
В макроскопических масштабах время, затрачиваемое объектом для перехода из точки A в точку B, можно узнать, просто разделив расстояние на скорость объекта. Но в квантовой теории невозможно одновременно точно знать расстояние и скорость.
В квантовой теории у частицы есть целый спектр возможных местоположений и скоростей. Определенные варианты из всех этих возможностей в момент измерения словно кристаллизуются. Как именно это происходит – один из глубочайших вопросов.
Суть в том, что, пока частица не попадет в детектор, она одновременно находится везде и нигде. Поэтому весьма сложно сказать, сколько времени частица провела где-либо до попадания в детектор, например, внутри барьера. «Нельзя сказать, сколько времени она там проводит», — говорит Литвинюк, так как она может быть в двух местах одновременно.
Чтобы понять эту проблему в контексте туннелирования, начертим колоколообразную кривую, соответствующую всем возможным местоположениям частицы. Такая кривая, называемая «волновым пакетом», центрирована по позиции А. Теперь изобразим перемещение волнового пакета по направлению к барьеру, он при этом будет выглядеть как цунами (или как солитон? – прим. пер.). Уравнения квантовой механики описывают, как волновой пакет раздваивается при столкновении с препятствием. Большая часть пакета отражается и направляется обратно к А. Но меньший пик вероятности проскальзывает сквозь барьер и продолжает движение к B. Следовательно, существует шанс, что детектор зарегистрирует частицу в B.
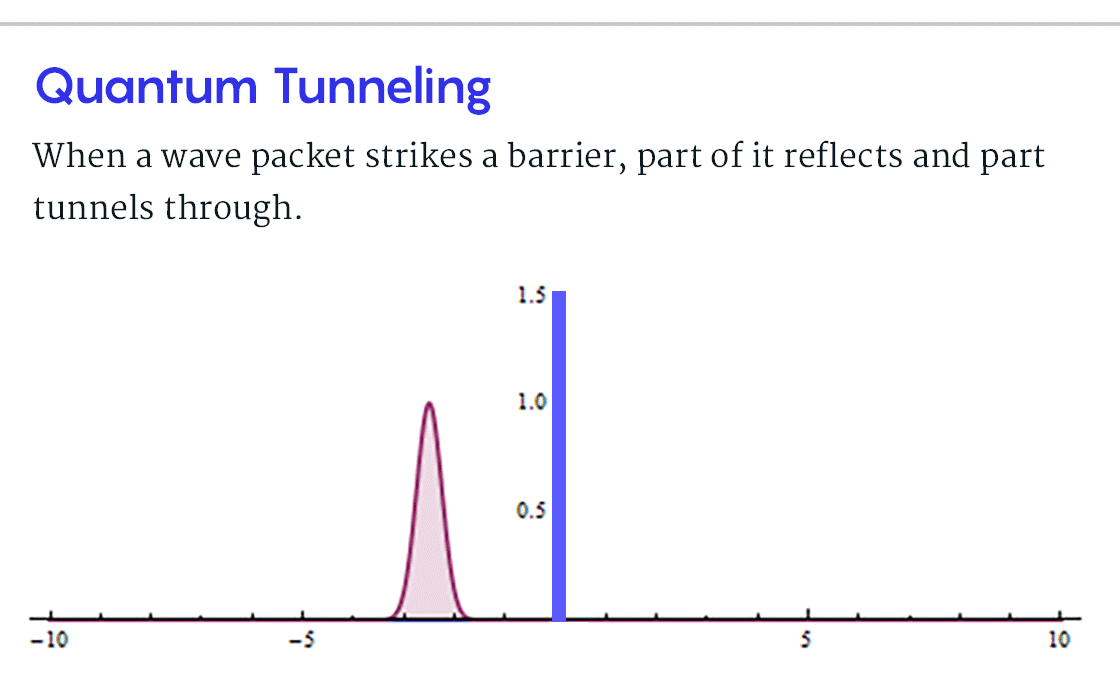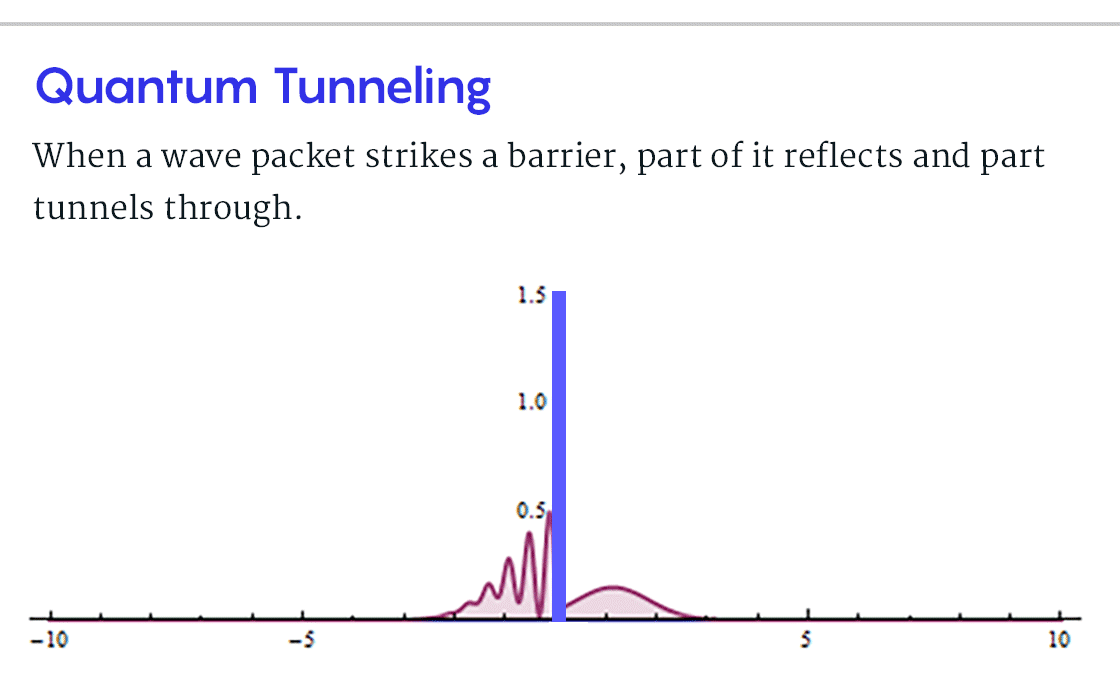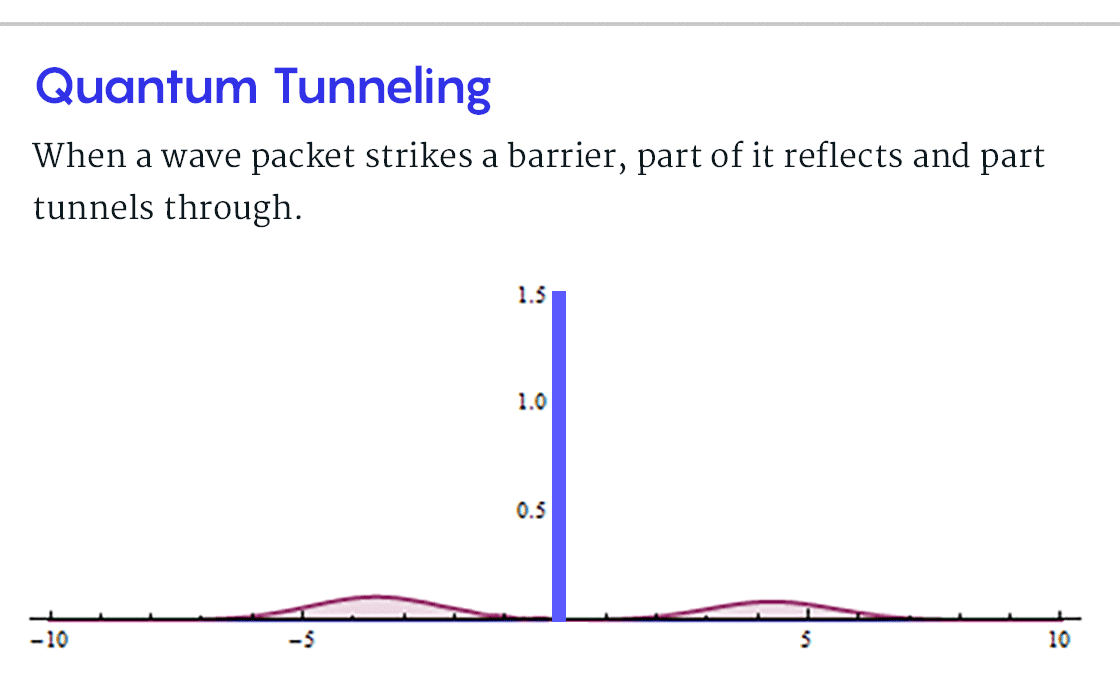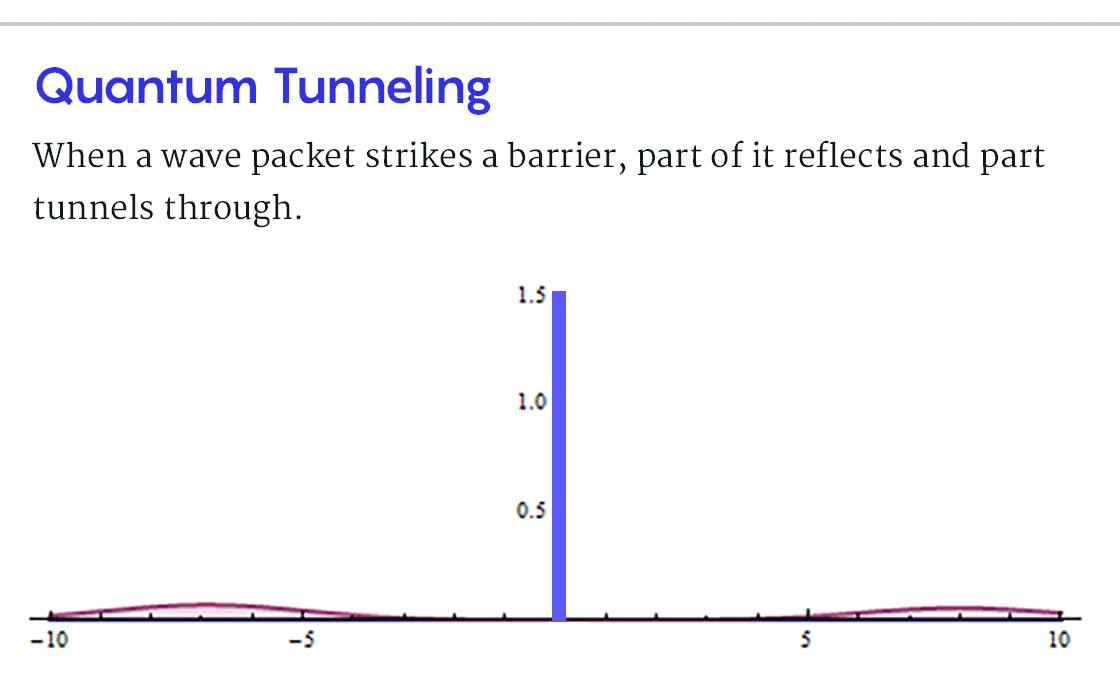
Но, когда частица прибудет в B, что можно будет сказать о ее пути, или о том, как долго она находилась в барьере? Прежде, чем она внезапно появилась B, эта частица представляла собой двухчастную вероятностную волну, одна ее часть была отражена, а вторая просочилась. Волна одновременно преодолела барьер и не преодолела. В таком случае смысл «времени туннелирования» становится неясен.
Но, все-таки, невозможно отрицать, что любая частица, которая вышла из A и оказалась в B, обязательно проходит через барьер, и в какой-то момент взаимодействует с барьером. Вопрос – в какой именно момент?
Стейнберг, который был «подлинно одержим» вопросом о времени туннелирования еще с 1990-х, когда учился в аспирантуре, объясняет, что проблема связана с самой спецификой природы времени. У тел есть определенные характеристики, например, масса или местоположение. Но объекту не присуще некоторое значение «времени», которое можно было бы непосредственно измерить. «Я могу спросить вас: «Где находится мяч?», но не имеет смысла вопрос «В котором часу мяч?»», — говорит Стейнберг, — «время не является свойством, которым обладала бы какая-либо частица». Поэтому время приходится отсчитывать по другим событиям, происходящим в мире, например, по тиканью часов (а ход часов, в конечном итоге, сводится к перемещению стрелок в пространстве). Такие приращения называются «временем».
Но в случае с туннелированием никаких часов внутри частицы не установлено. Как же отслеживать изменения, происходящие с ней? Физики нашли множество «прокси» для туннелирования времени.
Туннелирование и время
Хартман (а до него Лерой Арчибальд Макколл в 1932 году) избрали простейший подход, позволяющий оценить, сколько времени уходит на туннелирование. Хартман рассчитал разницу между временем наиболее вероятного прибытия частицы из точки A в точку B в вакууме по сравнению с аналогичным временем, затрачиваемым, когда частица преодолевает барьер. Для этого он учел, как барьер сдвигает пиковую позицию на колоколообразной кривой передаваемого волнового пакета.
Но с этим подходом есть проблема, и она связана с тем престранным допущением, будто барьер ускоряет частицы. Мы попросту не можем сравнить исходный и конечный пик волнового пакета частицы. Отмеряя на часах разницу между наиболее вероятным временем отправления частицы (когда пик ее колоколообразной кривой находится в точке A) и ее наиболее вероятным временем прибытия (когда пик достигает точки B), мы не узнаем, сколько времени летела конкретная частица, поскольку частица, зафиксированная в B, не обязательно отправилась из A. На момент изначального вероятностного распределения она была везде и нигде, и могла быть, например, в переднем хвосте распределения, который расположен сравнительно близко к барьеру. В таком случае у нее будет шанс быстро достичь B.
Поскольку точные траектории частиц узнать невозможно, исследователи стали искать более вероятностный подход. Рассмотрели тот факт, что, если частица попадает в барьер, то в каждый момент времени существует некоторая вероятность, что частица находится внутри барьера (и вероятность, что она вне барьера). Затем физики суммируют вероятности для каждого мгновения и выводят среднее время туннелирования.
По поводу того, как измерять вероятности, в конце 1960-х были изобретены различные мысленные эксперименты, в которых «часы» можно прикреплять к самим частицам. Если часы каждой частицы «тикают», только пока она находится внутри барьера, и мы снимем показания с часов множества переданных частиц, то у нас получится разброс различных значений времени. Однако, среднее значение будет соответствовать времени туннелирования.
Разумеется, все это проще сказать, чем сделать. «Они просто генерировали безумные идеи о том, как измерить такое время, полагая при этом, что они никогда не воплотятся», — сказал Рамон Рамос, ведущий автор недавней статьи в Nature, — «но наука делает успехи, и мы счастливы, что сегодня такой эксперимент стал реальностью».
Встраиваемые часы
Хотя физики занимались оценкой времени туннелирования с 1980-х, сверхточные измерения стали быстро развиваться сравнительно недавно – в лаборатории Урсулы Келлер в Швейцарской высшей технической школе, Цюрих. Команда Урсулы Келлер смогла измерить время туннелирования при помощи так называемых атточасов. В атточасах Келлер электрон из атома гелия попадает в барьер, который вращается на месте, подобно стрелке часов. Электроны туннелируют чаще всего, когда барьер находится в определенной ориентации – допустим, по атточасам это полдень. Затем, когда электроны появляются из барьера, их отбрасывает в направлении, зависящем от положения барьера в тот момент. Чтобы оценить время туннелирования, команда Келлер измеряла угловую разницу между полуднем, на который приходилось большинство актов туннелирования, и углом, под которым улетали большинство исходящих электронов. Так удалось измерить разницу в 50 аттосекунд, то есть, миллиардных миллиардных долей секунды.
Затем, в работе, о которой было сообщено в 2019 году, группа Литвинюка смогла улучшить эксперимент Келлер с атточасами, взяв вместо гелия более простые атомы водорода. Они измерили даже более краткие промежутки времени, не более двух аттосекунд — это позволяет предположить, что туннелирование происходит почти мгновенно.
Но некоторые эксперты пришли к выводу, что атточасы – не слишком подходящий прибор для измерения времени туннелирования. Манзони, опубликовавший анализ таких измерений, указал, что этот подход ущербен в том же отношении, что и определение времени туннелирования по Хартману. Задним числом можно сказать, что у электронов, практически мгновенно туннелировавших сквозь барьер, была фора.
Тем временем Стейнберг, Рамос и их торонтские коллеги Дэвид Спирингс и Изабель Расико провели эксперимент, оказавшийся более убедительным.
Этот альтернативный подход опирается на факт, что многим частицам присуще магнитное свойство, которое называется «спин». Спин можно сравнить со стрелкой, которая может указывать только вверх или вниз. Но до измерения она может указывать куда угодно. Как открыл в 1897 году ирландский физик Джозеф Лармор, угол спина характеризуется вращением или «прецессией», когда частица находится в магнитном поле. Команда из Торонто смогла уподобить такую прецессию ходу часовых стрелок, и полученное устройство назвали «часами Лармора».
В качестве барьера исследователи воспользовались лазерным лучом и пропустили сквозь него магнитное поле. Затем подготовили атомы рубидия, чьи спины были ориентированы в определенном направлении, и дали этим атомам пройти сквозь барьер. Далее измерили спины атомов, вышедших с другой стороны. Если измерить спин отдельного атома, то всегда получаешь неинформативный результат «вверх» или «вниз». Но, если повторять измерение снова и снова, то совокупные измерения покажут, какую прецессию претерпели спины, пока атомы находились в барьере – следовательно, сколько времени они там провели.
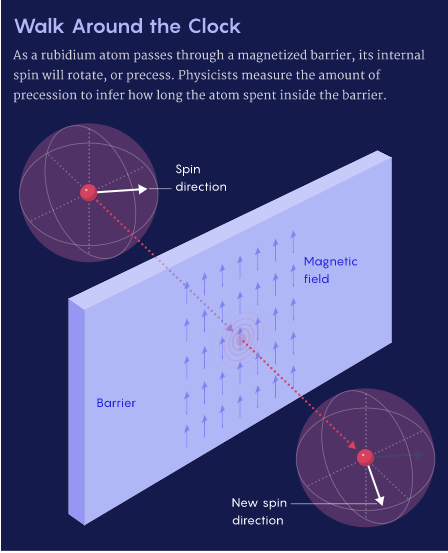
Исследователи сообщили, что атом рубидия остается внутри барьера в среднем на протяжении 0,61 миллисекунд, что согласуется с теми показаниями часов Лармора, что были теоретически спрогнозированы в 1980-е. Чтобы проделать этот путь в вакууме, атомам потребовалось бы больше времени. Следовательно, эти расчеты показывают: если сделать достаточно толстый барьер, то такое ускорение позволит атомам туннелировать сквозь него быстрее скорости света.
Тайна, а не парадокс
В 1907 году Альберт Эйнштейн осознал, что только что сформулированная им теория относительности свидетельствует о невозможности сверхсветовой коммуникации. Представьте себе двоих персонажей, Алису и Боба, которые удаляются друг от друга с большой скоростью. Согласно теории относительности, их часы будут показывать разное время. Поэтому, в частности, если Алиса отправит Бобу сверхсветовой сигнал, а Боб сразу же отправит Алисе сверхсветовой отклик, то ответ Боба может достичь Алису ранее, чем она отправит исходное сообщение. «В таком случае следствие будет предшествовать причине», — писал Эйнштейн.
В целом эксперты сходятся во мнении, что туннелирование не нарушает причинно-следственной связи, но нет однозначного мнения, почему же не нарушает. «Думаю, у нас нет такого представления об этом, которое бы полностью всех устраивало», — говорит Стейнберг, — «это тайна, а не парадокс».
Некоторые убедительные догадки не подтверждаются. Манзони, в начале 2000-х заинтересовавшийся проблемой сверхсветового перемещения при туннелировании, попытался вместе с коллегой переделать вычисления. Они полагали, что увидят снижение скорости туннелирования до субсветовой, если учтут релятивистские эффекты (согласно которым время для быстродвижущихся частиц замедляется). «К нашему удивлению, сверхсветовое туннелирование также оказалось возможным», — сказал Манзони, — «фактически, в релятивистской квантовой механике эта проблема оказалась еще более острой».
Исследователи подчеркивают, что сверхсветовое туннелирование допустимо, коль скоро не допускает сверхсветовой передачи сигналов. По принципу оно похоже на «жуткое дальнодействие», изрядно беспокоившее Эйнштейна. Феномен «жуткого дальнодействия» связан с феноменом квантовой запутанности между сильно удаленными частицами, так, что акт измерения одной частицы мгновенно сказывается на состоянии обеих. Такая мгновенная связь между двумя частицами не вызывает парадоксов, поскольку с ее помощью частицы не могут обмениваться информацией друг с другом.
Правда, учитывая, сколько копий сломано по поводу жуткого дальнодействия, просто удивительно, насколько меньше беспокойства вызывает сверхсветовое туннелирование. «При туннелировании не приходится иметь дела с двумя отдельными системами, состояния которых связаны таким причудливым образом», — говорит Грейс Филд, работающая над проблемой времени туннелирования в Кембриджском университете, — «мы имеем дело всего с одной системой, которая перемещается в пространстве. В таком ключе туннелирование кажется явлением еще более странным, нежели запутанность».
В статье, опубликованной в New Journal of Physics, Поллак и двое его коллег высказываются, что сверхсветовое туннелирование не допускает сверхсветового обмена сигналами по статистическим причинам: пусть даже туннелирование сквозь исключительно толстый барьер происходит очень быстро, крайне низка вероятность, что туннелирование сквозь такой барьер вообще произойдет. Поэтому адресату всегда целесообразнее отправлять сигнал в вакууме.
Почему же не послать тучи частиц сквозь очень-очень толстый барьер, надеясь, что хотя бы одна преодолеет его со сверхсветовой скорости. Не будет ли достаточно всего одной частицы, чтобы передать ваше сообщение и сломать физику? Стейнберг, согласный со статистической трактовкой такой ситуации, настаивает, что единственной туннелировавшей частицы не хватит, чтобы передать информацию. У сигнала должна быть структура и детализация, а любой детализированный сигнал быстрее дойдет до адресата в эфире, нежели через ненадежный барьер.
Поллак считает, что эти вопросы требуют дальнейшего изучения. «Я думаю, что эксперименты Стейнберга подстегнут развитие теории. Куда она нас приведет – не знаю».
Размышления будут сопровождаться новыми экспериментами, у Стейнберга их целый список. Локализуя магнитное поле в разных областях барьера, Стейнберг и его коллеги рассчитывают проверить «не только длительность времени, которое проводит частица внутри барьера, но и где именно она проводит это время». Согласно теоретическим расчетам, большую часть времени атомы рубидия проводят на входе в барьер и на выходе из него, а в середине почти не задерживаются. Рамос отмечает, что «это удивительно и совершенно не поддается объяснению».
Зондируя множество частиц и усредняя, что именно с ними происходит, исследователи все детальнее изображают, что происходит «внутри горы», о чем пионеры квантовой механики даже не могли подумать более века назад. С точки зрения Стейнберга, эти разработки подсказывают: несмотря на все странности, характерные для квантовой механики, «если знать, где в итоге оказалась частица, можно подробнее определить, что с ней происходило до этого».
ссылка на оригинал статьи https://habr.com/ru/post/549122/
Добавить комментарий