Сегодня хочу Вам рассказать одну занимательную историю из юридической практики, когда от теоремы Пифагора буквально зависел достаточно большой срок заключения. В марте 2005 года в Нью-Йорке на пересечении 40-й Западной улицы и 8-й авеню в Манхэттене некто Джеймс Роббинс был задержан за сбыт не самых законных веществ.
Всё бы ничего, но оказалось, что тяжесть преступления увеличивается, ведь торговля проводилась менее, чем в 1000 футах от ближайшей школы – Holy Cross School, находившейся на 43-ей западной улице.
Впрочем, это была позиция обвинения, адвокаты подозреваемого были совсем другого мнения. Взгляните на карту:
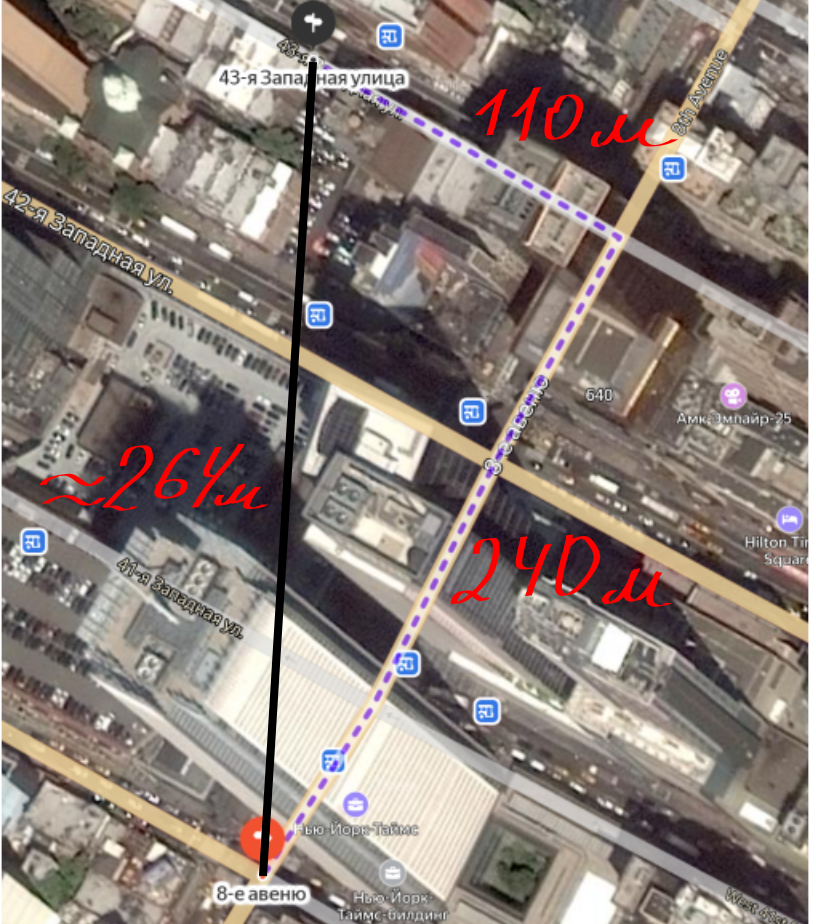
Адвокаты рассуждали так: чтобы непосредственно дойти от места задержания до входа в школу необходимо пройти по 8-й авеню, а затем свернуть на 43-ю западную. Итого по карте примерно 350 метров, что в переводе в буржуйские единицы равняется примерно 1160 футов.
Прокурор же вместе с полицейским департаментом настаивал, что для измерения расстояния необходимо применить теорему Пифагора: в этом случае расстояние по прямой будет равняться чуть менее 900 футов, которые выльются в 5-6 дополнительных лет тюрьмы в связи с отягчающими обстоятельствами.
Интересно, что у американцев выражение «расстояние по прямой» звучит как «as the crow flies» – дословно, «как летит ворона».
Все доводы адвокатов, что расстояние надо измерять по реально возможному маршруту, а «вороны, дескать, наркотики не продают», не были услышаны судом присяжных из 7 человек, и Джеймс Роббинс получил более тяжкую статью.
Это далеко не единственный случай подобного рода споров, но, в целом, американскую судебную практику можно назвать «пифагорейской», потому что такие вопросы всегда трактуются в пользу измерения расстояния по прямой.

А что там про метрические пространства?
Строгая математическая позиция же на этот счет такая: стороны обвинения и защиты просто находились в разных метрических пространствах!
Напомню, что метрическое пространство – это множество точек и заданная на нём особая функция – метрика, определение которой принципиально разрешает нам говорить о расстоянии. Задать метрику – значит написать функцию, которая удовлетворяет трём аксиомам метрики. Определить расстояние – значит вычислить эту функцию для двух точек множества.
В метрическом пространством R², в котором находилась сторона обвинения, метрика задается известной всем со школы функцией:
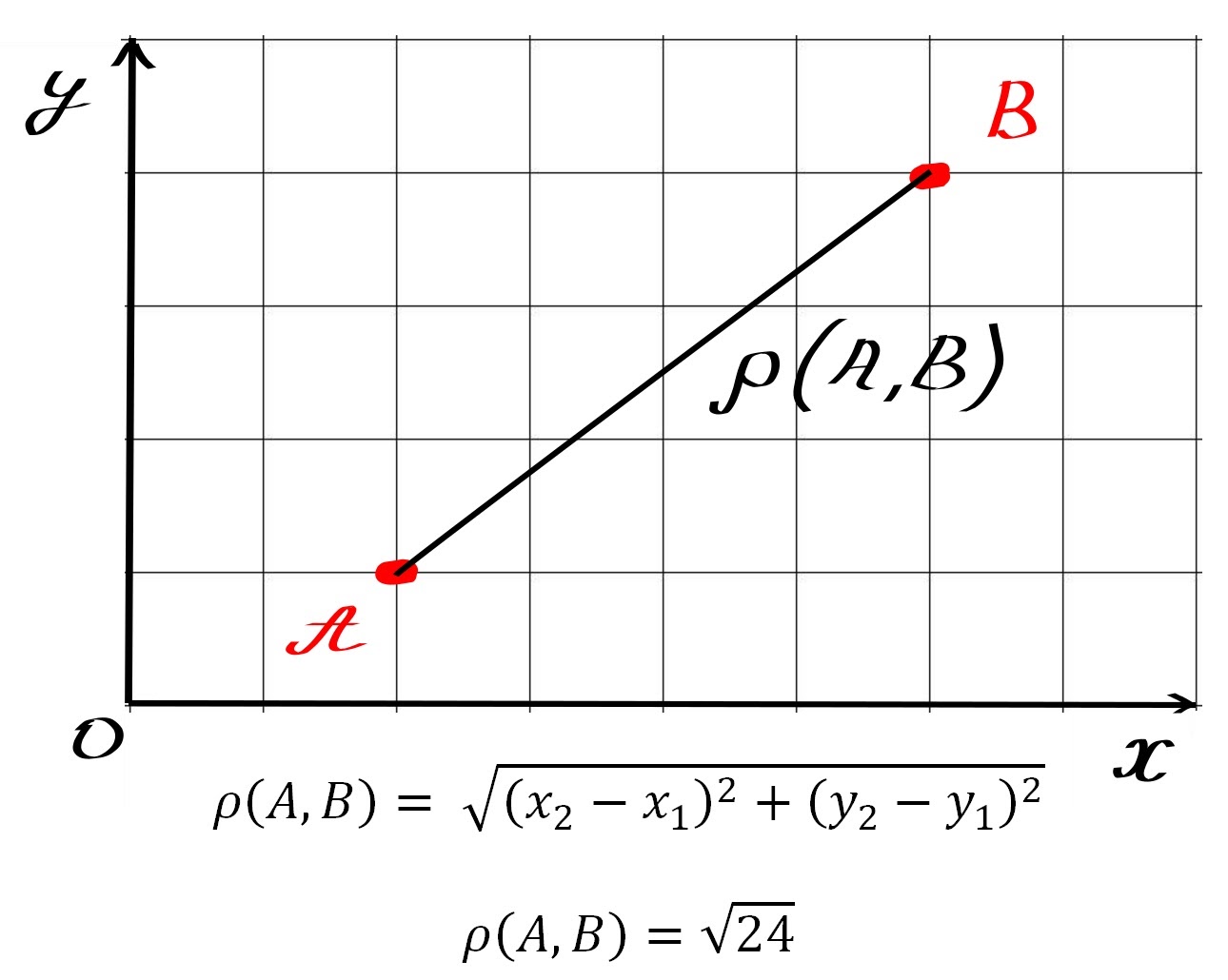
А теперь давайте определим метрику таким образом, как будто мы не можем перемещаться в пустоте между клеток, а только по линиям координатной сетки:
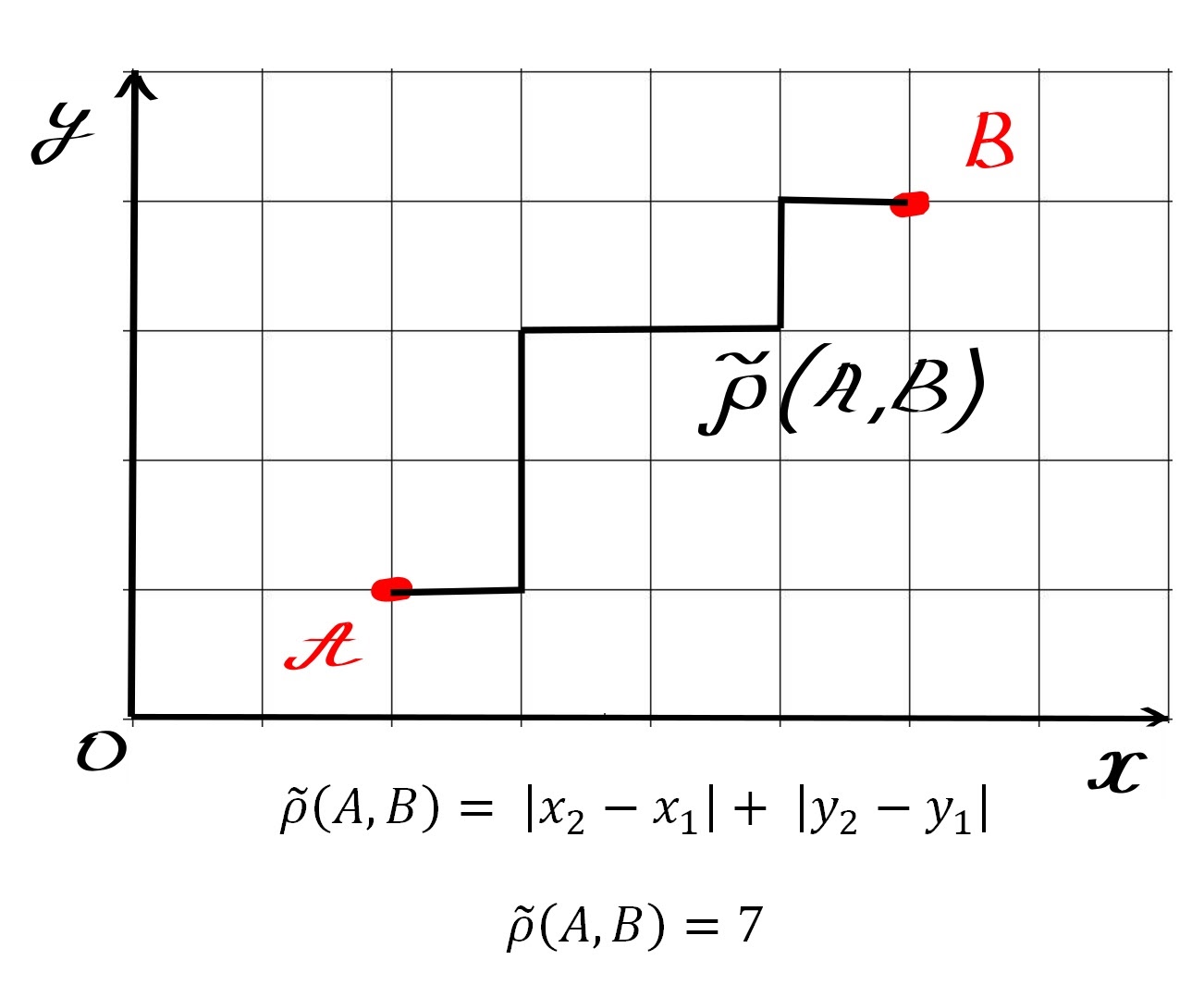
Для такой метрики, как и для привычной нам евклидовой, все аксиомы выполняются. Пространство с такой метрикой называется манхэттеновским, потому что правила игры в нём очень сильно напоминают передвижение по прямоугольной сетке городских кварталов. Находясь в нём, сторона защиты вполне могла рассчитывать на снисхождение, но это был не их день.
Кстати, в качестве заключения. Окружность – это геометрическое место точек. равноудаленных от данной точки, которая называется центром окружности. Число π – отношение длины окружности к диаметру. Смотрим дальше:
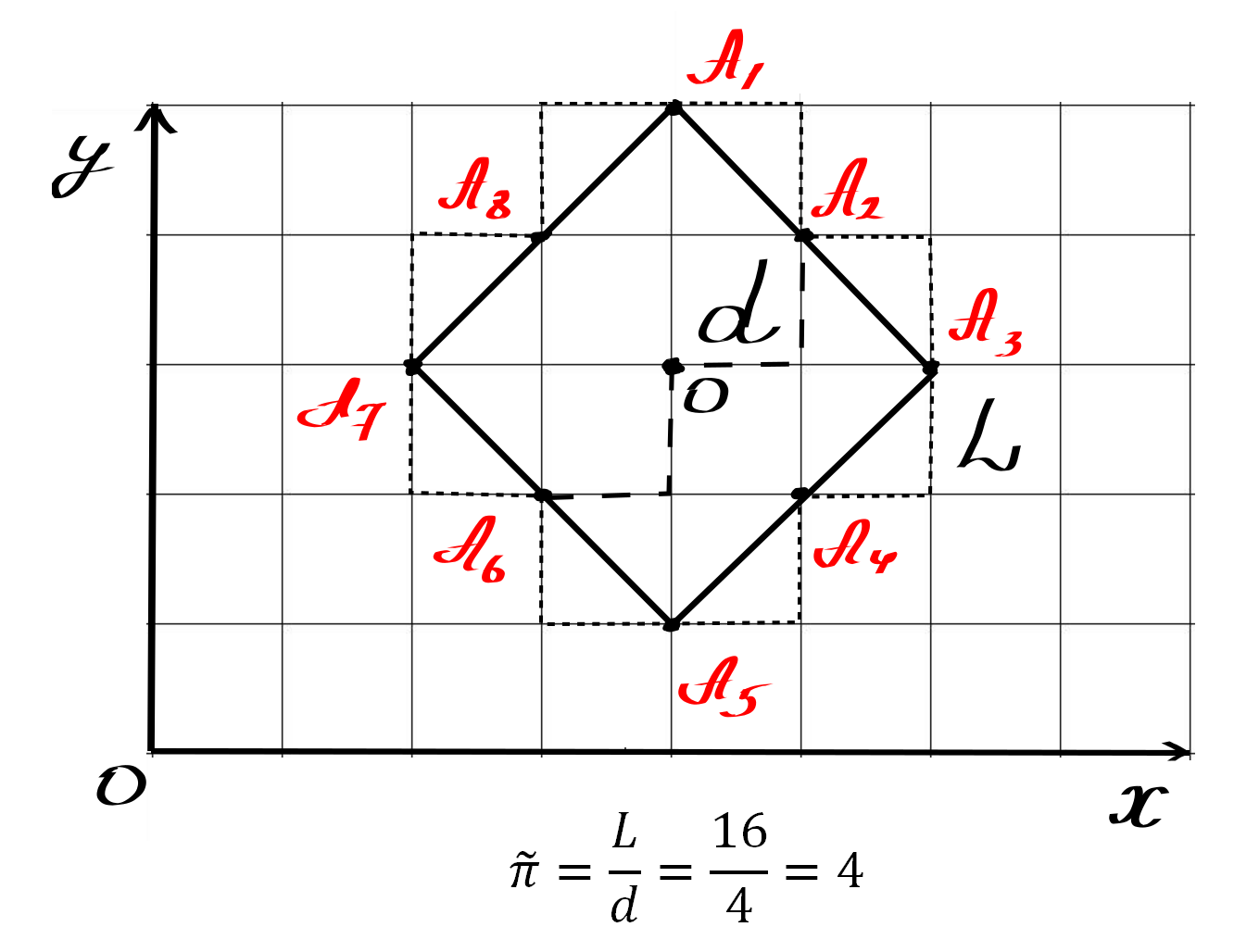
Да, только что я показал Вам, что число π может быть равно 4. Но это ничего не меняет, ведь результат похож на «финт ушами», который так бы хотелось сделать Джеймсу Роббинсу. Не получилось, не фартануло.
(Ссылка на судебный процесс) — дело « Граждане против Джеймса Роббинса»
ссылка на оригинал статьи https://habr.com/ru/company/itsoft/blog/549306/
Добавить комментарий