SavePearlHarbor

Анализ и построение ROC-кривых: связь с РЛС

—

от автора

admin

Постановка задачи

Многие слышали о ROC-кривой, которая часто используется в ML. Расшифровывая данную аббревиатуру мы получаем, что ROC (англ. receiver operating characteristic). При переводе с английского это означает РХП (рабочая характеристика приемника). Данное понятие позаимствовано из теории обнаружения сигналов. ROC-кривую можно связать с радиолокационной станцией (РЛС), рассматривая ее с точки зрения обнаружения объекта. Опишем это более формально.

РЛС посылает импульсы, которые отражаются от объектов. Отражённый сигналXвоспринимается приёмной антенной радара (Рис. 1). Если есть какой-либо объект, находящийся в зоне обнаружения (ЗО)^1 , то отраженный сигнал будет выше порога детектирования\lambdaи это будет означать наличие объекта(D_1). Если отражённый сигнал ниже порога детектирования, то это означает отсутствие объекта(D_0).

Рис. 1 Поясняющий рисунок!
Рис. 1 Поясняющий рисунок!
ЗО

^1Зоной обнаружения РЛС называется область пространства, в пределах которой РЛС обеспечивает обнаружение объектов с вероятностями правильного обнаружения не хуже требуемых.

Наличие объекта обозначим как гипотезаH_1, а его отсутствие как гипотезаH_0. СигналX— это непрерывная случайная величина. Предположим, что мы имеем условные распределения(1), которые нам известны.

\Large f_{(X|H_0)} (x│H_0 ), \ f_{(X|H_1)}(x│H_1)\ \ \ \ (1)

Очевидно, что мы можем говорить о том, чтоXимеет одинаковое распределение для обоих гипотез, но математические ожидания условных распределений(1)будут различными. Так же реалистично предположить, что

\Large E[X│H_0]<E[X│H_1]\ \ \ \ (2)

Учитывая отклонения X, возникающие из-за шума, получаем:

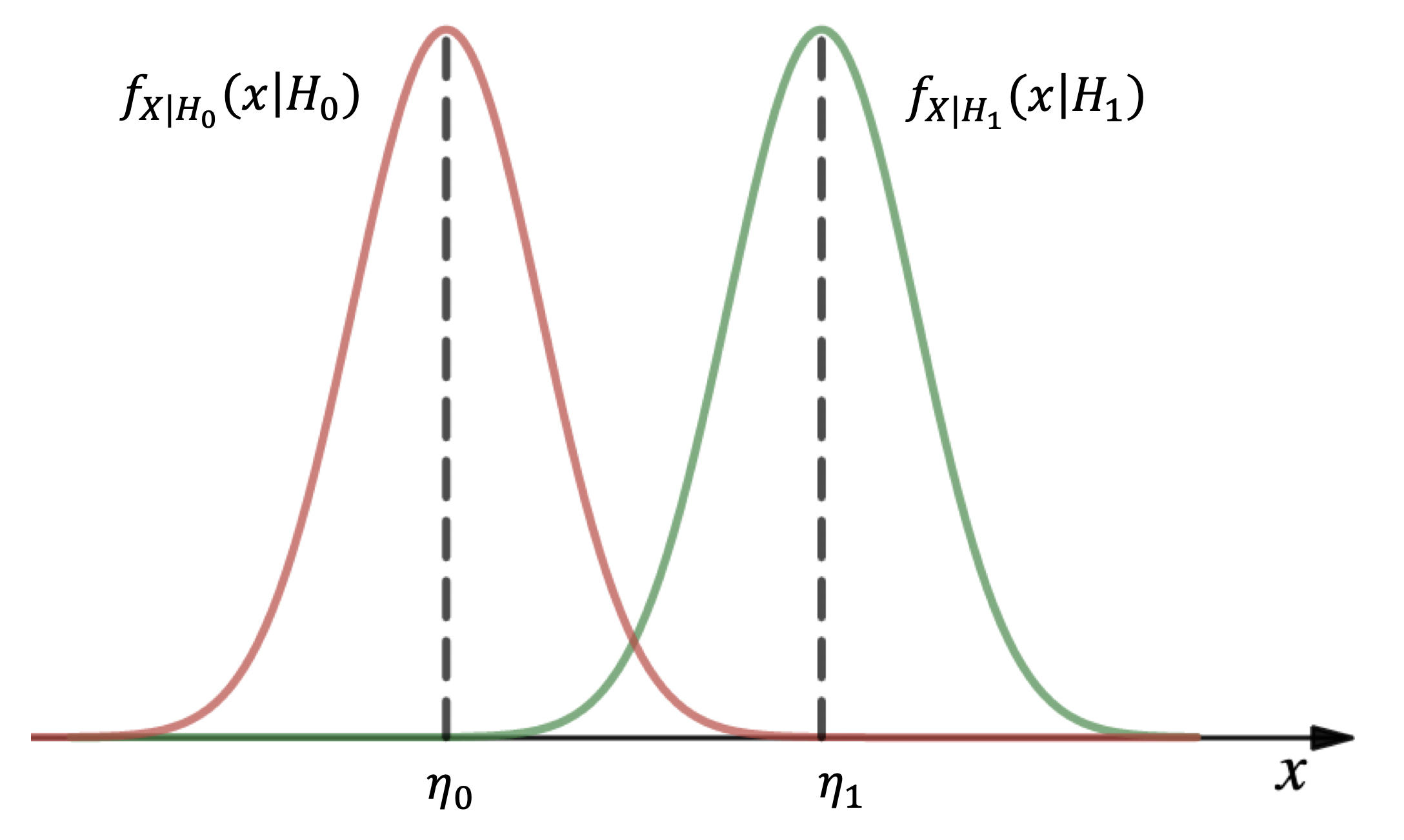
Рис. 2 Условные плотностей (1)
Рис. 2 Условные плотностей (1)

На Рис. 2 \eta_0, \eta_1 — есть условные математические ожидания случайной величиныXпри условии гипотезы H_0иH_1 соответственно. При этом, согласно(2), получаем, что η_0<η_1.

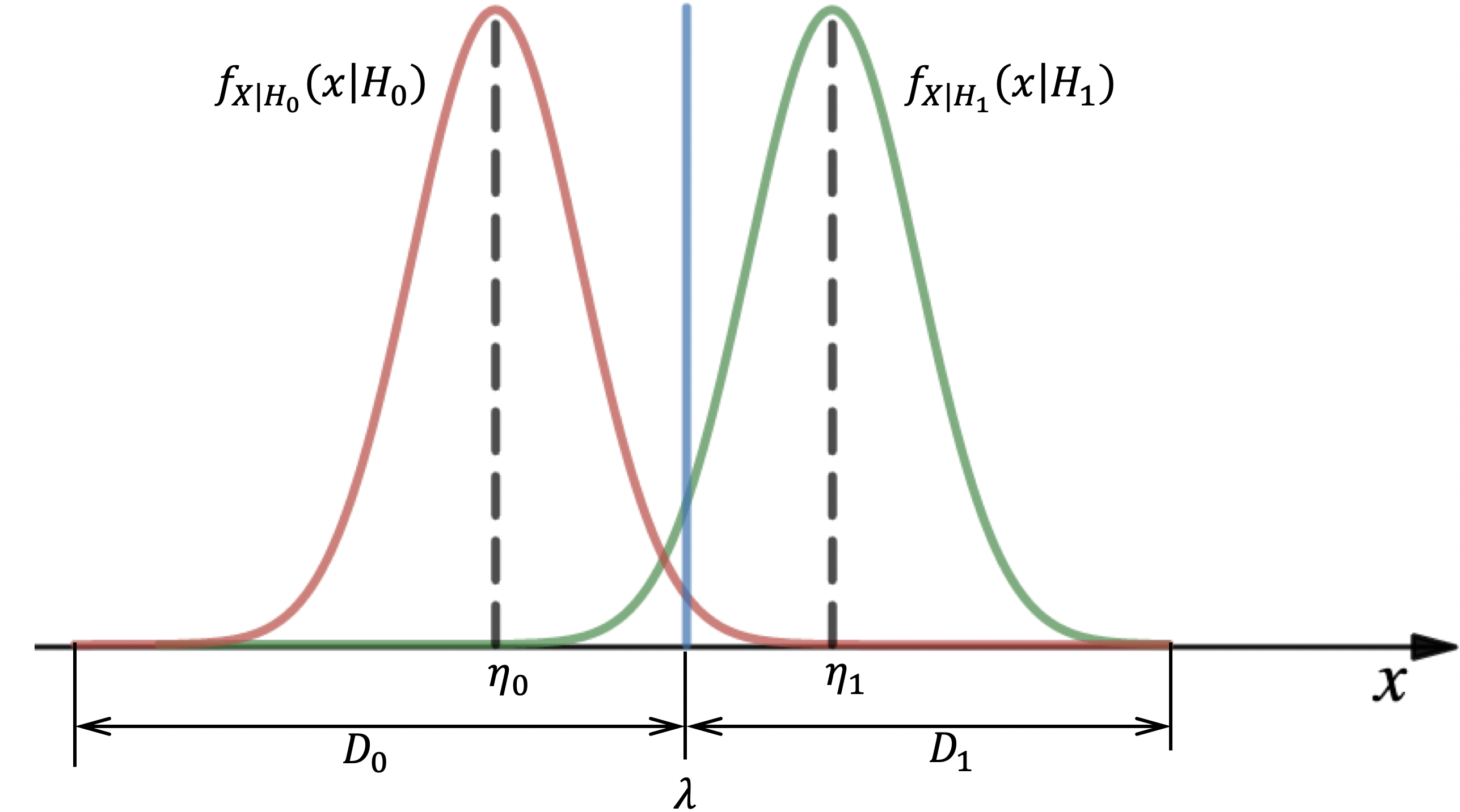
Как уже было сказано ранее, сигнал Xсравнивается с неким порогом, который мы обозначили как λ. Решение о том есть ли объект в ЗО РЛС или нет обозначим как D_1и D_0соответственно. Дополняя Рис. 2 λ, D_1иD_0, получаем:

Рис. 3 Условные распределения плотностей (1) c обозначением уровня порога λ и диапазонов принятия решений D₀ и D₁
Рис. 3 Условные распределения плотностей (1) c обозначением уровня порога λ и диапазонов принятия решений D₀ и D₁

Получаем следующие условные вероятности:

\Large \begin{array}{l} P_{d}=P\left(D_{1} \mid H_{1}\right)=\displaystyle \int_{D_{1}} f_{X \mid H_{1}}\left(x \mid H_{1}\right) d x \\ P_{f a}=P\left(D_{1} \mid H_{0}\right)= \displaystyle \int_{D_{1}} f_{X \mid H_{0}}\left(x \mid H_{0}\right) d x \end{array} (3)

Условные вероятности(3)можно интерпретировать так:

  • P_d– есть вероятность обнаружения объекта при условии, что выполняется гипотеза H_1, т.е. объект действительно находится в ЗО.

  • P_{fa}– есть вероятность ложной тревоги, т.е. мы утверждаем D_1, которое означает принятие решения о наличии объекта в ЗО, когда в действительности выполняетсяH_0, т.е. объекта в ЗО нет.

Визуализируя интегралы (3), получаем:

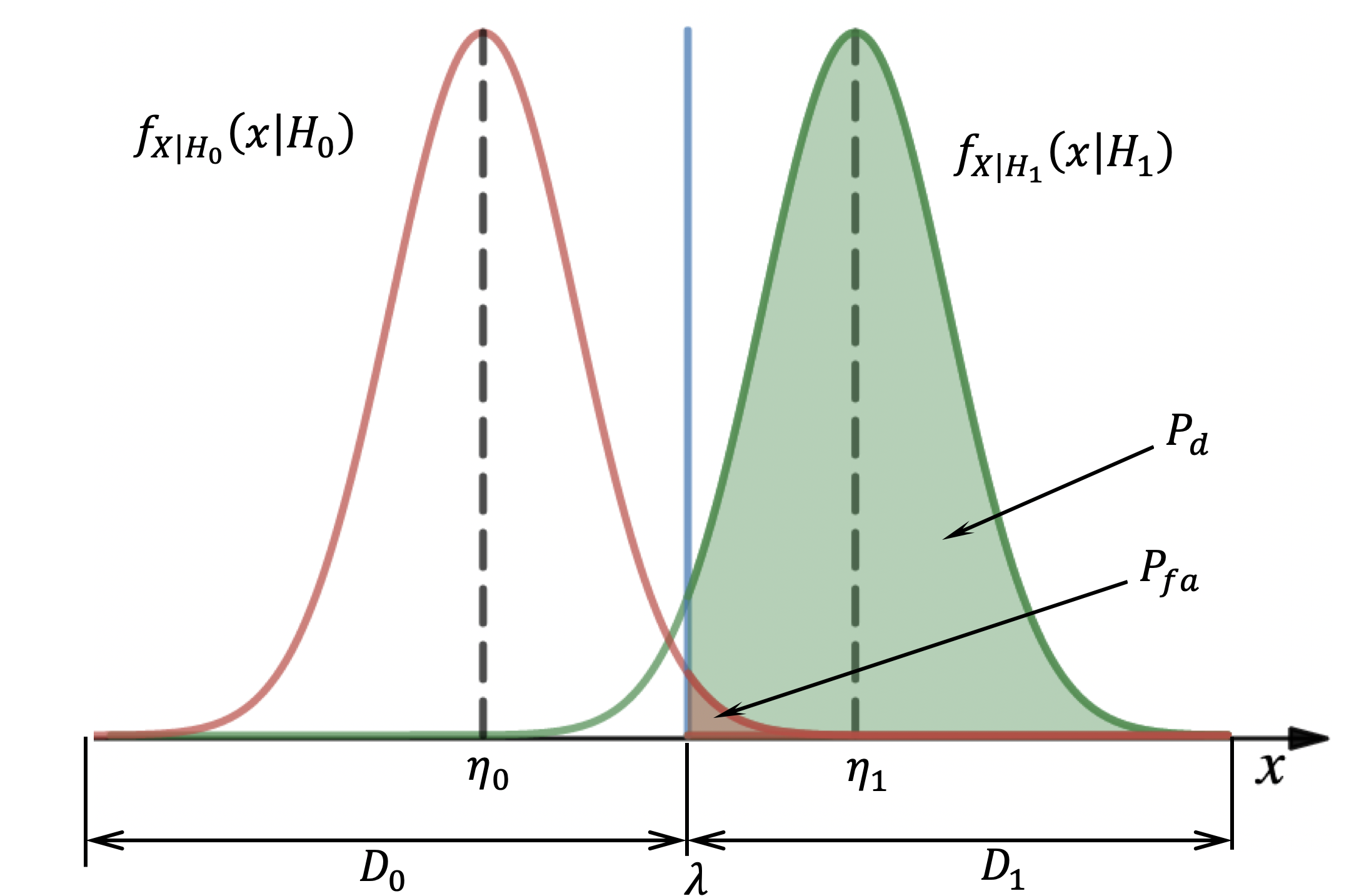
Рис. 4 Вычисление значений P_d и P_fa как площади под кривыми (1)
Рис. 4 Вычисление значений P_d и P_fa как площади под кривыми (1)

Очевидно, что с уменьшением порогаλплощадь под кривыми будет больше, а значит, чтоP_dиP_{fa}будут увеличиваться.

Кривая, показывающая зависимость P_dкак функцию от P_{fa} для различных λ, называется ROC-кривая (англ. Receiver Operating Characteristic, рабочая характеристика приёмника).

Дисперсия случайной величиныXопределяется характеристикой Отношение сигнал-шум (ОТШ, англ. Signal-to-Noise Ratio, сокр. SNR), которая записывается как:

\Large S N R=10 \log _{10}\left(\frac{P_{\text {signal }}}{P_{\text {noise }}}\right)[dB] \ \ \ (4)

  • P_{signal}– мощность сигнала;

  • P_{noise}– мощность шума.

Принимая в (4)P_{signal}=1, а P_{signal}=σ^2– дисперсия, получаем:

\Large S N R=10 \log _{10}\left(\frac{1}{\sigma^{2}}\right)[d B]\ \ (5)

Построение ROC-кривых и их анализ

Пусть заданы следующие начальные условия:

\Large \begin{array}{c} f_{X \mid H_{0}}\left(x \mid H_{0}\right)= \frac{1}{\sqrt{2 \pi \sigma^{2}}} e^{-\frac{x^{2}}{2 \sigma^{2}}} \\ f_{X \mid H_{1}}\left(x \mid H_{1}\right)=\frac{1}{\sqrt{2 \pi \sigma^{2}}} e^{-\frac{(x-1)^{2}}{2 \sigma^{2}}} \end{array} \ \ \ (6)\Large S N R \in[-1,5]\ \ \ (7) \\ \Large \lambda \in[0,1]\ \ \ (8)

Из(6)видно, что мы делаем предположение о том, что условные плотности имеют нормальное распределение, т.е. X \mid H_{0} \sim \mathcal{N}\left(0, \sigma^{2}\right)и X \mid H_{1} \sim \mathcal{N}\left(1, \sigma^{2}\right), где \mathcal{N}\left(\mu, \sigma^{2}\right)– обозначение нормального распределения с математическим ожиданием \muи дисперсией \sigma^{2}. Ранее мы обозначали η_0, η_1как условное математическое ожидание случайной величины X. Исходя из (6), получаем, что η_0= Ε[X│H_0 ]=0, а η_1= Ε[X│H_1 ]=1.

Из диапазона (7)мы можем понять, какой у нас диапазон дисперсии \sigma^2. Для этого выразим из (5)\sigma:

\Large \begin{array}{c} S N R=10 \log _{10}\left(\frac{1}{\sigma^{2}}\right)=10 \log _{10}\left(\sigma^{-2}\right)=-2 \cdot 10 \log _{10} \sigma=-20 \log _{10} \sigma \\ -\frac{S N R}{20}=\log _{10} \sigma \\ \sigma=10^{-\frac{S N R}{20}} \ \ (9) \end{array}

Подставляя граничные точки отрезка из (7), получаем:

\Large \begin{aligned} &\sigma \in\left[\left.10^{-\frac{S N R}{20}}\right|_{S N R=5},\left.10^{-\frac{S N R}{20}}\right|_{S N R=-1}\right]\\ &\sigma \in\left[10^{-\frac{5}{20}}, 10^{-\frac{-1}{20}}\right]\\ &\sigma \in\left[\sqrt[4]{\frac{1}{10}}, \sqrt[20]{10}\right] (10)\end{aligned}

Зададим вектор значений SNR для построения ROC-кривой для каждого из них:

\Large \overrightarrow{{S N R}_{\text {values }}}=(-1,0.5,1,1.5,2,2.5,3,3.5,4,4.5,5)^{T} \text { (11) }

Шаг изменения значений вектора (11)возьмем равным \scriptsize \frac{1}{2}, т.е. \small ∆_{SNR}=\frac{1}{2}. Определим теперь ROC-кривую как параметрическую функцию P_dот P_{fa}, где в качестве параметра выступает λ∈[0,1]. Из (3)и (6), получаем:

\Large \text { ROC }_{\text {curve }}(\sigma, \lambda)=\left\{ \begin{array}{r} P_{f a}= \displaystyle\frac{1}{\sqrt{2 \pi \sigma^{2}}} \displaystyle \int_{\lambda}^{+\infty} e^{-\frac{x^{2}}{2 \sigma^{2}}} d x \\ P_{d}= \displaystyle\frac{1}{\sqrt{2 \pi \sigma^{2}}} \displaystyle \int_{\lambda}^{+\infty} e^{-\frac{(x-1)^{2}}{2 \sigma^{2}}} d x \end{array} \right. (12)

\sigma– задает конкретную ROC-кривую из семейства ROC-кривых.

Зададим теперь вектор значений λ:

\Large \overrightarrow{\lambda_{\text {values }}}=(0,0.01,0.02, \ldots, 0.98,0.99,1)^{T} (13)

Шаг изменения значений вектора (13)возьмем равным \small \frac{1}{100} , т.е. \small ∆_λ=\frac{1}{100}. Вектор (13)содержит 101значение, т.е. имеем 101точку для каждого графика. Таким образом, графики будут визуально выглядеть гладкими.

Имеющихся данных достаточно для построения ROC-кривых.

Воспользуемся для этого языком Python.

Подключение библиотек 
# подключение дополнительных библиотек from scipy.stats import norm from scipy.misc import derivative import numpy as np import pandas as pd  import matplotlib.pyplot as plt import seaborn as sns; sns.set() %matplotlib inline
Дополнительные функции и начальные условия 
# зададим вектор SNR и lambda SNR_values = np.arange(-1, 5.5, 1/2)  lambda_values = np.arange(0, 1.01, 1/100)   # функция, которая возвращает значение sigma по заданному значению SNR def snr_to_sigma(SNR):     return np.power(10, -SNR/20)    # функция, которая возвращает значения Pfa и Pd по заданным sigma и lambda def roc_curve(sigma, lambda_):     return 1 - norm.cdf(lambda_/sigma), 1 - norm.cdf((lambda_ - 1)/sigma)  # создание DataFrame в котором будут храниться значения Pfa, Pd, SNR data = [] for SNR in SNR_values:     for lambda_ in lambda_values:         Pfa, Pd = roc_curve(snr_to_sigma(SNR), lambda_)         data.append([Pfa, Pd, str(SNR)])          data = pd.DataFrame(data, columns=['Pfa', 'Pd', 'SNR'])
Код для построения графика 
fig, ax = plt.subplots(figsize=(18, 14)) sns.set_context('poster') plt.title('$ROC$-кривые в зависимости от значения $SNR$', fontsize=40) plt.xlabel('$P_{fa}$', fontsize=40) plt.xticks(np.arange(0, 0.7, 0.05), fontsize=30) plt.yticks(np.arange(0.5, 1, 0.05), fontsize=30) plt.ylabel('$P_d$', fontsize=40, rotation=0, labelpad=40) sns.lineplot(x='Pfa', y='Pd', hue='SNR',               data=data, palette='gist_ncar', ax=ax)  ax.annotate("Возрастание $\lambda$", xy=(0.15, 0.81),  xycoords='data',             xytext=(90, 150), textcoords='offset points',             size=30, ha='left',              arrowprops=dict(arrowstyle="->", color='black',                             connectionstyle="arc3,rad=0.1")) plt.grid(color='black', linestyle='--', linewidth=1, alpha=0.3)  plt.legend(fontsize='small', shadow=True, title='$SNR(dB)$',            borderpad=0.9, fancybox=True);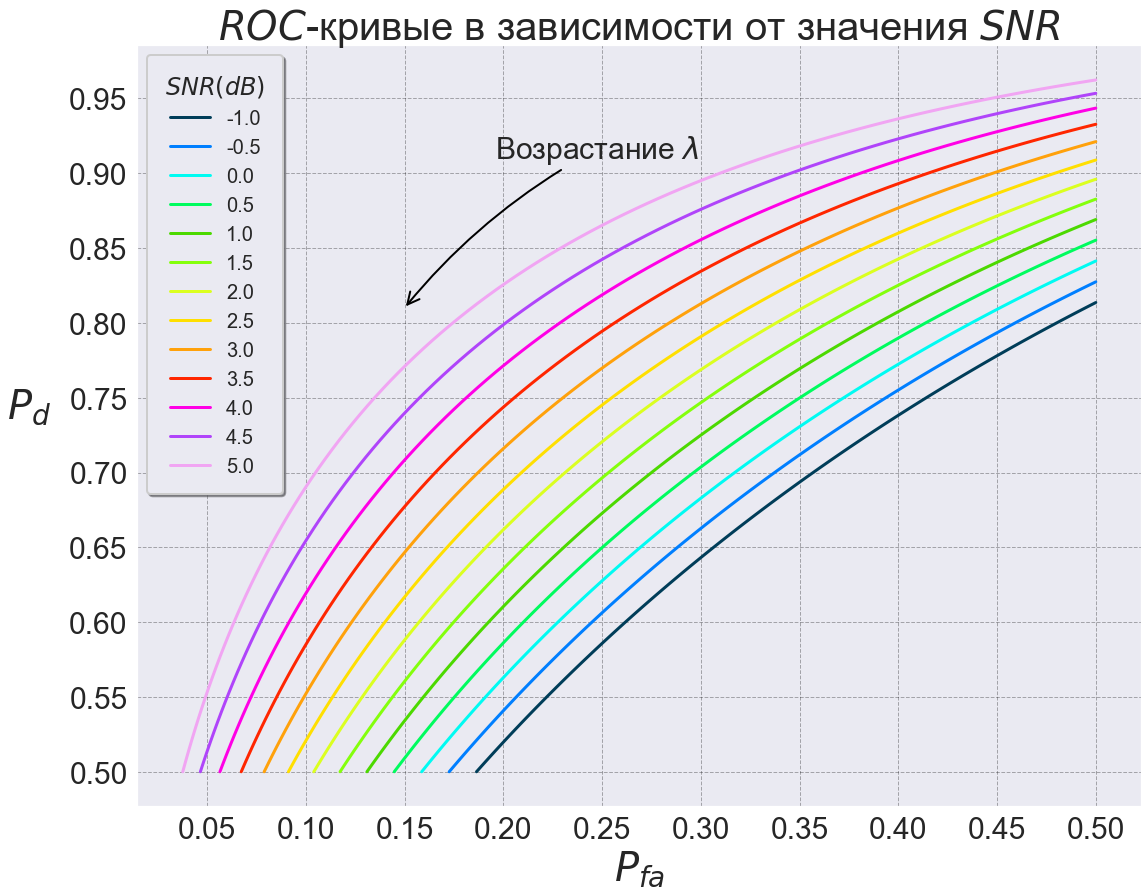
Рис. 5 ROC-кривые в зависимости от значения SNR
Рис. 5 ROC-кривые в зависимости от значения SNR

Из графика видно следующее:

  1. Все кривые начинают свое движение с линии P_{fa}=0.5и заканчивают на линии P_d=0.5;

  2. Чем больше значение SNR, тем ближе ROC-кривая к точке (0,1);

  3. Все кривые выпуклы вверх;

  4. ROC — кривая монотонно не убывает. Чем выше лежит кривая, тем лучше качество РЛС.

Первое объясняется ограниченностью значения порога детектирования (8). Посмотрим, как будут выглядеть ROC-кривые, если увеличить диапазон λ, например, до [-10,10].

Дополнительный код 
# создание DataFrame в котором будут храниться значения Pfa, Pd, SNR data2 = [] for SNR in SNR_values:     for lambda_ in np.arange(-10, 10.1, 1/10) :         Pfa, Pd = roc_curve(snr_to_sigma(SNR), lambda_)         data2.append([Pfa, Pd, str(SNR)])          data2 = pd.DataFrame(data2, columns=['Pfa', 'Pd', 'SNR'])
Код для построения графика 
fig, ax = plt.subplots(figsize=(18, 14)) sns.set_context('poster') plt.title('$ROC$-кривые в зависимости от значения $SNR$', fontsize=40) plt.xlabel('$P_{fa}$', fontsize=40) plt.xticks(np.arange(0, 1.05, 0.1), fontsize=20) plt.yticks(np.arange(0, 1.05, 0.1), fontsize=20) plt.ylabel('$P_d$', fontsize=40, rotation=0, labelpad=40) sns.lineplot(x='Pfa', y='Pd', hue='SNR',               data=data2, palette='gist_ncar', ax=ax)  ax.annotate("Возрастание $\lambda$", xy=(0.15, 0.81),  xycoords='data',             xytext=(90, 110), textcoords='offset points',             size=20, ha='left',              arrowprops=dict(arrowstyle="->", color='black',                             connectionstyle="arc3,rad=0.1")) plt.grid(color='black', linestyle='--', linewidth=1, alpha=0.3)  plt.legend(fontsize='small', shadow=True, title='$SNR(dB)$',            borderpad=0.9, fancybox=True);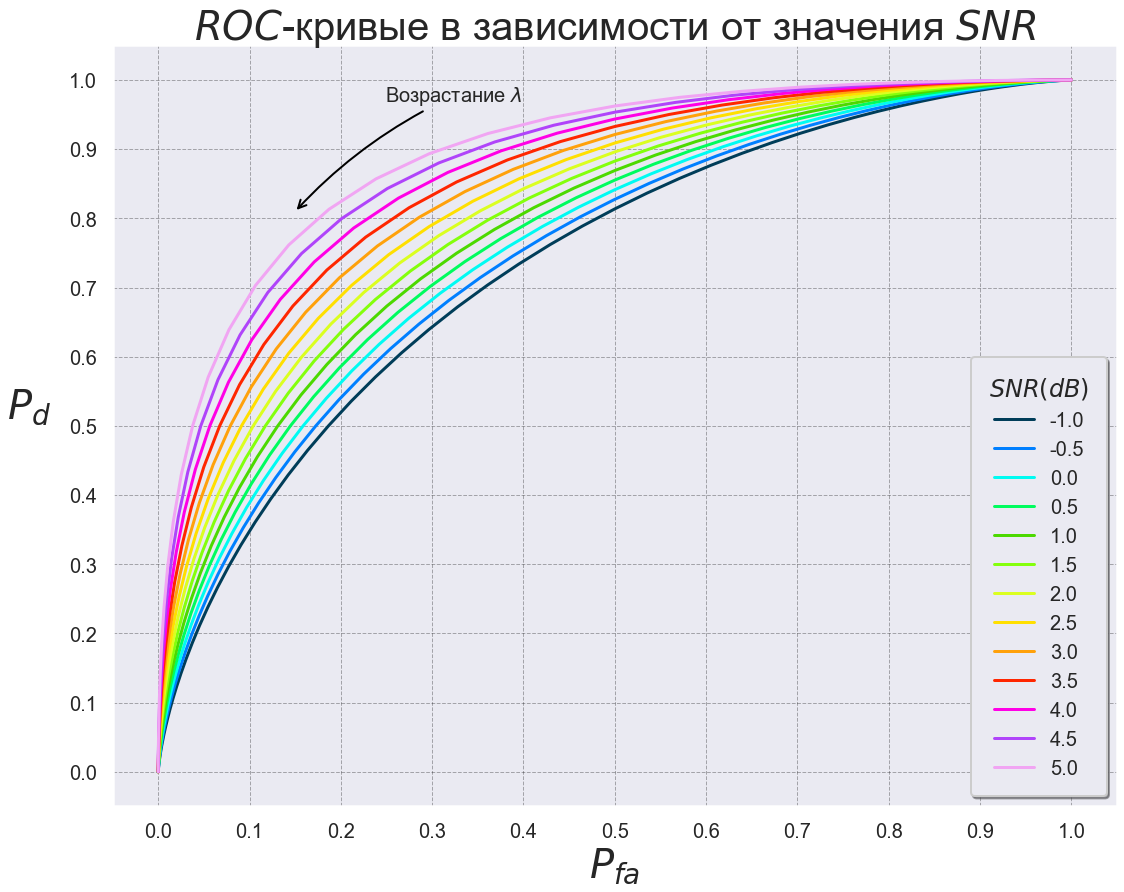
Рис. 6 ROC-кривые в зависимости от значения SNR c увеличенным диапазоном λ.
Рис. 6 ROC-кривые в зависимости от значения SNR c увеличенным диапазоном λ.

Второе объясняется тем, что можно достичь большего значения P_dпри меньшем значении P_{fa}. Это происходит потому, что при увеличении значения SNR, уменьшается значение σ, что видно из (9). Посмотрим, как визуально изменяются кривые условных плотностей (6)при разных значениях SNR.

Дополнительный код 
# функция, которая возвращает значение условных плотностей в зависимости от sigma  def conditional_density(x, sigma):     return norm.pdf(x/sigma), norm.pdf((x - 1)/sigma)          # создание DataFrame в котором будут храниться значения условных плотностей и SNR data3 = [] x_range = np.linspace(-5, 5, 100) for SNR in SNR_values:     for x in x_range :         cond_dens1, cond_dens2 = conditional_density(x, snr_to_sigma(SNR))         data3.append([cond_dens1, cond_dens2, str(SNR), x])          data3 = pd.DataFrame(data3, columns=['cond_dens1', 'cond_dens2', 'SNR', 'x'])
Код для построения графика 
fig, ax = plt.subplots(figsize=(20, 10)) sns.set_context('poster') plt.title('Условные распределения в зависимости от значения $SNR$',            fontsize=30) plt.xlabel('$x$', fontsize=40) plt.xticks(np.arange(-5, 5.5, 0.5), fontsize=20) plt.yticks(np.arange(0, 0.45, 0.05), fontsize=20) plt.ylabel('Значение условной плотности', fontsize=20,             labelpad=30)  sns.lineplot(x='x', y='cond_dens2', hue='SNR',               data=data3, palette='gist_ncar', ax=ax)  sns.lineplot(x='x', y='cond_dens1', hue='SNR',               data=data3, palette='gist_ncar', ax=ax, legend=False)  ax.legend(fontsize='small', shadow=True, title='$SNR(dB)$',            borderpad=0.9, fancybox=True, loc='upper left')  ax.annotate("$f_{X|H_0}(x|H_0)$", xy=(-0.6, 0.35),  xycoords='data',             xytext=(-90, 20), textcoords='offset points',             size=30, ha='right',              arrowprops=dict(arrowstyle="->", color='black',                             connectionstyle="arc3,rad=0.1"))  ax.annotate("$f_{X|H_1}(x|H_1)$", xy=(1.6, 0.35),  xycoords='data',             xytext=(100, 20), textcoords='offset points',             size=30, ha='left',              arrowprops=dict(arrowstyle="->", color='black',                             connectionstyle="arc3,rad=0.1"))  plt.grid(color='black', linestyle='--', linewidth=1, alpha=0.3);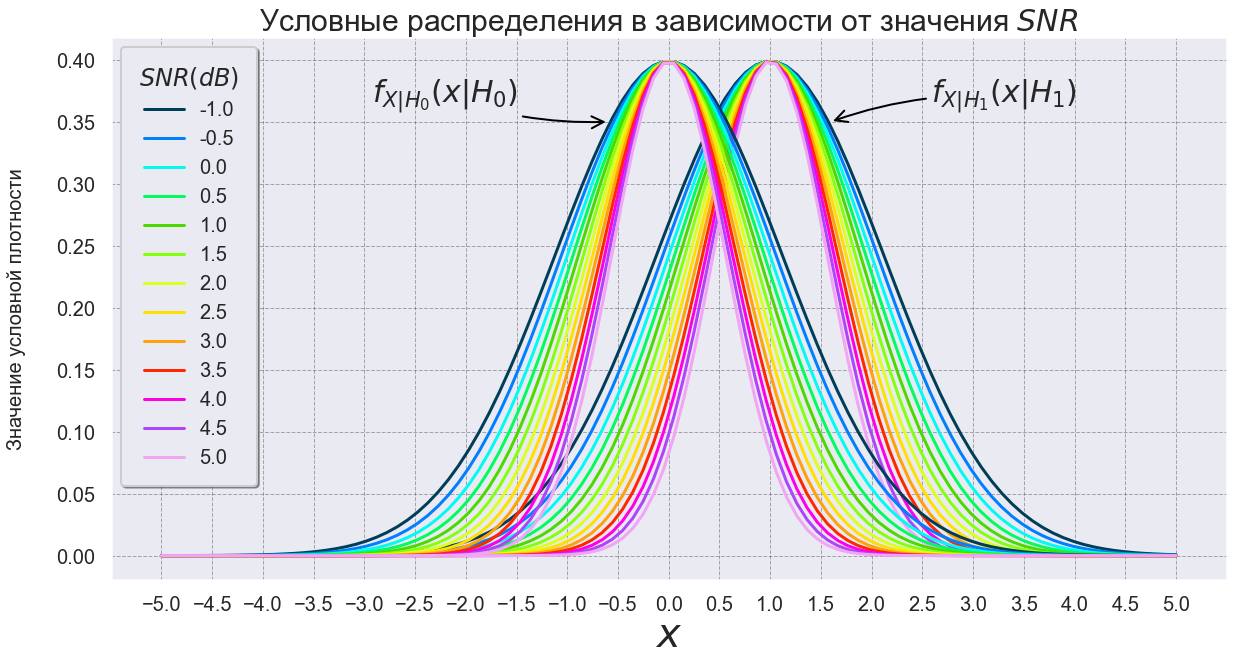
Рис. 7 Условные распределения (6) в зависимости от SNR
Рис. 7 Условные распределения (6) в зависимости от SNR

По Рис. 7 видно, что при увеличении SNR, кривые становятся уже, а, значит, пересекаются в меньшей степени. Посмотрим теперь на зависимость вероятности обнаружения P_dот λ:

Дополнительный код 
data4 = [] for SNR in SNR_values:     for lambda_ in lambda_values:         Pfa, Pd = roc_curve(snr_to_sigma(SNR), lambda_)         data4.append([Pfa, Pd, str(SNR), lambda_])          data4 = pd.DataFrame(data4, columns=['Pfa', 'Pd', 'SNR', 'lambda'])
Код для построения графика 
fig, ax = plt.subplots(figsize=(16, 12)) sns.set_context('poster') plt.title('Кривые $P_d$ от $\lambda$ при разных $SNR$', fontsize=40) plt.xlabel('$\lambda$', fontsize=40) plt.xticks(np.arange(0, 1.05, 0.1), fontsize=20) plt.yticks(np.arange(0.5, 1.05, 0.1), fontsize=20) plt.ylabel('$P_d$', fontsize=40, rotation=0, labelpad=40) sns.lineplot(x='lambda', y='Pd', hue='SNR',               data=data4, palette='gist_ncar', ax=ax)  ax.annotate("Возрастание $\lambda$", xy=(0.5, 0.85),  xycoords='data',             xytext=(-10, 50), textcoords='offset points',             size=20, ha='right',              arrowprops=dict(arrowstyle="->", color='black',                             connectionstyle="arc3,rad=-0.2")) plt.grid(color='black', linestyle='--', linewidth=1, alpha=0.3)  plt.legend(fontsize='small', shadow=True, title='$SNR(dB)$',            borderpad=0.9, fancybox=True);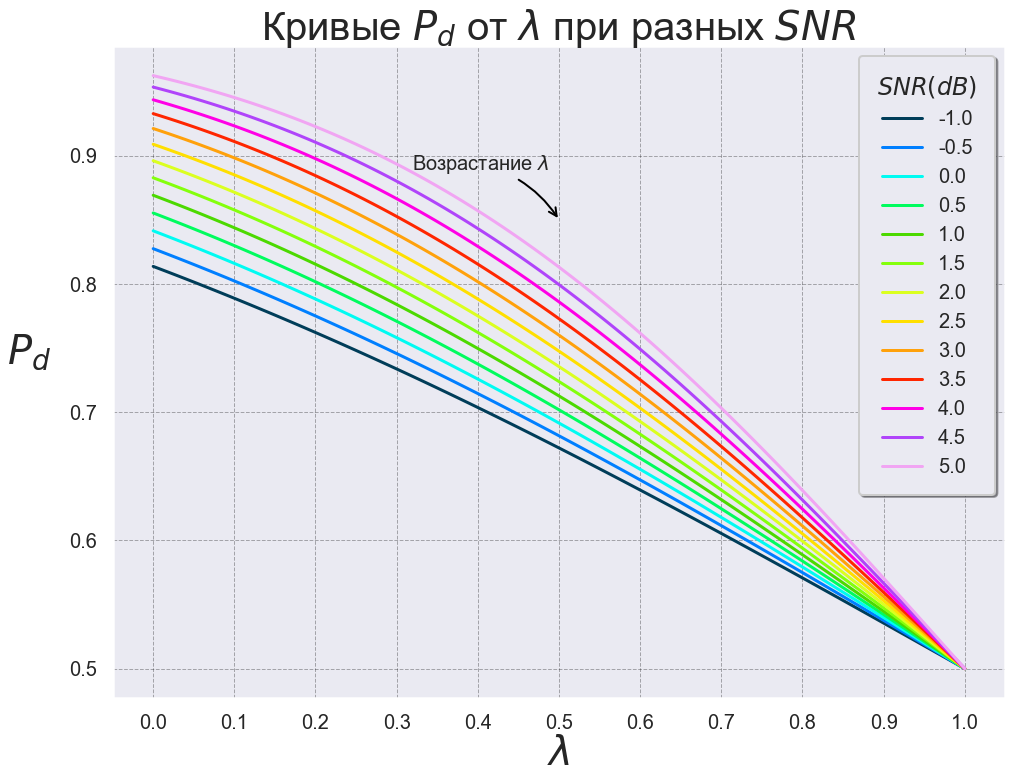
Рис. 8 Кривые зависимости P_d от λ при различных значениях SNR
Рис. 8 Кривые зависимости P_d от λ при различных значениях SNR

P_d достигает максимального значения при λ=0и SNR=5. Но при таком низком пороге детектирования мы получаем:

Код для построения графика 
fig, ax = plt.subplots(figsize=(16, 12)) sns.set_context('poster') plt.title('Кривые $P_{fa}$ от $\lambda$ при разных $SNR$', fontsize=40) plt.xlabel('$\lambda$', fontsize=40) plt.ylabel('$P_{fa}$', fontsize=40, rotation=0, labelpad=40) sns.lineplot(x='lambda', y='Pfa', hue='SNR',               data=data4, palette='gist_ncar', ax=ax)  ax.annotate("Возрастание $\lambda$", xy=(0.5, 0.35),  xycoords='data',             xytext=(-10, 90), textcoords='offset points',             size=30, ha='right',              arrowprops=dict(arrowstyle="->", color='black',                             connectionstyle="arc3,rad=0.2")) plt.grid(color='black', linestyle='--', linewidth=1, alpha=0.3)  plt.legend(fontsize='small', shadow=True, title='$SNR(dB)$',            borderpad=0.9, fancybox=True);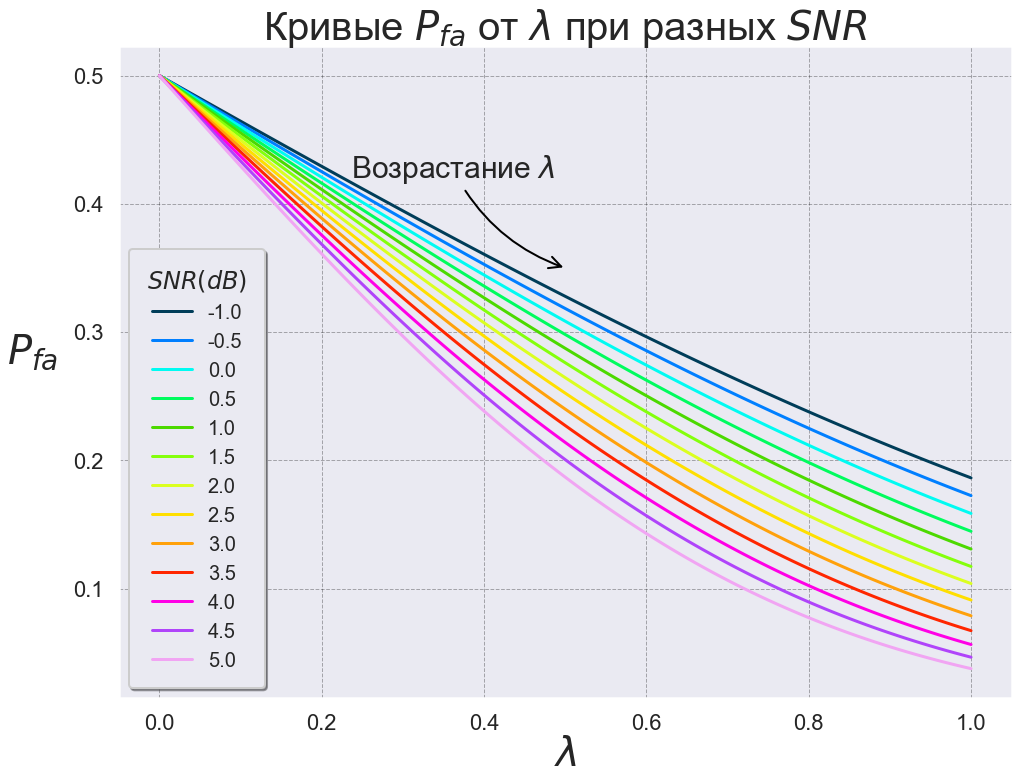
Рис. 9 Кривые зависимости P_{fa} от λ при различных значениях SNR.
Рис. 9 Кривые зависимости P_{fa} от λ при различных значениях SNR.

При λ=0получается, что вероятность ложной тревоги равна \small \frac{1}{2}, так как определенный интеграл от условной плотности распределения

\large \left.\frac{1}{\sqrt{2 \pi \sigma^{2}}} \int_{\lambda}^{+\infty} e^{-\frac{x^{2}}{2 \sigma^{2}}} d x\right|_{\lambda=\eta_{0}}

считается от значения математического ожидания до +∞, что в точности равно \small \frac{1}{2}, в силу симметричности плотности нормального распределения.

Третье объясняется тем, что тангенс угла наклона ROC-кривой в некоторой ее точке равен значению плотностей (6)от порога детектирования λ, необходимому для достижения P_dи P_{fa} в этой точке.

Пусть

\Large \tan \left(\alpha_{\lambda}\right):=\frac{\left(\frac{d P_{d}}{d \lambda}\right)}{\left(\frac{d P_{f a}}{d \lambda}\right)} \ \ ,(14)

тогда:

\Large \begin{aligned} &\tan \left(\alpha_{\lambda}\right)= \frac{\frac{d}{d \lambda}\left(\frac{1}{\sqrt{2 \pi \sigma^{2}}} \displaystyle \int_{\lambda}^{+\infty} e^{-\frac{(x-1)^{2}}{2 \sigma^{2}}} d x\right)}{\frac{d}{d \lambda}\left(\frac{1}{\sqrt{2 \pi \sigma^{2}}} \displaystyle \int_{\lambda}^{+\infty} e^{-\frac{x^{2}}{2 \sigma^{2}}} d x\right)}=\frac{-\frac{1}{\sqrt{2 \pi \sigma^{2}}} e^{-\frac{(\lambda-1)^{2}}{2 \sigma^{2}}}}{-\frac{1}{\sqrt{2 \pi \sigma^{2}}} e^{-\frac{(\lambda)^{2}}{2 \sigma^{2}}}}=\\ &=\frac{e^{-\frac{(\lambda-1)^{2}}{2 \sigma^{2}}}}{e^{-\frac{(\lambda)^{2}}{2 \sigma^{2}}}}=e^{-\frac{(\lambda-1)^{2}}{2 \sigma^{2}}+\frac{(\lambda)^{2}}{2 \sigma^{2}}}=e^{\frac{-\lambda^{2}+2 \lambda-1+\lambda^{2}}{2 \sigma^{2}}}=e^{\frac{2 \lambda-1}{2 \sigma^{2}}} \ \ \ (15) \end{aligned}

Исследуем функцию (15):

\Large \begin{array}{l} \displaystyle \lim _{\lambda \rightarrow-\infty}\left(\tan \left(\alpha_{\lambda}\right)\right)=\lim _{\lambda \rightarrow-\infty}\left(e^{\frac{2 \lambda-1}{2 \sigma^{2}}}\right)=0 \\ \displaystyle \lim _{\lambda \rightarrow+\infty}\left(\tan \left(\alpha_{\lambda}\right)\right)= \lim _{\lambda \rightarrow+\infty}\left(e^{\frac{2 \lambda-1}{2 \sigma^{2}}}\right)=+\infty \end{array} (16)

Из (15) и (16)следует, что тангенс угла наклона ROC-кривой монотонно изменяется от 0до +∞при λот -∞до +∞. Таким образом, начиная построение графика от λ=-∞ \ tan⁡(α_λ )=0и, следовательно, α_λ=0°. Заканчивается все в точке λ=+∞, когда tan⁡(α_λ )=+∞, т.е. α_λ=90°(касательная в данной точке перпендикулярна оси абсцисс).

Дополнительный код 
# функция, которая возвращает значения Pfa и Pd по заданным sigma и lambda def dif_roc_curve(sigma, lambda_):     return (derivative(lambda x: 1 - norm.cdf(x/sigma), lambda_, dx=1e-10),            derivative(lambda x: 1 - norm.cdf((x - 1)/sigma), lambda_, dx=1e-10))   data5 = [] for SNR in SNR_values:     for lambda_ in [0, 0.5, 1]:         dPfa, dPd = dif_roc_curve(snr_to_sigma(SNR), lambda_)         Pfa, Pd = roc_curve(snr_to_sigma(SNR), lambda_)         tan = dPd/dPfa         for i in np.arange(0.01/tan, 0.2/tan, 0.01/tan):             data5.append([tan*(i - Pfa) + Pd, i, str(SNR), lambda_])          data5 = pd.DataFrame(data5, columns=['y', 'x', 'SNR', 'lambda'])
Код для построения графика 
fig, ax = plt.subplots(figsize=(18, 14)) sns.set_context('poster') plt.title('$ROC$-кривая с $3^{мя}$ касательными', fontsize=40) plt.xlabel('$P_{fa}$', fontsize=40) plt.xticks(np.arange(0, 1.05, 0.1), fontsize=20) plt.yticks(np.arange(0, 1.05, 0.1), fontsize=20) plt.ylabel('$P_d$', fontsize=40, rotation=0, labelpad=40) sns.lineplot(x='Pfa', y='Pd', hue='SNR', legend=False,              data=data[data['SNR']  == '5.0'], palette='gist_ncar', ax=ax) sns.lineplot(x='x', y='y', hue='lambda', linestyle='--',              data=data5[data5['SNR']  == '5.0'],               palette='dark:b', legend=True,  ax=ax)  plt.grid(color='black', linestyle='--', linewidth=1, alpha=0.3)  plt.legend(fontsize='small', shadow=True, title='Касательная для $\lambda=$',            borderpad=0.9, fancybox=True, loc=4);

/

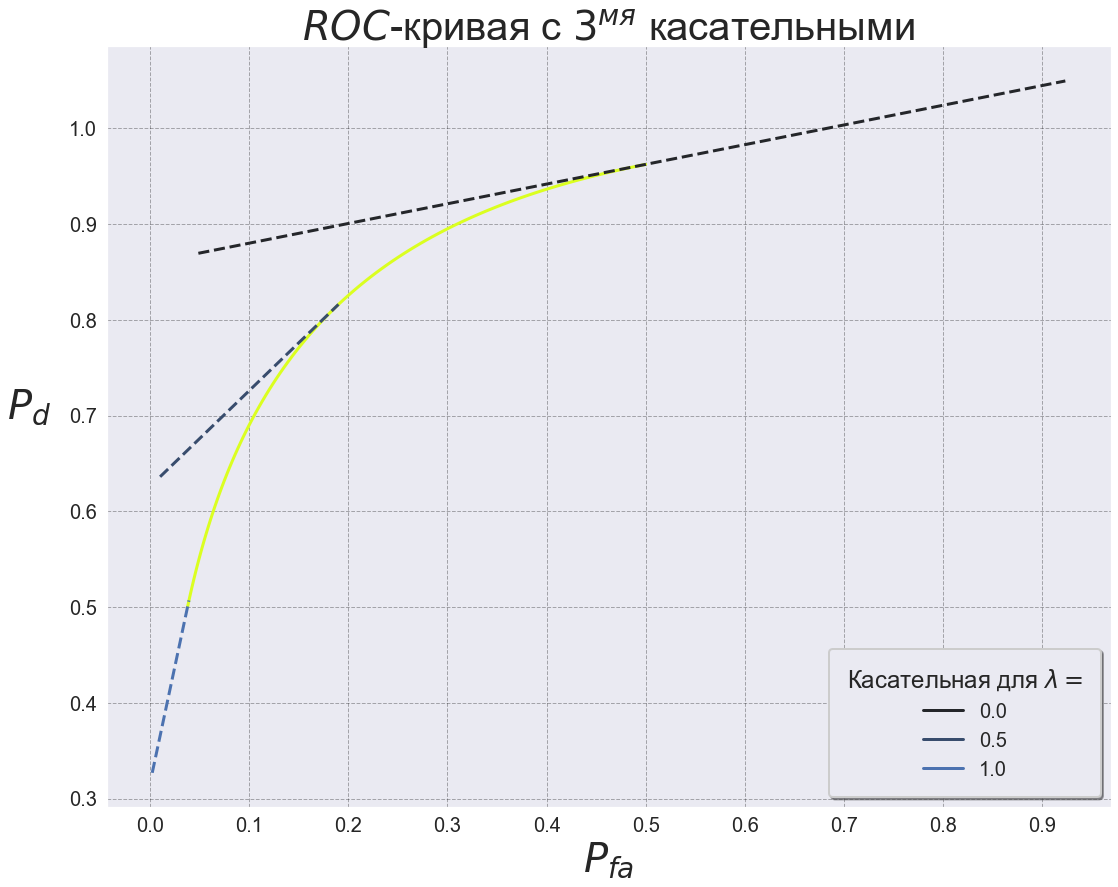
Рис. 10 ROC-кривая SNR=5 с тремя касательными в точках.
Рис. 10 ROC-кривая SNR=5 с тремя касательными в точках.

На рис. 10 рассматриваются точки \left(P_{f a}(0), P_{d}(0)\right),\left(P_{f a}(0.5), P_{d}(0.5)\right),\left(P_{f a}(1), P_{d}(1)\right).

Вывод

В ходе исследования были построены множество ROC-кривых на основе аналитического выражения (12). Были также получены свойства ROC-кривых на основе графиков и аналитических выражений. То, каким образом будет выглядеть характеристика рабочего приемника, зависит от значения SNR, из которого однозначно определяется значение σ. Также область, в которой определена ROC-кривая, зависит от диапазона λ.

Использованная литература

  • Ван-Трис Гарри Л. Теория обнаружения, оценок и модуляции. Том 1. Теория обнаружения, оценок и линейной модуляции -Нью-Йорк, 1968, Пер, с англ. , под ред. проф. В. И. Тихонова. М., «Советское радио», 1972, 744 с.

  • Тяпкин В.Н. Основы построения радиолокационных станций радиотехнических войск: учебник / В.Н. Тяпкин, А.Н. Фомин, Е.Н. Гарин [и др.]; под общ. ред. В.Н. Тяпкина. – Красноярск : Сиб. федер. ун-т. – 2011. – 536 с.

Дополнительно

Ссылка на github с исходным кодом.

ссылка на оригинал статьи https://habr.com/ru/post/549376/

Комментарии

Добавить комментарий

Ваш адрес email не будет опубликован. Обязательные поля помечены *