
Двойственная природа материи — широко известное понятие среди физиков. Вещество на атомном уровне в некоторых случаях ведёт себя как частицы, а в некоторых — как волны. Чтобы объяснить это, мы вводим волновую функцию частицы ψ(x, t), которая описывает не фактическое положение частицы, а вероятность нахождения частицы в данной точке. Волновая функция ψ(x, t), или поле вероятностей, которое удовлетворяет, возможно, самому важному уравнению в частных производных, по крайней мере для физиков, является уравнением Шрёдингера.
Одномерное уравнение Шрёдингера
Мы рассмотрим уравнение Шрёдингера в одном измерении. Метод решения волновой функции в двух или трёх измерениях в основном такой же, как и для одномерного. Но для визуализации и ради экономии времени мы будем придерживаться одного измерения. Выведем уравнение Шрёдингера для одномерного случая.
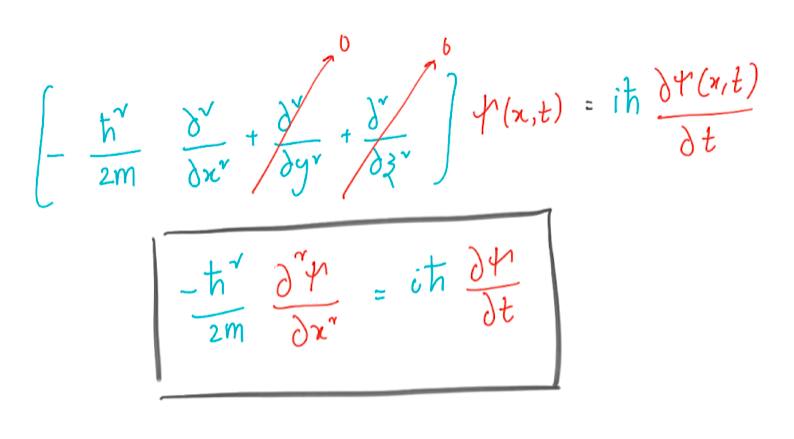
Решение частицы в ящике методом Кранка — Николсона
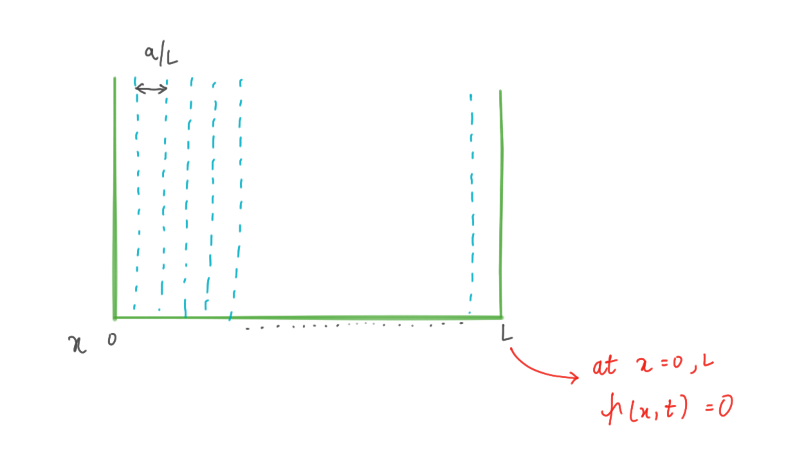
Решим волновое уравнение для нашей частицы, находящейся в ящике с непроницаемыми стенками. Идея состоит в том, чтобы решить уравнение в пространстве конечного размера. Но почему в непроницаемых стенах? Это условие заставляет волновую функцию равняться нулю на стенках, что мы положим при x=0 и x=L. Мы заменим вторую производную в уравнении Шрёдингера конечной разностью и применим метод Эйлера.
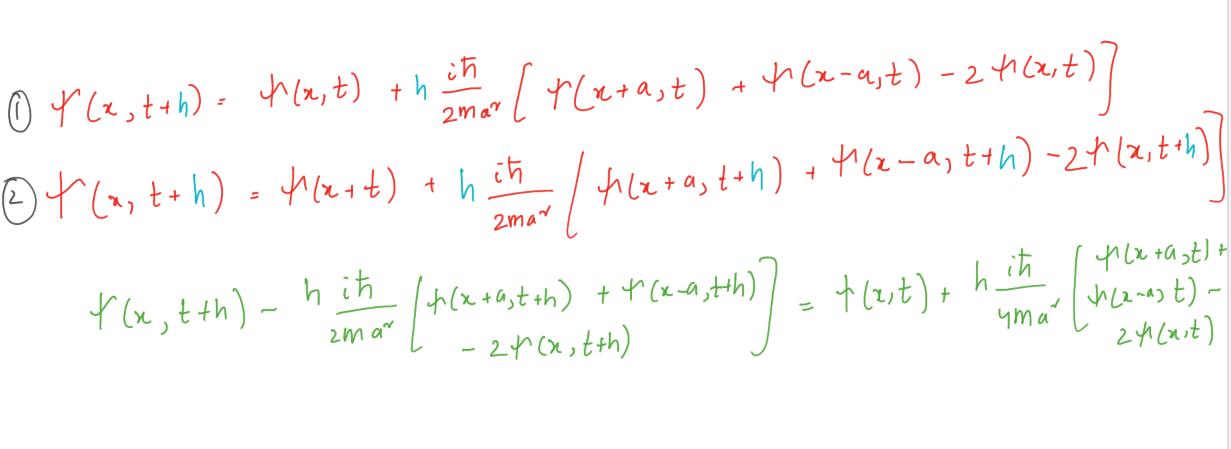
Приведённый выше вывод позволяет нам рекурсивно решить уравнение Шрёдингера. Граничные условия при x=0 и x=L для всех t волновая функция ψ(x, t)=0. Между этими точками у нас есть точки сетки в точках a, 2a, 3a и так далее. Сгруппируем значения ψ(x, t) в этих внутренних точках в вектор.
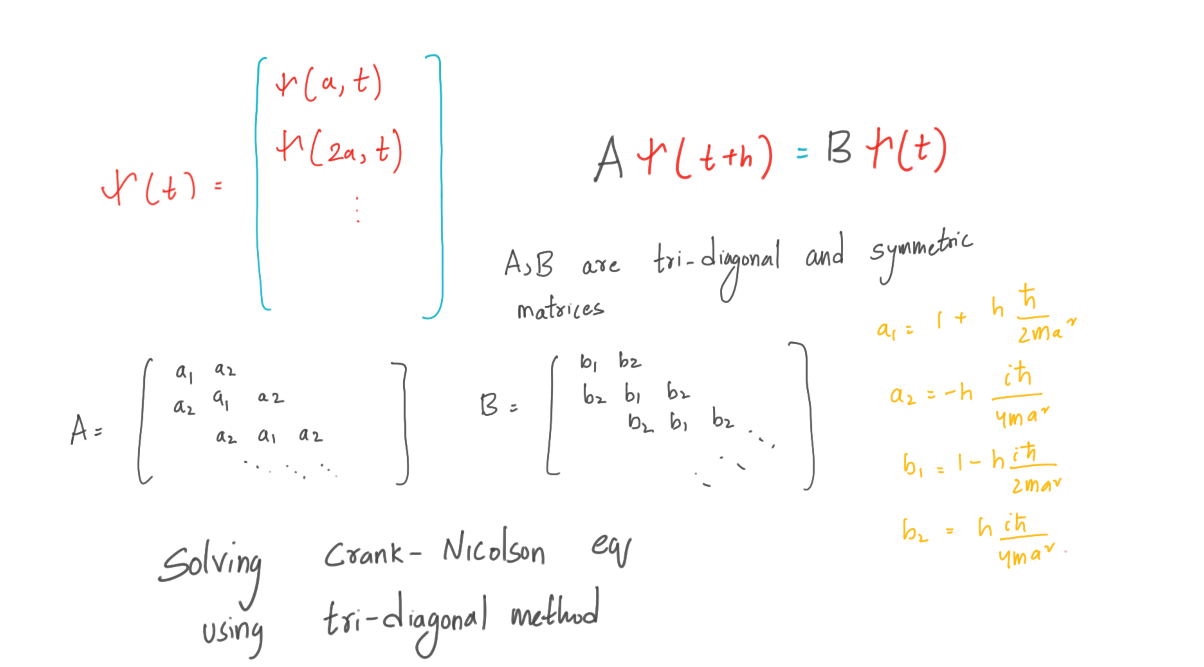
Теперь всё просто, у нас есть функция распространения: Aψ(t + h) = Bψ(t), где матрицы A и B являются симметричными и трёхдиагональными. Нам нужно будет инициализировать волновую функцию на временном шаге t = 0, ψ(0). Используя функцию распространения, мы можем аппроксимировать ψ(h), а затем, используя ψ(h), мы можем аппроксимировать ψ(2h) и так далее. В момент t = 0 волновая функция ψ(0) частицы имеет вид:
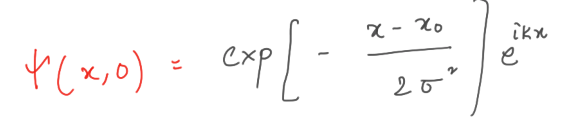
Это выражение для ψ(0) не нормализовано, и действительно должен быть общий коэффициент умножения, чтобы гарантировать, что плотность вероятности для частицы интегрируется в единицу.
Анимация волновой функции частицы в коробке
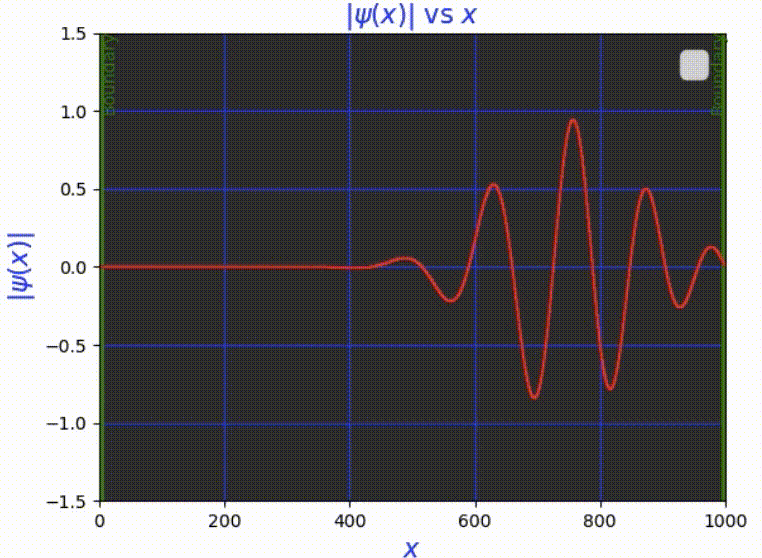
Мы попробуем оживить частицу в коробке с непроницаемыми стенками, используя метод Кранка — Николсона. Нам нужно будет вычислить вектор ψ(x, t) на всех временных шагах по сетке, учитывая начальную волновую функцию ψ(0) и используя пространственные срезы (N = 1000) с длиной среза = L/N.
Длинная простыня с кодом
import numpy as np from pylab import * from matplotlib import pyplot as plt from matplotlib import animation #matplotlib.use('GTK3Agg') # from matplotlib import interactive # interactive(True) ########################################Variables###################################################################################################### N_Slices = 1000 #Number of slices in the box Time_step = 1e-18 #Time step for each iteration Mass = 9.109e-31 #mass of electron plank = 1.0546e-36 #Planks constant L_Box = 1e-9 #Length of the box Grid = L_Box/N_Slices #Lenght of each slice #####################################Si(0) using the given equation ############################################################################### Si_0 = np.zeros(N_Slices+1,complex) #Initiating Si funtion at time step = 0 x = np.linspace(0,L_Box,N_Slices+1) def G_Equation(x): x_0 = L_Box/2 Sig = 1e-10 k = 5e10 result = exp(-(x-x_0)**2/2/Sig**2)*exp(1j*k*x) #Given Equation at t = 0 return result Si_0[:] = G_Equation(x) #Si funtion at time step = 0 #######################################V = Bxsi(0)################################################################################ a_1 = 1 + Time_step*plank*1j/(2*Mass*(Grid**2)) #Diagonal of A Tridiagonal matrix a_2 = -Time_step*plank*1j/(4*Mass*Grid**2) #Up and Down to A Tridiagonal matrix b_1 = 1 - Time_step*plank*1j/(2*Mass*(Grid**2)) #Diagonal of B Tridiagonal matrix b_2 = Time_step*plank*1j/(4*Mass*Grid**2) #Up and Down to B Tridiagonal matrix BxSi_0 = [] #V = BxSi and si funtion at x = 0 for i in range(1000): if i == 0: BxSi_0.append(b_1*Si_0[0] + b_2*(Si_0[1])) #V can be maipulated by the equation in Text book else: BxSi_0.append(b_1*Si_0[i] + b_2*(Si_0[i+1] + Si_0[i-1])) BxSi_0 = np.array(BxSi_0) #####################################Tri Diagonal matrix algorithm##################################################################################### def TDMAsolver(a, b, c, d): #Instead of solving using Numpy.linalg, it is prefered to Use nf = len(d) #Tri Diagonal Matrix algorithm ac, bc, cc, dc = map(np.array, (a, b, c, d)) # a,b,c's are up,dia,down element in tridiagonl matrix A for it in range(1, nf): #AX = d mc = ac[it-1]/bc[it-1] bc[it] = bc[it] - mc*cc[it-1] dc[it] = dc[it] - mc*dc[it-1] xc = bc xc[-1] = dc[-1]/bc[-1] for il in range(nf-2, -1, -1): xc[il] = (dc[il]-cc[il]*xc[il+1])/bc[il] return xc global a #A matrix is fixed through out the problem, so it is good to globalize the variables global b global c b = N_Slices*[a_1] #In A matrix, Both Up,Down elements are a_2 and diag matrix is a_1 a = (N_Slices-1)*[a_2] c = (N_Slices-1)*[a_2] ####################################Si 1st funtion solver#################################################################################### global Si_1 #First si_funtion usinf Axsi(0+h) = BxSi(0) Si_1 = TDMAsolver(a, b, c, BxSi_0) #This can be solved by TDM(A,BxSi(0)) ###################################A funtion which caliculates si at each step##################################################################################### global Si_sd #AxSi_stepup = BxSi_stepdown Si_sd = {} #At first Buckting Si_stepdown in to directry which we can using for finding Si_stepup def sifuntion(i): #In next iteration, Last iteration Si_stepup will be this iteration's Si_stepdown if i == 0: Si_sd[0] = Si_1 return Si_1 else: Si_stepdown = Si_sd[i-1] V = np.zeros(N_Slices,complex) V[0] = b_1*Si_stepdown[0] + b_2*(Si_stepdown[1]) V[1:N_Slices-1] = b_1*Si_stepdown[1:N_Slices-1] + b_2*(Si_stepdown[2:N_Slices] + Si_stepdown[0:N_Slices-2]) V[N_Slices-1] = b_1*Si_stepdown[N_Slices-1]+ b_2*(Si_stepdown[N_Slices-2]) Si_stepup = TDMAsolver(a, b, c, V) Si_sd[i] = Si_stepup x = Si_stepup.real return x ####################################Animating####################################################################################### fig = plt.figure() ax = plt.axes(xlim=(0, 1000), ylim=(-1.5, 1.5)) line, = ax.plot([], [], lw=5) ax.legend(prop=dict(size=20)) ax.set_facecolor('black') ax.patch.set_alpha(0.8) ax.set_xlabel('$x$',fontsize = 15,color = 'blue') ax.set_ylabel(r'$|\psi(x)|$',fontsize = 15,color = 'blue') ax.grid(color = 'blue') ax.set_title(r'$|\psi(x)|$ vs $x$', color='blue',fontsize = 15 ) line, = ax.step([], []) def init(): line.set_data([], []) return line, def animate(i): x = np.linspace(0, 1000, num=1000) y = sifuntion(i) line.set_data(x, y) line.set_color('red') return line, anim = animation.FuncAnimation(fig, animate, init_func=init, frames=10**5, interval=1, blit=True)#5*10**5 plt.vlines(1, -5, 5, linestyles = 'solid', color= 'green',lw=5) plt.vlines(999, -5, 5, linestyles = 'solid', color= 'green',lw=5) plt.text(1,1,'Boundary',rotation=90,color= 'green' ) plt.text(975,1,'Boundary',rotation=90,color= 'green' ) plt.figure(figsize=(10,10)) plt.show() # Writer = animation.writers['ffmpeg'] # writer = Writer() # anim.save('im.mp4', writer=writer) 
Узнайте, как прокачаться в других специальностях или освоить их с нуля:
Другие профессии и курсы
ПРОФЕССИИ
КУРСЫ
ссылка на оригинал статьи https://habr.com/ru/company/skillfactory/blog/549470/
Добавить комментарий