Как регулировать мощность переменного тока

Решил как-то отец собрать для дачи некое устройство, в котором, по его заверению, можно будет варить сыр. Устройство сие вид имело могучий и представляло из себя железный короб, подозрительно напоминающий старую стиральную машинку. Внутрь короба (все также добротно!) были вмонтированы три тэна по 1700 Ватт каждый. В общем сыра должно было хватить на небольшой посёлок.

Изделие (внешне выглядящее как что-то из безумного макса), должно быть весьма технологичным и поддерживать заданную температуру в максимально узких пределах. Для этого рядом появилась ещё одна коробка с симисторами, к которым подключались ТЭНы и схема, выдающая высокий уровень при переходе синусоиды через ноль. А у меня появился интересный проект.

Итак нам нужно выходить на заданную температуру и поддерживать её, с этим должен справляться алгоритм ПИД регулятора. Глубоко вдаваться в его работу не буду, скажу лишь что он получает на вход текущую ошибку, а на выходе выдает какое-то число в заданных пределах. У меня таким числом будет мощность выдаваемая на ТЭН, хотя в принципе, это может быть любой инерционный процесс, например обороты двигателя. Что важно для ПИД регулятора, это чтобы выходная величина производила воздействие линейно. Поэтому попробуем разобраться в способах регулировки мощности и их линейности.

Как вообще регулируется мощность?

Мощность — это произведение силы тока на напряжение. Если представить это произведение графически, то для постоянного тока, это будет площадь прямоугольника со сторонами равными напряжению и току

Так как при постоянном сопротивлении и напряжении ток тоже будет постоянным, то заменим ось тока на ось времени. Сопротивление я беру постоянным для объяснения принципа регулирования.

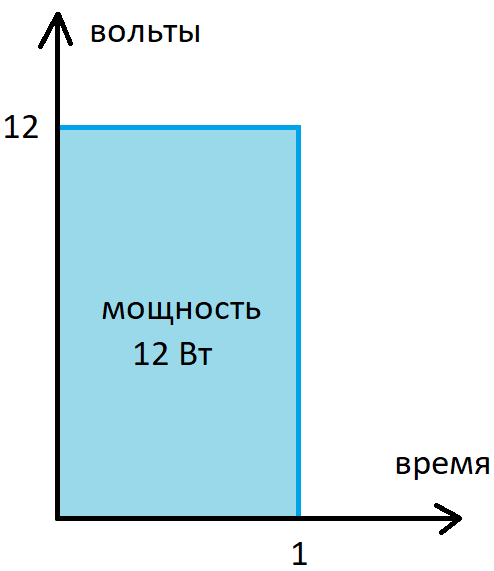
Тогда при заданном напряжении (12 В) и сопротивлении в 1 Ом, по закону Ома: I=U/R, получаем ток равный 1 А, и соответственно мощность за единицу времени будет равна 12 Вт. При другом сопротивлении мощность, естественно тоже изменится.

Теперь, если мы хотим регулировать мощность за единицу времени, нам нужно как-то изменять площадь фигуры за единицу времени. Самым чистым способом будет просто изменять напряжение, тогда и мощность будет пропорционально изменяться. Но контроллер, как и любые цифровые устройства, не умеет плавно изменять напряжение на ножках, он может либо «поднимать» их до высокого уровня, либо «опускать» до низкого уровня. Этот недостаток он компенсирует скоростью, даже самый дохленький современный МК может работать на частотах в миллионы тактов в секунду. Чтобы регулировать мощность, контроллер будет очень быстро «дрыгать» ножкой, тем самым изменяя результирующая площадь импульса за единицу времени.

На этом принципе устроена широтно-импульсная модуляция, она же ШИМ. Изменяя время (ширину) импульса за период мы изменяем выдаваемую мощность. На рисунке выше, показано два периода ШИМа. Каждый период имеет отношение площади импульса к площади всего периода 0.5, те половину времени периода контроллер выдает высокий уровень сигнала, другую половину низкий. Отношение времени высокого уровня сигнала к времени низкого называется скважностью. Красная линия на графике отражает результирующую мощность за единицу времени, по ней видно что при скважности 0.5 мощность также упала на половину (с 12 до 6 Вт). Хорошая новость состоит в том, что, ШИМ в контроллерах реализован аппаратно. Так что для регулирования чего-то достаточно его запустить и, по необходимости, изменять скважность.

Для постоянного тока, режим ШИМа оптимален, причем чем более инерционный прибор мы к нему подключаем, тем меньшую частоту ШИМа можно использовать. Для большого ТЭНа достаточно чуть ли не одного герца, а вот для светодиодов лучше использовать частоту побольше. Кстати частота ШИМа в подсветке экрана ноутбука, зачастую оказывается чуть ли не решающим фактором при покупке, так как, при слишком низкой частоте, глаза будут быстро уставать.

Если попробовать провернуть трюк с ШИМом для переменного напряжения, мы увидим что все сломалось и мощность перестала регулироваться линейно

одинаковые промежутки времени стали давать нам разную площадь, а значит разную мощность. Однако, если разбить полученные отрезки на на ещё более мелкие, то процентное соотношение ширины импульса к ширине кусочка будет выравниваться.

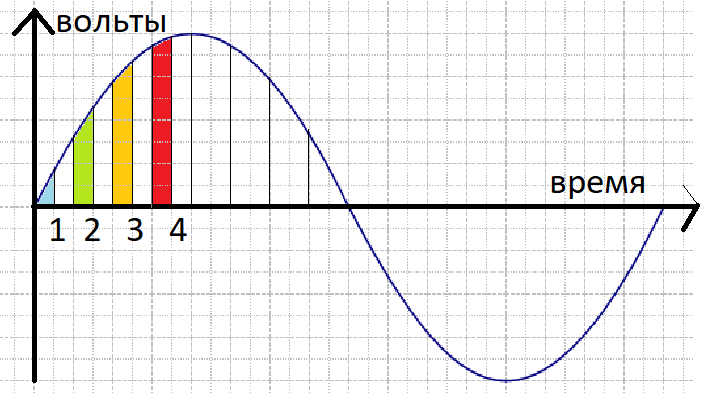
Если мы возьмем равный процент выдаваемой мощности от каждого кусочка, в результате мы получим такой же процент, от мощности всей волны, а на выходе мы получим линейный регулятор мощности для переменного тока. Причем чем большую частоту будет иметь ШИМа, тем на большее количество кусочков он разобьет синусоиду, а значит мы получим большую линейность.

Это было бы решением всех проблем, но в моем случае устройством коммутировавшим нагрузку был не быстрый транзистор, а симистор — медленный прибор, с максимальными рабочими частотами в пределах нескольких сотен герц, к тому же симистор можно только открыть, закроется он сам при переходе через ноль. На таких частотах управлять переменным напряжением которое имеет частоту 50 Гц, линейно не получится. Поэтому здесь нужно использовать какой-то другой подход и как раз для него, помимо симисторов, была установлена схема перехода через ноль.

В случае с симисторами лучше разбить синусоиду на куски с одинаковыми площадями и записать время каждого такого кусочка в таблицу. Тогда каждое последующее значение из таблицы будет линейно увеличивать мощность.

На графике выше полуволна синусоиды разбита на части разные по времени, но имеющие одинаковую площадь, а значит несущие в себе одинаковую мощность. Все что нам останется сделать это загрузить таблицу с временными интервалам в наш котроллер, синхронизировать какой-то из его таймеров с частотой синусоиды, для этого используется схема перехода через ноль, и просто брать из таблички нужное значение, в течении которого будет высокий уровень. Суть метода похожа на ШИМ, но немного доработанный и синхронизированный с источником переменного напряжения.

Расчёт таблицы мощности

Теперь можно перейти непосредственно к расчёту)

Изначально задача заключается в том чтобы разбить синусоиду на нужное нам количество кусочков, каждый из которых будет иметь одинаковую площадь. На этом моменте, обычно проступает холодный пот, так-как площадь под графиком это и есть геометрическое определение интеграла. Соответственно нам нужно будет взять интеграл от синуса и при этом определить такие пределы интегрирования, которые будут давать одинаковый результат. Затем (как будто расчёта интегралов мало!) полученные пределы нужно будет перевести во время задержки (время в течении которого будет сохранятся высокий уровень). После чего полученное время перевести в понятное для контроллера число — количество тиков таймера. Звучит страшно, а по факту сейчас разберёмся:

Интеграл от синуса является простейшим табличным интегралом и равен -cos(x)+C Вот и всё) неопределенный интеграл найден.

Теперь нужно подобрать пределы для определенных интегралов. Выберем, насколько частей мы хотим разбить нашу синусоиду: я выбрал сто, чтобы можно было регулировать мощность с шагом в 1%.

Итак мы нашли чему будет равен неопределённый интеграл и даже выбрали шаг. Теперь нужно подобрать пределы интегрирования. Смысл их подбора заключается в том, чтобы значение определенного интеграла было постоянным при их смене. Напомню, что неопределенный интеграл это формула, а определённый вполне конкретное число. Определённый интеграл считается по формуле:

То есть мы берем неопределённый интеграл (в нашем случае это -cos(x) ), подставляем в него верхнее число, затем нижнее, и вычитаем второе из первого.

Подбирать пределы в лоб будет сложно и долго, поэтому вспомним тригонометрию, а конкретно арк функции.

Арк функции — суть обратные тригонометрические функции, которые позволяют определить от какого ‘x’ получен результат. То есть, если (-cos(b))-(-cos(a)) даст нам значение площади между a и b, то arccos от нужного кусочка площади даст нам значение пределов такого кусочка. Если быть точным то так мы найдем только верхний предел, первого кусочка, все остальные мы получим добавляя к площади размер шага, то есть сначала найдем arccos(ед. площади), потом arccos(ед. площади *2) и так далее. При этом каждый ответ будет являться нижним пределом для следующего кусочка.

Теперь взглянем на график косинуса:

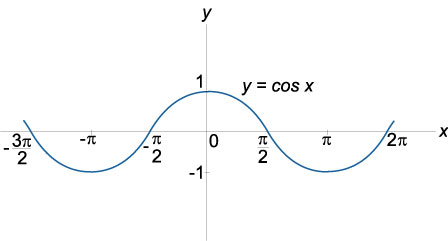
Для того чтобы найти все необходимые задержки, нам нужно найти значения всего одной четверти. Всё остальное это её зеркальное отражение либо относительно оси x, либо относительно оси y. Тогда если мы хотим получить 100 значений, нам нужно найти всего 50 первых. Будем искать значения арккосинуса от 1 до 0 с шагом 50. Можно использовать лист и бумажку чтобы попрактиковаться в математике, можно онлайн калькулятор, я же буду использовать Python и функцию arccos, библиотеки numpy:

import numpy as np # с помощью генератора списка находим все арккосинусы от 0 до 1 с шагом две сотых rad_arr=[np.arccos(x) for x in np.arange(0,1,0.02)]

Отлично мы получили массив чисел (пределов интегрирования!), валидность этих чисел можно проверить подставив их в интеграл. В результате должна получится площадь равная выбранному шагу! Если все сошлось, то можно двигаться дальше и задать получившимся числам размерность времени, потому что сейчас они в радианах. Чтобы это сделать нужно выяснить угловую скорость, для частоты сети, то есть количество радиан в секунду.

Тогда узнаем сколько сколько длится одна радиана

Теперь, значения задержек в радианах, превратим во время, умножив каждое значение на период радианы (T). Проверим ход своей мысли: действительно-ли получится время задержки, если умножить задержку, на период? Задержка имеет размерность радиан, период — секунд за радиану, мы хотим их перемножить. Тогда рад * ( сек / рад ) = сек. Мы получили время, а значит ход мыслей должен быть верным.

Для расчётов я опять предпочту python:

#стандартная частота сети frequency = 50 #находим частоту в радианах rad_per_s=frequency*(2*math.pi) #находим период радианы s_per_rad=1/rad_per_s #находим задержки используя полученный ранее массив delay_arr=[x*s_per_rad for x in rad_arr]

На этом моменте мы получили универсальную таблицу задержек, теперь необходимо конвертировать её специально под микроконтроллер.

Расчёт таймера МК и перевод таблицы

Время необходимо перевести в понятную для МК величину — количество переполнений таймера. Но сначала необходимо определится с частотой таймера: чем выше частота, тем точнее он будет отмерять время, но с другой стороны, тем меньше времени будет оставаться на выполнение остальной программы. Здесь необходимо найти золотую середину.

Для определения минимально допустимой частоты таймера, надо найти числа в массиве с минимальной разностью между ними. Разность тем меньше, чем ближе в максимуму синусоиды мы двигаемся. Тогда возьмем задержку при которой синусоида достигает единицы и число перед ним, после чего найдем их разность:

5 мс — 4.9363 мс = 0.0636 мс

Получившееся число является максимально допустимым периодом между прерываниями таймера, тогда через него найдём минимально допустимую частоту

1 / 0.0636 = 15 КГц

Значит для заданной точности в 1% будет достаточно таймера с частотой 15КГц. Частота МК составляет 16 МГц, значит между прерываниями будет 1000 тактов процессора, этого достаточно для выполнения остальной части программы, так что можно смело настраивать таймер на заданную частоту.

Для настройки таймера на определенную частоту, не кратную тактирующей используется режим таймера CTC — Clear Timer on Compare. В этом режиме таймер досчитывает до заданного числа и сбрасывается, после чего операция повторяется. Число при котором будет происходить совпадение считается по формуле

Число = Тактовая частота МК / предделитель таймера / выбранная частота

Частота выбрана, теперь нужно перевести таблицу в тики таймера. Делать я это буду опять на Python

#задаем частоту таймера generator_freg=15000 #получаем время одного периода таймера one_tick=1/generator_freq #получаем массив с тиками таймера tick_arr=[x/one_tick for x in delay_arr]

В общем-то на этом весь расчёт окончен, остается только отзеркалить получившийся массив для второй половины полуволны и загрузить в МК. Далее по прерыванию от синхроимпульса, нужно подать низкий уровень, на ножку управления симистором, запустить таймер и считать его переполнения (совпадения, тк у нас режим CTC). Как только количество переполнений достигнет нужного числа из таблички, подаем высокий уровень на управляющую ножку. На этом линейный регулятор мощности переменного напряжения готов!

Заключение

Надеюсь статья была понятна и её было интересно читать. В дополнение хотелось бы сказать, сигнал перехода через ноль не приходит идеально вовремя, поэтому может потребоваться дополнительная коррекция, чтобы это исправить.

Код расчетов на python

import math import numpy as np  rad_arr = [np.arccos(x) for x in np.arange(1, 0, 0.02)]  frequency = 50 rad_per_s = frequency * (2 * math.pi) s_per_rad = 1 / rad_per_s  delay_arr = [x * s_per_rad for x in rad_arr]  generator_freg = 15000 one_tick = 1 / generator_freg  tick_arr = [x / one_tick for x in rad_arr]  print(tick_arr) 

Также, если кому-то будет интересно, могу поделится исходником готового регулятора для ардуино.