
Оптимизация функций — это область исследований, где поставлена задача найти некое входное значение [аргумент функции], результат которого — максимум или минимум данной функции. Алгоритмов оптимизации много, поэтому важно развивать алгоритмическое чутьё и исследовать алгоритмы на простых и легко визуализируемых тестовых функциях.
Двумерные функции принимают два входных значения (x и y) и выводят единожды вычисленное на основе входа значение. Эти функции — одни из самых простых для изучения оптимизации. Их преимущество в том, что они могут визуализироваться в виде контурного графика или графика поверхности, показывающего топографию проблемной области с оптимумом и уникальными элементами, которые отмечены точками. В этом туториале вы ознакомитесь со стандартными двумерными тестовыми функциями, которые можно использовать при изучении оптимизации функций. Давайте начнём.
Обзор туториала
Двумерная функция — это функция, которая принимает две входные переменные и вычисляет целевое значение. Можно представить две входные переменные как две оси на графике, x и y. Каждый вход в функцию является единственной точкой на графике, а результат вычисления функции — некоторая высота на графике.
Такая визуализация позволяет концептуализировать функцию в виде поверхности, так мы сможем охарактеризовать функцию по структуре поверхности. Например, возвышенности указывают на большие значения целевой функции, а провалы — на небольшие.
Поверхность может иметь один основной оптимум или же много точек для оптимизации, в которых можно, говоря образно, застрять. Также она может быть гладкой, шумной, выпуклой, может иметь иные всевозможные свойства, которые важны в смысле алгоритмов оптимизации. Мы могли бы использовать множество других типов двумерных функций.
Вместе с тем, есть много стандартных тестовых функций, применяемых в области оптимизации, а также тестовые функции со специфическими свойствами, которые мы можем применять, когда тестируем различные алгоритмы. Рассмотрим несколько простых двумерных тестовых функций, разделив их на две группы согласно свойствам:
-
Унимодальные функции.
-
Унимодальная функция 1.
-
Унимодальная функция 2.
-
Унимодальная функция 3.
-
Мультимодальные функции.
-
Мультимодальная функция 1.
-
Мультимодальная функция 2.
-
Мультимодальная функция 3.
Реализация каждой целевой функции будет представлена на Python в выведена в виде поверхности.
Все целевые функции являются функциями минимизации, то есть задача — найти аргументы, при которых значение функции минимально. Любая максимизирующая функция может быть заменена функцией минимизации путем добавления минуса ко всем её значениям. Аналогичным образом минимизирующая функция заменяется максимизирующей. Кроме того, все функции взяты из литературы, их придумал не я. Ссылки смотрите в разделе «Дальнейшее чтение».
Вы можете выбрать, скопировать и вставить в код одну или несколько функций, чтобы использовать их в вашем собственном проекте, посвящённом изучению или сравнению поведения алгоритмов оптимизации.
Унимодальные функции
Унимодальность означает, что функция имеет единственный глобальный оптимум.
Унимодальная функция может быть выпуклой и невыпуклой. Выпуклая функция — это функция, на агрфике которой между двумя любыми точками можно провести линию и эта линия останется в домене. В случае двумерной функции это означает, что поверхность имеет форму чаши, а линии между двумя точками проходят по чаше или внутри неё. Давайте рассмотрим несколько примеров унимодальных функций.
Унимодальная функция 1
Диапазон ограничен промежутком -5,0 и 5,0 и одним глобальным оптимумом в точке [0,0, 0,0].
# unimodal test function from numpy import arange from numpy import meshgrid from matplotlib import pyplot from mpl_toolkits.mplot3d import Axes3D # objective function def objective(x, y): return x**2.0 + y**2.0 # define range for input r_min, r_max = -5.0, 5.0 # sample input range uniformly at 0.1 increments xaxis = arange(r_min, r_max, 0.1) yaxis = arange(r_min, r_max, 0.1) # create a mesh from the axis x, y = meshgrid(xaxis, yaxis) # compute targets results = objective(x, y) # create a surface plot with the jet color scheme figure = pyplot.figure() axis = figure.gca(projection='3d') axis.plot_surface(x, y, results, cmap='jet') # show the plot pyplot.show()Код создаёт поверхность согласно графику функции.
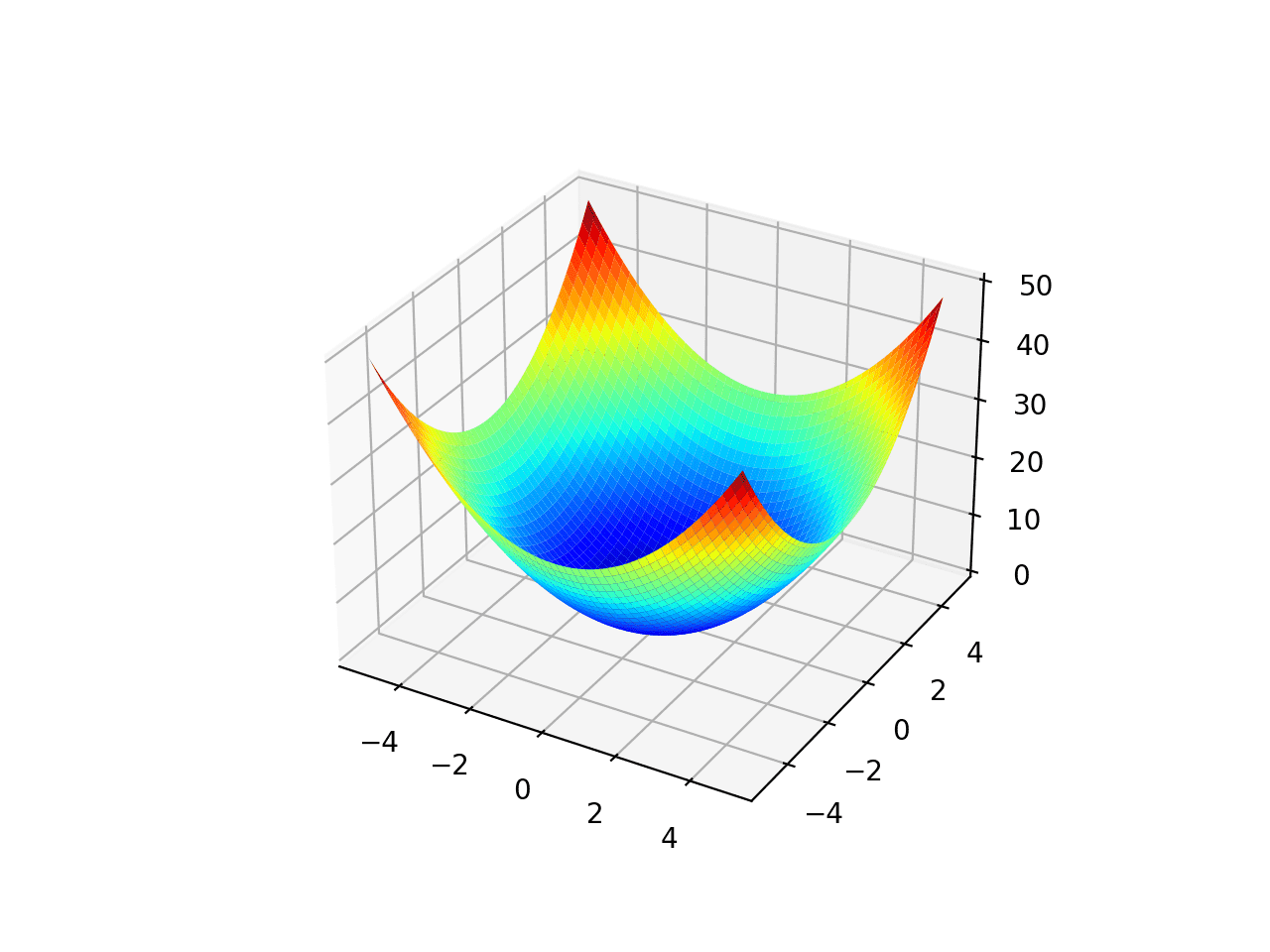
Унимодальная функция 2
Диапазон ограничен значениями -10,0 и 10,0 и одним глобальным оптимумом в точке [0,0, 0,0].
# unimodal test function from numpy import arange from numpy import meshgrid from matplotlib import pyplot from mpl_toolkits.mplot3d import Axes3D # objective function def objective(x, y): return 0.26 * (x**2 + y**2) - 0.48 * x * y # define range for input r_min, r_max = -10.0, 10.0 # sample input range uniformly at 0.1 increments xaxis = arange(r_min, r_max, 0.1) yaxis = arange(r_min, r_max, 0.1) # create a mesh from the axis x, y = meshgrid(xaxis, yaxis) # compute targets results = objective(x, y) # create a surface plot with the jet color scheme figure = pyplot.figure() axis = figure.gca(projection='3d') axis.plot_surface(x, y, results, cmap='jet') # show the plot pyplot.show()Код создаёт поверхность согласно графику функции.
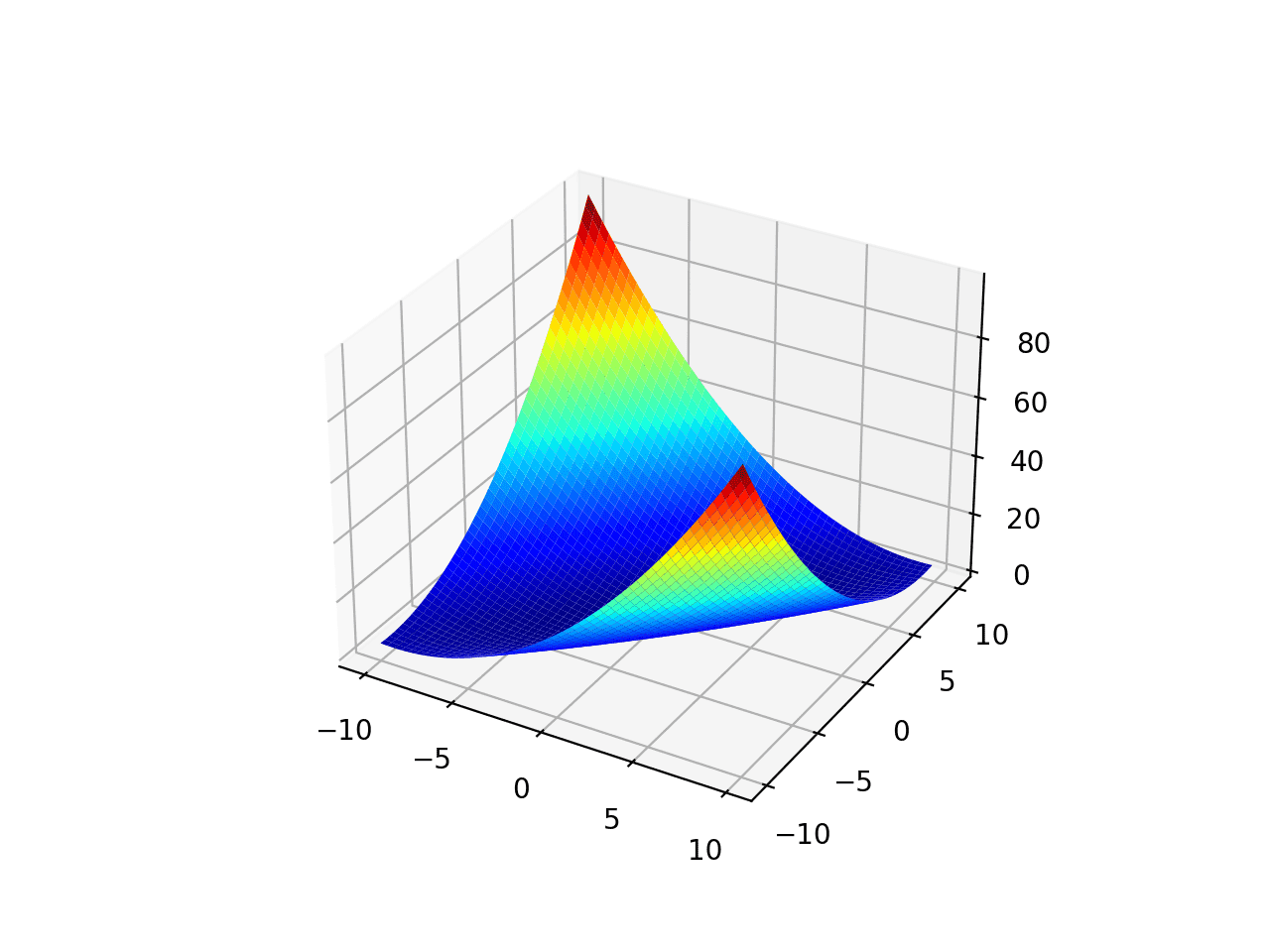
Унимодальная функция 3
Диапазон ограничен -10,0 и 10,0 и одним глобальным оптимумом при [0,0, 0,0], функция известна как функция Изома.
# unimodal test function from numpy import cos from numpy import exp from numpy import pi from numpy import arange from numpy import meshgrid from matplotlib import pyplot from mpl_toolkits.mplot3d import Axes3D # objective function def objective(x, y): return -cos(x) * cos(y) * exp(-((x - pi)**2 + (y - pi)**2)) # define range for input r_min, r_max = -10, 10 # sample input range uniformly at 0.01 increments xaxis = arange(r_min, r_max, 0.01) yaxis = arange(r_min, r_max, 0.01) # create a mesh from the axis x, y = meshgrid(xaxis, yaxis) # compute targets results = objective(x, y) # create a surface plot with the jet color scheme figure = pyplot.figure() axis = figure.gca(projection='3d') axis.plot_surface(x, y, results, cmap='jet') # show the plot pyplot.show()Код создаёт поверхность согласно графику функции.
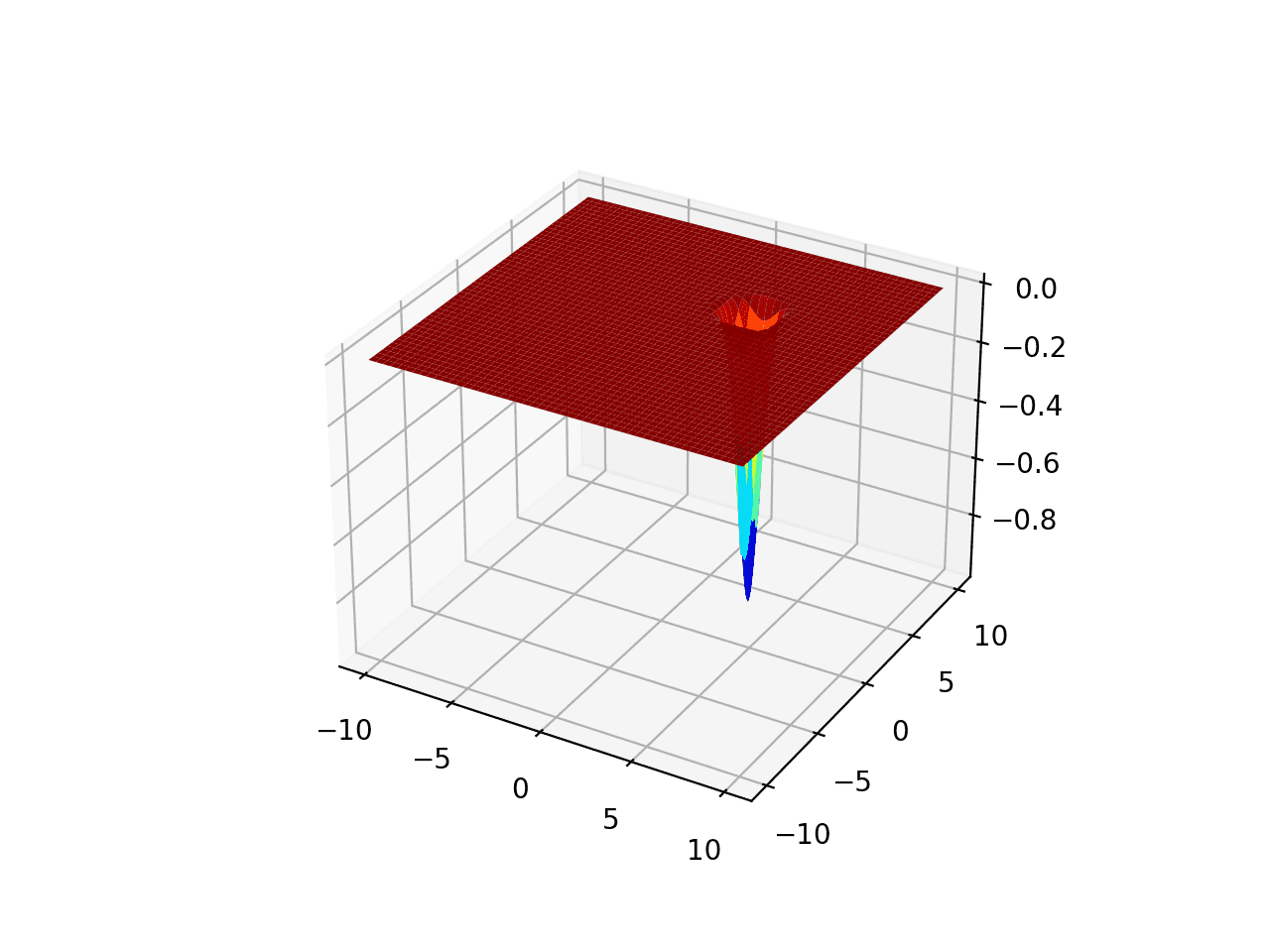
Мультимодальные функции
Мультимодальная функция — это функция с более чем одной “модой” или оптимумом (например долиной на графике).
Мультимодальные функции являются невыпуклыми. Могут иметь место один или несколько ложных оптимумов. С другой стороны, может существовать и несколько глобальных оптимумов, например несколько различных значений аргументов функции, при которых она достигает минимума.
Вот несколько примеров мультимодальных функций.
Мультимодальная функция 1
Диапазон ограничен -5,0 и 5,0 и одним глобальным оптимумом при [0,0, 0,0]. Эта функция известна как функция Экли.
# multimodal test function from numpy import arange from numpy import exp from numpy import sqrt from numpy import cos from numpy import e from numpy import pi from numpy import meshgrid from matplotlib import pyplot from mpl_toolkits.mplot3d import Axes3D # objective function def objective(x, y): return -20.0 * exp(-0.2 * sqrt(0.5 * (x**2 + y**2))) - exp(0.5 * (cos(2 * pi * x) + cos(2 * pi * y))) + e + 20 # define range for input r_min, r_max = -5.0, 5.0 # sample input range uniformly at 0.1 increments xaxis = arange(r_min, r_max, 0.1) yaxis = arange(r_min, r_max, 0.1) # create a mesh from the axis x, y = meshgrid(xaxis, yaxis) # compute targets results = objective(x, y) # create a surface plot with the jet color scheme figure = pyplot.figure() axis = figure.gca(projection='3d') axis.plot_surface(x, y, results, cmap='jet') # show the plot pyplot.show()Код создаёт поверхность согласно графику функции.

Мультимодальная функция 2
Диапазон ограничен [-5,0 и 5,0], а функция имеет четыре глобальных оптимума при [3,0, 2,0], [-2,805118, 3,131312], [-3,779310, -3,283186], [3,584428, -1,848126]. Эта функция известна как функция Химмельблау.
# multimodal test function from numpy import arange from numpy import meshgrid from matplotlib import pyplot from mpl_toolkits.mplot3d import Axes3D # objective function def objective(x, y): return (x**2 + y - 11)**2 + (x + y**2 -7)**2 # define range for input r_min, r_max = -5.0, 5.0 # sample input range uniformly at 0.1 increments xaxis = arange(r_min, r_max, 0.1) yaxis = arange(r_min, r_max, 0.1) # create a mesh from the axis x, y = meshgrid(xaxis, yaxis) # compute targets results = objective(x, y) # create a surface plot with the jet color scheme figure = pyplot.figure() axis = figure.gca(projection='3d') axis.plot_surface(x, y, results, cmap='jet') # show the plot pyplot.show()Код создаёт поверхность согласно графику функции.
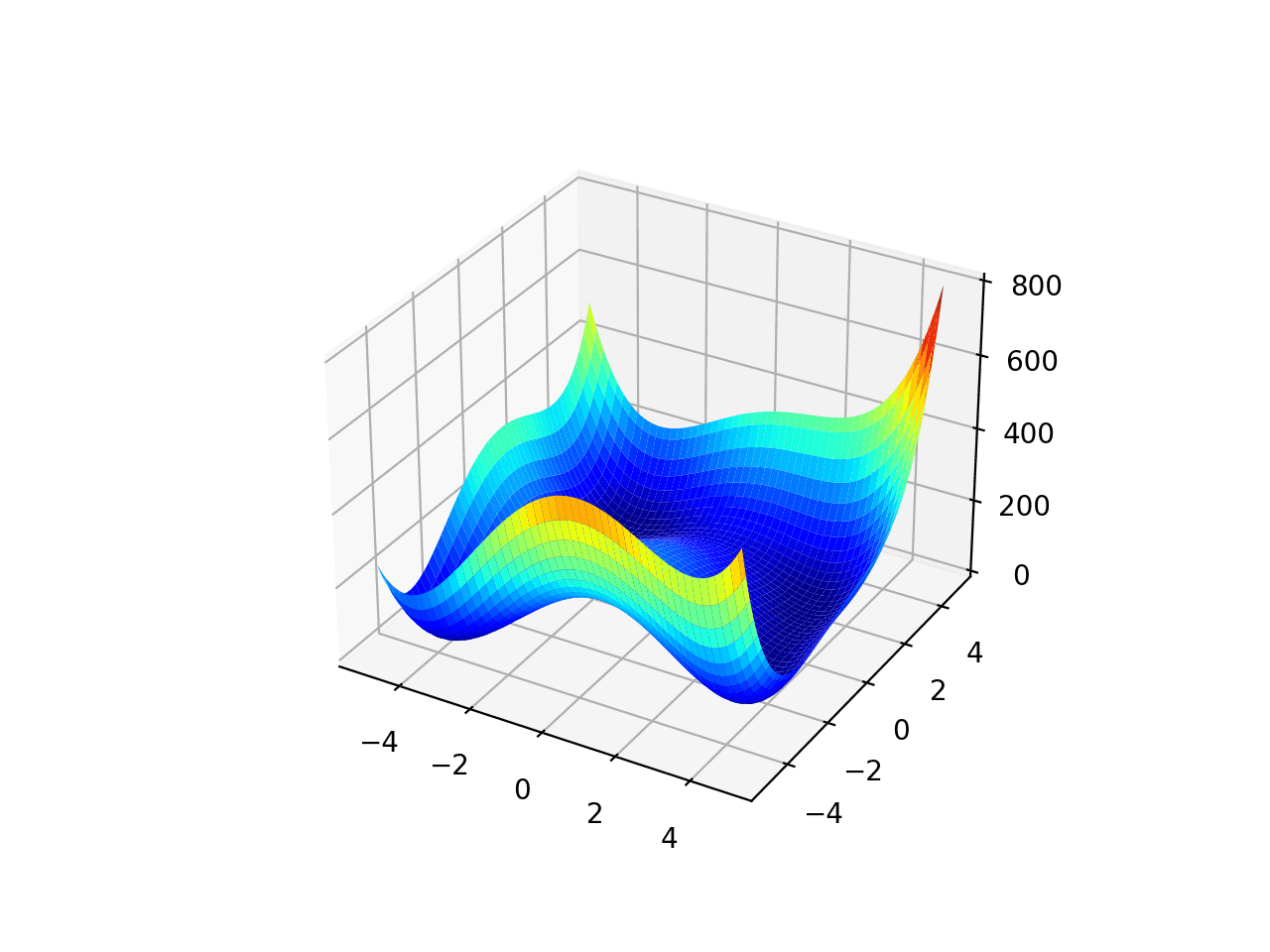
Мультимодальная функция 3
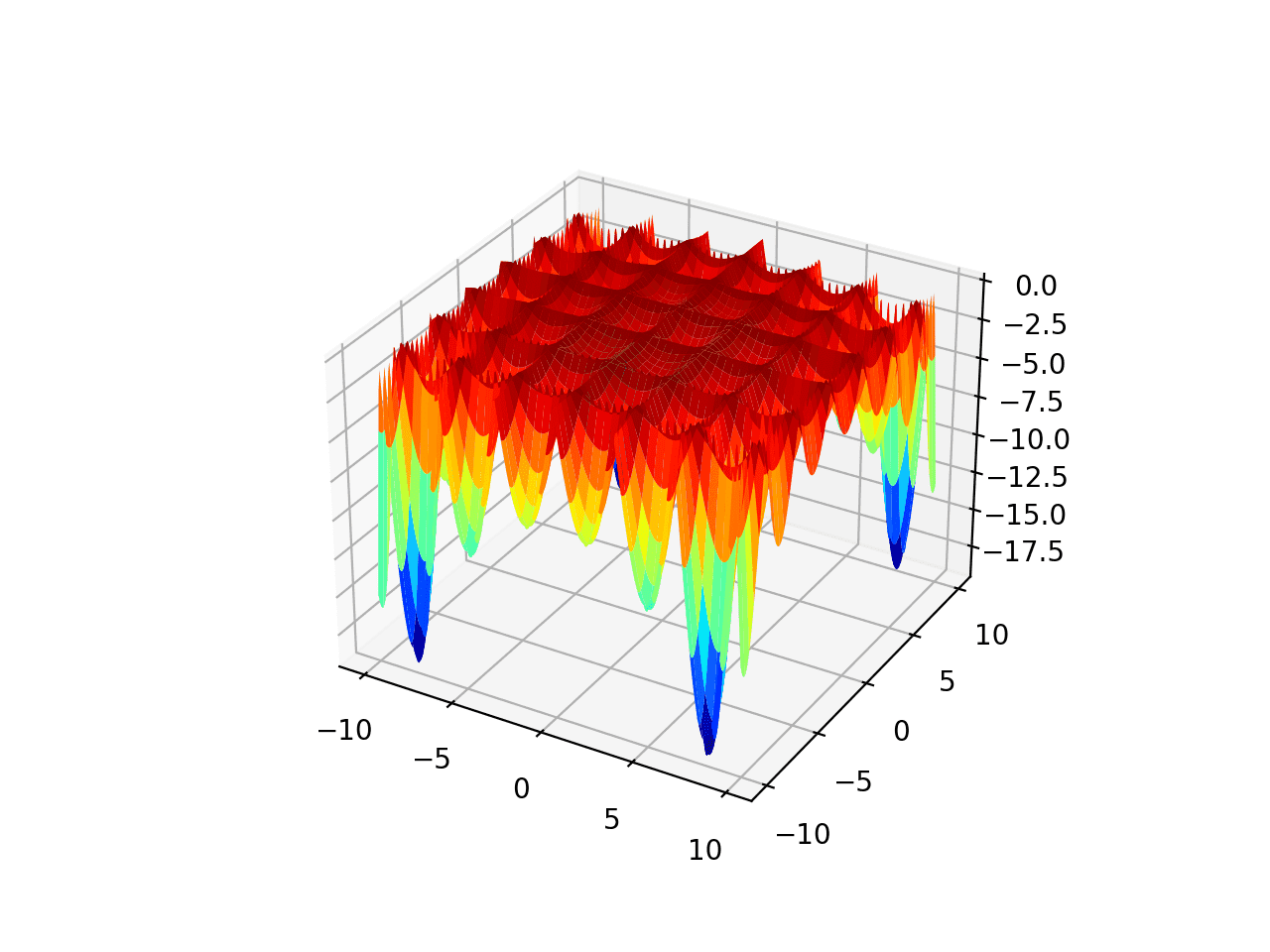
Диапазон ограничен промежутком [-10,0 и 10,0] и функцией с четырьмя глобальными оптимумами в точках [8,05502, 9,66459], [-8,05502, 9,66459], [8,05502, -9,66459], [-8,05502, -9,66459]. Эта функция известна как табличная функция Хольдера.
# multimodal test function from numpy import arange from numpy import exp from numpy import sqrt from numpy import cos from numpy import sin from numpy import e from numpy import pi from numpy import absolute from numpy import meshgrid from matplotlib import pyplot from mpl_toolkits.mplot3d import Axes3D # objective function def objective(x, y): return -absolute(sin(x) * cos(y) * exp(absolute(1 - (sqrt(x**2 + y**2)/pi)))) # define range for input r_min, r_max = -10.0, 10.0 # sample input range uniformly at 0.1 increments xaxis = arange(r_min, r_max, 0.1) yaxis = arange(r_min, r_max, 0.1) # create a mesh from the axis x, y = meshgrid(xaxis, yaxis) # compute targets results = objective(x, y) # create a surface plot with the jet color scheme figure = pyplot.figure() axis = figure.gca(projection='3d') axis.plot_surface(x, y, results, cmap='jet') # show the plot pyplot.show()Код создаёт поверхность согласно графику функции.
Резюме
Если вы хотите глубже погрузиться в тему — обратите внимание на сопутствующие материалы ниже.

Узнайте, как прокачаться в других специальностях или освоить их с нуля:
Другие профессии и курсы
ПРОФЕССИИ
КУРСЫ
ссылка на оригинал статьи https://habr.com/ru/company/skillfactory/blog/549472/
Добавить комментарий