Виртуальных частиц не существует

И бесконечного количества пар «частица-античастица» в вакууме тоже нет.

Выражение «виртуальная частица» часто попадается в физике и в научно-популярных объяснениях квантовой теории поля. Но на самом деле виртуальных частиц как таковых не существует. Сегодня мы поговорим о том, зачем (и в каком виде) нужны виртуальные частицы, и почему их не существует. 

Квантовая теория поля

Наша история начинается с квантовой теории поля.

Выше схематично показано поле Хиггса. Его можно трактовать так: каждой точке в пространстве и времени мы присваиваем случайное свойство. Это может быть число, вектор, тензор, что хотите. Затем пытаемся понять, как это свойство изменяется с течением времени и при взаимодействии с другими сущностями. Вот вся суть теории поля.

В квантовой теории мы первым делом присваиваем поле каждой точке в пространстве. Это поле может быть описано простыми числами, которые называются скалярами, а может быть описано и более сложными сущностями – векторами.

Если в квантовой теории поля сообщить полю некоторую энергию, то поле изменяется: оно начинает колебаться между конкретными значениями. Такое колебание (осцилляция) напоминает частицу.

Если такая картинка кажется вам слишком обобщенной – ничего страшного, много деталей нам и не нужно. Достаточно помнить, что существуют поля, а осцилляции таких полей – это частицы.

Диаграммы Фейнмана, и как отображаются взаимодействия на них

Выше показана обычная диаграмма Фейнмана. Такая схема описывает взаимодействия между двумя или более частицами.

Например, на вышеприведенной диаграмме показано, как отталкиваются два электрона. Как известно, одинаковые заряды отталкиваются под действием электромагнитной силы, но на самом деле все несколько тоньше. Когда два электрона слишком приближаются друг к другу, они обмениваются фотоном: частицей света.

Этот процесс можно с тем же успехом описать и следующим образом, но такая трактовка будет немного строже (можете ее пропустить, если вам не нравится разбираться в полях): два источника осцилляций в поле электронов слишком сближаются, настолько, что немного перекрывают друг друга.

В результате возникают осцилляции в другом поле: электромагнитном. Из-за электромагнитных осцилляций две осцилляции электронного поля отдаляются друг от друга.

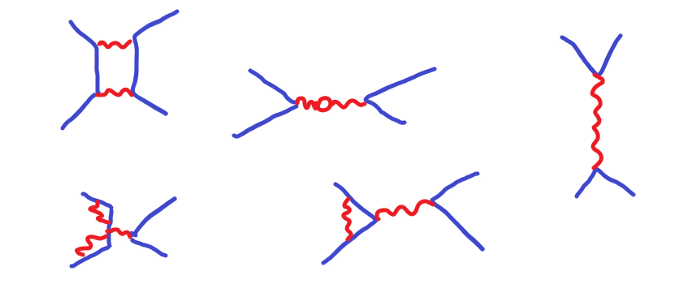
Небольшая загвоздка, которая просматривается в вышеприведенных диаграммах – есть множество вариантов взаимного отталкивания для двух электронов. Мы не будем вдаваться в специфику всевозможных диаграмм Фейнмана, это тема для отдельной статьи.

А следующий пункт давайте разберем внимательнее и докопаемся до некоторых деталей.

Теория возмущений

Представьте, что вам нужно решить алгебраическую задачу. Вам известна формула (x +a)² = x² + 2ax + a². Но задача сложнее. Что же делать? Вы попытаетесь решить задачу при помощи формулы, которую знаете. Если это не сработает, то вы попытаетесь выкрутиться при помощи сложения и вычитания, а затем применить формулу.

Примерно так и работает теория возмущений. Нам нужно каким-то образом решать задачи, которые слишком сложны; например, описывая такие взаимодействия, как показаны выше.

Может показаться, а что сложного в двух отталкивающихся электронах; но это взаимодействие связано со множеством сложных (и довольно запутанных) расчетов. Итак, чтобы было легче, возьмем очень простой случай (весьма, весьма далекий от того, что происходит на самом деле – как самая первая диаграмма Фейнмана из этой статьи) и посчитаем.

Затем разберем чуть более сложный случай (сложнее первого, но все равно очень далекий от реальности) и посчитаем его. Возьмем результаты двух приблизительных вычислений, а затем суммируем их, чтобы получить другое хорошее приближение.

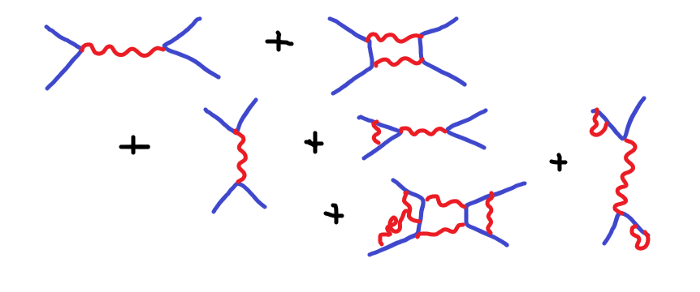
Может показаться, что на этой картинке мы складываем диаграммы, но на самом деле – нет; мы складываем интегральные уравнения, представленные этими диаграммами.

В каждом из этих приближений содержатся различные конфигурации электромагнитного поля (того, что порождает фотон). Эти конфигурации соответствуют различным осцилляциям поля, но, при сложении осцилляций, с большой точностью воспроизводится то, что действительно происходит в реальности.  

Виртуальные частицы

Держим в уме, что различные осцилляции, аппроксимирующие реальность – это просто придуманные нами ухищрения, призванные найти более простые решения для стоящей перед нами задачи. На самом деле этих осцилляций не существует. Если хотите, это «формальные» осцилляции, математический трюк.

Для них прижилось название «виртуальные частицы». Считается, что они «возникают и сразу исчезают», но «на настолько краткое время, что можно не считать их реальными».

Да, осциллирующие поля ассоциированы с частицами, но эти осцилляции (и, следовательно, соответствующие частицы) не существуют. Они изобретены, чтобы упростить довольно сложную (реальную) осцилляцию. Они вообще не существуют, в течение даже кратчайших интервалов времени.

Принцип неопределенности Гейзенберга

Возможно, ранее вам уже встречалась эта формула:

Это знаменитый Принцип неопределенности Гейзенберга: в любой момент невозможно узнать для конкретного поля и энергию, и время. Именно поэтому и появилась концепция виртуальных частиц: поскольку при сколь угодно малых значениях времени энергию узнать невозможно, поле должно «бурлить» от виртуальных частиц.

Притом, что я не отрицаю справедливости принципа Гейзенберга, он никоим образом не свидетельствует о существовании виртуальных частиц. Согласно этому принципу, в вакууме существует небольшая неопределенность относительно того, какова может быть энергия поля. И все.  

Если резюмировать: нам точно не известно, какова именно энергия поля в очень малые промежутки времени. От пикосекунды к пикосекунде эта энергия может колебаться, и не существует способа совершенно точно измерить и спрогнозировать энергию любого поля.  Вот стандартная модель и полный список реально существующих частиц:

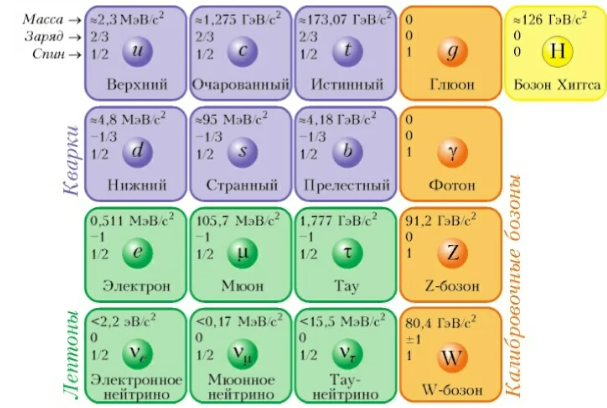
Разумеется, не исключено, что в будущем будет найдено и множество новых частиц, но пока, как с теоретической, так и с экспериментальной точки зрения  могут существовать только эти частицы. Нереальные частицы из пустоты? Это научная фантастика или математика.

Откуда весь сыр-бор?

Может показаться, что теоретизировать о виртуальных частицах неправильно. Нет, это не так.

Виртуальные частицы полезны: они упрощают нам математику, помогают наглядно представить теорию возмущений, могут использоваться для новых прогнозов и помочь открыть новую физику. Да, это удобный и полезный конструкт, никаких сомнений.

Но важно различать, где математика, а где реальность. Возьмем, к примеру, Хокинговское излучение.

Считается, что хокинговское излучение возникает при образовании пары виртуальных частиц, когда одна из этих частиц падает в черную дыру, а другой удается ускользнуть. Наглядно и понятно.

Строго говоря, Хокинговское излучение никак не связано с виртуальными частицами. Оно связано с осцилляциями, о которых шла речь выше, и с тем, как их видят разные люди, расположенные кто ближе, кто дальше от черной дыры.

Притом, что виртуальные частицы помогают понять феномен, это отнюдь не означает, что они дают полную картину. Хокинговское излучение – один из тех феноменов, где математика воспринимается практически буквально, чтобы упростить описание явления.

Что же в этом плохого? Пока мои методы позволяют мне приходить к верным результатам, я вправе упрощать, верно?

Да, верно. Пока мы не путаем реальность с математическими упрощениями и четко понимаем, какова реальная картина. Именно об этом и была статья.  

Думаю заключить ее словами Фейнмана:

Главный принцип – не дурачить самого себя. А себя как раз легче всего одурачить.