
Многие знают правила этой головоломки (Skyscrapers):
Перед вами вид сверху на городской квартал. В каждой клетке стоит «небоскреб» высотой, равной числу в этой клетке. Числа с боков сетки означают количество «небоскребов», видимых из соответствующей строки или столбца, если смотреть от этого числа.
Задача: заполнить сетку числами так, чтобы в каждой строке и в каждом столбце каждое число использовалось лишь единожды.
Понятно, что алгоритмом полного перебора можно решить что угодно, но — за экспоненциальное время. Поэтому мы попробуем написать такой SQL-запрос, который решит нам такую головоломку за приемлемое время.
Зачем же делать это на SQL? Потому что можем! А заодно потому что это позволит научиться конструировать «очень сложные запросы», что может пригодиться и в обычной работе.
Возьмем реальный пример
Любой хоть сколько-то сложный SQL-запрос лучше всего конструируется на конкретном примере. Давайте возьмем для него с сайта playsudoku.ru один из «сложных» вариантов этой головоломки в размере 9×9:

TL; DR — не заглядывайте без подготовки!
WITH RECURSIVE src AS ( SELECT x - 1 x , y - 1 y , nullif(n, '.')::integer n FROM (VALUES( -- http://www.playsudoku.ru/skyscrapers/sky_9_3_01.html $$ . 4 . 3 3 2 1 3 5 2 . . . 2 . . . . . . . 3 3 . . . . . . . . . 1 3 2 . 6 . 7 . 4 . . 3 2 . . 1 . . . 6 . 7 2 3 . . . 4 . 7 . . . 4 2 3 . 2 . . . 5 . . 2 1 . . 5 . 6 . 2 . 4 3 4 . . . . . . . . . . 4 . . . . . . . 7 . 3 . 3 3 2 3 4 6 1 2 5 . $$ )) T(s) , LATERAL regexp_split_to_table(regexp_replace(s, '(^\n|\n$)', '', 'g'), '\n+') WITH ORDINALITY AS L(line, y) , LATERAL regexp_split_to_table(line, '\s+') WITH ORDINALITY AS C(n, x) ) -- формируем "боковые" ограничения , side AS ( SELECT m - 1 m , Y.* FROM ( SELECT max(x) m FROM src ) X , LATERAL ( SELECT array_agg(n ORDER BY x) FILTER(WHERE y = 0 AND x > 0 AND x < m) u , array_agg(n ORDER BY x) FILTER(WHERE y = m AND x > 0 AND x < m) d , array_agg(n ORDER BY y) FILTER(WHERE x = 0 AND y > 0 AND y < m) l , array_agg(n ORDER BY y) FILTER(WHERE x = m AND y > 0 AND y < m) r FROM src ) Y ) -- собираем фиксированные разрешения , fix AS ( SELECT x , y , array_agg(n) FILTER( WHERE coalesce( -- защита от незаданного бокового ограничения NOT( -- единичка на стороне => максимум в соседней ячейке (l[y] = 1 AND x = 1 AND n < m) OR (r[y] = 1 AND x = m AND n < m) OR (u[x] = 1 AND y = 1 AND n < m) OR (d[x] = 1 AND y = m AND n < m) OR -- расстояние до "борта" l[y] + n > m + x OR u[x] + n > m + y OR r[y] + n > m + (m - x + 1) OR d[x] + n > m + (m - y + 1) ) , TRUE ) ) cell FROM side , LATERAL generate_series(1, m) x -- "цикл" по X , LATERAL generate_series(1, m) y -- "цикл" по Y , LATERAL generate_series(1, m) n -- "цикл" по значениям GROUP BY x, y ) , base AS ( SELECT x , y , CASE WHEN n IS NOT NULL THEN ARRAY[n] -- подставляем фиксированные значения ELSE cell END cell FROM fix NATURAL LEFT JOIN src ORDER BY x, y ) , rec_03 AS ( SELECT '{}'::json[] fixpath , json_agg(row_to_json(T)) matrix , NULL::json result , TRUE has_many , FALSE has_none FROM base T UNION ALL ( WITH mv AS ( TABLE rec_03 ) ( -- вычисление результата "вычеркиваний" SELECT mv.fixpath , mv.matrix , T.result , T.has_many , T.has_none FROM mv , LATERAL ( WITH RECURSIVE unpack AS ( SELECT * FROM json_to_recordset(coalesce(result, matrix)) unpack(x bigint, y bigint, cell bigint[]) ) , rec_02 AS ( SELECT 0 lvl , * FROM unpack UNION ALL -- "вычеркивание" значений ( WITH RECURSIVE mv AS ( TABLE rec_02 ) , rec_01 AS ( TABLE mv UNION ALL ( WITH mv AS ( TABLE rec_01 ) , step0 AS ( SELECT * , cell cell_new FROM mv WHERE NOT EXISTS( SELECT NULL FROM mv WHERE cell = '{}' ) ) -- ограничение по столбцу/строке от зафиксированных значений , heur_a AS ( SELECT x , y , array_agg(DISTINCT cell_new[1]) cell_cross FROM step0 WHERE array_length(cell, 1) = 1 -- единственное значение в точке GROUP BY GROUPING SETS((x), (y)) -- группируем одновременно в двух разрезах ) , step1 AS ( SELECT lvl , s.x , s.y , cell , CASE -- вычисляем новое значение только для незафиксированных ячеек WHEN array_length(cell_new, 1) > 1 THEN ARRAY( -- разность множеств SELECT unnest(s.cell) EXCEPT SELECT unnest(hx.cell_cross) EXCEPT SELECT unnest(hy.cell_cross) ) ELSE cell_new END cell_new FROM step0 s LEFT JOIN heur_a hx ON hx.x = s.x LEFT JOIN heur_a hy ON hy.y = s.y ) -- единственная доступная позиция для значения - нужная , heur_b AS ( SELECT DISTINCT s.x , s.y , ARRAY[n] cell_single FROM ( SELECT * FROM step1 WHERE array_length(cell_new, 1) > 1 ) s JOIN ( SELECT x , y , unnest(cell_new) n FROM step1 GROUP BY GROUPING SETS((n, x), (n, y)) -- группируем по значению и строке/столбцу HAVING count(*) = 1 -- единственность позиции значения в группе ) T ON n = ANY(cell_new) AND (T.x = s.x OR T.y = s.y) ) , step2 AS ( SELECT lvl , x , y , cell , coalesce(cell_single, cell_new) cell_new FROM step1 NATURAL LEFT JOIN heur_b ) SELECT lvl + 1 , x , y , cell_new cell FROM step2 WHERE -- итерируем, пока хоть что-то "вычеркивается" EXISTS( SELECT NULL FROM step2 WHERE array_length(cell_new, 1) < array_length(cell, 1) ) ) ) -- последний шаг рекурсии , step3 AS ( SELECT * FROM rec_01 WHERE lvl = (SELECT max(lvl) FROM rec_01) ) -- ограничение видимости по столбцам , heur_cx AS ( -- генерируем всевозможные комбинации без повторов WITH RECURSIVE gen AS ( SELECT generate_series(1, m) x , 0::bigint y , '{}'::bigint[] comb FROM side UNION ALL SELECT s.x , s.y , comb || n FROM gen JOIN step3 s ON (s.x, s.y) = (gen.x, gen.y + 1) JOIN LATERAL unnest(cell) n ON n <> ALL(comb) -- запрет повтора значения ) SELECT gen.x , ord.y , array_agg(DISTINCT n) cell_y FROM side JOIN gen ON array_length(comb, 1) = m -- оставляем только итоговые комбинации полного размера JOIN LATERAL ( -- вычисление по массиву значений "видимости" SELECT sum((comb[n] > ALL(comb[:n-1]))::integer) vu , sum((comb[n] > ALL(comb[n+1:]))::integer) vd FROM generate_series(1, m) n ) T ON (vu, vd) = (coalesce(u[x], vu), coalesce(d[x], vd)) -- оставляем только подходящие , LATERAL unnest(comb) WITH ORDINALITY ord(n, y) GROUP BY 1, 2 ) -- ограничение видимости по строкам , heur_cy AS ( WITH RECURSIVE gen AS ( SELECT 0::bigint x , generate_series(1, m) y , '{}'::bigint[] comb FROM side UNION ALL SELECT s.x , s.y , comb || n FROM gen JOIN step3 s ON (s.x, s.y) = (gen.x + 1, gen.y) JOIN LATERAL unnest(cell) n ON n <> ALL(comb) ) SELECT ord.x , gen.y , array_agg(DISTINCT n) cell_x FROM side JOIN gen ON array_length(comb, 1) = m JOIN LATERAL ( SELECT sum((comb[n] > ALL(comb[:n-1]))::integer) vl , sum((comb[n] > ALL(comb[n+1:]))::integer) vr FROM generate_series(1, m) n ) T ON (vl, vr) = (coalesce(l[y], vl), coalesce(r[y], vr)) , LATERAL unnest(comb) WITH ORDINALITY ord(n, x) GROUP BY 1, 2 ) , step4 AS ( SELECT lvl , x , y , cell -- значения должны удовлетворять условиям и по строке, и по столбцу , ARRAY( SELECT unnest(cell) INTERSECT SELECT unnest(cell_x) INTERSECT SELECT unnest(cell_y) ) cell_new FROM step3 NATURAL LEFT JOIN heur_cx NATURAL LEFT JOIN heur_cy ) SELECT lvl + 1 , x , y , cell_new cell FROM step4 WHERE EXISTS( SELECT NULL FROM step4 s JOIN mv USING(x, y) WHERE array_length(s.cell_new, 1) < array_length(mv.cell, 1) ) ) ) , last_iter AS ( SELECT x , y , cell FROM rec_02 WHERE lvl = (SELECT max(lvl) FROM rec_02) AND lvl > 0 ) SELECT coalesce(json_agg(row_to_json(T)), '[]') result , bool_or(array_length(cell, 1) > 1) has_many -- есть ячейки с несколькими значениями , bool_or(coalesce(cell, '{}') = '{}') has_none -- есть пустые ячейки FROM last_iter T ) T WHERE -- нечетный шаг mv.result IS NULL UNION ALL -- фиксация значений ячейки SELECT T.fixpath , T.matrix , NULL , mv.has_many , mv.has_none FROM mv , LATERAL ( WITH unpack AS ( SELECT * FROM json_to_recordset(coalesce(result, matrix)) unpack(x bigint, y bigint, cell bigint[]) ) SELECT -- добавляем фиксируемую ячейку к json[] и превращаем в '[]'::json to_json(matrix_flt || vn) matrix , fixpath || vn fixpath FROM -- определяем фиксируемую ячейку ( SELECT * FROM unpack WHERE array_length(cell, 1) > 1 ORDER BY array_length(cell, 1), x, y LIMIT 1 ) fix -- собираем отфильтрованный json без этой ячейки , LATERAL ( SELECT array_agg(row_to_json(T)) FILTER(WHERE (x, y) <> (fix.x, fix.y)) matrix_flt FROM unpack T ) T0 -- организуем перебор вариантов значений , LATERAL unnest(cell) n -- формируем json-представление этой ячейки с конкретным значением , LATERAL ( SELECT row_to_json(T) vn FROM ( SELECT x , y , ARRAY[n] cell ) T ) T1 ) T WHERE -- четный шаг mv.result IS NOT NULL AND -- пока нет пустых ячеек, но есть незафиксированные mv.has_many AND NOT mv.has_none ) ) ) -- находим и распаковываем запись с решением , unpack AS ( SELECT * FROM json_to_recordset(( SELECT result FROM rec_03 WHERE NOT has_many AND -- нет вариативности NOT has_none -- нет занулений LIMIT 1 )) unpack(x bigint, y bigint, cell bigint[]) ) -- собираем в матрицу SELECT string_agg( lpad(cell[1]::text, (SELECT length(m::text) FROM side)) , ' ' ORDER BY x ) line FROM unpack GROUP BY y ORDER BY y;Из псевдоматрицы — в рекордсет
Как это можно представить в SQL? Давайте договоримся, что пустая клетка у нас будет обозначена точкой, а заполненная — стоящим в ней числом. Тогда всю матрицу можно представить как единое текстовое значение и разобрать на строки-столбцы с помощью пары регулярных выражений:
WITH src AS ( SELECT x - 1 x , y - 1 y , nullif(n, '.')::integer n FROM (VALUES( -- http://www.playsudoku.ru/skyscrapers/sky_9_3_01.html $$ . 4 . 3 3 2 1 3 5 2 . . . 2 . . . . . . . 3 3 . . . . . . . . . 1 3 2 . 6 . 7 . 4 . . 3 2 . . 1 . . . 6 . 7 2 3 . . . 4 . 7 . . . 4 2 3 . 2 . . . 5 . . 2 1 . . 5 . 6 . 2 . 4 3 4 . . . . . . . . . . 4 . . . . . . . 7 . 3 . 3 3 2 3 4 6 1 2 5 . $$ )) T(s) , LATERAL regexp_split_to_table(regexp_replace(s, '(^\n|\n$)', '', 'g'), '\n+') WITH ORDINALITY AS L(line, y) , LATERAL regexp_split_to_table(line, '\s+') WITH ORDINALITY AS C(n, x) )Получаем уже пронумерованный за счет использования WITH ORDINALITY рекордсет из 11 x 11 строк — внутренний квадрат 9 x 9, плюс значения «видимости» сверху-снизу и слева-справа:
x | y | n 0 | 0 | - 1 | 0 | 4 2 | 0 | - 3 | 0 | 3 4 | 0 | 3 5 | 0 | 2 6 | 0 | 1 7 | 0 | 3 8 | 0 | 5 9 | 0 | 2 10 | 0 | - 0 | 1 | - 1 | 1 | - 2 | 1 | 2 ...Поскольку мы «строим» заведомо достаточно сложный запрос, то использование CTE (Common Table Expression) вместо вложенных запросов — это именно та «фишка», которая сразу позволяет значительно упростить его «сборку».
Теперь из этого выделим массивы, которые будут хранить количество «видимых небоскребов» в каждой позиции каждой из 4 сторон квадрата:
-- формируем "боковые" ограничения , side AS ( SELECT m - 1 m , Y.* FROM ( SELECT max(x) m FROM src ) X , LATERAL ( SELECT array_agg(n ORDER BY x) FILTER(WHERE y = 0 AND x > 0 AND x < m) u , array_agg(n ORDER BY x) FILTER(WHERE y = m AND x > 0 AND x < m) d , array_agg(n ORDER BY y) FILTER(WHERE x = 0 AND y > 0 AND y < m) l , array_agg(n ORDER BY y) FILTER(WHERE x = m AND y > 0 AND y < m) r FROM src ) Y )Бонусом мы вычислили m — размер стороны нашего квадрата:
m | u | d | l | r 9 | {4,NULL,3,3,2,1,3,5,2} | {3,3,2,3,4,6,1,2,5} | {NULL,3,3,2,3,2,1,4,4} | {3,1,3,2,4,2,3,NULL,3}"В некоторых позициях оказался NULL, но нас это не должно смущать, поскольку мы действительно ничего не знаем о значениях в этих ячейках.
Базовые ограничения
Первое соображение достаточно простое: если на стороне стоит значение 1, то в соседней с ним ячейке может стоять только максимальное из возможных значений, то есть m, потому что иначе этот «самый высокий небоскреб» будет все равно «просвечивать» через любой другой и мы должны будем «увидеть» значение не меньше 2:

Второе ограничение чуть сложнее. Рассмотрим на примере квадрата со стороной 4, при каком значении «сбоку», какие «небоскребы» где стоять точно не могут:

Очевидно, что если мы видим максимальное для такого квадрата значение 4, то единственная допустимая комбинация: 1, 2, 3, 4. Если же значение 3, то не существует ни одной расстановки, где в первой клетке стояло бы 3, или 4 в любой из первых двух. Аналогично для 2 и значения 4 в первой ячейке.
Теперь выразим это на SQL:
-- собираем фиксированные разрешения , fix AS ( SELECT x , y , array_agg(n) FILTER( WHERE coalesce( -- защита от незаданного бокового ограничения NOT( -- единичка на стороне => максимум в соседней ячейке (l[y] = 1 AND x = 1 AND n < m) OR (r[y] = 1 AND x = m AND n < m) OR (u[x] = 1 AND y = 1 AND n < m) OR (d[x] = 1 AND y = m AND n < m) OR -- расстояние до "борта" l[y] + n > m + x OR u[x] + n > m + y OR r[y] + n > m + (m - x + 1) OR d[x] + n > m + (m - y + 1) ) , TRUE ) ) cell FROM side , LATERAL generate_series(1, m) x -- "цикл" по X , LATERAL generate_series(1, m) y -- "цикл" по Y , LATERAL generate_series(1, m) n -- "цикл" по значениям GROUP BY x, y )В результате, мы определили для каждой клетки набор значений, которые там вообще могут стоять:
x | y | cell 1 | 1 | {1,2,3,4,5,6} 1 | 2 | {1,2,3,4,5,6,7} 1 | 3 | {1,2,3,4,5,6,7} 1 | 4 | {1,2,3,4,5,6,7,8} 1 | 5 | {1,2,3,4,5,6,7} 1 | 6 | {1,2,3,4,5,6,7,8} 1 | 7 | {9} 1 | 8 | {1,2,3,4,5,6} 1 | 9 | {1,2,3,4,5,6}Теперь к этому мы легко добавляем исходно известные фиксированные позиции из самого квадрата, представив их в виде массива из единственного возможного значения:
, step0 AS ( SELECT x , y , CASE WHEN n IS NOT NULL THEN ARRAY[n] -- подставляем фиксированные значения ELSE cell END cell FROM fix NATURAL LEFT JOIN src ORDER BY x, y )x | y | cell 1 | 1 | {1,2,3,4,5,6} 1 | 2 | {1,2,3,4,5,6,7} 1 | 3 | {2} 1 | 4 | {1,2,3,4,5,6,7,8} 1 | 5 | {1,2,3,4,5,6,7} 1 | 6 | {3} 1 | 7 | {9} 1 | 8 | {1,2,3,4,5,6} 1 | 9 | {1,2,3,4,5,6}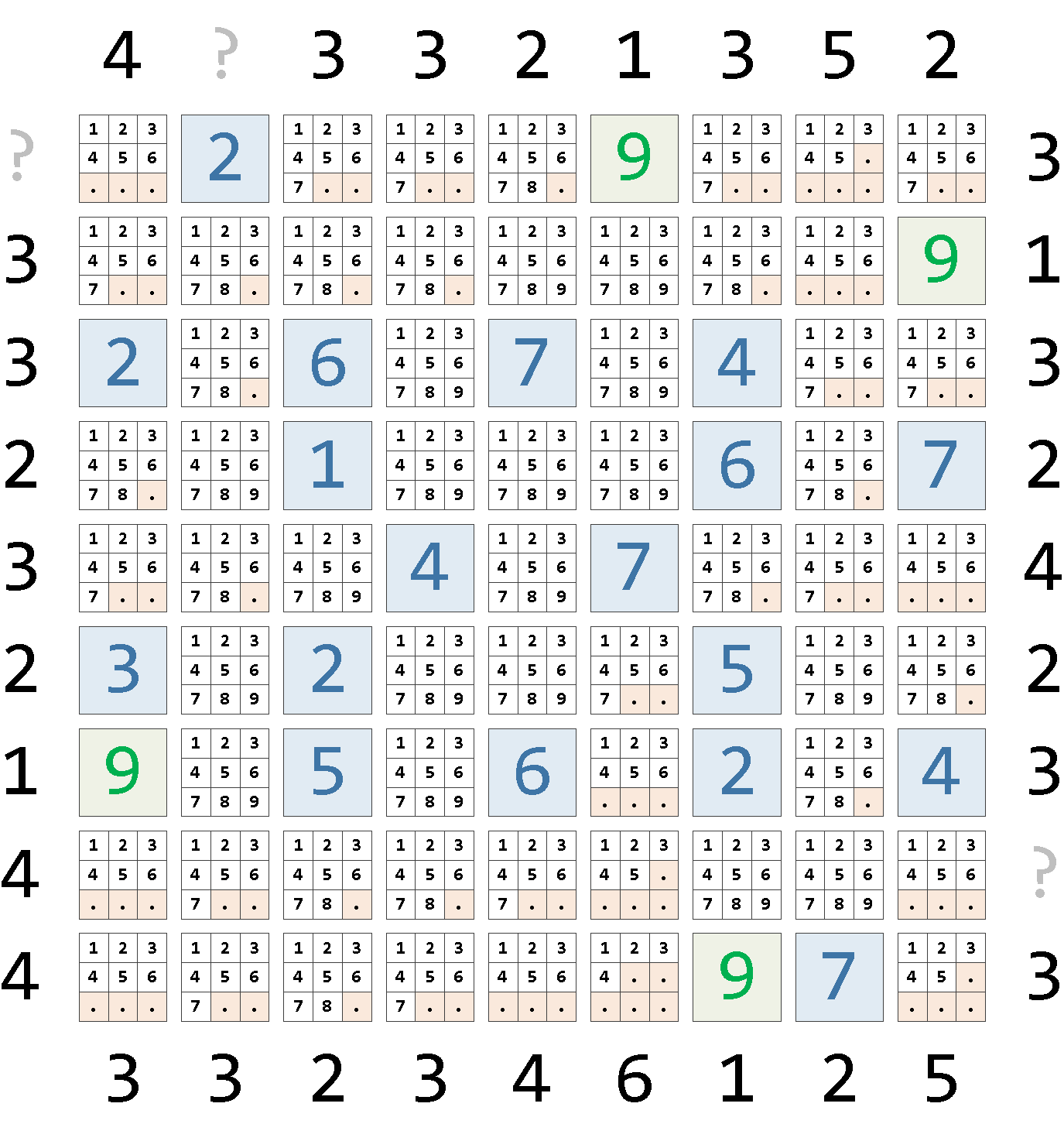
Это состояние станет «нулевым» шагом нашего алгоритма.
Эвристика «A»: ход ладьей
Теперь вспомним, что по условию задачи, все значения в каждой строке и каждом столбце различны. Это значит, что если мы уже достоверно определились, что в каких-то клетках находятся конкретные значения, то их не может быть больше нигде в этой же строке/столбце, и их можно «вычеркнуть».

-- ограничение по столбцу/строке от зафиксированных значений , heur_a AS ( SELECT x , y , array_agg(DISTINCT cell[1]) cell_cross FROM step0 WHERE array_length(cell, 1) = 1 -- единственное значение в точке GROUP BY GROUPING SETS((x), (y)) -- группируем одновременно в двух разрезах )x | y | cell_cross 1 | - | {2,3,9} 2 | - | {2} 3 | - | {1,2,5,6} 4 | - | {4} 5 | - | {6,7} 6 | - | {7,9} 7 | - | {2,4,5,6,9} 8 | - | {7} 9 | - | {4,7,9} - | 1 | {2,9} - | 2 | {9} - | 3 | {2,4,6,7} - | 4 | {1,6,7} - | 5 | {4,7} - | 6 | {2,3,5} - | 7 | {2,4,5,6,9} - | 9 | {7,9}, step1 AS ( SELECT s.x , s.y , cell , CASE -- вычисляем новое значение только для незафиксированных ячеек WHEN array_length(cell, 1) > 1 THEN ARRAY( -- разность множеств SELECT unnest(s.cell) EXCEPT SELECT unnest(hx.cell_cross) EXCEPT SELECT unnest(hy.cell_cross) ) ELSE cell END cell_new FROM step0 s LEFT JOIN heur_a hx ON hx.x = s.x LEFT JOIN heur_a hy ON hy.y = s.y )x | y | cell | cell_new 1 | 1 | {1,2,3,4,5,6} | {4,6,1,5} 1 | 2 | {1,2,3,4,5,6,7} | {4,6,7,1,5} 1 | 3 | {2} | {2} 1 | 4 | {1,2,3,4,5,6,7,8} | {4,5,8} 1 | 5 | {1,2,3,4,5,6,7} | {6,1,5} 1 | 6 | {3} | {3} 1 | 7 | {9} | {9} 1 | 8 | {1,2,3,4,5,6} | {4,6,1,5} 1 | 9 | {1,2,3,4,5,6} | {4,6,1,5} ...Здесь мы использовали достаточно распространенную в PostgreSQL технику вычисления операций над массивами как множествами в силу отсутствия таких встроенных функций:
-- объединение arraySetA + arraySetB = ARRAY( SELECT unnest(arraySetA) UNION SELECT unnest(arraySetB) ) -- исключение arraySetA - arraySetB = ARRAY(... EXCEPT ...) -- пересечение arraySetA * arraySetB = ARRAY(... INTERSECT ...)Посмотрим, что получилось:
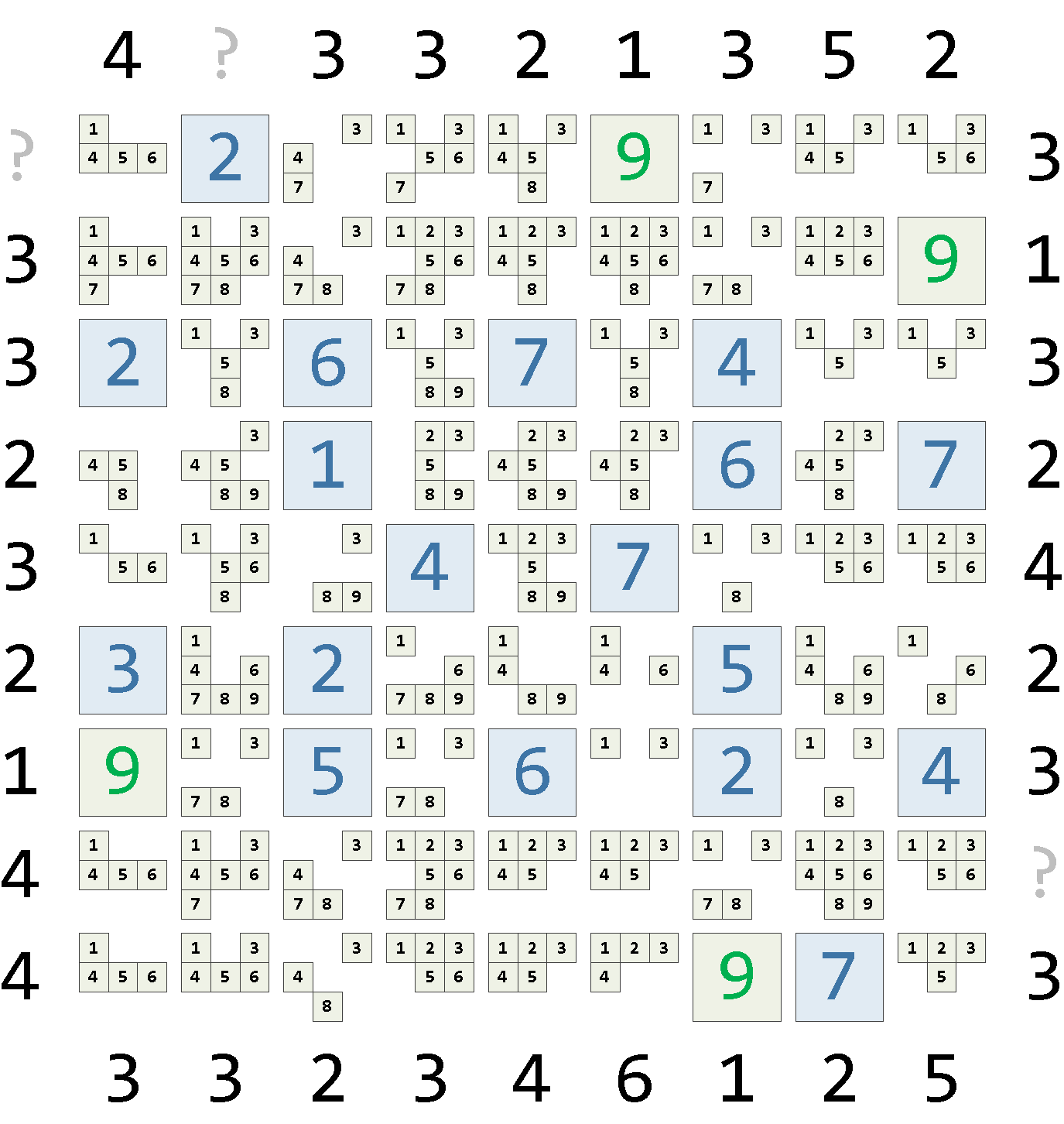
Эвристика «B»: один в поле не воин
Обратим внимание на первую же строку:

Из всех оставшихся комбинаций лишь в одной незафиксированной ячейке может находиться значение 8. А, раз по условию задачи, все значения в строке/столбце различны — значит, именно там оно и находится.
В коде это будет выглядеть так:
-- единственная доступная позиция для значения - нужная , heur_b AS ( SELECT DISTINCT s.x , s.y , ARRAY[n] cell_single FROM ( SELECT * FROM step1 WHERE array_length(cell_new, 1) > 1 ) s JOIN ( SELECT x , y , unnest(cell_new) n FROM step1 GROUP BY GROUPING SETS((n, x), (n, y)) -- группируем по значению и строке/столбцу HAVING count(*) = 1 -- единственность позиции значения в группе ) T ON n = ANY(cell_new) AND (T.x = s.x OR T.y = s.y) )За основу мы берем уже не исходное значение cell, а cell_new, полученное на предыдущем шаге алгоритма.
x | y | cell_single 1 | 2 | {7} 1 | 4 | {8} 3 | 5 | {9} 3 | 9 | {8} 4 | 3 | {9} 5 | 1 | {8} 8 | 8 | {9} 9 | 6 | {8}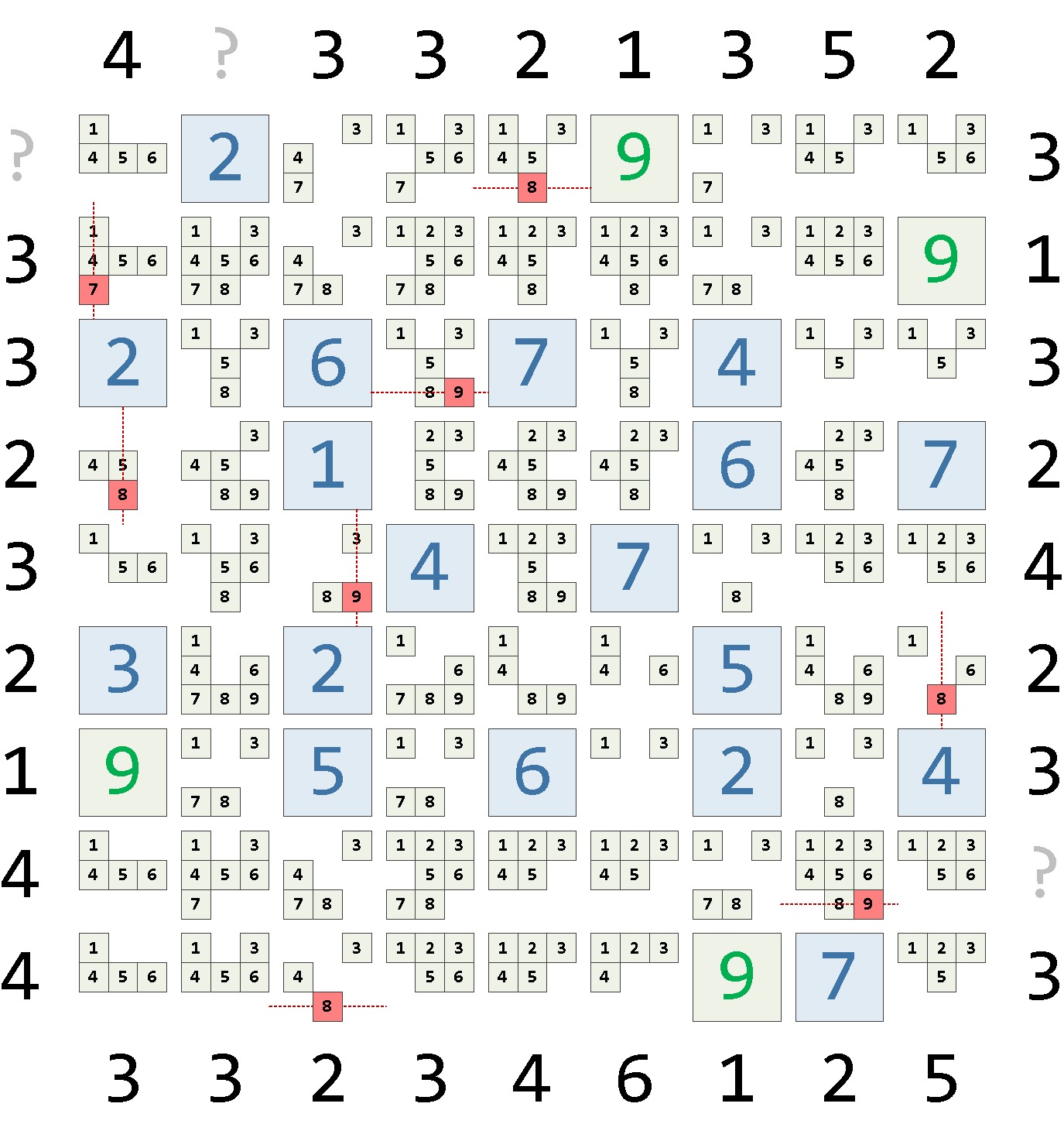
, step2 AS ( SELECT x , y , cell , coalesce(cell_single, cell_new) cell_new FROM step1 NATURAL LEFT JOIN heur_b )После наложения ограничений получаем:
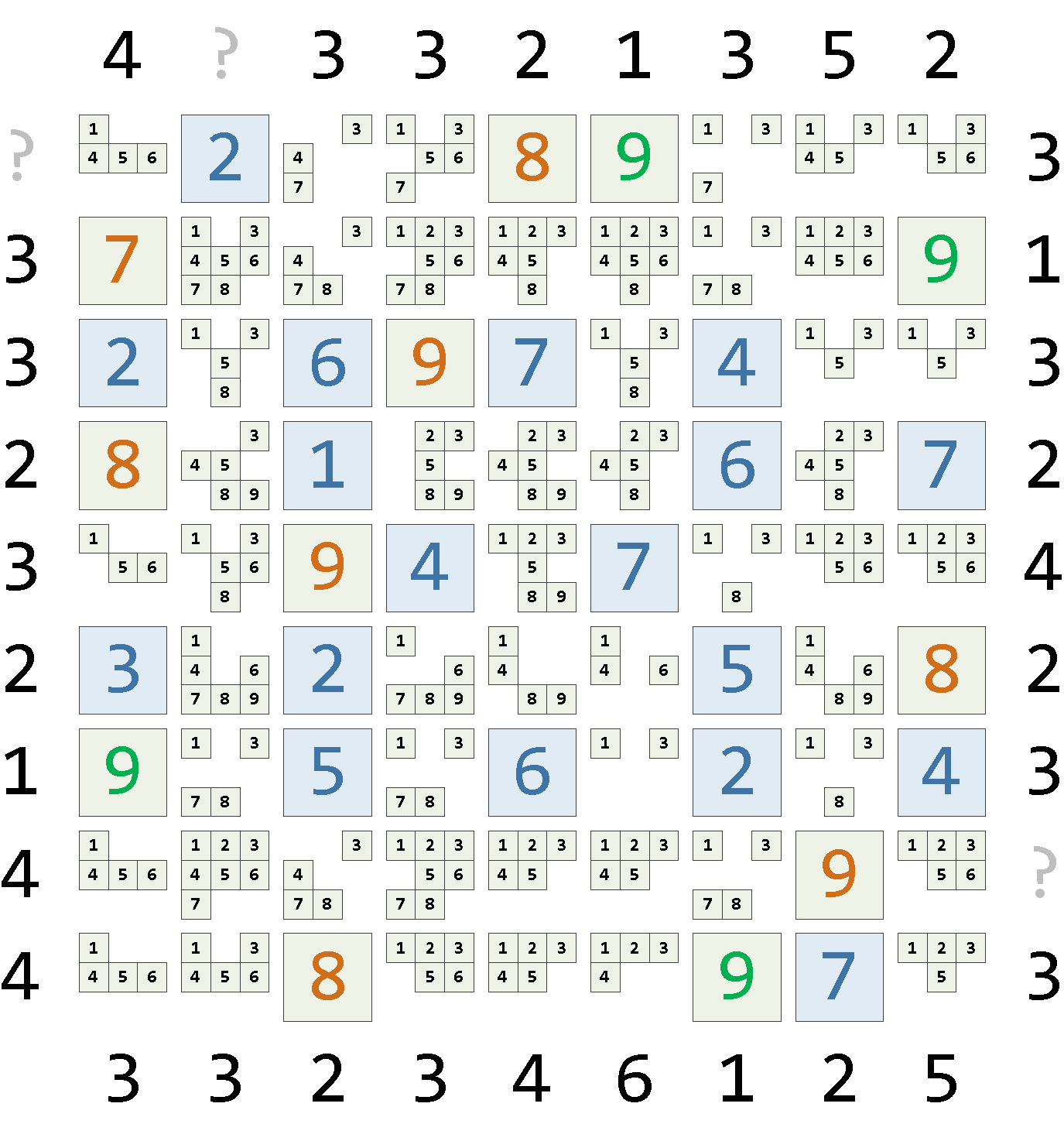
Организуем рекурсивные циклы
Теперь самое время заметить, что часть определенных на втором шаге значений позволяет снова «вычеркнуть» часть комбинаций точно так же, как мы сделали это на первом шаге (если значение было единственным по строке, то его можно убрать из столбца и наоборот), а потом опять поискать «единственные», и снова, и опять… — то есть нам нужен цикл! А на SQL циклы организуются с помощью рекурсивных запросов.
Самое главное в таких запросах — правильно подобрать условие выхода из рекурсии. Подробно я останавливался на этой теме в статьях «PostgreSQL Antipatterns: «Бесконечность — не предел!», или Немного о рекурсии» и «SQL HowTo: ломаем мозг об дерево — упорядочиваем иерархию с рекурсией и без».
Для данной задачи нам понадобится использование техник нумерации уровня рекурсии и «материализации» рекурсивной части выборки, чтобы к ней можно было обращаться неоднократно. Модифицируем наш запрос:
WITH RECURSIVE src AS ( -- ... -- вместо step0 , base AS ( SELECT x , y , CASE WHEN n IS NOT NULL THEN ARRAY[n] -- подставляем фиксированные значения ELSE cell END cell FROM fix NATURAL LEFT JOIN src ORDER BY x, y ) -- рекурсивный цикл , rec AS ( SELECT 0 lvl , * FROM base UNION ALL ( WITH step0 AS ( SELECT * , cell cell_new FROM rec ) -- ... все те же heur_a, step1, heur_b, step2, только с "протаскиванием" lvl SELECT lvl + 1 , x , y , cell_new cell FROM step2 WHERE -- итерируем, пока хоть что-то "вычеркивается" EXISTS( SELECT NULL FROM step2 WHERE array_length(cell_new, 1) < array_length(cell, 1) ) ) )Полный текст запроса
WITH RECURSIVE src AS ( SELECT x - 1 x , y - 1 y , nullif(n, '.')::integer n FROM (VALUES( -- http://www.playsudoku.ru/skyscrapers/sky_9_3_01.html $$ . 4 . 3 3 2 1 3 5 2 . . . 2 . . . . . . . 3 3 . . . . . . . . . 1 3 2 . 6 . 7 . 4 . . 3 2 . . 1 . . . 6 . 7 2 3 . . . 4 . 7 . . . 4 2 3 . 2 . . . 5 . . 2 1 . . 5 . 6 . 2 . 4 3 4 . . . . . . . . . . 4 . . . . . . . 7 . 3 . 3 3 2 3 4 6 1 2 5 . $$ )) T(s) , LATERAL regexp_split_to_table(regexp_replace(s, '(^\n|\n$)', '', 'g'), '\n+') WITH ORDINALITY AS L(line, y) , LATERAL regexp_split_to_table(line, '\s+') WITH ORDINALITY AS C(n, x) ) -- формируем "боковые" ограничения , side AS ( SELECT m - 1 m , Y.* FROM ( SELECT max(x) m FROM src ) X , LATERAL ( SELECT array_agg(n ORDER BY x) FILTER(WHERE y = 0 AND x > 0 AND x < m) u , array_agg(n ORDER BY x) FILTER(WHERE y = m AND x > 0 AND x < m) d , array_agg(n ORDER BY y) FILTER(WHERE x = 0 AND y > 0 AND y < m) l , array_agg(n ORDER BY y) FILTER(WHERE x = m AND y > 0 AND y < m) r FROM src ) Y ) -- собираем фиксированные разрешения , fix AS ( SELECT x , y , array_agg(n) FILTER( WHERE coalesce( -- защита от незаданного бокового ограничения NOT( -- единичка на стороне => максимум в соседней ячейке (l[y] = 1 AND x = 1 AND n < m) OR (r[y] = 1 AND x = m AND n < m) OR (u[x] = 1 AND y = 1 AND n < m) OR (d[x] = 1 AND y = m AND n < m) OR -- расстояние до "борта" l[y] + n > m + x OR u[x] + n > m + y OR r[y] + n > m + (m - x + 1) OR d[x] + n > m + (m - y + 1) ) , TRUE ) ) cell FROM side , LATERAL generate_series(1, m) x -- "цикл" по X , LATERAL generate_series(1, m) y -- "цикл" по Y , LATERAL generate_series(1, m) n -- "цикл" по значениям GROUP BY x, y ) , base AS ( SELECT x , y , CASE WHEN n IS NOT NULL THEN ARRAY[n] -- подставляем фиксированные значения ELSE cell END cell FROM fix NATURAL LEFT JOIN src ORDER BY x, y ) -- рекурсивный цикл , rec AS ( SELECT 0 lvl , * FROM base UNION ALL ( WITH step0 AS ( SELECT * , cell cell_new FROM rec ) -- ограничение по столбцу/строке от зафиксированных значений , heur_a AS ( SELECT x , y , array_agg(DISTINCT cell_new[1]) cell_cross FROM step0 WHERE array_length(cell, 1) = 1 -- единственное значение в точке GROUP BY GROUPING SETS((x), (y)) -- группируем одновременно в двух разрезах ) , step1 AS ( SELECT lvl , s.x , s.y , cell , CASE -- вычисляем новое значение только для незафиксированных ячеек WHEN array_length(cell_new, 1) > 1 THEN ARRAY( -- разность множеств SELECT unnest(s.cell) EXCEPT SELECT unnest(hx.cell_cross) EXCEPT SELECT unnest(hy.cell_cross) ) ELSE cell_new END cell_new FROM step0 s LEFT JOIN heur_a hx ON hx.x = s.x LEFT JOIN heur_a hy ON hy.y = s.y ) -- единственная доступная позиция для значения - нужная , heur_b AS ( SELECT DISTINCT s.x , s.y , ARRAY[n] cell_single FROM ( SELECT * FROM step1 WHERE array_length(cell_new, 1) > 1 ) s JOIN ( SELECT x , y , unnest(cell_new) n FROM step1 GROUP BY GROUPING SETS((n, x), (n, y)) -- группируем по значению и строке/столбцу HAVING count(*) = 1 -- единственность позиции значения в группе ) T ON n = ANY(cell_new) AND (T.x = s.x OR T.y = s.y) ) , step2 AS ( SELECT lvl , x , y , cell , coalesce(cell_single, cell_new) cell_new FROM step1 NATURAL LEFT JOIN heur_b ) SELECT lvl + 1 , x , y , cell_new cell FROM step2 WHERE -- итерируем, пока хоть что-то "вычеркивается" EXISTS( SELECT NULL FROM step2 WHERE array_length(cell_new, 1) < array_length(cell, 1) ) ) ) TABLE rec ORDER BY lvl DESC, x, y;После 3 таких итераций «вычеркивания» наша матрица примет такой вид:
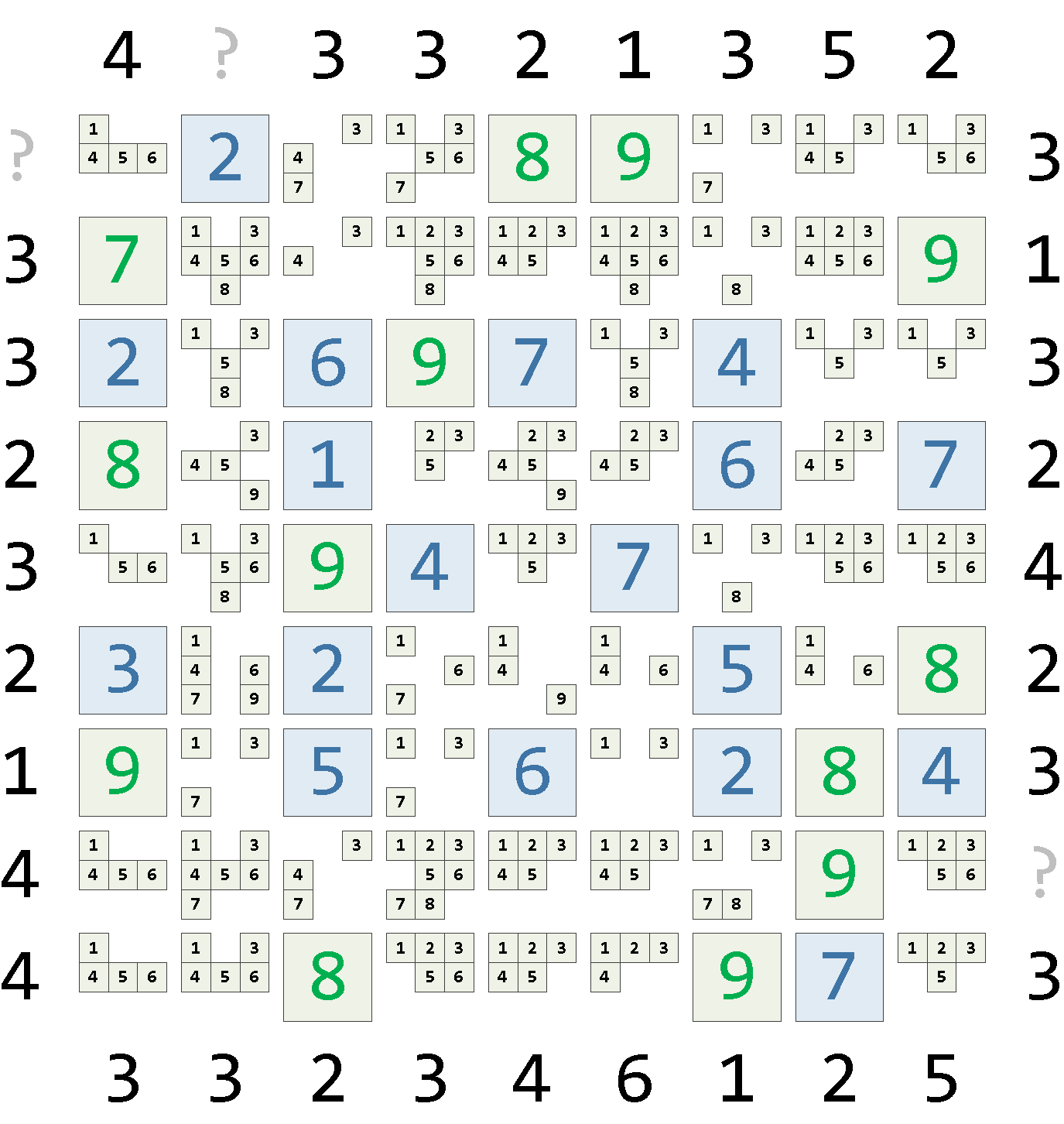
Можно заметить, что дополнительно у нас зафиксировалось в предпоследнем столбце значение 8, но дальше мы уперлись.
Эвристика «C»: посмотри по сторонам
Давайте взглянем внимательно на третью строку:

По условию единственности каждого значения в строке, мы можем получить следующие комбинации расстановок и результирующие значения «видимости»:
3 | 2 1 6 9 7 8 4 3 5 | 3 + 3 | 2 1 6 9 7 8 4 5 3 | 4 - 3 | 2 8 6 9 7 1 4 3 5 | 3 + 3 | 2 8 6 9 7 1 4 5 3 | 4 - 3 | 2 8 6 9 7 3 4 1 5 | 3 + 3 | 2 8 6 9 7 3 4 5 1 | 4 - 3 | 2 8 6 9 7 5 4 1 3 | 5 - 3 | 2 8 6 9 7 5 4 3 1 | 6 -Как видим, далеко не все расстановки удовлетворяют известным нам значениям 3 и 3. Давайте оставим только те, которые допустимы, и посмотрим, на каких перебираемых позициях какие значения возможны:
* * * * 2 1 6 9 7 8 4 3 5 2 8 6 9 7 1 4 3 5 2 8 6 9 7 3 4 1 5Оказывается, на первой такой позиции могут стоять только 1 и 8, но никак не 3 и 5, а на последней — наоборот, только 5:

Проведя аналогичный анализ по всем строкам и столбцам мы дополнительно сократим пространство возможных значений:
-- ограничение видимости по столбцам , heur_cx AS ( -- генерируем всевозможные комбинации без повторов WITH RECURSIVE gen AS ( SELECT generate_series(1, m) x , 0::bigint y , '{}'::bigint[] comb FROM side UNION ALL SELECT s.x , s.y , comb || n FROM gen JOIN step3 s ON (s.x, s.y) = (gen.x, gen.y + 1) JOIN LATERAL unnest(cell) n ON n <> ALL(comb) -- запрет повтора значения ) SELECT gen.x , ord.y , array_agg(DISTINCT n) cell_y FROM side JOIN gen ON array_length(comb, 1) = m -- оставляем только итоговые комбинации полного размера JOIN LATERAL ( -- вычисление по массиву значений "видимости" SELECT sum((comb[n] > ALL(comb[:n-1]))::integer) vu , sum((comb[n] > ALL(comb[n+1:]))::integer) vd FROM generate_series(1, m) n ) T ON (vu, vd) = (coalesce(u[x], vu), coalesce(d[x], vd)) -- оставляем только подходящие , LATERAL unnest(comb) WITH ORDINALITY ord(n, y) GROUP BY 1, 2 )Абсолютно симметрично то же самое проделываем для строк:
-- ограничение видимости по строкам , heur_cy AS ( WITH RECURSIVE gen AS ( SELECT 0::bigint x , generate_series(1, m) y , '{}'::bigint[] comb FROM side UNION ALL SELECT s.x , s.y , comb || n FROM gen JOIN step3 s ON (s.x, s.y) = (gen.x + 1, gen.y) JOIN LATERAL unnest(cell) n ON n <> ALL(comb) ) SELECT ord.x , gen.y , array_agg(DISTINCT n) cell_x FROM side JOIN gen ON array_length(comb, 1) = m JOIN LATERAL ( SELECT sum((comb[n] > ALL(comb[:n-1]))::integer) vl , sum((comb[n] > ALL(comb[n+1:]))::integer) vr FROM generate_series(1, m) n ) T ON (vl, vr) = (coalesce(l[y], vl), coalesce(r[y], vr)) , LATERAL unnest(comb) WITH ORDINALITY ord(n, x) GROUP BY 1, 2 ), step4 AS ( SELECT x , y , cell -- значения должны удовлетворять условиям и по строке, и по столбцу , ARRAY( SELECT unnest(cell) INTERSECT SELECT unnest(cell_x) INTERSECT SELECT unnest(cell_y) ) cell_new FROM step3 NATURAL LEFT JOIN heur_cx NATURAL LEFT JOIN heur_cy )
Ну, а теперь снова хочется «повычеркивать» и поискать единственные…
Можно бы и в первый рекурсивный блок включить применение этого ограничения, но тогда оно будет применяться на каждом шаге рекурсии, а не только когда уже все вычеркнуто — значит, генерируемых комбинаций будет еще слишком много, что печально скажется на времени выполнения запроса.
Поэтому по использованной выше методике «обрекурсивливания» заворачиваем запросы один в другой:
-- ... , rec_02 AS ( SELECT 0 lvl , * FROM base UNION ALL ( WITH RECURSIVE rec_01 AS ( SELECT * FROM rec_02 UNION ALL ( WITH step0 AS ( SELECT * , cell cell_new FROM rec_01 ) -- ...Полный текст запроса
WITH RECURSIVE src AS ( SELECT x - 1 x , y - 1 y , nullif(n, '.')::integer n FROM (VALUES( -- http://www.playsudoku.ru/skyscrapers/sky_9_3_01.html $$ . 4 . 3 3 2 1 3 5 2 . . . 2 . . . . . . . 3 3 . . . . . . . . . 1 3 2 . 6 . 7 . 4 . . 3 2 . . 1 . . . 6 . 7 2 3 . . . 4 . 7 . . . 4 2 3 . 2 . . . 5 . . 2 1 . . 5 . 6 . 2 . 4 3 4 . . . . . . . . . . 4 . . . . . . . 7 . 3 . 3 3 2 3 4 6 1 2 5 . $$ )) T(s) , LATERAL regexp_split_to_table(regexp_replace(s, '(^\n|\n$)', '', 'g'), '\n+') WITH ORDINALITY AS L(line, y) , LATERAL regexp_split_to_table(line, '\s+') WITH ORDINALITY AS C(n, x) ) -- формируем "боковые" ограничения , side AS ( SELECT m - 1 m , Y.* FROM ( SELECT max(x) m FROM src ) X , LATERAL ( SELECT array_agg(n ORDER BY x) FILTER(WHERE y = 0 AND x > 0 AND x < m) u , array_agg(n ORDER BY x) FILTER(WHERE y = m AND x > 0 AND x < m) d , array_agg(n ORDER BY y) FILTER(WHERE x = 0 AND y > 0 AND y < m) l , array_agg(n ORDER BY y) FILTER(WHERE x = m AND y > 0 AND y < m) r FROM src ) Y ) -- собираем фиксированные разрешения , fix AS ( SELECT x , y , array_agg(n) FILTER( WHERE coalesce( -- защита от незаданного бокового ограничения NOT( -- единичка на стороне => максимум в соседней ячейке (l[y] = 1 AND x = 1 AND n < m) OR (r[y] = 1 AND x = m AND n < m) OR (u[x] = 1 AND y = 1 AND n < m) OR (d[x] = 1 AND y = m AND n < m) OR -- расстояние до "борта" l[y] + n > m + x OR u[x] + n > m + y OR r[y] + n > m + (m - x + 1) OR d[x] + n > m + (m - y + 1) ) , TRUE ) ) cell FROM side , LATERAL generate_series(1, m) x -- "цикл" по X , LATERAL generate_series(1, m) y -- "цикл" по Y , LATERAL generate_series(1, m) n -- "цикл" по значениям GROUP BY x, y ) , base AS ( SELECT x , y , CASE WHEN n IS NOT NULL THEN ARRAY[n] -- подставляем фиксированные значения ELSE cell END cell FROM fix NATURAL LEFT JOIN src ORDER BY x, y ) , rec_02 AS ( SELECT 0 lvl , * FROM base UNION ALL ( WITH RECURSIVE rec_01 AS ( SELECT * FROM rec_02 UNION ALL ( WITH step0 AS ( SELECT * , cell cell_new FROM rec_01 ) -- ограничение по столбцу/строке от зафиксированных значений , heur_a AS ( SELECT x , y , array_agg(DISTINCT cell_new[1]) cell_cross FROM step0 WHERE array_length(cell, 1) = 1 -- единственное значение в точке GROUP BY GROUPING SETS((x), (y)) -- группируем одновременно в двух разрезах ) , step1 AS ( SELECT lvl , s.x , s.y , cell , CASE -- вычисляем новое значение только для незафиксированных ячеек WHEN array_length(cell_new, 1) > 1 THEN ARRAY( -- разность множеств SELECT unnest(s.cell) EXCEPT SELECT unnest(hx.cell_cross) EXCEPT SELECT unnest(hy.cell_cross) ) ELSE cell_new END cell_new FROM step0 s LEFT JOIN heur_a hx ON hx.x = s.x LEFT JOIN heur_a hy ON hy.y = s.y ) -- единственная доступная позиция для значения - нужная , heur_b AS ( SELECT DISTINCT s.x , s.y , ARRAY[n] cell_single FROM ( SELECT * FROM step1 WHERE array_length(cell_new, 1) > 1 ) s JOIN ( SELECT x , y , unnest(cell_new) n FROM step1 GROUP BY GROUPING SETS((n, x), (n, y)) -- группируем по значению и строке/столбцу HAVING count(*) = 1 -- единственность позиции значения в группе ) T ON n = ANY(cell_new) AND (T.x = s.x OR T.y = s.y) ) , step2 AS ( SELECT lvl , x , y , cell , coalesce(cell_single, cell_new) cell_new FROM step1 NATURAL LEFT JOIN heur_b ) SELECT lvl + 1 , x , y , cell_new cell FROM step2 WHERE -- итерируем, пока хоть что-то "вычеркивается" EXISTS( SELECT NULL FROM step2 WHERE array_length(cell_new, 1) < array_length(cell, 1) ) ) ) -- последний шаг рекурсии , step3 AS ( SELECT lvl , x , y , cell FROM rec_01 WHERE lvl = (SELECT max(lvl) FROM rec_01) ) -- ограничение видимости по столбцам , heur_cx AS ( -- генерируем всевозможные комбинации без повторов WITH RECURSIVE gen AS ( SELECT generate_series(1, m) x , 0::bigint y , '{}'::bigint[] comb FROM side UNION ALL SELECT s.x , s.y , comb || n FROM gen JOIN step3 s ON (s.x, s.y) = (gen.x, gen.y + 1) JOIN LATERAL unnest(cell) n ON n <> ALL(comb) -- запрет повтора значения ) SELECT gen.x , ord.y , array_agg(DISTINCT n) cell_y FROM side JOIN gen ON array_length(comb, 1) = m -- оставляем только итоговые комбинации полного размера JOIN LATERAL ( -- вычисление по массиву значений "видимости" SELECT sum((comb[n] > ALL(comb[:n-1]))::integer) vu , sum((comb[n] > ALL(comb[n+1:]))::integer) vd FROM generate_series(1, m) n ) T ON (vu, vd) = (coalesce(u[x], vu), coalesce(d[x], vd)) -- оставляем только подходящие , LATERAL unnest(comb) WITH ORDINALITY ord(n, y) GROUP BY 1, 2 ) -- ограничение видимости по строкам , heur_cy AS ( WITH RECURSIVE gen AS ( SELECT 0::bigint x , generate_series(1, m) y , '{}'::bigint[] comb FROM side UNION ALL SELECT s.x , s.y , comb || n FROM gen JOIN step3 s ON (s.x, s.y) = (gen.x + 1, gen.y) JOIN LATERAL unnest(cell) n ON n <> ALL(comb) ) SELECT ord.x , gen.y , array_agg(DISTINCT n) cell_x FROM side JOIN gen ON array_length(comb, 1) = m JOIN LATERAL ( SELECT sum((comb[n] > ALL(comb[:n-1]))::integer) vl , sum((comb[n] > ALL(comb[n+1:]))::integer) vr FROM generate_series(1, m) n ) T ON (vl, vr) = (coalesce(l[y], vl), coalesce(r[y], vr)) , LATERAL unnest(comb) WITH ORDINALITY ord(n, x) GROUP BY 1, 2 ) , step4 AS ( SELECT lvl , x , y , cell -- значения должны удовлетворять условиям и по строке, и по столбцу , ARRAY( SELECT unnest(cell) INTERSECT SELECT unnest(cell_x) INTERSECT SELECT unnest(cell_y) order by 1 ) cell_new FROM step3 NATURAL LEFT JOIN heur_cx NATURAL LEFT JOIN heur_cy ) SELECT lvl + 1 , x , y , cell_new cell FROM step4 WHERE EXISTS( SELECT NULL FROM step4 WHERE array_length(cell_new, 1) < array_length(cell, 1) ) ) ) TABLE rec_02 ORDER lvl DESC, x, y;
Да здравствует брутфорс!
Вот мы и пришли к ситуации, когда единственный возможный шаг — прямое моделирование с последующей проверкой условий. И таки да, в такую ситуацию мы можем попасть не раз, поэтому — снова рекурсия.
Чтобы не пришлось перебирать много, на каждом таком шаге мы возьмем самую первую ячейку, где меньше всего вариантов значений, и поочередно попробуем подставить каждое из них.
json_to_recordset
Но как передать целую матрицу между шагами рекурсии, да еще и с подменой значения в ячейке? Тут нам придут на помощь операции над json:
-- "упаковка" матрицы SELECT json_agg(row_to_json(T)) result FROM last_iter T-- "распаковка" матрицы , unpack AS ( SELECT * FROM json_to_recordset(result) unpack(x bigint, y bigint, cell bigint[]) )Тогда наша «пересборка» матрицы с фиксацией значения в ячейке будет выглядеть примерно так:
SELECT -- добавляем фиксируемую ячейку к json[] и превращаем в '[]'::json to_json(matrix_flt || vn) matrix FROM -- определяем фиксируемую ячейку ( SELECT * FROM unpack WHERE array_length(cell, 1) > 1 ORDER BY array_length(cell, 1), x, y LIMIT 1 ) fix -- собираем отфильтрованный json без этой ячейки , LATERAL ( SELECT array_agg(row_to_json(T)) FILTER(WHERE (x, y) <> (fix.x, fix.y)) matrix_flt FROM unpack T ) T0 -- организуем перебор вариантов значений , LATERAL unnest(cell) n -- формируем json-представление этой ячейки с конкретным значением , LATERAL ( SELECT row_to_json(T) vn FROM ( SELECT x , y , ARRAY[n] cell ) T ) T1Причем, наша рекурсия должна работать «в два хода» — сначала вычисляя результат по уже зафиксированным значениям, а потом генерирую подстановки для следующего шага, примерно как в статье «SQL HowTo: пишем while-цикл прямо в запросе, или «Элементарная трехходовка»». Для этого воспользуемся UNION ALL с противоположными условиями:
, rec_03 AS ( SELECT '{}'::json[] fixpath , json_agg(row_to_json(T)) matrix , NULL::json result , TRUE has_many , FALSE has_none FROM base T UNION ALL ( -- "материализуем" рекурсивную часть, чтобы обращаться к ней многократно WITH mv AS ( TABLE rec_03 ) ( -- вычисление результата "вычеркиваний" SELECT mv.fixpath , mv.matrix , T.result , T.has_many , T.has_none FROM mv , LATERAL ( WITH RECURSIVE unpack AS ( SELECT * FROM json_to_recordset(coalesce(result, matrix)) unpack(x bigint, y bigint, cell bigint[]) ) , rec_02 AS ( SELECT 1 lvl , * FROM unpack UNION ALL -- ... ) , last_iter AS ( SELECT x , y , cell FROM rec_02 WHERE lvl = (SELECT max(lvl) FROM rec_02) ) SELECT json_agg(row_to_json(T)) result , bool_or(array_length(cell, 1) > 1) has_many -- есть ячейки с несколькими значениями , bool_or(coalesce(cell, '{}') = '{}') has_none -- есть пустые ячейки FROM last_iter T ) T WHERE -- нечетный шаг mv.result IS NULL UNION ALL -- фиксация значений ячейки SELECT T.fixpath , T.matrix , NULL , mv.has_many , mv.has_none FROM mv , LATERAL ( WITH unpack AS ( SELECT * FROM json_to_recordset(coalesce(result, matrix)) unpack(x bigint, y bigint, cell bigint[]) ) -- ... пересборка матрицы ) T WHERE -- четный шаг mv.result IS NOT NULL AND -- пока нет пустых ячеек, но есть незафиксированные mv.has_many AND NOT mv.has_none ) ) )Обратите внимание, что unpack хоть и выглядит полностью одинаково, не может быть «вынесен за скобки», поскольку тогда будет применяться ко всем записям рекурсивного сегмента mv — а их там после unnest предыдущего шага заведомо несколько. А так использование LATERAL позволяет нам «распаковывать» каждую строку отдельно.
Рисуем итоговую картинку
-- находим запись с решением , unpack AS ( SELECT * FROM json_to_recordset(( SELECT result FROM rec_03 WHERE NOT has_many AND -- нет вариативности NOT has_none -- нет занулений LIMIT 1 )) unpack(x bigint, y bigint, cell bigint[]) ) -- собираем в матрицу SELECT string_agg( lpad(cell[1]::text, (SELECT length(m::text) FROM side)) , ' ' ORDER BY x ) line FROM unpack GROUP BY y ORDER BY y;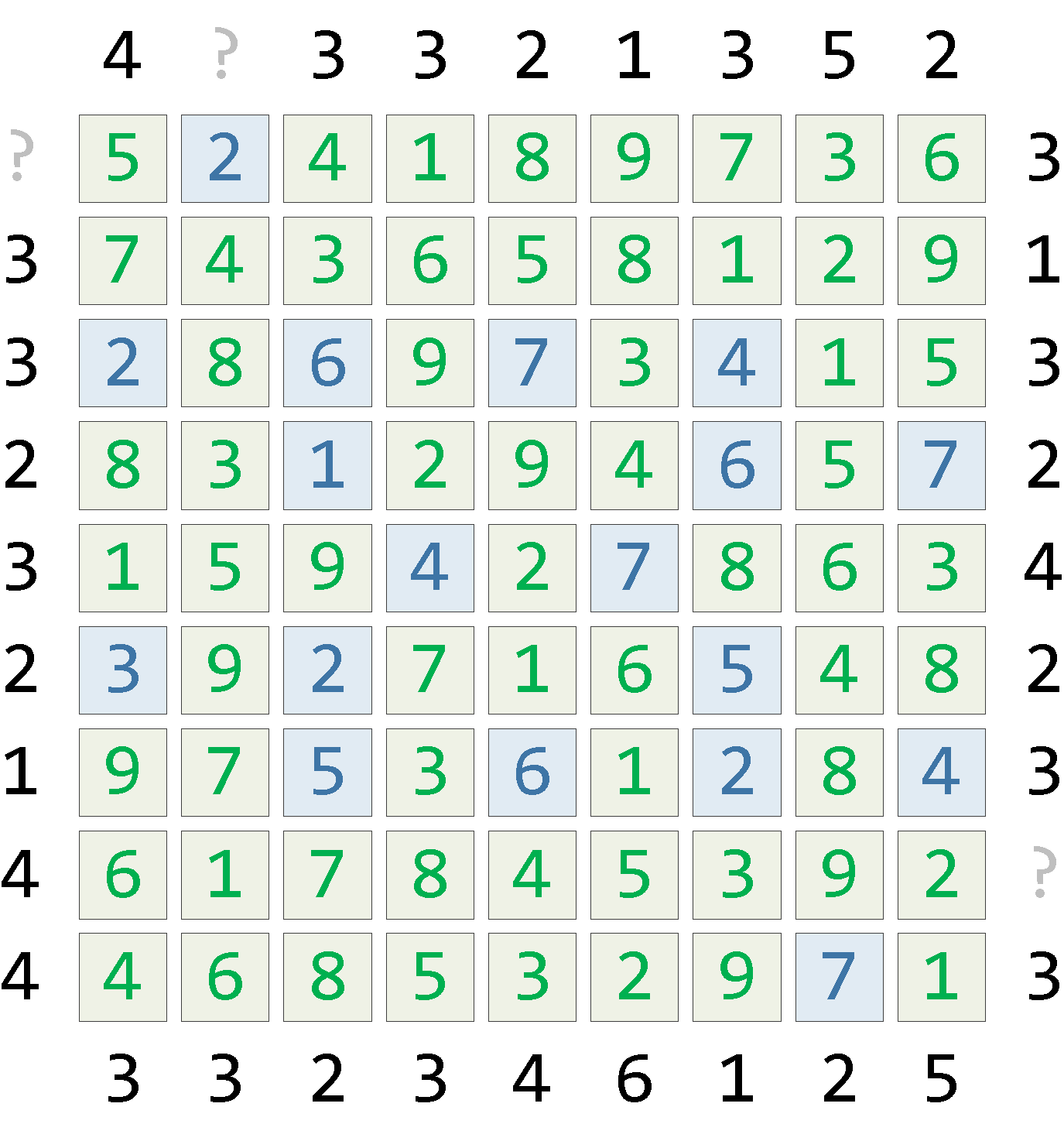
Общее время работы этого адового запроса — всего 250ms, ну, а полный его текст вы уже видели в начале статьи. (:
Надеюсь, что-то для себя новое или интересное в нем найдете и вы.
ссылка на оригинал статьи https://habr.com/ru/company/tensor/blog/552790/
Добавить комментарий