Главная задача этого поста – показать один мало применяемый в Python подход к работе функциями в рамках более общей функциональной парадигмы, в которой функциями можно манипулировать точно так же, как и любыми другими объектами: присваивать переменным, передавать в качестве аргументов в другие функции, возвращать из функций и включать в последовательности в качестве их элементов.
Функциональный стиль программирования очень близок к тому, как размышляет человек во время решения задачи. «Пусть дано x. В целях решения задачи с этими данными необходимо выполнить серию преобразований. Сначала применить к ним f и получить результирующие данные x'. Затем к новым данным применить f2 и получить новые результирующие данные x'' и т.д.
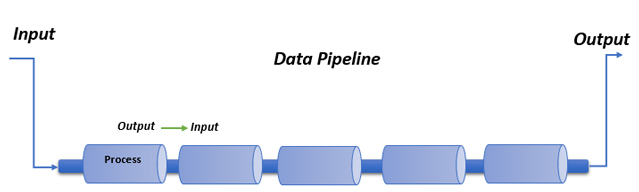
Как оказалось, такой образ мыслей отлично укладывается в то, что называется конвейером обработки данных. Конвейер обработки данных состоит из связанных между собой узлов, т.е. функций. Узел характеризуется набором входных и выходных каналов, по которым могут передаваться объекты. Узел ожидает появления определенного набора объектов на своем входном канале, после чего проводит вычисления и порождает объект(ы) на своем выходном канале, которые передаются в следующий узел в конвейере.
В функциональных языках конвейеры находят широкое применение, и для их имплементирования даже существуют специальные синтаксические конструкции. Вот как выглядит конвейер в языке F#:
2
|> ( fun x -> x + 5)
|> ( fun x -> x * x)
|> ( fun x -> x.ToString() )
Здесь входные данные, в данном случае число 2, последовательно обрабатываются серией лямбда-функций. Аналогичный конвейер можно имплементировать на языке Python, но для этого нужно написать специальную функцию, и, разумеется, это будет функция более высокого порядка:
# Конвейер обработки данных
def pipe(data, *fseq):
for fn in fseq:
data = fn(data)
return data
Приведенный ниже пример демонстрирует работу конвейера:
pipe(2,
lambda x: x + 5,
lambda x: x * x,
lambda x: str(x))
Число 2 проходит серию преобразований, и в результате будет получено строковое значение '49'. По сравнению с функцией reduce, в которой переданная в качестве аргумента одна единственная редуцирующая функция по очереди применяется к последовательности данных, в функции pipe наоборот последовательность функций применяется к обновляемым данным.
Функция pipe получает два аргумента: входные данные data и последовательность функций fseq. Во время первой итерации цикла for данные передаются в первую функцию из последовательности. Эта функция обрабатывает данные и возвращает результат, замещая переменную data новыми данными. Затем эти новые данные отправляются во вторую функцию и т.д. до тех пор, пока не будут выполнены все функции последовательности. По завершению своей работы функция pipe возвращает итоговые данные. Это и есть конвейер обработки данных.
Примечание. В приведенном выше примере функции pipe использован оператор упаковки *. В зависимости от контекста оператор * служит для упаковки получаемых нескольких аргументов в одну параметрическую переменную либо распаковки списка передаваемых в функцию аргументов.
Когда он используется в параметре функции, как в приведенном выше примере, он служит для упаковки всех аргументов в одну параметрическую переменную. Например,
def my_sum(*args): # Упаковка в список
return sum(args)
my_sum(1, 2, 3, 4, 5)
Когда он используется при вызове функции он служит для разложения передаваемого списка на отдельные аргументы. Например,
def fun(a, b, c, d):
print(a, b, c, d)
my_list = [1, 2, 3, 4]
fun(*my_list) # Разложение на четыре аргумента
В следующих ниже рубриках будут рассмотрены примеры применения конвейера обработки данных на основе функциональной парадигмы программирования.
Функциональная имплементация вычисления факториала числа
В приведенном ниже примере показана нерекурсивная версия алгоритма вычисления факториала (factorial) и его рекурсивной версия на основе более эффективной хвостовой рекурсии (factorial_rec). Детали имплементации обеих функций в данном случае не важны. Они приводятся в качестве примеров, на которых будет продемонстрирована работа конвейера обработки данных. Результат выполнения программы показан ниже.
1 # Эта программа демонстрирует
2 # функциональную версию функции factorial из главы 12
3
4 def main():
5 # Конвейер (ядро c нерекурсивным алгоритмом факториала)
6 pipe(int(input('Введите неотрицательное целое число: ')),
7 lambda n: (n, reduce(lambda x, y: x * y, range(1, n + 1))),
8 lambda tup:
9 print(f'Факториал числа {tup[0]} равняется {tup[1]}'))
# Вызвать главную функцию
main()
Вывод программы:
Введите неотрицательное целое число: 4 (Enter)
Факториал числа 4 равняется 24
В строке 8 лямбда-функция в последнем узле конвейера получает кортеж, состоящий из введенного пользователем числа и полученного результата.
В приведенную ниже расширенную версию программы вычисления факториала добавлена валидация входных данных, и алгоритмы выделены в отдельные функции. Чуть позже будет дано пояснение.
1 # Эта программа демонстрирует
2 # функциональную версию функции factorial из главы 12
3
4 def get_int(msg=''):
5 return int(input(msg))
6
7 def main():
8 # Алгоритм 1. Рекурсивная версия с хвостовой рекурсией
9 def factorial_rec(n):
10 fn = lambda n, acc=1: acc if n == 0 else fn(n - 1, acc * n)
11 return n, fn(n)
12
13 # Алгоритм 2. Нерекурсивная версия
14 def factorial(n):
15 return n, reduce(lambda x, y: x * y, range(1, n + 1))
16
17 # Ввод данных
18 def indata():
19 def validate(n): # Валидация входных данных
20 if not isinstance(n, int):
21 raise TypeError("Число должно быть целым.")
22 if not n >= 0:
23 raise ValueError("Число должно быть >= 0.")
24 return n
25 msg = 'Введите неотрицательное целое число: '
26 return pipe(get_int(msg), validate)
27
28 # Вывод данных
29 def outdata():
30 def fn(data):
31 n, fact = data
32 print(f'Факториал числа {n} равняется {fact}')
33 return fn
34
35 # Конвейер (функциональное ядро)
36 pipe(indata(), # вход: - выход: int
37 factorial, # вход: int выход: кортеж
38 outdata()) # вход: кортеж выход: -
39
40 # Вызвать главную функцию
41 main()
Вывод программы:
Введите неотрицательное целое число: 4 (Enter)
Факториал числа 4 равняется 24
Функциональным ядром программы являются строки 36-38:
pipe(indata(),
factorial,
outdata())
Они представлены конвейером из трех узлов, т.е. функциями indata, factorial и outdata. Функция indata занимается получением данных от пользователя, которые затем передаются по конвейеру дальше. Функция factorial является собственно обрабатывающим алгоритмом, в данном случае нерекурсивной функцией вычисления факториала, которая получает данные, их обрабатывает и передает по конвейеру дальше. И функция outdata получает данные и показывает их пользователю. Обратите внимание, что функция indata имеет свой собственный конвейер, который состоит из получения данных от пользователя и их валидации.
Следует отметить два важных момента. Во-первых, передаваемые от узла к узлу данные должны соответствовать какому-то определенному протоколу. Во-вторых, количество узлов может быть любым.
Такая организация программного кода:
-
Позволяет менять узлы конвейера на другие с целью тестирования различных и более эффективных имплементаций алгоритмов. Например, вместо нерекурсивной функции factorial, можно поместить рекурсивную функцию factorial_rec.
pipe(indata(), factorial_rec, outdata())
-
Облегчает проведение отладки программы, позволяя на каждом стыке вставлять отладочный код с целью проверки промежуточных результатов и тестирования производительности отдельных узлов.
Например, рассмотрим вторую возможность – отладку. В этом случае можно написать вспомогательную функцию check:
def check(data):
print(data)
return data
И затем ее вставить в конвейер, чтобы проверить результаты работы отдельных узлов конвейера:
pipe(indata(), check, factorial, check, outdata())
Если выполнить программу в таком варианте, то будут получены следующие результаты:
Вывод программы:
Введите неотрицательное целое число: 4 (Enter)
4
(4, 24)
Факториал числа 4 равняется 24
Как видно из результатов, на вход в функцию factorial поступает введенное пользователем значение 4, а на выходе из нее возвращается кортеж с исходным числом и полученным результатом (4, 24). Этот результат показывает, что программа работает, как и ожидалось. Как вариант, вместо проверочной функции можно написать функцию-таймер, которая могла бы хронометрировать отдельные узлы конвейера.
Приведем еще пару примеров с аналогичной организацией программного кода на основе функционального ядра в виде конвейера.
Функциональная имплементация вычисления последовательности Фибоначчи
# Эта программа демонстрирует
# функциональную версию функции fibonacci из главы 12
def main():
# Алгоритм
def fibonacci(n, x=0, y=1):
# Функция fib возвращает n-ое число последовательности.
fib = lambda n, x=0, y=1: x if n <= 0 else fib(n - 1, y, x + y)
# Функция reduce собирает результаты в список acc
acc = []
reduce(lambda _, y: acc.append(fib(y)), range(n + 1))
return n, acc
# Валидация входных данных
def validate(n):
if not isinstance(n, int):
raise TypeError("Число должно быть целым.")
if not n >= 0:
raise ValueError("Число должно быть ноль положительным.")
if n > 10:
raise ValueError("Число должно быть не больше 10.")
return n
# Ввод данных
def indata():
msg = 'Введите неотрицательное целое число не больше 10: '
return pipe(get_int(msg), validate)
# Вывод данных
def outdata():
def fn(data):
n, seq = data
msg = f'Первые {n} чисел последовательности Фибоначчи:'
print(msg)
[print(el) for el in seq]
return fn
# Конвейер (функциональное ядро)
pipe(indata(), fibonacci, outdata())
# Вызвать главную функцию.
main()
Вывод программы
Введите неотрицательное целое число не больше 10: 10 (Enter)
Первые 10 чисел последовательности Фибоначчи:
1
1
2
3
5
8
13
21
34
55
Функциональная имплементация суммирования диапазона значений последовательности
# Эта программа демонстрирует
# функциональную версию функции range_sum из главы 12
def main():
# Алгоритм
def range_sum(data):
seq, params = data
fn = lambda start, end: 0 if start > end \
else seq[start] + fn(start + 1, end)
return fn(*params)
# Ввод данных
def indata():
seq = [1, 2, 3, 4, 5, 6, 7, 8, 9]
params = (2,5) # params - это параметры start, end
return seq, params
# Вывод данных
def outdata():
def f(data):
msg = 'Сумма значений со 2 по 5 позиции равняется '
print(msg, format(data), sep='')
return f
# Конвейер (функциональное ядро)
pipe(indata(), range_sum, outdata())
# Вызвать главную функцию.
main()
Вывод программы
Сумма значений со 2 по 5 позиции равняется 18
Приведенный в настоящей главе материал имеет ознакомительный характер и предназначен для того, чтобы продемонстрировать возможности функционального парадигмы программирования на Python с целью дальнейших самостоятельных исследований и побудить программистов дать функциональному стилю шанс. Исходный код поста находится в моем репо на Github.
ссылка на оригинал статьи https://habr.com/ru/post/555370/
Добавить комментарий