Майнкрафт для геологов: 3D-рендеринг миллиарда ячеек на встроенной видеокарте (часть 2)

В первой части статьи мы реализовали простой (и не очень эффективный) рендерер сетки ГУТ, и пообещали, что оптимизируем рендерер настолько, что он сможет отобразить заявленный в заголовке миллиард ячеек.

Для этого нам придётся значительно сократить объём потребляемой видеопамяти — в текущем виде даже на игровых видеокартах (если бы их можно было купить в наше время!) памяти может не хватить, не говоря уж о видеокартах в офисных компьютерах.

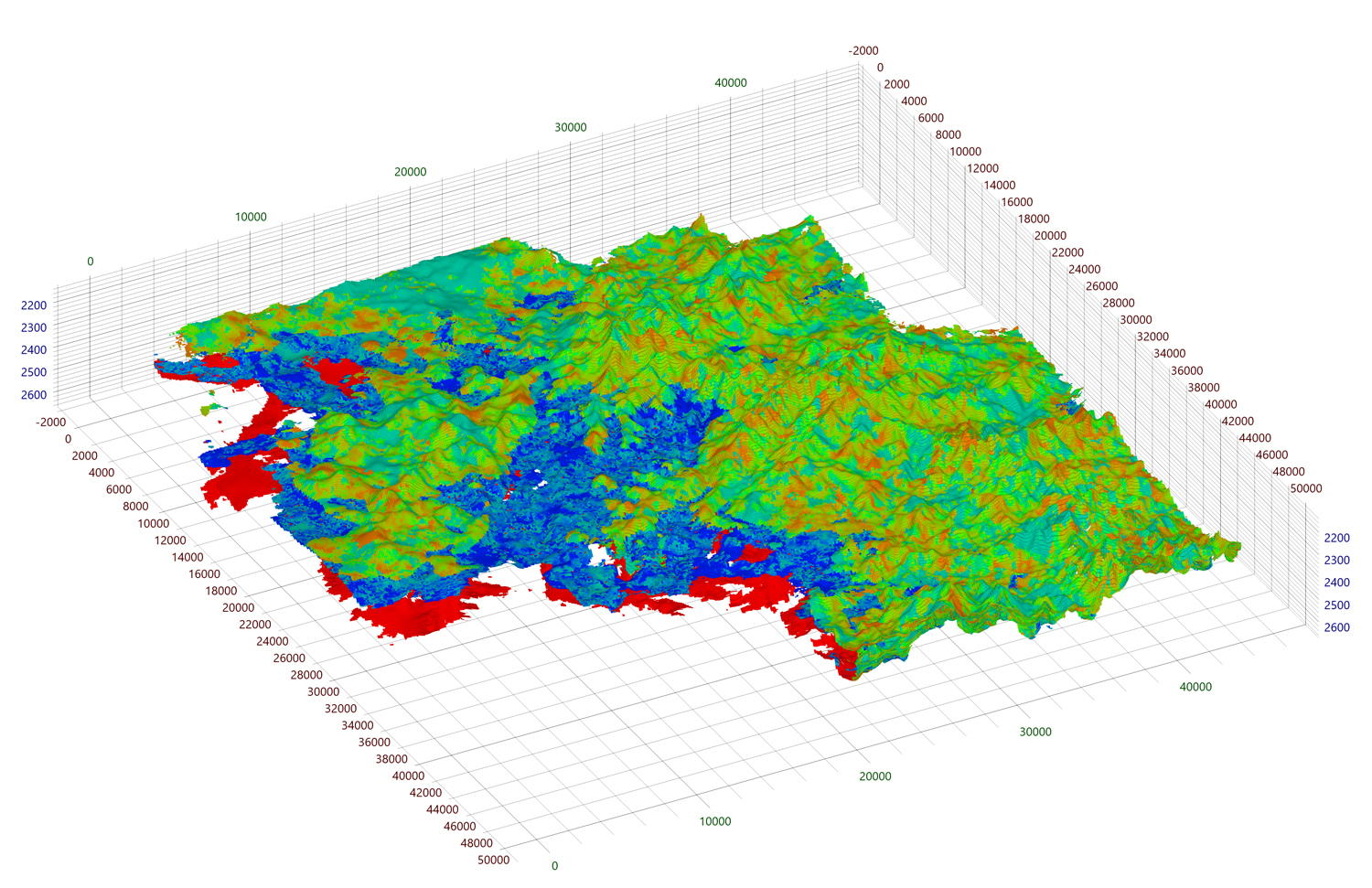
Начнём с того, что проанализируем, сколько памяти требует наш рендерер сейчас. Каждая грань ячейки задана на четырёх вершинах, каждая вершина содержит пять атрибутов общим объёмом в 48 байт. Предположим, что на вход подаётся полностью состыкованная сетка размером 1000³. В этом случае будет сгенерировано 4*6*1000² вершин для внешних граней сетки, общим объёмом 1098,6 Мб. Не будем забывать и про индексы, коих будет сгенерировано 6*6*1000² шт. размером 137,3 Мб.

В реальности, сетки ГУТ часто не полностью состыкованы и обычно имеют маску активности ячеек, из-за чего не отсечённых граней может быть гораздо больше.

Представим пару соседних ячеек, одна из которых активна, а другая – нет. Алгоритм отсечения невидимых граней (см. первую часть статьи) скажет, что для активной ячейки нужно рисовать грань со стороны неактивной ячейки. Таким образом, чем больше в сетке неактивных ячеек, тем больше граней будет создано. 

Чтобы проиллюстрировать этот случай, сгенерируем тестовую сетку сравнительно небольшого размера — всего 200³ ячеек. Подвох в том, что ровно половину из ячеек случайным образом сделали неактивными — это худший случай для нашего алгоритма отсечения невидимых граней.

Может показаться, что этот пример является надуманным, но с точки зрения отсечения невидимых граней нет разницы, оставлена ли грань из-за нестыкованности или из-за неактивности соседней ячейки.

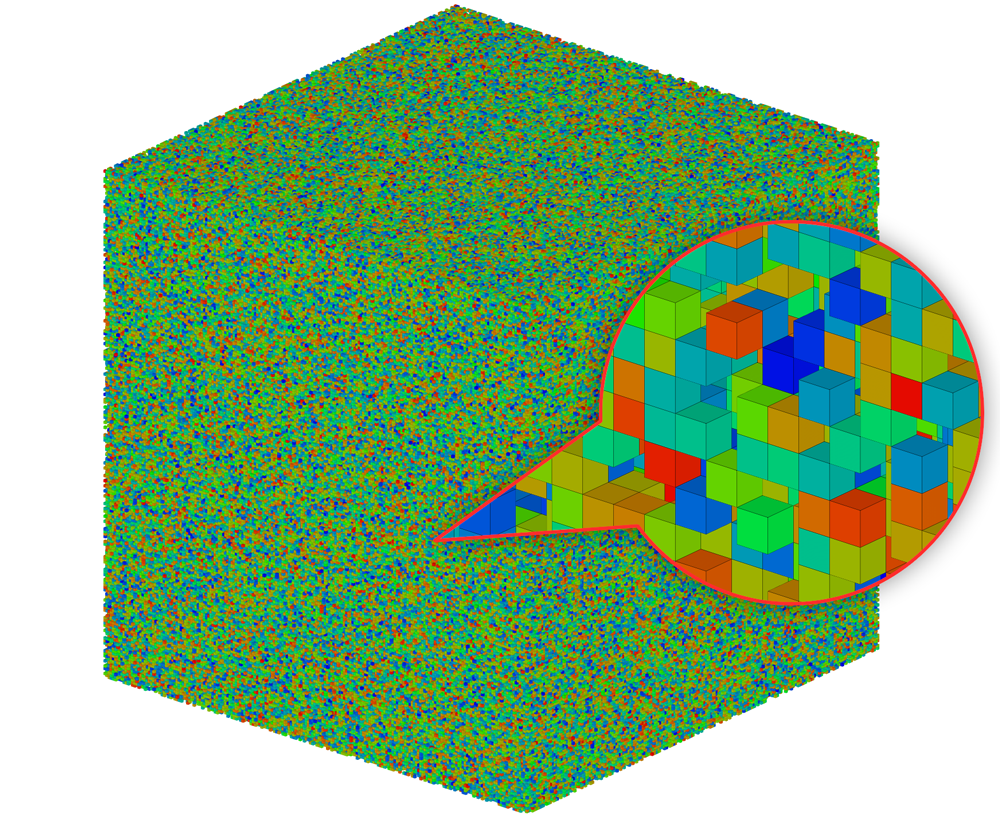
Для этой сравнительно небольшой сетки объём занимаемой памяти под вершины и индексы составил 2484,3 Мб — в два раза больше, чем для миллиарда состыкованных ячеек!

Для удобства читателя приведём исходный код рендерера из первой части статьи:

// corner_point_grid.h  template<typename T> struct span3d {      T* const data;     const uint32_t ni;     const uint32_t nj;     const uint32_t nk;      span3d(T* _data, uint32_t _ni, uint32_t _nj, uint32_t _nk)         : data(_data), ni(_ni), nj(_nj), nk(_nk) { }      T at(size_t x, size_t y, size_t z) const {         return data[x * nj * nk + y * nk + z];     }      T& at(size_t x, size_t y, size_t z) {         return data[x * nj * nk + y * nk + z];     } };   struct Palette {     float min_value;     float max_value;     GLuint texture; };   struct CornerPointGrid {     CornerPointGrid(uint32_t ni, uint32_t nj, uint32_t nk,                     const float* coord, const float *zcorn, const float* property, const uint8_t* mask);     ~CornerPointGrid();      void render(GLuint shader,                 const Palette& palette,                 const mat4& proj, const mat4 & view,                 const mat4& model,                 vec3 light_direct,                 bool primitive_picking);  private:      // входные данные     span3d<const float>   _coord;     span3d<const float>   _zcorn;     span3d<const float>   _property;     span3d<const uint8_t> _mask;      // маска состыкованности граней     std::vector<uint8_t>  _joined_mask_data;     span3d<uint8_t>  _joined_mask; // ссылается на массив _joined_mask_data;      // объекты OpenGL     GLuint _position_vbo;     GLuint _normal_vbo;     GLuint _cell_index_vbo;     GLuint _texcoord_vbo;     GLuint _property_vbo;      GLuint _indexbuffer;     GLuint _vao;      // число треугольников для рендеринга     size_t _triangle_count;      // расчет вершин и индексов     void _gen_vertices_and_indices(size_t quad_count);      // создание буферов OpenGL     void _create_vertex_index_buffers();      // назначение буферов в VAO     void _setup_vao(); };   // corner_point_grid.cpp  // Для каждой ячейки нужно получить координаты восьми её вершин. //         6-------7 //        /|     / | //       4------5  |    z y //       | 2----|--3    |/ //       |/     | /     0-x //       0------1 // Эти массивы определяют отступы для получения каждой из 8-ми вершин // ячейки по осям x, y, z, если рассматривать только одну ячейку. static const std::array<uint32_t, 8> cell_vertices_offset_x = {     0, 1, 0, 1, 0, 1, 0, 1 }; static const std::array<uint32_t, 8> cell_vertices_offset_y = {     0, 0, 1, 1, 0, 0, 1, 1 }; static const std::array<uint32_t, 8> cell_vertices_offset_z = {     0, 0, 0, 0, 1, 1, 1, 1 };  // Индексы вершин, формирующие грани ячейки. //         6-------7 //        /|     / | //       4------5  |    z y //       | 2----|--3    |/ //       |/     | /     0-x //       0------1 static const std::array<std::array<uint32_t, 4>, 6> cell_quads = {     std::array<uint32_t, 4>{0, 1, 5, 4},   // 1-ая грань     std::array<uint32_t, 4>{1, 3, 7, 5},   // 2-ая грань     std::array<uint32_t, 4>{3, 2, 6, 7},   // ...     std::array<uint32_t, 4>{2, 0, 4, 6},     std::array<uint32_t, 4>{3, 1, 0, 2},     std::array<uint32_t, 4>{4, 5, 7, 6}, };  // Для каждой грани индексы соседней ячейки со стороны этой грани static const std::array<std::array<int, 3>, 6> cell_quads_neighbors = {     // прибавим их к координатам (i,j,k) ячейки - получим координаты соседней ячейки     std::array<int, 3>{ 0, -1,  0},     std::array<int, 3>{ 1,  0,  0},     std::array<int, 3>{ 0,  1,  0},     std::array<int, 3>{-1,  0,  0},     std::array<int, 3>{ 0,  0, -1},     std::array<int, 3>{ 0,  0,  1}, };  // битовые маски, с помощью которой можно узнать стыкована ли ячейка с одной из соседних // (просмотрев соответствующий маске бит в массиве joined_mask) enum JoinedMaskBits : uint8_t {     I_PREV = 1 << 0, I_NEXT = 1 << 1,     J_PREV = 1 << 2, J_NEXT = 1 << 3,     K_PREV = 1 << 4, K_NEXT = 1 << 5 };  // Для каждой грани бит, показывающий стыкованность с соседней ячейкой static const std::array<JoinedMaskBits, 6> cell_quads_joined_mask_bits = {     // то есть ячейка является соседней по оси x, y или z     JoinedMaskBits::J_PREV,     JoinedMaskBits::I_NEXT,     JoinedMaskBits::J_NEXT,     JoinedMaskBits::I_PREV,     JoinedMaskBits::K_PREV,     JoinedMaskBits::K_NEXT, };  // Для того, чтобы рисовать сетку на границах ячеек, // надо знать насколько близко расположен пиксель к границе. // Тут перечислены текстурные координаты для каждой вершины грани, // которые позволят получить расстояние до границы // (если один из компонентов равен нулю, то это и есть граница). static const std::array<vec2, 4> quad_vertices_texcoords = {     vec2(1, 0),     vec2(0, 0),     vec2(0, 1),     vec2(0, 0), };  // Как для грани сформировать два треугольника static const std::array<uint32_t, 6> quad_to_triangles = {     0, 1, 2, 0, 2, 3 };   static vec3 calc_normal(vec3 v1, vec3 v2){     // посчитаем нормаль к кваду     vec3 normal = cross(v1, v2);      // приведем нормаль к единичной длине     if (length2(normal) < 1e-8f){         normal = vec3(0, 0, 1);     } else {         normal = normalize(normal);     }      return normal; }   static void calc_joined_mask(span3d<const float> zcorn, span3d<uint8_t> joined_mask) {     // с какой точностью сравниваем совпадание граней, ~10 см вполне достаточно.     const float eps = 0.1f;      // для каждой ячейки результирующей маски     for(uint32_t i = 0; i < joined_mask.ni; ++i) {         for(uint32_t j = 0; j < joined_mask.nj; ++j) {             for(uint32_t k = 0; k < joined_mask.nk; ++k) {                 // индексы этой ячейки в zcorn                 uint32_t iz = i * 2, jz = j * 2, kz = k * 2;                  // проверяем, совпадают ли граничные вершины ячеек (i,j,k) и (i+1,j,k) по оси X                 if (i + 1 < joined_mask.ni) {                     float d = 0.0f;                     d += std::abs(zcorn.at(iz+1, jz,   kz  ) - zcorn.at(iz+2, jz,   kz  ));                     d += std::abs(zcorn.at(iz+1, jz+1, kz  ) - zcorn.at(iz+2, jz+1, kz  ));                     d += std::abs(zcorn.at(iz+1, jz,   kz+1) - zcorn.at(iz+2, jz,   kz+1));                     d += std::abs(zcorn.at(iz+1, jz+1, kz+1) - zcorn.at(iz+2, jz+1, kz+1));                      if (d < eps) {                         // совпадают - отметим стыкованность, установив биты I_NEXT и I_PREV                         joined_mask.at(i,   j, k) |= I_NEXT;                         joined_mask.at(i+1, j, k) |= I_PREV;                     }                 }                  // проверяем, совпадают ли граничные вершины ячеек (i,j,k) и (i,j+1,k) по оси Y                 if (j + 1 < joined_mask.nj) {                     float d = 0.0f;                     d += std::abs(zcorn.at(iz,   jz+1, kz  ) - zcorn.at(iz,   jz+2, kz  ));                     d += std::abs(zcorn.at(iz+1, jz+1, kz  ) - zcorn.at(iz+1, jz+2, kz  ));                     d += std::abs(zcorn.at(iz,   jz+1, kz+1) - zcorn.at(iz,   jz+2, kz+1));                     d += std::abs(zcorn.at(iz+1, jz+1, kz+1) - zcorn.at(iz+1, jz+2, kz+1));                      if (d < eps) {                         // совпадают - отметим стыкованность, установив биты J_NEXT и J_PREV                         joined_mask.at(i, j,   k) |= J_NEXT;                         joined_mask.at(i, j+1, k) |= J_PREV;                     }                 }                  // проверяем, совпадают ли граничные вершины ячеек (i,j,k) и (i,j,k+1) по оси Z                 if (k + 1 < joined_mask.nk) {                     float d = 0.0f;                     d += std::abs(zcorn.at(iz,   jz,   kz+1) - zcorn.at(iz,   jz,   kz+2));                     d += std::abs(zcorn.at(iz+1, jz,   kz+1) - zcorn.at(iz+1, jz,   kz+2));                     d += std::abs(zcorn.at(iz,   jz+1, kz+1) - zcorn.at(iz,   jz+1, kz+2));                     d += std::abs(zcorn.at(iz+1, jz+1, kz+1) - zcorn.at(iz+1, jz+1, kz+2));                      if (d < eps) {                         // совпадают - отметим стыкованность, установив биты K_NEXT и K_PREV                         joined_mask.at(i, j, k)   |= K_NEXT;                         joined_mask.at(i, j, k+1) |= K_PREV;                     }                 }             } // for k         } // for j     } // for i }  static bool check_if_quad_culled(const span3d<const uint8_t>& mask,                                  const span3d<uint8_t>& joined_mask,                                  uint32_t i, uint32_t j, uint32_t k, uint32_t qi) {      // грани создавать нужно только для тех сторон, которые не состыкованы с соседними     if (!(joined_mask.at(i, j, k) & cell_quads_joined_mask_bits[qi]))         return false;      // или если соседняя ячейка не отображается     // (выход за границы не проверяем, т.к. по границе _joined_mask == 0)     if (!mask.at(i + cell_quads_neighbors[qi][0],                  j + cell_quads_neighbors[qi][1],                  k + cell_quads_neighbors[qi][2]))         return false;      // обе проверки не прошли, значит грань можно отсечь     return true; }  static size_t calc_number_of_quads(const span3d<const uint8_t>& mask,                                    const span3d<uint8_t> joined_mask) {     size_t num_of_quads = 0;      for (uint32_t i = 0; i < mask.ni; ++i)         for (uint32_t j = 0; j < mask.nj; ++j)             for (uint32_t k = 0; k < mask.nk; ++k)                  // если ячейка активна                 if (mask.at(i, j, k)){                      // для каждого возможного полигона                     for (uint32_t qi = 0; qi < 6; ++qi){                          // определим, нужно ли его создавать                         if (!check_if_quad_culled(mask, joined_mask, i, j, k, qi))                             // и если нужно, то увеличим счетчик                             num_of_quads++;                     }                 }      return num_of_quads; }   // Получаем все 8 вершин, соответствующих ячейке (i, j, k). //     6-------7 //    /|     / | //   4------5  | //   | 2----|--3 //   |/     | / //   0------1 static void get_cell_vertices(const span3d<const float>& coord,                               const span3d<const float>& zcorn,                               uint32_t i, uint32_t j, uint32_t k,                               std::array<vec3, 8>& vertices) {      // для каждой вершины     for (int vi = 0; vi < 8; ++vi) {          // получим индексы пиллара по индексам ячейки         uint32_t pillar_index_i = i + cell_vertices_offset_x[vi];         uint32_t pillar_index_j = j + cell_vertices_offset_y[vi];          // p1 - первая точка пиллара         float p1_x = coord.at(pillar_index_i, pillar_index_j, 0);         float p1_y = coord.at(pillar_index_i, pillar_index_j, 1);         float p1_z = coord.at(pillar_index_i, pillar_index_j, 2);         // p2 - вторая точка пиллара         float p2_x = coord.at(pillar_index_i, pillar_index_j, 3);         float p2_y = coord.at(pillar_index_i, pillar_index_j, 4);         float p2_z = coord.at(pillar_index_i, pillar_index_j, 5);          // значение Z для ячейки у нас есть, а X и Y нет,         // зато известно, что (x,y,z) лежит на линии пиллара p1-p2         float z = zcorn.at(2 * i + cell_vertices_offset_x[vi],                            2 * j + cell_vertices_offset_y[vi],                            2 * k + cell_vertices_offset_z[vi]);          float t = (z - p1_z) / (p2_z - p1_z);         float x = p1_x + (p2_x - p1_x) * t;         float y = p1_y + (p2_y - p1_y) * t;         vertices[vi].x = x;         vertices[vi].y = y;         vertices[vi].z = z;     } }  void CornerPointGrid::_gen_vertices_and_indices(size_t quad_count) {      const size_t vertex_count = quad_count * 4;      std::vector<float> a_position, a_index, a_property, a_normal, a_texcoord;     // для каждой вершины 3 координаты (x, y и z)     a_position.reserve(3 * vertex_count);     // + три индекса     a_index.reserve(3 * vertex_count);     // + значение свойства ячейки     a_property.reserve(vertex_count);     // + три компоненты нормали     a_normal.reserve(3 * vertex_count);     // + две текстурные координаты (расстояние от вершин до противолежащих сторон)     a_texcoord.reserve(2 * vertex_count);       // буфер, куда записываются вершины ячейки     std::array<vec3, 8> cell_vertices;      // для каждой рассматриваемой ячейки     for (uint32_t i = 0; i < _property.ni; ++i) {         for (uint32_t j = 0; j < _property.nj; ++j) {             for (uint32_t k = 0; k < _property.nk; ++k) {                  // если ячейка может отрисовываться (они фильтруются по маске)                 if (_mask.at(i, j, k)){                      // рассчитаем 8 вершин, соответствующих ячейке                     get_cell_vertices(_coord, _zcorn, i, j, k, cell_vertices);                      // из вершин формируем грани                     for (int qi = 0; qi < 6; ++qi) {                         // определим, нужно ли создавать грань                         if (!check_if_quad_culled(_mask, _joined_mask, i, j, k, qi)){                              // 4 индекса вершин грани                             const std::array<uint32_t, 4>& quad = cell_quads[qi];                              // посчитаем нормаль грани                             vec3 normal = calc_normal(                                         cell_vertices[quad[0]] - cell_vertices[quad[1]],                                         cell_vertices[quad[2]] - cell_vertices[quad[1]]);                              // для каждой вершины в полигоне                             for (int vii = 0; vii < 4; ++vii){                                  // координаты очередной вершины                                 const vec3& v = cell_vertices[quad[vii]];                                  // записываем атрибуты вершины                                 a_position.insert(a_position.end(), {v.x, v.y, v.z});                                 a_index.insert(a_index.end(), {(float)i, (float)j, (float)k});                                 a_property.push_back(_property.at(i, j, k));                                 a_normal.insert(a_normal.end(), {normal.x, normal.y, normal.z});                                 vec2 texcoords = quad_vertices_texcoords[vii];                                 a_texcoord.insert(a_texcoord.end(), {texcoords.x, texcoords.y});                             }                         }                     }                 }             }         }     }      assert(a_position.size() == vertex_count * 3);      // загружаем атрибуты в VBO     glNamedBufferStorage(_position_vbo,    a_position.size() * sizeof (float),       a_position.data(), gl::GL_NONE_BIT);     glNamedBufferStorage(_normal_vbo,      a_normal.size() * sizeof (float),     a_normal.data(), gl::GL_NONE_BIT);     glNamedBufferStorage(_cell_index_vbo, a_index.size() * sizeof (float),     a_index.data(), gl::GL_NONE_BIT);     glNamedBufferStorage(_texcoord_vbo,    a_texcoord.size() * sizeof (float),   a_texcoord.data(), gl::GL_NONE_BIT);     glNamedBufferStorage(_property_vbo,   a_property.size() * sizeof (float),    a_property.data(), gl::GL_NONE_BIT);       // создадим массив индексов - на каждую грань два треугольника     size_t indices_count = quad_count * 6;     std::vector<uint32_t> indices;     indices.reserve(indices_count);      for (size_t i = 0; i < quad_count; ++i)         for (uint32_t j = 0; j < 6; ++j)             // индекс очередной вершины при составлении треугольников             indices.push_back(static_cast<uint32_t>(i * 4 + quad_to_triangles[j]));      glNamedBufferStorage(_indexbuffer, indices.size() * sizeof (uint32_t), indices.data(), gl::GL_NONE_BIT);      // запомним число индексов, нужно для glDrawElements     _triangle_count = indices.size(); }  void CornerPointGrid::_create_vertex_index_buffers() {     // вершинные буферы     glCreateBuffers(1, &_position_vbo);     glCreateBuffers(1, &_normal_vbo);     glCreateBuffers(1, &_cell_index_vbo);     glCreateBuffers(1, &_texcoord_vbo);     glCreateBuffers(1, &_property_vbo);      // индексный буфер     glCreateBuffers(1, &_indexbuffer); }  void CornerPointGrid::_setup_vao() {     // создаем VAO     glCreateVertexArrays(1, &_vao);     // назначаем индексный буфер в VAO     glVertexArrayElementBuffer(_vao, _indexbuffer);      // назначаем все атрибуты в VAO     // position     glVertexArrayVertexBuffer(_vao, 0, _position_vbo, 0, sizeof (float) * 3);     glVertexArrayAttribBinding(_vao, 0, 0);     glVertexArrayAttribFormat(_vao, 0, 3, GL_FLOAT, GL_FALSE, 0);     glEnableVertexArrayAttrib(_vao, 0);      // normal     glVertexArrayVertexBuffer(_vao, 1, _normal_vbo, 0, sizeof (float) * 3);     glVertexArrayAttribBinding(_vao, 1, 1);     glVertexArrayAttribFormat(_vao, 1, 3, GL_FLOAT, GL_FALSE, 0);     glEnableVertexArrayAttrib(_vao, 1);      // cell index     glVertexArrayVertexBuffer(_vao, 2, _cell_index_vbo, 0, sizeof (float) * 3);     glVertexArrayAttribBinding(_vao, 2, 2);     glVertexArrayAttribFormat(_vao, 2, 3, GL_FLOAT, GL_FALSE, 0);     glEnableVertexArrayAttrib(_vao, 2);      // texcoord     glVertexArrayVertexBuffer(_vao, 3, _texcoord_vbo, 0, sizeof (float) * 2);     glVertexArrayAttribBinding(_vao, 3, 3);     glVertexArrayAttribFormat(_vao, 3, 2, GL_FLOAT, GL_FALSE, 0);     glEnableVertexArrayAttrib(_vao, 3);      // property     glVertexArrayVertexBuffer(_vao, 4, _property_vbo, 0, sizeof (float));     glVertexArrayAttribBinding(_vao, 4, 4);     glVertexArrayAttribFormat(_vao, 4, 1, GL_FLOAT, GL_FALSE, 0);     glEnableVertexArrayAttrib(_vao, 4); }  CornerPointGrid::CornerPointGrid(uint32_t ni, uint32_t nj, uint32_t nk,                                  const float* coord, const float* zcorn, const float* property, const uint8_t* mask) :     _coord(coord,       ni+1, nj+1, 6),     _zcorn(zcorn,       ni*2, nj*2, nk*2),     _property(property, ni, nj, nk),     _mask(mask,         ni, nj, nk),     _joined_mask_data(ni*nj*nk, 0),     _joined_mask(_joined_mask_data.data(), ni, nj, nk) {      // посчитаем маску стыкованности ячеек     calc_joined_mask(_zcorn, _joined_mask);      // рассчитаем число видимых граней     size_t quad_count = calc_number_of_quads(_mask, _joined_mask);      // создаем вершинные и индексный буферы     _create_vertex_index_buffers();      // рассчитаем вершины и индексы и загрузим их в вершинные/индексные буферы     _gen_vertices_and_indices(quad_count);      // назначаем наши вершинные и индексный буфер в VAO     _setup_vao(); }  CornerPointGrid::~CornerPointGrid() {     glDeleteVertexArrays(1, &_vao);     glDeleteBuffers(1, &_position_vbo);     glDeleteBuffers(1, &_normal_vbo);     glDeleteBuffers(1, &_cell_index_vbo);     glDeleteBuffers(1, &_texcoord_vbo);     glDeleteBuffers(1, &_property_vbo);     glDeleteBuffers(1, &_indexbuffer); }  void CornerPointGrid::render(GLuint shader,                             const Palette& palette,                             const mat4& proj,                             const mat4& view,                             const mat4& model,                             vec3 light_direct,                             bool primitive_picking) {     // подразумеваем, что вызывающий код настроил фреймбуфер,     // включил тест и запись глубины, включил backface culling     glUseProgram(shader);      // матрица MVP     mat4 mvp = proj * view * model;     glProgramUniformMatrix4fv(shader, glGetUniformLocation(shader, "u_mvp"), 1, GL_FALSE, &mvp[0][0]);      // матрица поворота нормалей     mat3 normal_mat = transpose(inverse(mat3{model}));     glProgramUniformMatrix3fv(shader, glGetUniformLocation(shader, "u_normal_mat"), 1, GL_FALSE, &normal_mat[0][0]);      // направление света и режим пикинга     glProgramUniform3fv(shader, glGetUniformLocation(shader, "u_light_direct"), 1, &light_direct[0]);     glProgramUniform1i(shader, glGetUniformLocation(shader, "u_primitive_picking"), primitive_picking);      // палитра     glBindTextureUnit(0, palette.texture);     glProgramUniform2f(shader, glGetUniformLocation(shader, "u_value_range"), palette.min_value, palette.max_value);      // рисуем     glBindVertexArray(_vao);     glDrawElements(GL_TRIANGLES, _triangle_count, GL_UNSIGNED_INT, nullptr);      // сбрасываем все состояние на дефолтное     glBindVertexArray(0);     glBindTextureUnit(0, 0);     glUseProgram(0); }    // corner_point_grid.vert #version 440  // позиция layout(location=0) in vec3 a_pos; // нормаль layout(location=1) in vec3 a_normal; // индекс ячейки layout(location=2) in vec3 a_ind; // текстурные координаты layout(location=3) in vec2 a_texcoord; // значение в ячейке, по которому можно получить цвет layout(location=4) in float a_property;  // текстура с палитрой layout(binding=0) uniform sampler1D u_palette_tex;  // матрицы MVP-преобразования layout(location=0) uniform mat4 u_mvp; // матрица поворота нормалей layout(location=1) uniform mat3 u_normal_mat; // какому диапазону значений соответствует текстура layout(location=2) uniform vec2 u_value_range; // режим отрисовки layout(location=3) uniform bool u_primitive_picking; // вектор направления света layout(location=4) uniform vec3 u_light_direct;   layout(location=0) out INTERFACE {     // цвет вершины     vec4 color;     // текстурные координаты     vec2 texcoord; } vs_out;    void main() {      // проводим mvp-преобразования позиции     gl_Position = u_mvp * vec4(a_pos, 1);      // передаем текстурные координаты в фрагментный шейдер     vs_out.texcoord = a_texcoord;      // если делаем пикинг индексов ячеек, вместо цвета передаем во фрагментный шейдер индексы ячейки     if (u_primitive_picking) {         vs_out.color = vec4(a_ind.x, a_ind.y, a_ind.z, 1);         return;     }      // приводим значение свойства ячейки к диапазону палитры     float normalized_value = (a_property - u_value_range.x) / (u_value_range.y - u_value_range.x);     // получим цвет в текстуре палитры     vec4 cell_color = texture(u_palette_tex, normalized_value);      // рассчитываем повернутую нормаль     vec3 normal = normalize(u_normal_mat * a_normal);      // косинус угла между нормалью и направлением освещения     float NdotL = max(0, dot(normal, u_light_direct));     // закраска по фонгу     const float ka = 0.1, kd = 0.7;     vs_out.color = vec4((ka + NdotL * kd) * cell_color.rgb, cell_color.a);  }  // corner_point_grid.frag #version 440  // режим отрисовки layout(location=3) uniform bool u_primitive_picking;   layout(location = 0) in INTERFACE {     vec4 color;     vec2 texcoord; } fs_in;  layout(location=0) out vec4 FragColor;   // цвет фрагмента с учетом необходимости рисовать границы ячеек vec3 border_color(vec2 dist, vec3 color) {     // на сколько изменяется dist (1 - вершина, 0 - противоположная граница)     // при сдвиге на один пиксель в cторону границы     vec2 delta = fwidth(dist);     // высота тругольника, проведенная к рассматриваемой границе     vec2 len = 1.0 / delta;      // расстояние до границы меньше пикселя - только тогда надо рисовать границу,     vec2 edge_factor = smoothstep(0.2, 0.8, len * dist);      // смешиваем цвет с сеткой     return mix(color * 0.25, color, min(edge_factor.x, edge_factor.y)); }  void main() {     if (u_primitive_picking) {         FragColor = fs_in.color;         return;     }      // добавляем сетку     vec3 res_color =  border_color(fs_in.texcoord, fs_in.color.rgb);      FragColor = vec4(res_color, fs_in.color.a); }

Избавляемся от ненужных атрибутов

Посмотрим ещё раз на список атрибутов вершин:

1.                  координаты вершины (3*4 байт);

2.                  нормаль грани (3*4 байт);

3.                  индексы ячейки (3*4 байт);

4.                  текстурные координаты (2*4 байт);

5.                  значение свойства в ячейке (4 байта).

В первой части мы упоминали, что «красивость» стоит далеко не на первом месте в списке требований к рендереру. Поэтому обратим внимание на атрибут нормали граней. Нам совсем необязательно, чтобы нормаль была гладкой по всей грани — можно вычислять «плоскую» нормаль в шейдере, а от атрибута нормали избавиться, сэкономив 12 байт на каждую вершину.

Сначала удалим все упоминания нормалей из функции генерации вершин:

void CornerPointGrid::_gen_vertices_and_indices(size_t quad_count) {      const size_t vertex_count = quad_count * 4;      // УДАЛЕНО // std::vector<float> a_position, a_index, a_property, a_normal, a_texcoord;     std::vector<float> a_position, a_index, a_property, a_texcoord;     // для каждой вершины 3 координаты (x, y и z)     a_position.reserve(3 * vertex_count);     // + три индекса     a_index.reserve(3 * vertex_count);     // + значение свойства ячейки     a_property.reserve(vertex_count);     // УДАЛЕНО // + три компоненты нормали     // УДАЛЕНО // a_normal.reserve(3 * vertex_count);     // + две текстурные координаты (расстояние от вершин до противолежащих сторон)     a_texcoord.reserve(2 * vertex_count);      // …      // определим, нужно ли создавать грань     if (!check_if_quad_culled(_mask, _joined_mask, i, j, k, qi)){          // 4 индекса вершин грани         const std::array<uint32_t, 4>& quad = cell_quads[qi];          // посчитаем нормаль грани         // УДАЛЕНО // vec3 normal = calc_normal(         // УДАЛЕНО //             cell_vertices[quad[0]] - cell_vertices[quad[1]],         // УДАЛЕНО //             cell_vertices[quad[2]] - cell_vertices[quad[1]]);          // для каждой вершины в полигоне         for (int vii = 0; vii < 4; ++vii){              // координаты очередной вершины             const vec3& v = cell_vertices[quad[vii]];              // записываем атрибуты вершины             a_position.insert(a_position.end(), {v.x, v.y, v.z});             a_index.insert(a_index.end(), {(float)i, (float)j, (float)k});             a_property.push_back(_property.at(i, j, k));             // УДАЛЕНО // a_normal.insert(a_normal.end(), {normal.x, normal.y, normal.z});             vec2 texcoords = quad_vertices_texcoords[vii];             a_texcoord.insert(a_texcoord.end(), {texcoords.x, texcoords.y});         }      // …      // загружаем атрибуты в VBO     glNamedBufferStorage(_position_vbo,   a_position.size() * sizeof (float),   a_position.data(),  gl::GL_NONE_BIT);     // УДАЛЕНО // glNamedBufferStorage(_normal_vbo,     a_normal.size() * sizeof (float),     a_normal.data(),    gl::GL_NONE_BIT);     glNamedBufferStorage(_cell_index_vbo, a_index.size() * sizeof (float),      a_index.data(),     gl::GL_NONE_BIT);     glNamedBufferStorage(_texcoord_vbo,   a_texcoord.size() * sizeof (float),   a_texcoord.data(),  gl::GL_NONE_BIT);     glNamedBufferStorage(_property_vbo,   a_property.size() * sizeof (float),   a_property.data(),  gl::GL_NONE_BIT);

Затем избавимся от атрибута (придется сдвинуть номера последующих атрибутов):

void CornerPointGrid::_setup_vao() {     // создаем VAO     glCreateVertexArrays(1, &_vao);     // назначаем индексный буфер в VAO     glVertexArrayElementBuffer(_vao, _indexbuffer);      // назначаем все атрибуты в VAO     // position     glVertexArrayVertexBuffer(_vao, 0, _position_vbo, 0, sizeof (float) * 3);     glVertexArrayAttribBinding(_vao, 0, 0);     glVertexArrayAttribFormat(_vao, 0, 3, GL_FLOAT, GL_FALSE, 0);     glEnableVertexArrayAttrib(_vao, 0);      // normal     // УДАЛЕНО // glVertexArrayVertexBuffer(_vao, 1, _normal_vbo, 0, sizeof (float) * 3);     // УДАЛЕНО // glVertexArrayAttribBinding(_vao, 1, 1);     // УДАЛЕНО // glVertexArrayAttribFormat(_vao, 1, 3, GL_FLOAT, GL_FALSE, 0);     // УДАЛЕНО // glEnableVertexArrayAttrib(_vao, 1);      // cell index     glVertexArrayVertexBuffer(_vao, 1, _cell_index_vbo, 0, sizeof (float) * 3);     glVertexArrayAttribBinding(_vao, 1, 1);     glVertexArrayAttribFormat(_vao, 1, 3, GL_FLOAT, GL_FALSE, 0);     glEnableVertexArrayAttrib(_vao, 1);      // texcoord     glVertexArrayVertexBuffer(_vao, 2, _texcoord_vbo, 0, sizeof (float) * 2);     glVertexArrayAttribBinding(_vao, 2, 2);     glVertexArrayAttribFormat(_vao, 2, 2, GL_FLOAT, GL_FALSE, 0);     glEnableVertexArrayAttrib(_vao, 2);      // property     glVertexArrayVertexBuffer(_vao, 3, _property_vbo, 0, sizeof (float));     glVertexArrayAttribBinding(_vao, 3, 3);     glVertexArrayAttribFormat(_vao, 3, 1, GL_FLOAT, GL_FALSE, 0);     glEnableVertexArrayAttrib(_vao, 3);          //...

И, наконец, модифицируем шейдеры. В вершинном шейдере рассчитаем модельные координаты вершины и передадим их во фрагментный шейдер:

// …  // матрицы MVP-преобразования layout(location=0) uniform mat4 u_mvp; // матрица модели (для расчета нормали) layout(location=1) uniform mat4 u_model; // …   layout(location=0) out INTERFACE {     // цвет вершины     vec4 color;     // координаты ячейки в пространстве модели (для вычисления нормали)     vec3 model_pos;     // текстурные координаты     vec2 texcoord; } vs_out;  void main() {      // проводим mvp-преобразования позиции     vec4 pos = vec4(a_pos, 1);     gl_Position = u_mvp * pos;      // если делаем пикинг индексов ячеек, вместо цвета передаем во фрагментный шейдер индексы ячейки     if (u_primitive_picking) {         vs_out.color = vec4(a_ind.x, a_ind.y, a_ind.z, 1);         return;     }      // передаем координаты ячейки (для вычисления нормали)     vs_out.model_pos = vec3(u_model * pos);      // … }

Во фрагментном шейдере возьмём интерполированные при растеризации модельные координаты, получим их экранные производные и посчитаем нормаль как векторное произведение:

// …  layout(location = 0) in INTERFACE {     vec4 cell_color;     vec3 model_pos;     vec2 texcoord; } fs_in;  // …  void main() {     if (u_primitive_picking) {         FragColor = fs_in.cell_color;         return;     }      vec3 normal = normalize(cross(dFdy(fs_in.model_pos), dFdx(fs_in.model_pos)));     // … }

Если мы сделали всё правильно, мы не увидим особой разницы на простой сетке. Но на сетках с непланарными гранями разница станет очевидной:

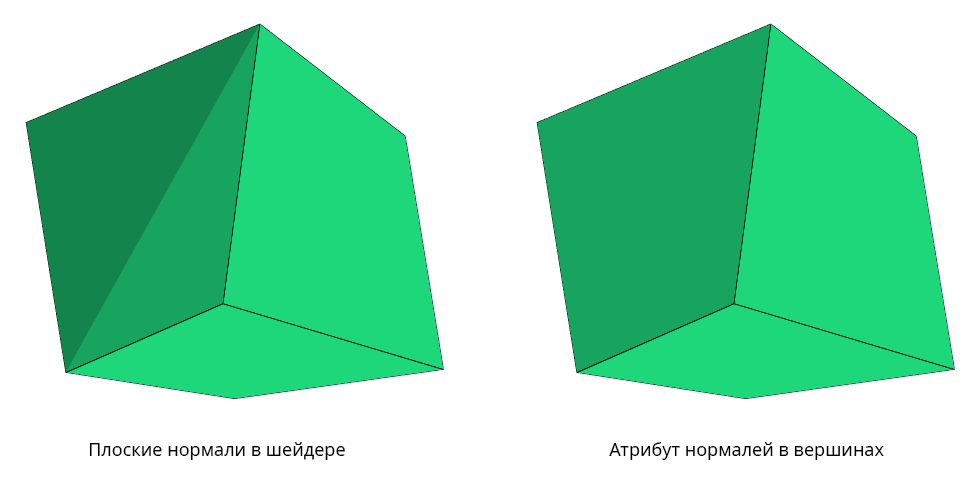
Рисунок 1 Сравнение плоских нормалей, рассчитанных шейдером, и реальных нормалей грани, заданных в атрибутах вершин

На реальных сетках месторождений разница не настолько заметна, поскольку обычно грани ячеек более-менее планарны.

Что же с потреблением памяти? 

Таблица 1 Сравнение потребления памяти и производительности на тестовой сетке размером 200³ c 50% активных ячеек на видеокарте AMD RX580 8GB

Как видим, объём потребляемой памяти предсказуемо уменьшился, а частота кадров немного увеличилась даже несмотря на то, что освещение теперь вычисляется во фрагментном шейдере.

После удаления атрибута нормалей список атрибутов выглядит следующим образом:

1.                  координаты вершины (3*4 байт);

2.                  индексы ячейки (3*4 байт);

3.                  текстурные координаты (2*4 байт);

4.                  значение свойства в ячейке (4 байта).

Обратим внимание на атрибут текстурных координат. Каждая компонента вектора текстурных координат принимает одно из двух значений: 0 или 1. Использовать целых восемь байт ради двух бит — расточительно, так что этот атрибут следующий в списке на расстрел оптимизацию.

Куда же запаковать эти два бита? Наилучшим кандидатом является атрибут индексов ячейки: индексы всегда положительны — так что мы можем записать по одному биту текстурной координаты в их знаки без потери информации.

Как и в случае с нормалями, сначала удалим из метода генерации вершин и шейдера все упоминания атрибута текстурных координат:

// … // УДАЛЕНО // std::vector<float> a_position, a_index, a_property, a_texcoord; std::vector<float> a_position, a_index, a_property; // для каждой вершины 3 координаты (x, y и z) a_position.reserve(3 * vertex_count); // + три индекса a_index.reserve(3 * vertex_count); // + значение свойства ячейки a_property.reserve(vertex_count); // УДАЛЕНО // + две текстурные координаты (расстояние от вершин до противолежащих сторон) // УДАЛЕНО // a_texcoord.reserve(2 * vertex_count);  // …  // загружаем атрибуты в VBO glNamedBufferStorage(_position_vbo,   a_position.size() * sizeof (float),  a_position.data(), gl::GL_NONE_BIT); glNamedBufferStorage(_cell_index_vbo, a_index.size() * sizeof (float),     a_index.data(),    gl::GL_NONE_BIT); // УДАЛЕНО //glNamedBufferStorage(_texcoord_vbo,   a_texcoord.size() * sizeof (float),  a_texcoord.data(), gl::GL_NONE_BIT); glNamedBufferStorage(_property_vbo,   a_property.size() * sizeof (float),  a_property.data(), gl::GL_NONE_BIT);  // …  // cell index glVertexArrayVertexBuffer(_vao, 1, _cell_index_vbo, 0, sizeof (float) * 3); glVertexArrayAttribBinding(_vao, 1, 1); glVertexArrayAttribFormat(_vao, 1, 3, GL_FLOAT, GL_FALSE, 0); glEnableVertexArrayAttrib(_vao, 1);  // texcoord // УДАЛЕНО //glVertexArrayVertexBuffer(_vao, 2, _texcoord_vbo, 0, sizeof (float) * 2); // УДАЛЕНО //glVertexArrayAttribBinding(_vao, 2, 2); // УДАЛЕНО //glVertexArrayAttribFormat(_vao, 2, 2, GL_FLOAT, GL_FALSE, 0); // УДАЛЕНО //glEnableVertexArrayAttrib(_vao, 2);  // property glVertexArrayVertexBuffer(_vao, 2, _property_vbo, 0, sizeof (float)); glVertexArrayAttribBinding(_vao, 2, 2); glVertexArrayAttribFormat(_vao, 2, 1, GL_FLOAT, GL_FALSE, 0); glEnableVertexArrayAttrib(_vao, 2);

Затем модифицируем массивы с описанием значений текстурных координат — там, где был 0, запишем -1:

// Для того, чтобы рисовать сетку на границах ячеек, // надо знать насколько близко расположен пиксель к границе. // Тут перечислены текстурные координаты для каждой вершины грани, // которые позволят получить расстояние до границы // (если один из компонентов равен нулю, то это и есть граница). static const std::array<vec2, 4> quad_vertices_texcoords = {     vec2( 1, -1),     vec2(-1, -1),     vec2(-1,  1),     vec2(-1, -1), };

И умножим первые две компоненты индекса ячейки на текстурные координаты — так записывается знак:

// …  // записываем атрибуты вершины a_position.insert(a_position.end(), {v.x, v.y, v.z}); // запишем текстурные координаты в знаки индексов ячейки. a_index.insert(a_index.end(), { i * texcoords[0],                                 j * texcoords[1],                                 k }); // …

После этого в вершинном шейдере восстановим значения индексов, просто взяв модуль, а текстурные координаты восстановим с помощью функции sign():

// …  // если делаем пикинг индексов ячеек, вместо цвета передаем во фрагментный шейдер индексы ячейки if (u_primitive_picking) {     vs_out.color = vec4(abs(a_ind.x), abs(a_ind.y), a_ind.z, 1);     return; }  // передаем координаты ячейки (для вычисления нормали) vs_out.model_pos = vec3(u_model * pos);  // передаем текстурные координаты в фрагментный шейдер vs_out.texcoord = vec2(max(vec2(0), sign(a_ind.xy)));

Запускаем и замеряем потребление памяти и производительность:

Таблица 2 Сравнение потребления памяти и производительности на видеокарте AMD RX580 8GB

Как и в случае с нормалями, потребление памяти сократилось, а частота кадров немного увеличилась.

Можно дополнительно уменьшить размер атрибута индексов ячейки, если хранить их не во float, а в int16 – сетки с числом ячеек более 32767 по одной из размерностей нам не встречались, не говоря уж о том, что такой огромный размер сетки не переварит ни одна рабочая станция.

Меняем тип данных индекса на int16 (придется сдвинуть индексы на 1, чтобы не потерять знак в нуле):

// … // УДАЛЕНО // std::vector<float> a_position, a_index, a_property; std::vector<float> a_position, a_property; std::vector<int16_t> a_index;  // …  // записываем атрибуты вершины a_position.insert(a_position.end(), {v.x, v.y, v.z}); // запишем текстурные координаты в знаки индексов ячейки. // прибавим 1 к индексу, чтобы знак не потерялся в нуле a_index.insert(a_index.end(), {static_cast<int16_t>((i+1) * texcoords[0]),                                static_cast<int16_t>((j+1) * texcoords[1]),                                static_cast<int16_t>(k) });  // …  // загружаем атрибуты в VBO glNamedBufferStorage(_position_vbo,    a_position.size() * sizeof (float), a_position.data(), gl::GL_NONE_BIT); glNamedBufferStorage(_cell_index_vbo, a_index.size() * sizeof (int16_t),  a_index.data(),    gl::GL_NONE_BIT); glNamedBufferStorage(_property_vbo,   a_property.size() * sizeof (float), a_property.data(), gl::GL_NONE_BIT);  // …  // назначаем все атрибуты в VAO // position glVertexArrayVertexBuffer(_vao, 0, _position_vbo, 0, sizeof (float) * 3); glVertexArrayAttribBinding(_vao, 0, 0); glVertexArrayAttribFormat(_vao, 0, 3, GL_FLOAT, GL_FALSE, 0); glEnableVertexArrayAttrib(_vao, 0);  // cell index glVertexArrayVertexBuffer(_vao, 1, _cell_index_vbo, 0, sizeof (int16_t) * 3); glVertexArrayAttribBinding(_vao, 1, 1); glVertexArrayAttribFormat(_vao, 1, 3, GL_SHORT, GL_FALSE, 0); glEnableVertexArrayAttrib(_vao, 1);

Запускаем, и…

Видим, что рендерер невероятно лагает — более 200 мс на кадр. Как же так?

Все дело в выравнивании атрибутов в памяти. Большинство видеокарт требуют, чтобы атрибут очередной вершины был выравнен по 32 битам. Очевидно, что наш атрибут с тремя компонентами из int16 выровнен всего лишь по 16 битам, что и приводит к неадекватной производительности. Решить проблему просто — добавим ещё одну компоненту для выравнивания:

// …  std::vector<float> a_position, a_property; std::vector<int16_t> a_index; // для каждой вершины 3 координаты (x, y и z) a_position.reserve(3 * vertex_count); // + три индекса (с выравниванием) a_index.reserve(4 * vertex_count); // …  // записываем атрибуты вершины a_position.insert(a_position.end(), {v.x, v.y, v.z}); // запишем текстурные координаты в знаки индексов ячейки. // прибавим 1 к индексу, чтобы знак не потерялся в нуле a_index.insert(a_index.end(), {static_cast<int16_t>((i+1) * texcoords[0]),                                static_cast<int16_t>((j+1) * texcoords[1]),                                static_cast<int16_t>(k),                                0});  // …  // назначаем все атрибуты в VAO // position glVertexArrayVertexBuffer(_vao, 0, _position_vbo, 0, sizeof (float) * 3); glVertexArrayAttribBinding(_vao, 0, 0); glVertexArrayAttribFormat(_vao, 0, 3, GL_FLOAT, GL_FALSE, 0); glEnableVertexArrayAttrib(_vao, 0);  // cell index glVertexArrayVertexBuffer(_vao, 1, _cell_index_vbo, 0, sizeof (int16_t) * 4); glVertexArrayAttribBinding(_vao, 1, 1); glVertexArrayAttribFormat(_vao, 1, 4, GL_SHORT, GL_FALSE, 0); glEnableVertexArrayAttrib(_vao, 1);  //…  // вершинный шейдер: #version 440  // позиция layout(location=0) in vec3 a_pos; // индекс ячейки layout(location=1) in ivec4 a_ind;  //…

Этот фикс вернул производительность к ожидаемой:

Таблица 3 Сравнение потребления памяти и производительности на видеокарте AMD RX580 8GB

Объём потребляемой памяти ещё немного сократился, а производительность немного увеличилась.

На этом этапе мы сделали все очевидные оптимизации атрибутов, и их итоговый список выглядит так:

1.                  координаты вершины (3*4 байт);

2.                  индексы ячейки * текстурные координаты (4*2 байт);

3.                  значение свойства в ячейке (4 байта).

Теперь каждая вершина занимает в памяти не 48 байт, а 24 байта – в два раза меньше! Общий объём потребляемой видеопамяти сократился в 1,8 раза.

Оптимизируем производительность в худшем случае

В таблицах сверху мы уже видели колонку «FPS в худшем случае». Что же это за случай, и почему всё так плохо?

На самом деле, чтобы увидеть этот «худший случай», достаточно всего лишь развернуть камеру и посмотреть на сетку с обратной стороны. Частота кадров сразу падает в 3 раза, что очень сильно раздражает пользователя.

Причина такого значительного падения производительности кроется в порядке растеризации. Видеокарты обязаны растеризовать треугольники последовательно (или так, что результат эквивалентен последовательному) — это важно для корректности блендинга. К тому же, число треугольников в сетке настолько велико, что параллельно их все растеризовать всё равно невозможно.

Однако порядок растеризации влияет не только на блендинг, но и быстродействие при рендеринге с включённым тестом глубины. Представим следующую ситуацию:

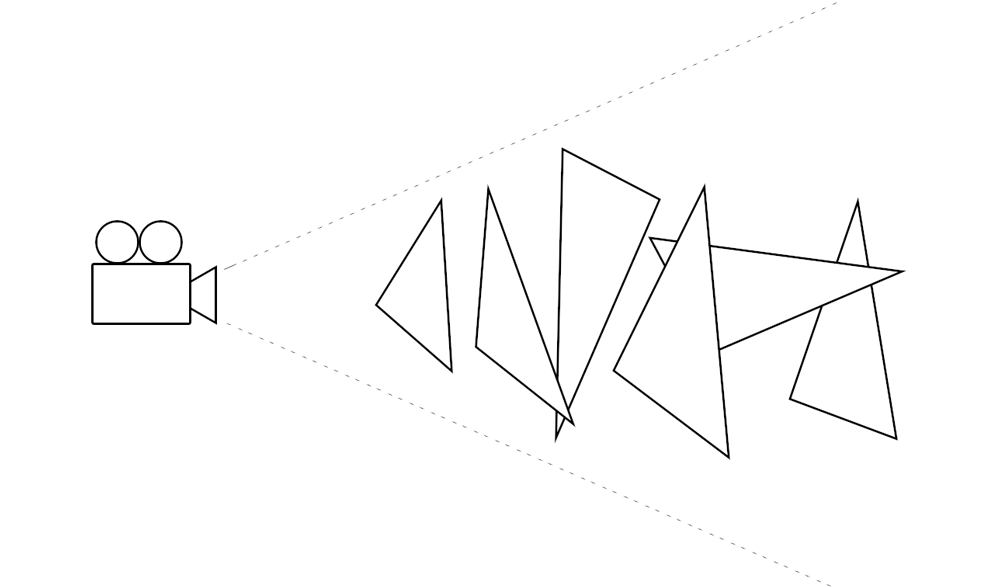
Рисунок 2. Перекрывающиеся треугольники

Рендерим несколько треугольников, которые с точки зрения камеры перекрывают друг друга.

Если с точки зрения камеры треугольники рендерятся в порядке от дальнего к ближнему, то каждый треугольник пройдёт тест глубины, и все его пиксели запишутся в фреймбуфер. Если же треугольники рендерятся в обратном порядке — от ближнего к дальнему с точки зрения камеры, то первый треугольник перекроет остальные в буфере глубины, а остальные треугольники не пройдут тест глубины и не будут записывать свои пиксели в фреймбуфер. Кроме того, на всех современных видеокартах реализована оптимизация Early Z Rejection, благодаря которой фрагментный шейдер даже не запускается для фрагментов, не прошедших тест глубины.

Вернёмся к нашему рендереру и вспомним, в каком порядке мы генерируем вершины:

// …  // для каждой рассматриваемой ячейки for (uint32_t i = 0; i < _property.ni; ++i) {     for (uint32_t j = 0; j < _property.nj; ++j) {         for (uint32_t k = 0; k < _property.nk; ++k) {              // если ячейка может отрисовываться (они фильтруются по маске)             if (_mask.at(i, j, k)){                 // …

Видно, что мы просто генерируем вершины ячеек в порядке их хранения в трёхмерном массиве.

Это объясняет, почему с одной стороны сетки частота кадров высокая, а с другой — низкая. Во втором случае мы просто смотрим на сетку с той стороны, в какую растут индексы ячеек — из-за этого каждая следующая грань находится ближе к камере, чем предыдущая, и всегда проходит тест глубины.

Решение этой проблемы тривиально — нужно всего лишь генерировать ячейки так, чтобы с любой возможной точки зрения камеры грани ячеек располагались в порядке от ближней к дальней. А для этого просто представим нашу сетку как луковицу — сначала сгенерируем все грани самого внешнего слоя, затем сгенерируем все грани следующего слоя и так далее, до самого центра луковицы.

Чтобы было проще закодить этот алгоритм, вынесем часть кода, отвечающую за генерацию граней одной ячейки, в лямбду:

// …  // + значение свойства ячейки a_property.reserve(vertex_count);  auto calc_cell = [this, &a_position, &a_index, &a_property](size_t i, size_t j, size_t k) {     // буфер, куда записываются вершины ячейки     std::array<vec3, 8> cell_vertices;       // если ячейка может отрисовываться (они фильтруются по маске)     if (_mask.at(i, j, k)){         // рассчитаем 8 вершин, соответствующих ячейке         get_cell_vertices(_coord, _zcorn, i, j, k, cell_vertices);         // … };

Затем напишем такой, страшный на вид, цикл:

size_t min_dim = std::min({_property.ni, _property.nj, _property.nk}); size_t max_layers = min_dim / 2 + 1;  size_t oi = 0, oj = 0, ok = 0; size_t ni = _property.ni, nj = _property.nj, nk = _property.nk;  for (size_t layer = 0; layer < max_layers; ++layer) {      for (size_t k : {ok, nk-1}) {         for (size_t i = oi; i < ni; ++i) {             for (size_t j = oj; j < nj; ++j) {                 calc_cell(i, j, k);             }         }         if (ok >= nk-1) break;     }      for (size_t j : {oj, nj-1}) {         for (size_t i = oi; i < ni; ++i) {             for (size_t k = ok+1; k < nk - 1; ++k) {                 calc_cell(i,j,k);             }         }         if (oj >= nj - 1) break;     }      for (size_t i : {oi, ni-1}) {         for (size_t j = oj+1; j < nj-1; ++j) {             for (size_t k = ok+1; k < nk-1; ++k) {                 calc_cell(i, j ,k);             }         }         if (oi >= ni - 1) break;     }       ++oi; ++oj; ++ok;     --ni; --nj; --nk; }

Наверняка есть много способов написать алгоритм, который обходит трёхмерный массив в луковичном порядке — здесь приведен самый простой, который придуман за 5 минут. Производительность этих циклов не имеет большого значения, т. к. каждая итерация (генерация граней) намного дороже, чем сами циклы.

Запускаем рендерер и видим, что частота кадров всегда высокая и практически не меняется, независимо от того, с какой стороны мы смотрим на сетку. Худший случай теперь работает в три раза быстрее, чем до оптимизации!

Таблица 4. Сравнение потребления памяти и производительности на видеокарте AMD RX580 8GB

Уменьшаем пиковое потребление оперативной памяти

В первой части мы обратили внимание на то, что вершины генерируются в промежуточные буферы в оперативной памяти и лишь затем передаются в буферы OpenGL. Это значит, что в худшем случае выделяется двойной объём памяти — одна копия в наших массивах, а вторая копия может выделяться драйвером перед передачей в видеопамять.

Для решения этой проблемы ещё в OpenGL 1.5 была добавлена возможность сделать память буфера видимой в адресном пространстве процесса с помощью функции glMapBuffer(). Эта функция возвращает указатель, по которому можно писать или читать данные буфера «напрямую». В случае современных интегрированных видеокарт, это мало чем отличается от работы с обычной оперативной памятью (однако, для старших поколений интегрированных видеокарт это не всегда так). Для дискретных видеокарт механизм работы с такой памятью обычно зависит от специфики конкретной модели видеокарты и версии драйвера и не документирован.

Избавляемся от промежуточных массивов и сохраняем атрибуты вершин по указателям, полученным через glMapBuffer():

void CornerPointGrid::_gen_vertices_and_indices(size_t quad_count) {      const size_t vertex_count = quad_count * 4;      // загружаем атрибуты в VBO     glNamedBufferStorage(_position_vbo,   3 * vertex_count * sizeof (float),   nullptr, gl::GL_MAP_WRITE_BIT);     glNamedBufferStorage(_cell_index_vbo, 4 * vertex_count * sizeof (int16_t), nullptr, gl::GL_MAP_WRITE_BIT);     glNamedBufferStorage(_property_vbo,   vertex_count * sizeof (float),       nullptr, gl::GL_MAP_WRITE_BIT);      auto a_position = reinterpret_cast<float*>(glMapNamedBuffer(_position_vbo,     gl::GL_WRITE_ONLY));     auto a_index    = reinterpret_cast<int16_t*>(glMapNamedBuffer(_cell_index_vbo, gl::GL_WRITE_ONLY));     auto a_property = reinterpret_cast<float*>(glMapNamedBuffer(_property_vbo,     gl::GL_WRITE_ONLY));      // …      // для каждой вершины в полигоне     for (int vii = 0; vii < 4; ++vii){              // координаты очередной вершины         const vec3& v = cell_vertices[quad[vii]];         ivec2 texcoords = quad_vertices_texcoords[vii];          // записываем атрибуты вершины         a_position[0] = v.x;         a_position[1] = v.y;         a_position[2] = v.z;         a_position += 3;         // запишем текстурные координаты в знаки индексов ячейки.         // прибавим 1 к индексу, чтобы знак не потерялся в нуле         a_index[0] = static_cast<int16_t>((i+1) * texcoords[0]);         a_index[1] = static_cast<int16_t>((j+1) * texcoords[1]);         a_index[2] = static_cast<int16_t>(k);         a_index[3] = 0;         a_index += 4;          a_property[0] = _property.at(i, j, k);         a_property += 1;     }

То же самое делаем и с индексами:

// …  // создадим массив индексов - на каждую грань два треугольника size_t indices_count = quad_count * 6; glNamedBufferStorage(_indexbuffer, indices_count * sizeof (uint32_t), nullptr, gl::GL_MAP_WRITE_BIT); auto indices = reinterpret_cast<uint32_t*>(glMapNamedBuffer(_indexbuffer, gl::GL_WRITE_ONLY));  for (size_t i = 0; i < quad_count; ++i)     for (uint32_t j = 0; j < 6; ++j)         // индекс очередной вершины при составлении треугольников         *indices++ = static_cast<uint32_t>(i * 4 + quad_to_triangles[j]);  glUnmapNamedBuffer(_indexbuffer); glUnmapNamedBuffer(_position_vbo); glUnmapNamedBuffer(_cell_index_vbo); glUnmapNamedBuffer(_property_vbo);  // …

Убедившись, что всё работает как надо, проверим пиковое потребление оперативной памяти:

Таблица 5. Сравнение потребления памяти на видеокарте AMD RX580 8GB

Видим, что пиковое потребление памяти процессом значительно уменьшилось, что позволяет быстро загружать большие сетки на одной и той же машине.

Неожиданная проблема

На этом мы планировали поставить точку, однако при тестировании на нескольких видеокартах Nvidia разных моделей и поколений (GTX 1050Ti, RTX 2070) обнаружилась весьма необычная проблема — производительность катастрофически упала до 400+ мс на кадр. С помощью git bisect мы определили, что проблема возникла именно после последней оптимизации с glMapBuffer(). Странным было и то, что на продакшн-версии движка эта проблема не воспроизводилась, как и на видеокартах AMD и Intel.

В отладочном выводе (GL_KHR_debug) были сразу замечены такие строки:

Buffer detailed info: Buffer object 1 (bound to NONE, usage hint is GL_DYNAMIC_DRAW) will use SYSTEM HEAP memory as the source for buffer object operations. Buffer detailed info: Buffer object 1 (bound to NONE, usage hint is GL_DYNAMIC_DRAW) has been mapped WRITE_ONLY in SYSTEM HEAP memory (fast). …

Судя по логу, драйвер решил, что раз буфер создан с флагом GL_DYNAMIC_DRAW, то не нужно выделять под него видеопамять, ведь он всё равно будет очень часто перезаписываться. Вместо этого под буфер выделена обычная оперативная память, что и объясняет настолько низкую производительность.

Проблема в том, что мы нигде не указывали GL_DYNAMIC_DRAW – у нас даже нет такой возможности, ведь мы использовали glBufferStorage(), у которого такого флага нет.

Для эксперимента мы переделали выделение памяти в буфере на устаревший glBufferData(…, GL_STATIC_DRAW), после чего проблема с производительностью исчезла, а в логе появились такие сообщения:

Buffer detailed info: Buffer object 1 (bound to NONE, usage hint is GL_STATIC_DRAW) will use VIDEO memory as the source for buffer object operations. Buffer detailed info: Buffer object 1 (bound to NONE, usage hint is GL_STATIC_DRAW) has been mapped in HOST memory …

Насколько мы можем судить, подсказки использования буферов драйвер Nvidia воспринимает слишком буквально – в нашем случае GL_DYNAMIC_DRAW оказался неудачным значением по умолчанию. Не стоит сильно их винить, поскольку это в большей степени недоработка спецификации GL_ARB_buffer_storage, не предвидевшей возможные проблемы из-за сохранения обратной совместимости со старым способом выделения памяти.

Бенчмарк

Сравним производительность рендерера до и после оптимизации на нескольких моделях видеокарт:

Таблица 6. Сравнение производительности до и после оптимизаций

На протестированных видеокартах прирост производительности составил около 30% для хорошего случая, а для худшего случая – от 80% до 410%!

Заключение

В этой статье мы рассмотрели несколько оптимизаций рендерера угловой геометрии, которые снизили объём потребляемой видеопамяти почти в два раза и увеличили частоту кадров в три с лишним раза. Теперь наш рендерер сможет отобразить сетки большего размера на маломощных офисных машинах и сетки размером порядка миллиарда ячеек на рабочих станциях.

Конечно, это не все возможные оптимизации — например, можно ещё уменьшить размер атрибутов, наложив некоторые ограничения на входные данные. Можно улучшить алгоритм отсечения невидимых граней, о котором упоминалось в первой части статьи; можно уменьшить число уникальных вершин при генерации граней одной ячейки; можно генерировать вершины не разом, а чанками… Для примера, продакшн-версия движка, где мы реализовали подобные оптимизации, потребляет ещё в полтора раза меньше памяти, а по сравнению с изначальной реализацией — почти в четыре раза меньше памяти!

На этом мы заканчиваем цикл статей о рендеринге угловой геометрии. Надеемся, что обе части оказались интересными и полезными. В комментариях ждем ваших вопросов; будем рады обсудить описанные и новые способы оптимизации рендерера!