Заберите свои скобки

Возможно, вы слышали о том, как удобно в функциональных языках программирования стыковать функции между собой. К сожалению, это не всегда так, и порой нам надо выбирать между понятным и коротким кодом. В этой заметке мы познакомимся с бесточечным стилем, понятием ассоциативности и старшинства для операторов и попробуем полностью избавиться от скобок.

В большинстве современных языков программирования скобки используются в качестве оператора применения функции к ее аргументам:

q (x, y z)

Но в Haskell оператор применения функции — это обычный пробел:

q :: a -> b -> c -> d x :: a y :: b z :: y  q x y z

Подождите-ка, мы применяем функцию f к аргументам, а пробелов намного больше! Значит ли это, что у нас тут несколько применений функции к аргументам? Да:

(((q x) y) z)

Мы получаем несколько применений функции в каррированной форме:

q x :: b -> c -> d q x y :: c -> d q x y z :: d

Значит ли это, что мы можем отказаться от скобок? Нет, потому что в качестве аргументов нам могут попадаться применения функций, нам может быть просто лень придумывать новое имя для выражения, которое будет лишь промежуточным шагом:

q :: a -> b -> c -> d p :: b -> c  q x y (p y)

И вот тут без скобочек нам не обойтись, потому что иначе проверка типов будет считать, что мы подаем на вход функции f два разных аргумента:

q :: a -> b -> (b -> c) -> b -> ???  q x y p y

К счастью, у нас уже есть инфиксный оператор в базовой библиотеке, который поможет нам избавиться от ненужных скобок:

q :: a -> b -> c -> d p :: b -> c  q x y $ p y

Этот оператор ($) обычно называют применением — мы всего лишь явно отделяем функцию от аргумента, который нужен ей для получения результата.

Одной функции никогда не бывает достаточно, и мы хотим применить другую, но уже вкусив код без скобочек, хочется просто написать: 

($) :: a -> (a -> b) -> b o :: d -> e  o (q x y $ p y) === o $ q x y $ p y

Неплохо выглядит! Но что, если вместо того, чтобы явно подавать аргументы для их последующего скармливания функциям, мы будем соединять функции между собой без какого-либо упоминания аргументов? Вы, наверное, уже видели эту диаграмму, когда читали статьи о функциональном программировании: 

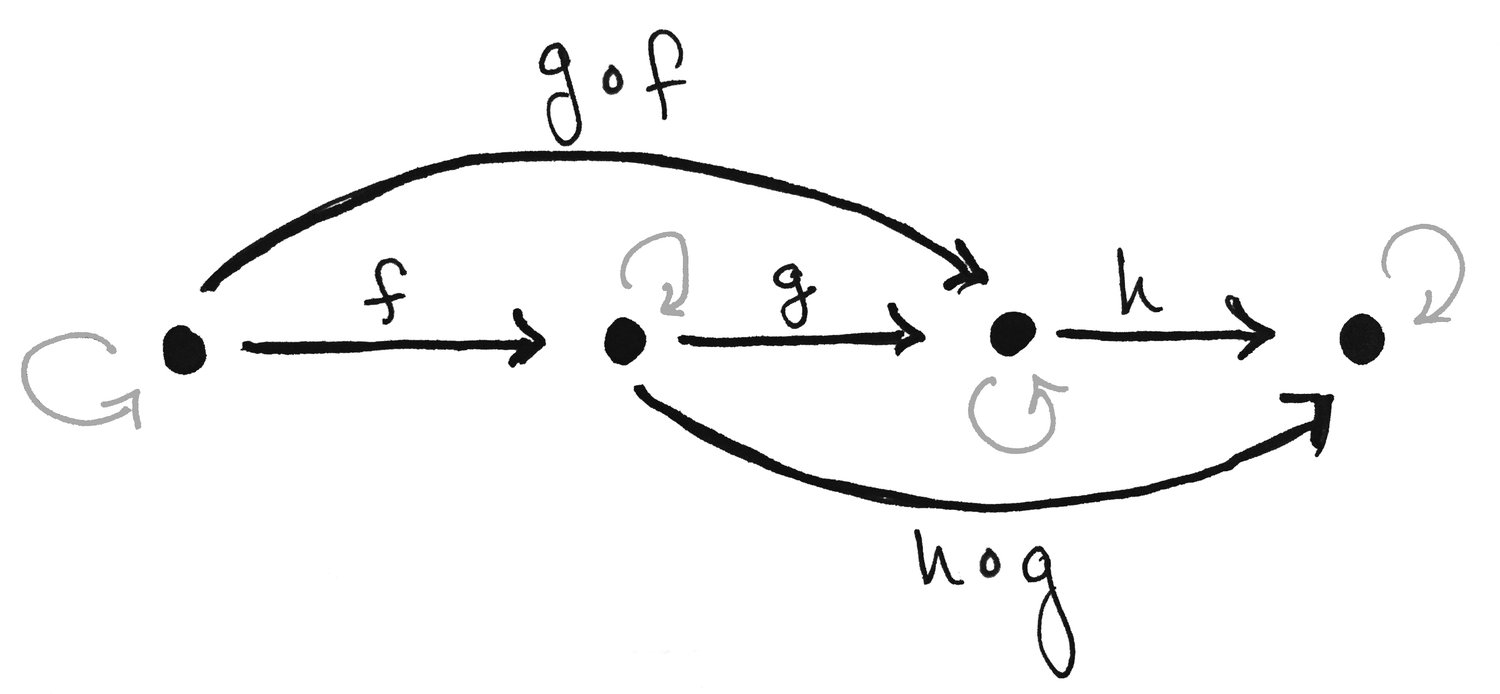
«What is a Category? Definition and Examples» (c) Math3ma

Композиция — суть теории категорий, поэтому у нас уже давно есть способ объединять функции в ассоциативную цепочку. Еще такую запись принято называть бесточечной нотацией (несмотря на то, что точек явно в такой записи больше):

f :: a -> b g :: b -> c g . f :: a -> c  (.) :: (b -> c) -> (a -> b) -> (a -> c)  g (f x) === g . f

Зачастую вопрос о том, использовать ли композицию или применение — стилистический, так как эти два представления приводят к одному и тому же результату:

g . f === g $ f x

Если у нас в выражении есть где-то свободная переменная, мы можем применить ее с помощью одного оператора применения, а дальше использовать композицию (я в большинстве случаев именно так и делаю). Да и код читается намного лучше:

j $ h $ f $ g $ x === j . h . f . g $ x

Но с этими двумя операторами есть одна проблема — они умеют принимать только по одному аргументу. Если в качестве аргументов функции выступают другие объемные выражения, без скобок не обойтись:

f :: a -> b -> c g :: a -> b -> c -> d h :: c -> d -> e  h (f x y) (g x y z)

Можно убрать лишь скобки справа:

h (f x y) (g x y z) === h (f x y) $ g x y z

Как убрать скобки слева? Чтобы понять, как подступиться к этой проблеме, давайте разберем композицию (.) и применение ($). Оба эти оператора — правоассоциативные. Ассоциативность — это про скобки. Ассоциативность справа — значит скобки группируются справа.

f . g . h === f $ g $ h x === f (g (h x))

Так как в Haskell функции уже в каррированной форме, мы не обязаны подавать все аргументы сразу — мы можем подавать их по одному.

f :: a -> b -> c -> d f x :: b -> c -> d f x y :: c -> d f x y z :: d

Выходит, если мы хотим придумать такой оператор, который мог бы принимать несколько операндов, нам надо сделать его левоасcоциативным, чтобы он мог принимать операнды по-одному справа налево: 

(???) :: (a -> b -> c -> ...) -> a -> b -> c -> ... ((??? x) y) z) ...

Мы можем взять какую-нибудь часто используемую функцию, чтобы на ней протестировать наш новый оператор. Например, обработчик опциональной ошибки:

maybe :: b -> (a -> b) -> Maybe a -> b

Давайте выберем для нашего нового оператора какой-нибудь ASCII-символ, который еще вроде никак не используется в базовой библиотеке.

(#) :: (a -> b -> c -> ...) -> a -> b -> c -> ... f # x y z ... = ???

Кроме ассоциативности, для оператора нужно выбрать старшинство — это номер от 0 до 9, который определяет приоритет операторов. Чем выше номер, тем ниже приоритет. Например: 

infixr 9 . infixr 0 $

Именно поэтому мы группируем скобки вокруг $, а не .:

h . g . f $ x === (h . (g . f)) $ (x)

В общем, для нашего нового оператора мы вольны выбрать любое число между 0 и 9. Давайте выберем что-нибудь среднее — 5.

infixl 5 #

Но как нам его написать? На самом деле, это тоже оператор применения, только сфокусированный на функции, а не на аргументах: 

f # x = f x

Эмм… и как это работает? Рассмотрим лучше на каком-нибудь примере — пусть это будет тот же обработчик опциональной ошибки. Так как функции уже находятся в каррированной форме, мы можем скармливать аргументы один за другим:

maybe :: b -> (a -> b) -> Maybe a -> b maybe x :: (a -> b) -> Maybe a -> b maybe x f :: Maybe a -> b maybe x f ma :: b

Каррирование… отлично, значит, мы можем группировать скобки слева!

maybe # x # f # ma === ((maybe # x) # f) # ma  maybe # "undefined" # show . even # Just 1 === "False" maybe # "undefined" # show . even # Just 2 === "True" maybe # "undefined" # show . even # Nothing === "undefined"

Если применяемые аргументы достаточно большие и нет особой надобности в том, чтобы придумывать им имена, мы можем выстроить их в такой блок с отступом:

string_or_int :: Either String Int either :: (a -> c) -> (b -> c) -> Either a b -> c  either  	 # print . ("String: " <>)  	 # print . ("Int: " <>) . show 	 # string_or_int

Я пока что нигде еще не видел такого оператора, но мне бы он сильно понадобился там, где не справляются $ и .. Напишите в комментариях, если подобное уже где-то существует, но по какой-то причине отсутсвует в base.