Меши с Python & Blender: кубы и матрицы

Это вторая часть серии, первая лежит тут.

В этой части Диего мало рассказывает о кубах, зато много — о том, как Блендер обрабатывает позицию объекта.

Добро пожаловать во второй туториал! Окунёмся в математику, поймём, как работать с масштабом, локацией и прочими изменениями меша в пространстве.

Происходящее в этой части базируется на первой, поэтому если где-то закипит мозг, попробуйте посмотреть в первый туториал. Сегодня мы займёмся кубиками, потом трансформациями объектов в пространстве, а в финале копнём в матрицы.

Подготовка

Подгрузим необходимые модули: как обычно, потребуется bpy, кроме того, radians() из модуля math, и Matrix из mathutilus — ещё одного модуля Блендера.

import bpy import math from mathutils import Matrix

Как и раньше, я записываю переменные в отдельный блок, потом делаю блок с функциями, и в конце блок с основных кодом. Функция vert() пока бессмысленна, но она скоро пригодится.

# ----------------------------------------------------------------------------- # Настройки name = 'Cubert'  # ----------------------------------------------------------------------------- # Функции  def vert(x,y,z):     """ Создаём вертекс """      return (x, y, z)   # ----------------------------------------------------------------------------- # Кубокод  verts = [] faces = []   # ----------------------------------------------------------------------------- # Добавляем объект в сцену  mesh = bpy.data.meshes.new(name) mesh.from_pydata(verts, [], faces)  obj = bpy.data.objects.new(name, mesh) bpy.context.scene.collection.objects.link(obj)  bpy.context.view_layer.objects.active = obj obj.select = True

выделение объекта…

…в версиях старше 2.79 реализовано так: obj.select_set(True)

Делаем кубик

Поскольку красивой функции для описания куба не существует, придётся вбить значения для него ручками. Но нас посетила удача: всего-то шесть граней да восемь вершин.

существует, но…

если мы задались целью просто бахнуть кубик, вероятно, влупить значения вручную будет действительно проще.

verts = [vert(1.0, 1.0, -1.0),          vert(1.0, -1.0, -1.0),          vert(-1.0, -1.0, -1.0),          vert(-1.0, 1.0, -1.0),          vert(1.0, 1.0, 1.0),          vert(1.0, -1.0, 1.0),          vert(-1.0, -1.0, 1.0),          vert(-1.0, 1.0, 1.0)]  faces = [(0, 1, 2, 3),          (4, 7, 6, 5),          (0, 4, 5, 1),          (1, 5, 6, 2),          (2, 6, 7, 3),          (4, 0, 3, 7)]

Запустите скприт, и полюбуйтесь результатом. Это было несложно, а теперь попробуем с ним что-нибудь сделать.

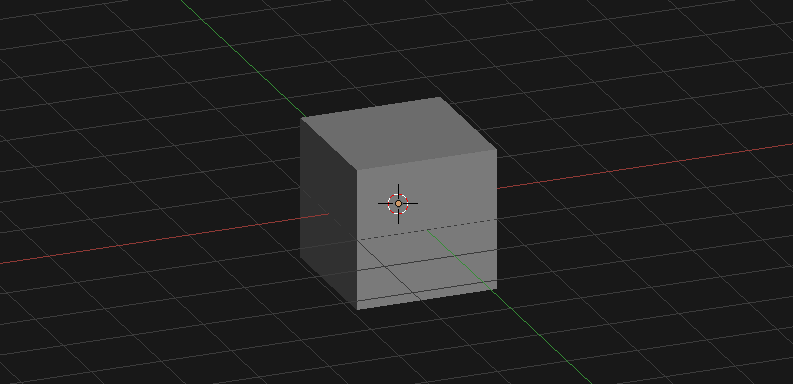
Центр объекта

У каждого объекта есть центральная точка, и её координаты характеризуют положение объекта в пространстве. То есть, когда мы говорим про координаты объекта, на самом деле мы говорим про координаты его центральной точки. Ну и меш располагается не в глобальных координатах, а относительно центральной точки объекта.

Звучит странновато? Вот иллюстрация:

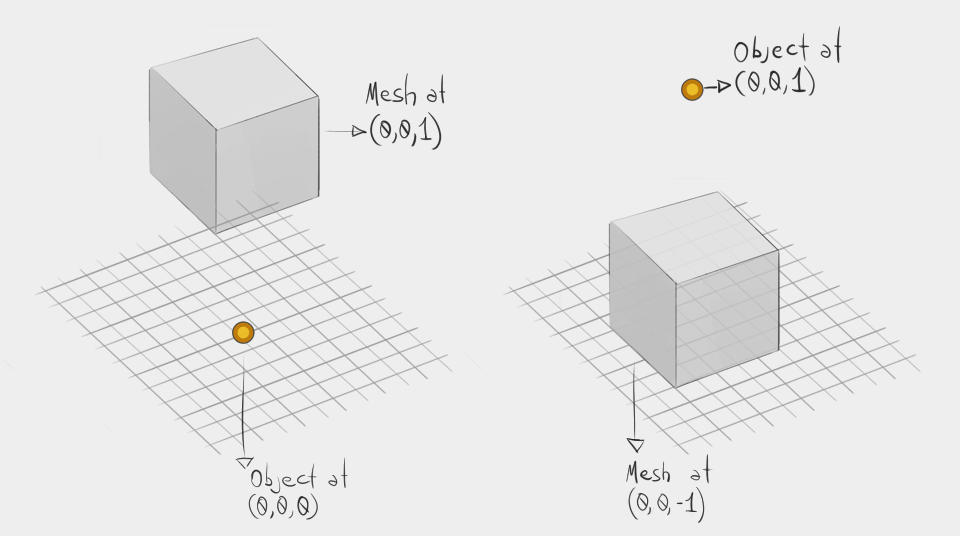
Оранжевая точка, она же центр объекта, располагается на координатной сетке, и имеет нулевые координаты, а во втором случае поднята по оси Z на единицу. При этом любопытно происходящее с мешем: в обоих случаях он смещён по Z на единицу, во втором случае — на минус единицу. Если бы его координаты были нулевыми, он бы располагался на сетке в первом случае, и поднялся бы над ней во втором случае. То есть в обоих случаях располагался бы возле центра объекта. Таким образом: расположение меша привязано к центру объекта, но не зависит от места самого объекта.

С этим знанием мы можем сделать две вещи:

изменить расположение меша относительно объекта. То же самое, что проиходит в режиме редактирования.
изменить локацию центра объекта. Меш останется в глобальных нулевых координатах, центре мира, так сказать.

Начнём с меша, а я продолжу называть эту операцию смещением.

offset = (0, 0, 1)  def vert(x,y,z):     """ Создаём вершинку """      return (x + offset[0], y + offset[1], z + offset[2])

Допишем переменную, определяющую смещение, и воткнём её в функцию, считающую координаты вершин.

Смещение по оси Z приподнимет кубик до центра объекта и координатной плоскости.

А теперь перенесём центр объекта, оставив меш в том же месте. Но мы не можем перемещать центр объекта напрямую, так как его координаты — суть координаты самого объекта.

Сделаем хитро: сместим координаты объекта, а координаты вертексов изменим на противоположное значение.

obj.location = [i * -1 for i in offset]

Положение — кортеж из трёх координат, так что нужно вычислить каждую отдельно.

Запустим код ещё раз. Куб вернулся в центр сцены, но визуализация центра объекта, да и сам объект сместились вниз, на позицию (0, 0, ‑1).

Поскольку смещение меша положительное, объект получает отрицательную координату. Соответсвтенно, если сместить меш в минус, центр объекта, наоборот, поднимеся. Попробуйте такое смещение:

offset = (0, 0, -5)

Как быть, если мы хотим изменить и позицию объекта, и позицию меша? Понадобится ещё одна переменная для смещения, которую мы сможем положить в координаты меша. Чутка всё перепишем, заодно приведём в порядок код:

origin_offset = (0, 0, -5) mesh_offset = (1, 0, 0)  def vert(x,y,z):     """ Создаём вершинку """      return (x + origin_offset[0], y + origin_offset[1], z + origin_offset[2])   obj.location = [(i * -1) + mesh_offset[j] for j, i in enumerate(origin_offset)]

Заметьте, что для прохода по списку мы используем не range(), а enumerate().

Можно ещё поиграться с vert(), но настало время узнать о другом способе работать с мешами и объектами в пространстве. Способе, который быстрее и удобнее.

Встречайте матрицы.

Матрицы.

В математике матрица — прямоугольная таблица из чисел (и иногда других элементов). Матрицы складываются, вычитаются друг из друга, умножаются. Везде, где вы найдёте математику, вы наверняка встретите и матрицы.

Ну, а поскольку мы здесь собрались ради компьютерной графики, матрицы нас заботят в качестве сущностей, определяющих положение объектов в пространстве: вращение, мастштабирование, перемещение. Матрицы для трансформации объектов называются матрицами линейных преобразований.

Поворот, масштаб и положение объекта определено матрицами в зависимости от системы координат. Даже если транформаций с объектом ещё не происходило, у объекта есть матрица World Matrix.

Вообразим какой-нибудь объект. Его координаты — (0, 0, 0), масштаб 1:1, а повёрнут он на ноль градусов по всем осям. Во-первых, эти данные хранятся в матрице, а во-вторых — эта матрица — нулевые координаты сцены, относительно которых происходят преобразования остальных объектов, а в третьих — она-то есть World Matrix.

Координаты сцены и есть глобальные координаты в Блендере. Существуют другие координатные пространства, но про них мы поговорим позже.

Для работы с матрицами не обазательно супер-хорошо понимать, что это: разработчики Блендера придумали класс Matrix, который выполняет большую часть работы вместо нас. Возможно, вы даже не увидите матрицы вовсе. Если математика не интересна, можно сразу перейти к разделу «Соберём всё в кучу«.

Если вы ещё здесь, предлагаю поиграть с самой идеей матриц. Добавим какой-нибудь объект комбинацией клавиш Ctrl+A. Выделим его, копипастнем и запустим скрипт ниже.

import bpy  print('-' * 80) print('World Matrix \n', bpy.context.object.matrix_world)

А вот что появится в терминале:

-------------------------------------------------------------------------------- World Matrix <Matrix 4x4 (1.0000, 0.0000, 0.0000, 0.0000)             (0.0000, 1.0000, 0.0000, 0.0000)             (0.0000, 0.0000, 1.0000, 0.0000)             (0.0000, 0.0000, 0.0000, 1.0000)>

Пока объект остаётся на месте, его матрица будет как у «воображаемого» объекта. Матрицы типа такой (нули и диагональ из единиц) математики называют единичными матрицами. Это нулевое состояние объекта: он не повёрнут, находится в нулях глобальных координат, и имеет свой родной масштаб.

Теперь подвигаем объект куда-нибудь, и снова запустим скрипт.

-------------------------------------------------------------------------------- World Matrix <Matrix 4x4 (1.0000, 0.0000, 0.0000, -8.8360)             (0.0000, 1.0000, 0.0000, -1.1350)             (0.0000, 0.0000, 1.0000,  8.9390)             (0.0000, 0.0000, 0.0000,  1.0000)>

Значения матрицы изменятся в зависимости от того, куда вы переместили объект. Последняя колонка содержит в себе X, Y и Z координаты объекта.

Сбросим перемещение хоткеем Alt+G, и поменяем объекту масштаб:

-------------------------------------------------------------------------------- World Matrix <Matrix 4x4 (0.7280,  0.0000, 0.0000, 0.0000)             (0.0000, -1.4031, 0.0000, 0.0000)             (0.0000,  0.0000, 1.7441, 0.0000)             (0.0000,  0.0000, 0.0000, 1.0000)>

Теперь в последней колонке нули, но поменялись значения в диагонали: так же по X, Y и Z.

C поворотом сложнее, так как поворот по одной оси тянет за собой изменения на двух других. Поворот за пределами нашего туториала, но для любителей математики я оставлю в конце пару ссылок.

-------------------------------------------------------------------------------- World Matrix <Matrix 4x4 (-0.9182,  0.3398, -0.2037, 0.0000)             (-0.2168, -0.8612, -0.4597, 0.0000)             (-0.3316, -0.3780,  0.8644, 0.0000)             ( 0.0000,  0.0000,  0.0000, 1.0000)>

Вам может быть любопытно, зачем четвёртая строка? Прямо говоря, матрицы для преобразований трёхмерного пространства на самом делё четырёхмерны. Это хитрость, позволяющая матрице работать в трёхмерном мире для комплексных изменений. Не буду вдаваться в детали, но оставлю ещё ссылок, описывающих происходящее. А прямо сейчас не важно: эта строка не планирует меняться.

Вот картинка, описывающая различные трансформации объекта:

Использование матриц

Матрицы трансформации могут собраться в одну супер-матрицу, учитывающую все изменения объекта. Если мы возьмём матрицу мира и умножим её на матрицу трансформаций объекта, получим новую, меняющую параметры объекта.

Ну, или сделаем это кодом:

obj.matrix_world @= some_transformation_matrix

Достанем импортированный класс Matrix, и посмотрим, как его использовать для создания матриц.

Перемещение

Самое — простое перемещать объекты! Нам понадобится метод Translation с вектором (кортежем) значений для каждой оси.

translation_matrix = Matrix.Translation((0, 0, 2)) obj.matrix_world @= translation_matrix

Масштабирование

Требует трёх аргументов. Первый — коэффициент масштабирования. Второй — размер матрицы, он может быть как 2 (2х2), так и 4 (4х4). Но поскольку мы работаем с трёхмерными объектами, размер матрицы всегда будет равен четырём. Третий аргумент объясняет, будет ли масштабирование вообще, и по какой оси. Если ноль — не будет, а если единица — будет.

scale_matrix = Matrix.Scale(2, 4, (0, 0, 1)) # Scale by 2 on Z obj.matrix_world @= scale_matrix

Поворот

Для поворота аргументы похожи на аргументы масштабирования. Первый будет углом поворота в радианах, второй так же размером матрицы, а третий осью вращения. Задать ось можно как вектором, так и строкой, типа ‘X’, ‘Y’ или ‘Z’.

rotation_mat = Matrix.Rotation(math.radians(20), 4, 'X') obj.matrix_world @= rotation_mat

Соберём всё в кучу

Мы можем применить все трансформации друг за другом, перемножив матрицы. Но важно соблюдать порядок, иначе результат будет странным. Сначала перемещение, потом вращение, а потом масштабирование. Если что-то пошло не по плану, первым делом посмотрите на порядок, в котором вы это делали.

translation = (0, 0, 2) scale_factor = 2 scale_axis = (0, 0, 1) rotation_angle = math.radians(20) rotation_axis = 'X'  translation_matrix = Matrix.Translation(translation) scale_matrix = Matrix.Scale(scale_factor, 4, scale_axis) rotation_mat = Matrix.Rotation(rotation_angle, 4, rotation_axis)  obj.matrix_world @= translation_matrix @ rotation_mat @ scale_matrix

Матрицы могут трансформировать сам меш. Всё, что понадобится для этого — transform() :

obj.data.transform(Matrix.Translation(translation))

Матрицы комбинируются умножением, преобразуя несколько параметров за один проход.

obj.data.transform(translation_matrix @ scale_matrix)

Matrix реализован на C, поэтому он быстрее варианта с переписыванием координат каждой вершинки. А ещё это всего одна строчка кода!

Прекрасно!

Финальный код

import bpy import math from mathutils import Matrix  # ----------------------------------------------------------------------------- # Настройки  name = 'Cubert'  # Origin point transformation settings mesh_offset = (0, 0, 0) origin_offset = (0, 0, 0)  # Matrices settings translation = (0, 0, 0) scale_factor = 1 scale_axis = (1, 1, 1) rotation_angle = math.radians(0) rotation_axis = 'X'   # ----------------------------------------------------------------------------- # Функции  def vert(x,y,z):     """ Make a vertex """      return (x + origin_offset[0], y + origin_offset[1], z + origin_offset[2])   # ----------------------------------------------------------------------------- # Кубокод  verts = [vert(1.0, 1.0, -1.0),          vert(1.0, -1.0, -1.0),          vert(-1.0, -1.0, -1.0),          vert(-1.0, 1.0, -1.0),          vert(1.0, 1.0, 1.0),          vert(1.0, -1.0, 1.0),          vert(-1.0, -1.0, 1.0),          vert(-1.0, 1.0, 1.0)]   faces = [(0, 1, 2, 3),          (4, 7, 6, 5),          (0, 4, 5, 1),          (1, 5, 6, 2),          (2, 6, 7, 3),          (4, 0, 3, 7)]   # ----------------------------------------------------------------------------- # Добавляем объект в сцену  mesh = bpy.data.meshes.new(name) mesh.from_pydata(verts, [], faces)  obj = bpy.data.objects.new(name, mesh) bpy.context.scene.collection.objects.link(obj)  bpy.context.view_layer.objects.active = obj obj.select = True  # ----------------------------------------------------------------------------- # Перемещаем меш, перемещая центральную точку  obj.location = [(i * -1) + mesh_offset[j] for j, i in enumerate(origin_offset)]   # ----------------------------------------------------------------------------- # Волшебство матриц  translation_matrix = Matrix.Translation(translation) scale_matrix = Matrix.Scale(scale_factor, 4, scale_axis) rotation_mat = Matrix.Rotation(rotation_angle, 4, rotation_axis)  obj.matrix_world @= translation_matrix @ rotation_mat @ scale_matrix   # ----------------------------------------------------------------------------- # Волшебство матриц (для меша)  # Сними решётку с нижней строки, чтобы погрузиться в него # obj.data.transform(translation_matrix @ scale_matrix)

Заключение

Несколько ссылок с возрастающей сложностью про матрицы:

Пара вещей, на которых можно потренироваться:

Сделайте цикл из этого кода, так, чтобы несколько кубиков расположились типа волны, или хитро повернулись.
Воспользуйтесь матрицами для перемещения центра объекта
Попробуйте отмасштабировать объект без матриц и координат объекта (вам пригодится функция vert())
Попробуйте применить матрицу одного объекта к другому.

В следующем туториале займёмся икосаэдром, и аппроскимацией его до состояния шара.

Оригинал статьи (автор не прикрутил к сайту сертификат, браузер может ругаться.)

Первая часть: меши с Python & Blender: двумерная сетка

ссылка на оригинал статьи https://habr.com/ru/post/647063/