Проблемы искусственного интеллекта и алгоритм лечения

Хотя обсуждаемые темы имеют и академический интерес, в настоящем сообщении приводится информация только для операционной деятельности.

Существуют многочисленные экспериментальные подтверждения лавинообразного характера сигнала в биологической нейронной сети. В коллективном сигнале, который обрабатывает мозг, нейроны уже «обезличены» по отношению к органам чувств и индивидуальным модам. Представляется важным отметить следующий факт: мозг обучается не на совокупности отдельных нейронов, а на особом коллективном состоянии нейронов. С потерей лавинообразного характера сигнала в биологической нейронной сети, что, по сути, сейчас моделирует искусственная нейронная сеть, наступает состояние эпилепсии.

Таким образом, задача в обработке данных именно лавинообразных сигналов приводит к искусственному интеллекту на новых физических принципах. Другими словами, обучение должно строиться не на исходных данных, а исключительно лишь на уникальной способности исходных данных к взаимной корреляции.

Лавины или процессы самоорганизованной критичности (СОК) характеризуются масштабной инвариантностью и достижением критичности без управляющего параметра. Масштабная инвариантность процессов СОК (лавина, землетрясение, детонация) делает их интуитивно непонятными в связи с тем, что в повседневной жизни чаще встречаемся с примерами, где важна размерность (масса, длина), когда размеры имеют значение. Модель песчаной кучи даёт наглядное представление систем СОК. Лавины отличаются между собой только некой безразмерной топологической характеристикой.

В статьях  предложен ряд нестандартных идей к описанию СОК: представление лавины в обычном пространстве подменяется представлением линейной системы во фрактальном пространстве (фрактальном многообразии). При этом возникает топологическая характеристика лавины, не имеющая аналога в пространствах целой размерности, — показатель связанности . Новая характеристика является платой за масштабную инвариантность процессов самоорганизованной критичности.

В работе  предложен способ построения фрактального многообразия в одномерном пространстве. Для ключевой характеристики лавины — показателя связанности  получена следующая формула:

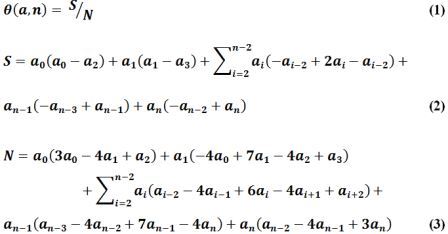
Топологическая характеристика — показатель связанности  определяется для произвольного набора данных. Квадратичные формы S и N всегда положительные. Метод неприменим для линейных данных и случайных чисел.

В обработке данных от сильно зашумлённых сигналов, а здесь видится эффективное применение, необходимо увеличивать точность. По опыту одной из успешно решённых задач, желательно иметь общее количество точек больше 2-3 тысяч, а показатель связанности рассчитывается в диапазоне от 100 до 500 точек с небольшим шагом в пять точек от начала данных до конца. Вычисляется суммарный показатель связанности и находится максимальное значение для некоторого диапазона. Значит, в найденном диапазоне исходных данных наиболее сильная связанность. Метод позволяет количественно сравнивать наборы данных между собой. Уточнение алгоритма и приведение других, более громоздких формул, значительно усложнит настоящее сообщение. Заметим, что формула (1) инвариантна относительно любых линейных преобразований исходных данных.

Уникальность формул (1 – 3) состоит в инвариантности показателя связанности  для множества точек функций Гаусса и Бесселя от гранулярности по n, для достаточно больших n. По-видимому, обнаружено новое свойство для известных функций Гаусса и Бесселя.

Пока накоплена небольшая практика в вычислениях показателя связанности. В каждой задаче существует своя специфика, понятная лишь владельцу задачи. Например, был бы интересен сравнительный анализ показателя связанности данных на фондовом рынке. Для этого необходимы оцифрованные данные биржевой кривой, которые непонятно где брать. Фондовый рынок представляет огромный научный интерес, выраженный в многочисленных публикациях посвящённых математическим оценкам коллективного бессознательного или стадного эффекта (оленеводство) .

Применение данного явно затратного метода может быть оправдано в случае ожидаемой самоорганизованной критичности данных, явной нелинейности данных, когда необходимо количественное сравнение коллективных эффектов. Например, прогноз землетрясений. Или в задачах локации, когда результат может быть важнее затрат. Существенным ограничением предложенного алгоритма является обработка данных только одномерного массива. В отдельных случаях возникала возможность из симметрии системы выделить одну размерность для решения задачи.

1.  Meisel, C., Storch, A., Hallmeyer-Elgner, S., Bullmore, E. & Gross, T. (2012) Failure of adaptive self-organized criticality during epileptic seizure attacks. PLOS Computational Biology 8, 1–8.

2. Milovanov, A.V. (1997) Topological proof for the Alexander-Orbach conjecture. Phys. Rev. E,   56, 2437-2446.

3. Зелёный Л.М., Милованов А.В., Фрактальная топология и странная кинетика: от теории перколяции к проблемам космической электродинамики, Успехи физических наук — 2004, №8, 809 – 852.

4. Владимиров В.В., Владимирова Е.В. Экономические аспекты развития технологий искусственного интеллекта // Экономика: вчера, сегодня, завтра. 2021. Том 11. № 6А. С.227-239.

5. Botsvadze I. Herd behavior in equity markets-the international evidence // Journal of Business. 2013. Vol. 2. N. 2. P. 41-46.

Виталий Владимиров vital.vladimirov@mail.ru