Реализуем алгоритм поиска в глубину

В этом туториале описан алгоритм поиска в глубину (depth first search, DFS) с псевдокодом и примерами. Кроме того, расписаны способы реализации поиска в глубину в C, Java, Python и C++.

“Поиск в глубину” или “обход в глубину” — это рекурсивный алгоритм по поиску всех вершин графа или дерева. Обход подразумевает под собой посещение всех вершин графа.

Алгоритм поиска в глубину

Стандартная реализация поиска в глубину помещает каждую вершину (узел, node) графа в одну из двух категорий:

1. Пройденные (Visited).

2. Не пройденные (Not Visited).

Цель алгоритма состоит в том, чтобы пометить каждую вершину как “Пройденная”, избегая при этом циклов.

Алгоритм поиска в глубину работает следующим образом:

1. Начните с того, что поместите любую вершину графа на вершину стека.

2. Возьмите верхний элемент стека и добавьте его в список “Пройденных”.

3. Создайте список смежных вершин для этой вершины. Добавьте те вершины, которых нет в списке “Пройденных”, в верх стека.

4. Необходимо повторять шаги 2 и 3, пока стек не станет пустым.

Пример реализации поиска в глубину

Предлагаю рассмотреть на примере, как работает алгоритм поиска в глубину. Мы будем использовать неориентированный граф с пятью вершинами.

Начнем мы с вершины “0”. В первую очередь алгоритм поиска в глубину поместит ее саму в список “Пройденные” (на изображении “Visited”), а ее смежные вершины — в стек.

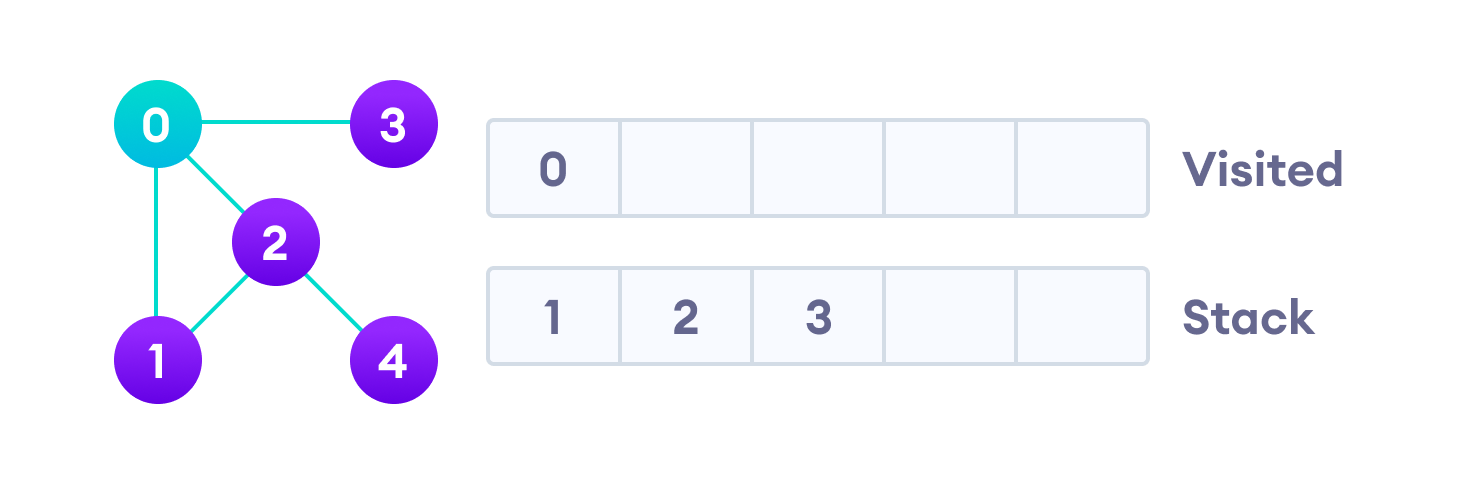
Затем мы берем следующий элемент сверху стека, т.е. к вершину “1”, и переходим к ее соседним вершинам. Поскольку вершина “0” уже пройдена, следующая вершина “2”.

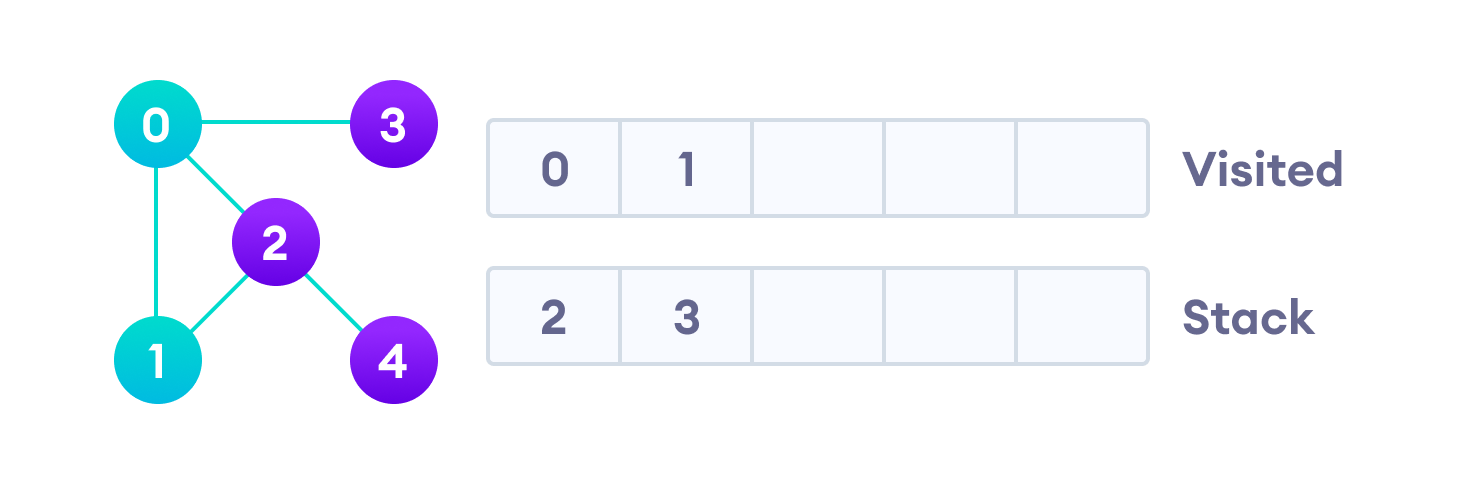
Вершина “2” смежна непройденной вершине “4”, следовательно мы добавляем ее наверх стека и проходим ее.

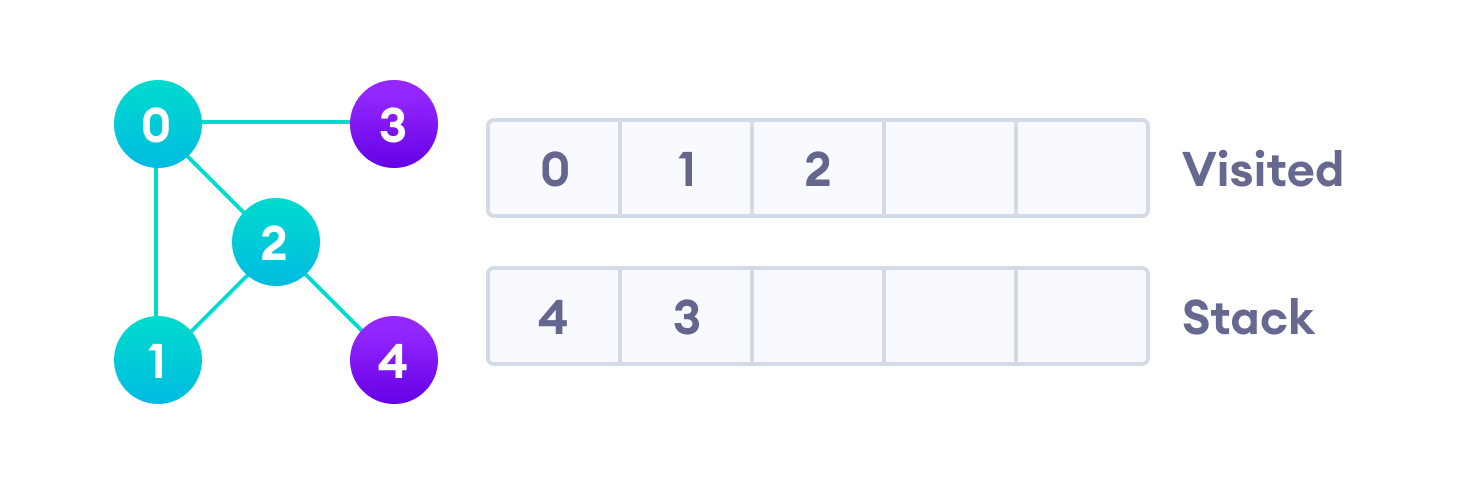
После того, как мы пройдем последний элемент (вершину “3”), в стеке не останется непройденных смежных вершин, и таким образом мы завершили обход графа в глубину.

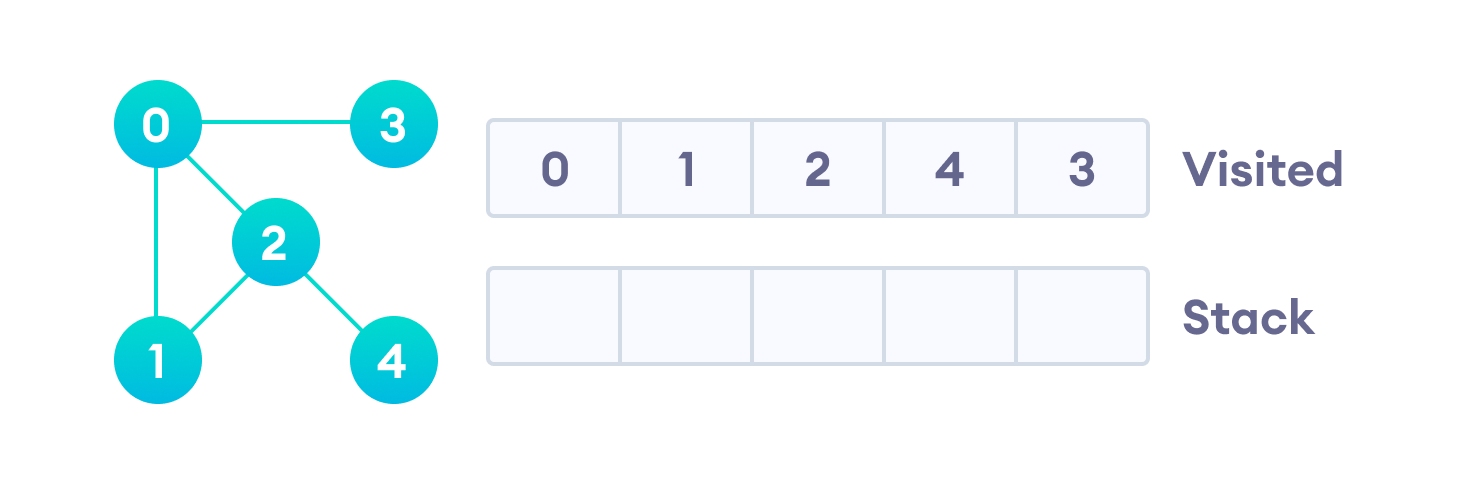
Псевдокод поиска в глубину (рекурсивная реализация)

Ниже представлен псевдокод для алгоритма поиска в глубину. Обратите внимание, что в функции init() необходимо запускать функцию DFS на каждой вершине. Это связано с тем, что граф может иметь две разные несвязанные части, поэтому для того, чтобы убедиться, что мы покрываем каждую вершину, мы должны запускать алгоритм поиска в глубину на каждой вершине.

DFS(G, u)     u.visited = true     for each v ∈ G.Adj[u]         if v.visited == false             DFS(G,v)       init() {     For each u ∈ G         u.visited = false      For each u ∈ G        DFS(G, u) }

Реализация поиска в глубину на Python, Java и C/C++

Ниже приведены примеры реально кода алгоритма поиска в глубину. Код был упрощен, чтобы мы могли сфокусироваться на самом алгоритме, а не на других деталях.

# Алгоритм поиска в глубину на Python   # Алгоритм def dfs(graph, start, visited=None):     if visited is None:         visited = set()     visited.add(start)      print(start)      for next in graph[start] - visited:         dfs(graph, next, visited)     return visited   graph = {'0': set(['1', '2']),          '1': set(['0', '3', '4']),          '2': set(['0']),          '3': set(['1']),          '4': set(['2', '3'])}  dfs(graph, '0')

// Алгоритм поиска в глубину на Java import java.util.*;   class Graph {   private LinkedList<Integer> adjLists[];   private boolean visited[];     // Создание графа   Graph(int vertices) {     adjLists = new LinkedList[vertices];     visited = new boolean[vertices];       for (int i = 0; i < vertices; i++)       adjLists[i] = new LinkedList<Integer>();   }     // Добавление ребер   void addEdge(int src, int dest) {     adjLists[src].add(dest);   }     // Алгоритм    void DFS(int vertex) {     visited[vertex] = true;     System.out.print(vertex + " ");       Iterator<Integer> ite = adjLists[vertex].listIterator();     while (ite.hasNext()) {       int adj = ite.next();       if (!visited[adj])         DFS(adj);     }   }     public static void main(String args[]) {     Graph g = new Graph(4);       g.addEdge(0, 1);     g.addEdge(0, 2);     g.addEdge(1, 2);     g.addEdge(2, 3);       System.out.println("Following is Depth First Traversal");       g.DFS(2);   } } 

// Алгоритм поиска в глубину на C   #include <stdio.h> #include <stdlib.h>   struct node {   int vertex;   struct node* next; };   struct node* createNode(int v);   struct Graph {   int numVertices;   int* visited;     // Нам нужен int** для хранения двумерного массива.   // Аналогично, нам нужна структура node** для хранения массива связанных списков.   struct node** adjLists; };   // Алгоритм void DFS(struct Graph* graph, int vertex) {   struct node* adjList = graph->adjLists[vertex];   struct node* temp = adjList;     graph->visited[vertex] = 1;   printf("Visited %d \n", vertex);     while (temp != NULL) {     int connectedVertex = temp->vertex;       if (graph->visited[connectedVertex] == 0) {       DFS(graph, connectedVertex);     }     temp = temp->next;   } }   // Создание вершины struct node* createNode(int v) {   struct node* newNode = malloc(sizeof(struct node));   newNode->vertex = v;   newNode->next = NULL;   return newNode; }   // Создание графа struct Graph* createGraph(int vertices) {   struct Graph* graph = malloc(sizeof(struct Graph));   graph->numVertices = vertices;     graph->adjLists = malloc(vertices * sizeof(struct node*));     graph->visited = malloc(vertices * sizeof(int));     int i;   for (i = 0; i < vertices; i++) {     graph->adjLists[i] = NULL;     graph->visited[i] = 0;   }   return graph; }   // Добавление ребра void addEdge(struct Graph* graph, int src, int dest) {   // Проводим ребро от начальной вершины ребра графа к конечной вершине ребра графа   struct node* newNode = createNode(dest);   newNode->next = graph->adjLists[src];   graph->adjLists[src] = newNode;     // Проводим ребро из конечной вершины ребра графа в начальную вершину ребра графа   newNode = createNode(src);   newNode->next = graph->adjLists[dest];   graph->adjLists[dest] = newNode; }   // Выводим граф void printGraph(struct Graph* graph) {   int v;   for (v = 0; v < graph->numVertices; v++) {     struct node* temp = graph->adjLists[v];     printf("\n Adjacency list of vertex %d\n ", v);     while (temp) {       printf("%d -> ", temp->vertex);       temp = temp->next;     }     printf("\n");   } }   int main() {   struct Graph* graph = createGraph(4);   addEdge(graph, 0, 1);   addEdge(graph, 0, 2);   addEdge(graph, 1, 2);   addEdge(graph, 2, 3);     printGraph(graph);     DFS(graph, 2);     return 0; } 

// Алгоритм прохода в глубину в C++   #include <iostream> #include <list> using namespace std;   class Graph {   int numVertices;   list<int> *adjLists;   bool *visited;      public:   Graph(int V);   void addEdge(int src, int dest);   void DFS(int vertex); };   // Инициализация графа Graph::Graph(int vertices) {   numVertices = vertices;   adjLists = new list<int>[vertices];   visited = new bool[vertices]; }   // Добавление ребер void Graph::addEdge(int src, int dest) {   adjLists[src].push_front(dest); }   // Алгоритм  void Graph::DFS(int vertex) {   visited[vertex] = true;   list<int> adjList = adjLists[vertex];     cout << vertex << " ";     list<int>::iterator i;   for (i = adjList.begin(); i != adjList.end(); ++i)     if (!visited[*i])       DFS(*i); }   int main() {   Graph g(4);   g.addEdge(0, 1);   g.addEdge(0, 2);   g.addEdge(1, 2);   g.addEdge(2, 3);     g.DFS(2);     return 0; }

Сложность алгоритма поиска в глубину

Временная сложность алгоритма поиска в глубину представлена ​​в виде O(V + E), где V — количество вершин, а E — количество ребер.

Пространственная сложность алгоритма равна O(V).

Применения алгоритма

1. Для поиска пути.

2. Для проверки двудольности графа.

3. Для поиска сильно связанных компонентов графа.

4. Для обнаружения циклов в графе.

Приглашаем всех желающих на открытый урок в OTUS «Теория графов. Термины и определения. Основные алгоритмы», регистрация доступна по ссылке.