Дифференциальный криптоанализ алгоритма DES

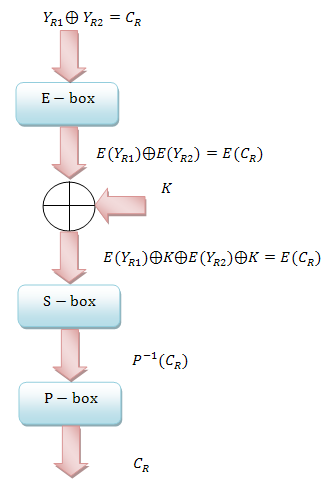
Итак, как уже говорилось в предыдущей главе, идея ДК заключается в последовательном сравнении пар открытый/закрытый текст в результате их прохождения через алгоритмы шифрования. Учитывая, что вся информация представляется в двоичном виде, под разностью подразумевается сумма двух последовательностей по модулю два (побитовый XOR). В самом начале анализа алгоритма принято отбрасывать начальную и конечную перестановки (P- блоки), так как они линейны. Рассмотрим один раунд шифрования DES:

Рисунок 1 – Дифференциальный криптоанализ одного раунда шифрования DES

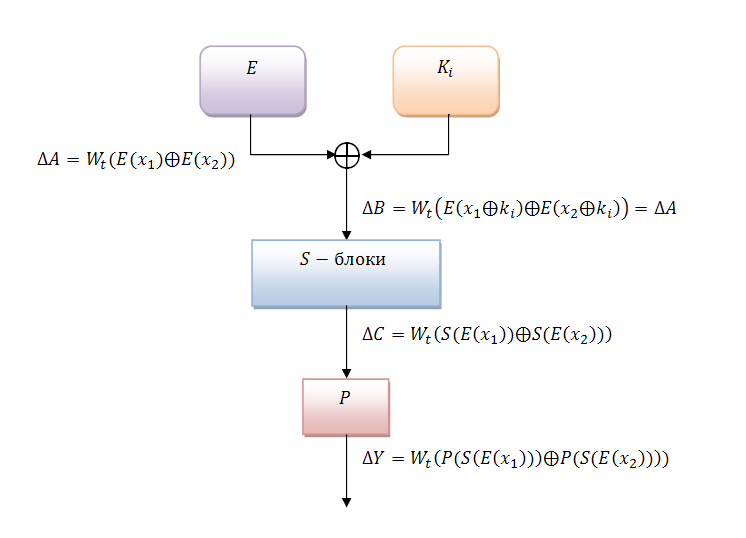
Введем следующие обозначения. Пусть нам будет задана входная пара и , имеющие разность $\Delta X$ , а так же пара выходов и с разностью $\Delta Y$ . Так как расширяющая перестановка с блоком известны, мы можем посчитать разность на выходе после нее и записать как $\Delta A$ . Эта разность после прохождения через S даст $\Delta C$ , которая после перестановки даст $\Delta Y$ . Остаётся вопрос о подключе. После выхода из сумматора XOR разность $\Delta B$ будет равна $\Delta A$ , потому что подключ будет складываться с самим собой. Иными словами:

$E(x_1 \bigoplus k_i)\bigoplus E(x_2 \bigoplus k_i) = E(x_1)\bigoplus E(x_2)$

Таким образом, подключ не влияет на конечную разность. Можно доказать, что соответствия между $\Delta A$ и $\Delta C$ носят не равновероятный характер в силу особенностей строения S — блоков. Знать соответствие между этими двумя значениями крайне важно, так как благодаря этому можно восстановить раундовый подключ. Как уже говорилось выше, длина раундового подключа равна 48 бит, однако, зная алгоритм развёртки ключа, можно восстановить целый 56 – битный ключ методом полного перебора, используя всего $2^{8}$ комбинаций. Метод ДК позволяет вскрывать подключ $K_{16}$ . Так как наблюдается несходство различных пар $\Delta A$ и $\Delta C$ , вероятность появления того или иного шифртекста также не равновероятная. В следующем пункте мы сформулируем алгоритм нахождения статистики и построим таблицы для каждого S — блока замены.

Если при определенном количестве пар у нас выявляется наибольшее количество совпадений, то в этом случае подключ подобран верно. В таком случае дана пара, которая соответствует разностям $\Delta A$ и $\Delta C$ , называется правильной парой. Для того, чтобы отыскать нужный подключ, необходимо собрать как можно большее количество правильных пар. Далее, правильный подключ будет появляться чаще остальных.

Рисунок 2 – Однораундовая характеристика DES

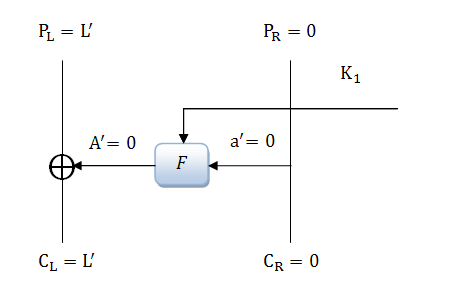
Именно в этих операциях и заключается метод ДК. В одной из работ А. Шамира показано как, зная характеристику одного раунда шифрования, построить характеристику для нескольких раундов. На рисунке 2.7 изображена характеристика одного раунда шифрования. Входное значение разбито на две части и , причем, правая часть равна нулю. Это сделано с той целью, чтобы на выходе функции было нулевое значение. Это означает, что на выходе мы всегда получим эту же разность.

Если привести пример ненулевой входной разности, то он представлен на рисунке 3

Рисунок 3 – Однораундовая характеристика DES с ненулевой разностью

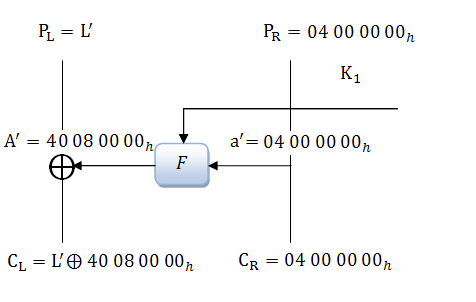
Здесь в качестве входной разности берется значение $L^{'}.$ , где символ означает конкатенацию строк. Она подобрана таким образом, чтобы на выходе из раундовой функции было значение . Соответственно, полученный шифртекст будет иметь значение $L^{'}\bigoplus 40080000_h . 04000000_h$ . Причины подбора тех или иных цифр самим Шамиром не были объяснены.

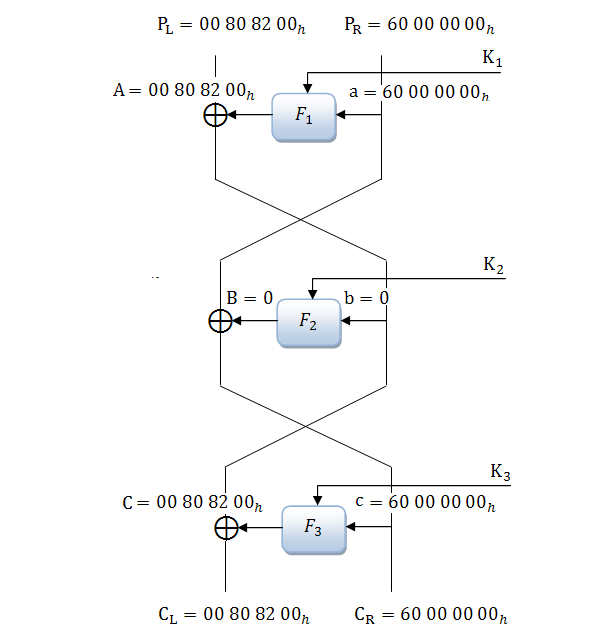
Далее рассмотрим пример с несколькими раундами. На рисунке 2.9 приведена схема алгоритма DES с тремя раундами.

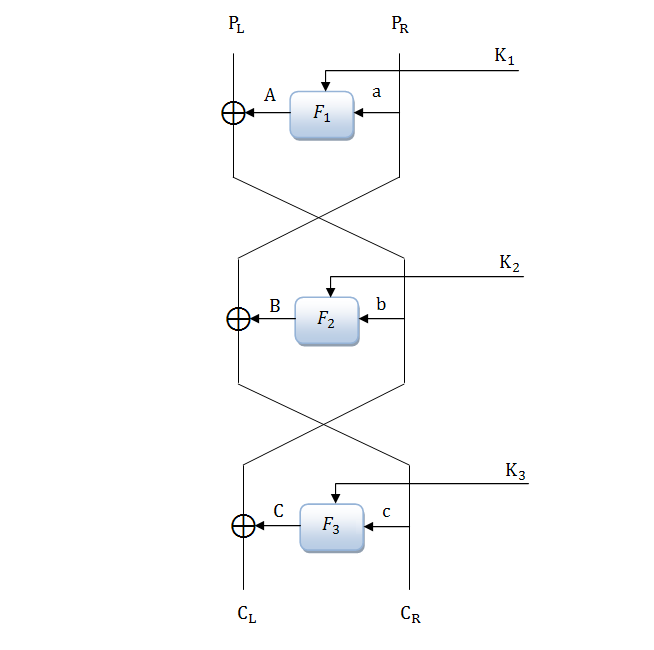
Будем исходить из того, что правая часть входной разности нулевая, так же как и в однораундовой характеристике. Это соответствует a=0 на рисунке 2. В таком случае Разность A также всегда будет нулевой, и на вход функции F второго раунда поступит разность . На выходе мы будем иметь шифртекст $P_L\bigoplus C.F_2(P_L)$ . По значениям и нетрудно определить биты подключа последнего раунда, а после чего восстановить весь ключ.

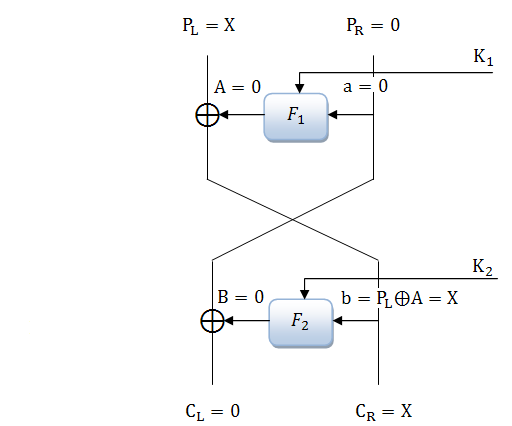
Помимо этого существует еще один способ, позволяющий анализировать алгоритм. Мы можем подобрать такую входную разность (а именно, значение правой части), что на выходе из функции F мы получим значение из левой части. Из этого следует, что на вход второго раунда поступит нулевая разность, которая в свою очередь при прохождении через раундовую функцию даст значение, равное правой половине исходного текста . На рисунке 5 отображена подобная характеристика.

Рисунок 5 – Трехраундовая характеристика алгоритма DES

Для того, чтобы провести атаку на полный 16 – раундовый DES Шамир предложил использовать двухраундовую характеристику и использовать такой дифференциал, который при прохождении через функцию F давал нулевую разность. Подобная структура отображена на рисунке 6. В качестве примера можем рассмотреть случай, когда входная разность равна . Что же будет происходить в функции F? В таком случае в каждом нечетном раунде на её вход будет поступать нулевая разность, что на выходе также даст нулевой результат. В каждом же четном раунде в раундовую функцию будет поступать результат сложения прежней левой части и выходной нулевой разности в нечетном раунде. В данном случае это . На вход первых трех S – блоков поступит , и . соответственно. На остальные S – блоки поступят нули. На выходе от разности , что равно мы получим нули с вероятностью . Вероятность того, что на выходе второго S – блока будет нулевая разность составляет , а вероятность того, что на выходе третьего S – блока будет нулевая разность составляет .

Рисунок 6 – Двухраундовая характеристика алгоритма DES

Нетрудно посчитать, что суммарная вероятность получения нулевой разности по трем S – блокам составляет: $P=(14/64)*(8/64)*(10/64)=1/2^{7.87}$

Для анализа 16 – раундового DES было предложено использовать подобную характеристику 6 раз, — со 2- го по 13-ый раунды. В таком случае на вход 14- го раунда поступит нулевая разность. Так как нам известна выходная разность 14-го и 16-го раунда, мы можем определить разность 15-г раунда. Благодаря статистическим данным нам может стать известна разность после прохождения через F – функцию 16-го раунда. Последние три раунда всегда будут выполняться со стопроцентной вероятностью. Вероятность же выполнения шести двухраундовых характеристик равна:

$p=(1/2^{7.87})^{6}=1/2^{47.22}$

Следующий рисунок наглядно демонстрирует применение анализа к полному алгоритму DES

Рисунок 7 –Характеристика полного алгоритма DES

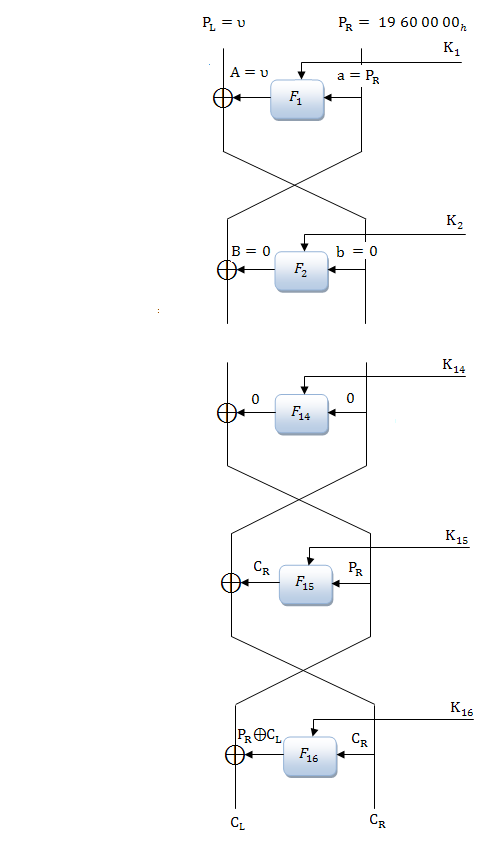
Учитывая, что правая часть входной разности равна , то всего существует $2^{12}$ возможных вариантов для её получения. Левая входная разность может принимать практически любые значения.

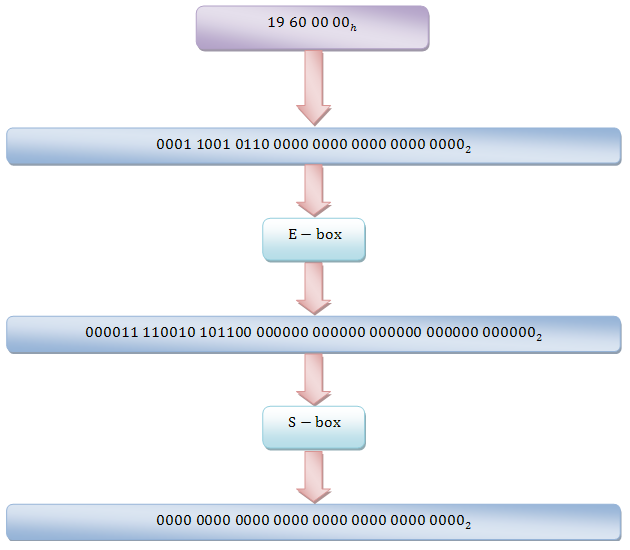
Для того чтобы начать искать подключ, необходимо собрать статистические данные о криптографических примитивах, входящих в исследуемый алгоритм шифрования. В данном случае, это будут S – блоки. Именно от них зависит стойкость шифра и степень лавинного эффекта на каждом раунде. В DES каждый S – блок принимает на вход 6 битов, а на выходе выдает 4. Ввиду подобной несбалансированности длина подключа изначально не соответствует размеру блока данных, с которым будет складываться. Для того, чтобы это обеспечить, используют E – блок, который расширяет подключ до 48 бит (по 6 бит на каждый из 8-ми S – блоков).

Итак, имеется необходимость построить таблицы соответствия входной и выходной разностей, – $\Delta A$ и $\Delta C$ соответственно. Каждая разность $\Delta A$ может иметь 64 различных значений. К примеру, при $\Delta A=111010_2$ это может быть сумма и или же и и так далее. Теперь, если мы каждое из этих значений подвергнем преобразованию через первый S – блок, то увидим, что значению соответствует , значению , — . Это означает, что разности $\Delta A=111010_2$ в одном из случаев соответствует $\Delta C=0010_2 \bigoplus 0101_2=0111_2$ .

Теперь можно сформулировать алгоритм анализа S – блоков, который можно будет применить не только к DES, но и к любому другому алгоритму шифрования:

Возьмем дифференциал . Подберем два таких открытых текста, для которых $x_1 \bigoplus x_2=X$
Каждое значение прогоняем через анализируемый S–блок.
Затем складываем между собой получившиеся значения.
Далее подбираем другое значение и , которые так же в сумме дают исходный дифференциал и возвращаемся к пунктам 2 и 3.
Так продолжаем раз, где – разрядность входа S–блока.
После подсчитываем число похожих выходных разностей.
Берём следующий дифференциал и так раз.

Таблица 1 – Пример статистических данных для первого S–блока алгоритма DES

На основе полученных таблиц мы можем сделать следующие выводы. Во-первых, сумма всевозможных значений разности $\Delta C$ всегда равна 64. Для того, чтобы посчитать вероятность появления того или иного значения при заданных $\Delta A$ и $\Delta C$ необходимо поделить частоту появления на 64. Из таблиц видно, что максимально возможная вероятность появления $\Delta C$ равна 1/4. Также стоит обратить внимание на то, что все значения четные. Это объясняется тем, что каждому дифференциалу соответствует по две пары $x_1 \bigoplus x_2$ и $x_2 \bigoplus x_1$ .

Перво-наперво, определяем на какие S – блоки какие значения отправятся. Для этого заданный дифференциал подвергается E – преобразованию. После этого становится очевидно, что только на вход второго S – блока поступит ненулевое значение, в то время как на остальные поступят нули. Далее, на основе полученных таблиц мы определяем, что дифференциалу $\Delta A =001000_2$ с наибольшей вероятностью соответствует разность . После этого полученный результат проходит через P – преобразование, что в итоге дает . Если в изначальной входной разности левая часть будет равна этому значению, то на вход второго раунда поступит нулевая разность.

Теперь рассмотрим другую разность, которая представлена на рисунке 5. Здесь точно также, после E – преобразования на все S – блоки, кроме первого, поступят нули. На вход первого S – блока поступит дифференциал $\Delta A=001100_2$ , которому соответствует разность (с вероятностью 14/64). После P – преобразования полученная разность будет равна .

Рисунок 8 – Преобразование входной разности в функции F

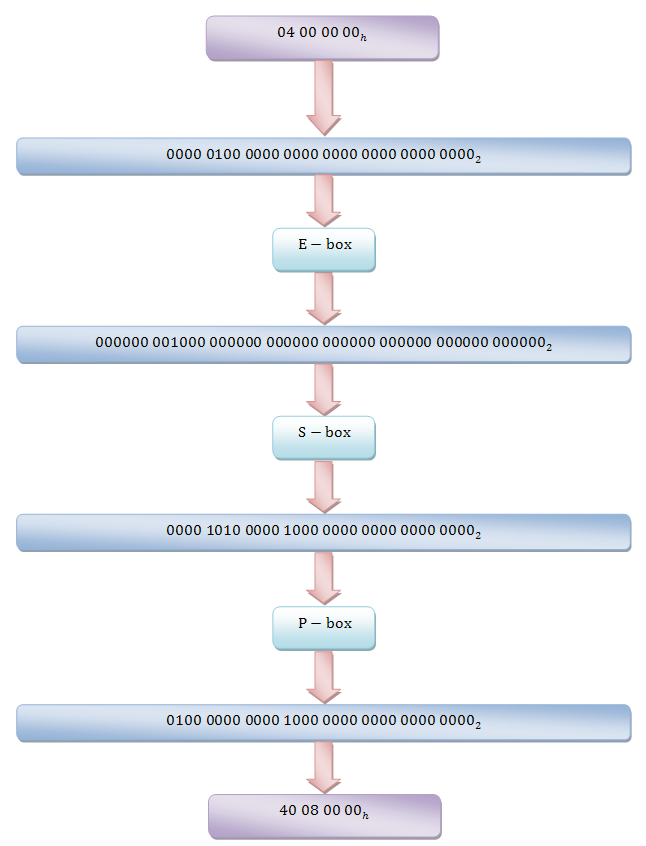
В работах Шамира было предложено использовать на самую наиболее вероятную пару по той причине, что в таком случае пришлось бы затрагивать большое количество S – блоков ввиду E – преобразования. Выбранный дифференциал является наиболее компромиссным вариантом, так как затрагивает лишь три блока замены. Нетрудно посчитать, что для этого будет использоваться лишь $2^{12}$ возможных значений. E – преобразование повторяет крайние биты для каждого из блоков замены, в связи с чем есть необходимость, чтобы два первых и два последних бита всегда были равны нулю. Таких комбинаций всего четыре: , , и . Первая среди них всегда дает нулевое значение, а три остальные никогда не дают его ни для одного блока замены. Выше было установлено, что суммарная вероятность получения нулевой разности по трем S – блокам составляет: $P=(14/64)*(8/64)*(10/64) =1/2^{7.87}$

Если мы переберем всевозможные значения, которые могут дать нулевую разность с вероятностью большей заданной, то получим и . Поэтому, для анализа можно использовать эти два дифференциала. На основе этого алгоритма можно осуществить поиск правильных пар, а затем и искомого секретного ключа. Итак, на рисунке 7 представлена схема анализа алгоритма DES для всех 16-ти раундов. Здесь явно определена правая часть, равная , в то время как левая может принимать практически любые значения. Итак, на вход первого блока поступает разность . По составленным таблицам определяем, что при этом значении на выходе никогда не получится разность и . Аналогично, для второго блока замены при значении никогда не выйдет разность , а для третьего блока, — .

Рисунок 9 – Преобразование входной разности 19600000h в функции F

Так как в правой части значащими битами являются лишь первые 12, то всего может быть $2^{12}$ вариантов. Из них невозможными являются следующие значения: , , и . Нетрудно посчитать, что число невозможных дифференциалов составляет . За счет этого мы можем сократить время вычисления на (1024/4096)*100%=25%.

Конечная разность, получающаяся на выходе из раундовой функции, является результатом P – преобразования. В таблице 2 показано, какие из этих битов соответствуют первым 12 битам входной разности. Именно эти биты и должны подвергаться изменению. При этом необходимо помнить, что в левой части могут встречаться не все комбинации. Как уже отмечалось ранее, атака на полный алгоритм DES полностью строится на анализе двух последних раундов. На выходе мы имеем разность и . Правая часть разности должна получиться в результате прохождения через функцию F. Как мы уже определили, эта разность может быть получена 3072 различными способами. Если же мы получим любую другую разность, — это будет означать, что выбрана пара заведомо не правильная.

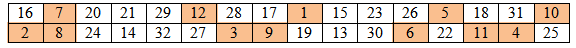
Таблица 2 - P – преобразование в функции F — Таблица 2 — P – преобразование в функции F

После того, как мы определили, что имеет допустимое значение, можно приступить к рассмотрению . Для начала прибавим к ней разность , чтобы получить то значение, которое получается на выходе из раундовой функции F.

Рисунок 10 – Преобразование входной разности 19600000h в функции F

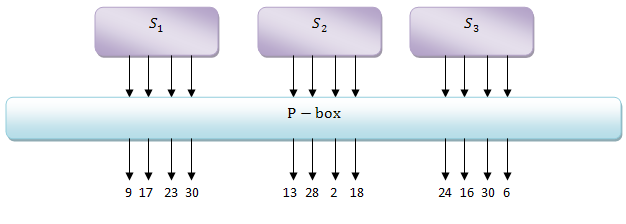
На рисунке 10 изображены те биты, на которые накладываются ограничения в виду невозможных дифференциалов. Итак, сформулируем алгоритм поиска правильных пар:

Для начала побираются правые части открытого текста $X_{R1}$ и $X_{R2}$ таким образом, чтобы $X_{R1} \bigoplus X_{R2}=19600000_h$ .
Подбирается левая часть , на которую накладываются следующие ограничения:

a. 9, 23 и 31 одновременно не равны единице;

b. 2, 13, 18 и 28 биты одновременно не равны единице;

c. 6, 24 и 30 биты одновременно не равны нулю, а 16 бит – единице;

Подбираются два значения $X_{L1}$ и $X_{L2}$ таким образом, чтобы $X_{L1}\bigoplus X_{L2}=P_L$ .
Далее, выбранные пары $X_{L1}X_{R1}$ и $X_{L2}X_{R2}$ подвергаются шифрованию, после чего на выходе получаются пары $Y_{L1}Y_{R1}$ и $Y_{L2}Y_{R2}$ .
Теперь определяется правая часть $C_R=Y_{R1}\bigoplus Y_{R2}$ Если она удовлетворяет критериям пункта 2, то приступаем к следующему шагу. В противном случае подбирается новая пара $X_{L1}X_{R1}$ и $X_{L2}X_{R2}$
Определяется левая часть $C_{L}= Y_{L1}\bigoplus Y_{L2}$ . Если $C_L\bigoplus196000_h$ удовлетворяет критериям пункта 2, то приступаем к следующему шагу. В противном случае подбирается новая пара $X_{L1}X_{R1}$ и $X_{L2}X_{R2}$
Далее все пункты повторяются для всех возможных значений $X_{L1}$ и $X_{R1}$ .

Так как вероятность нахождения ключа для полного алгоритма DES составляет $2^{-47.22}$ то по нижеприведенной мы можем определить минимальное число текстов, проанализировав которые можно с вероятностью 0.5 найти верный ключ: $k=\sqrt{2*2^{64}ln2^{-47.22}}=2^{35}$ .

Как уже говорилось ранее, со второго по 15 раунд мы используем двухраундовую характеристику, что позволяет использовать разработанный алгоритм для анализа меньшего количества раундов.

Теперь, когда мы нашли правильные пары текстов, можно приступить к поиску секретного ключа.

Рисунок 11 – Последний раунд шифрования DES

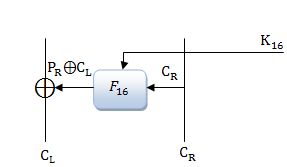
На рисунке 11 изображен последний раунд шифрования. Очевидно, что мы можем определить входное значение в функцию F, зная . Также, мы можем найти значение выхода из этой функции, посчитав $C_L\bigoplus 19600000_h$ . Применив E – преобразование к входной разности и обратное P – преобразование к выходной, мы можем найти соответствие между ними. На основе этого сформулируем алгоритм подбора секретного ключа:

Определение разности на выходе из F-функции, сложив $C_L\bigoplus19600000_h$
Применить обратное P — преобразование $C_L\bigoplus19600000_h$ к этой разности.
Применить E – преобразование к разностям $Y_{R1}$ и $Y_{R2}$
Сложить полученные значения $E(Y_{R1})$ и $E(Y_{R2})$ с произвольным ключом $K_{ij}$ и подвергнуть S – преобразованию.
Если значения $S(Y_{R1})\bigoplus S(Y_{R2})$ равны $P _{inv}(C_R)$ , то счетчик ключа $K_{ij}$ необходимо увеличить на единицу.
Ключи, имеющие максимальное значение счетчиков, и будут наиболее вероятными.

Рисунок 12 – Функция F последнего раунда шифрования DES

Проанализировав таким образом все найденные правильные пары текстов, можно определить 48-битный подключ $K_{16}$ после чего восстановить остальные 8 бит методом полного перебора. В таблице 7 показано соответствие между битами основного ключа и 16-го.

Таблица 3 – Соответствие битов основного ключа и подключа 16 раунда

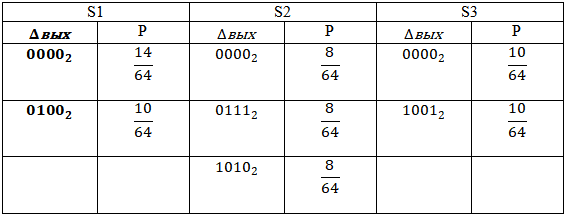
В предыдущих пунктах было определено, что левая часть входной разности может принимать одно из 3072 значений. Согласно построенной статистике, не все эти значения могут быть равновероятны. Если проанализировать имеющиеся данные в таблицах, то мы увидим, что существует всего 7 значений, вероятность появления которых выше 1/8. Для первого блока это и , для второго, — , и , а для третьего, — и . Нетрудно посчитать, что всего существует 12 различных комбинаций этих значений. При их анализе также необходимо учитывать, что после S – преобразования следует перестановка P.

Таблица 4 - Наиболее вероятные значения выходных разностей для первых трех S – блоков DES — Таблица 4 — Наиболее вероятные значения выходных разностей для первых трех S – блоков DES

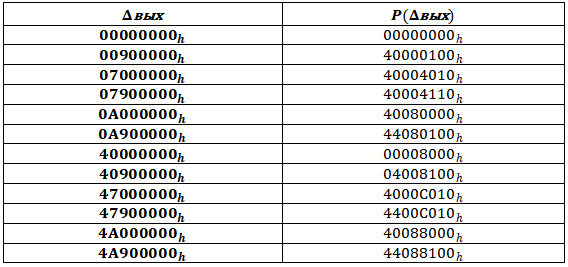
Если проанализировать все 12 комбинаций этих значений, то получим разности, представленные в таблице 9. Именно среди этих разностей есть большая вероятность нахождения правильных пар.

Таблица 5 – Наиболее вероятные дифференциалы

Используемая литература:

Шнайер Б. Прикладная криптография: Протоколы, алгоритмы, исходные тексты на языке СИ. – М.:ТРИУМФ. – 2002
Heys H. M. A Tutorial on Linear and Differential Cryptanalysis [Электронный ресурс]. http://www.engr.mun.ca/~howard/PAPERS/ldc_tutorial.pdf
D. Coppersmith The Data Encryption Standard (DES) and its strength against attacks VOL. 38 NO. 3 MAY 1994
Бабенко Л. К., Ищукова Е. В. Особенности применения методов дифференциального криптоанализа к симметричным блочным шифрам Вопросы кибербезопасности №1(9) — 2015
Сивцев Д. А. Подбор ключей симметричного алгоритма шифрования DES методом дифференциального криптоанализа. Тенденции инновационных процессов в науке: сборник статей Международной научно – практической конференции – Москва: РИО ЕФИР, 2015. стр. 29
E. Biham, A. Shamir. Differencial Cryptoanalysis of DES-like Cryptosystems. The Weizmann Institute of Science Departament of Apllied Mathematics, July 19, 1990 p. 13
E. Biham, A. Shamir. Differencial Cryptoanalysis of the Full 16-round DES p. 491
Ященко В. В. Введение в криптографию – СПб.: Питер, 2001 стр. 78

ссылка на оригинал статьи https://habr.com/ru/post/661205/

Дифференциальный криптоанализ алгоритма DES

Комментарии

Добавить комментарий Отменить ответ