«Ваша сезонность, сэр!»: ищем тренд и прогнозируем спрос с помощью временных рядов, SARIMA и Python. Ч.1

Как вы можете помнить по первой статье «Маркетинговая аналитика на Python. Пишем код для RFM-сегментации», более 8 лет я работаю в сфере маркетинга для B2B и примерно столько же бешусь от дилетантского подхода к аналитике, который тянет за собой ряд проблем с определением ключевых метрик эффективности для компании (и, как следствие, с мотивацией сотрудников):

• План продаж распределен «от балды», невыполним или выполним слишком легко. А доказать релевантность плана спросу сотрудникам без математического моделирования — невозможно.

• Вечный дефицит на складе …

• …Или «протухает» товар с ограниченным сроком годности

  Но, как говорил Паскаль, величие человека — в его способности мыслить, поэтому попробуем разобраться в этой и следующей статье, как спрогнозировать продажи по точной математической модели с учетом тренда и сезонности с помощью Python в Jupiter Notebook.

  Мы будем использовать понятие временного ряда. Звучит жутко, но если вы — интернет-маркетолог, то уже используете в работе временные ряды и даже, o mamma mia, сглаживаете их, когда переходите в статистике Яндекс.Метрики от сегментации по дням к сегментации по неделям и\или месяцам. Временной ряд — ни что иное, как значение параметра, записанного в разные моменты времени (или график функции y(t), где y может быть продажами, трафиком на сайт или в приложение и т.д.). В интернете вещей (IOT) временной ряд может использоваться для анализа работоспособности устройств.

  Значение временного ряда можно представить как уровень (level), тенденцию (trend), сезонность (seasonality) и шум (noise):

  • Уровень: Среднее значение (здесь речь идет о среднем арифметическом)

  • Тенденция: Показывает, значение склонно увеличиваться или уменьшаться

  • Сезонность: Повторяющийся краткосрочный цикл

  • Шум: Случайное изменение в ряду, не коррелирующее с другими данными

  Различают аддитивную и мультипликативную модели временных рядов. Мультипликативная модель временного ряда используется в случаях, когда амплитуда колебаний изменяется с течением времени. Мы будем использовать данные о продажах стоматологических имплантов за 3 года (аддитивный временной ряд), где y(t) = Level + Trend + Seasonality + Noise.

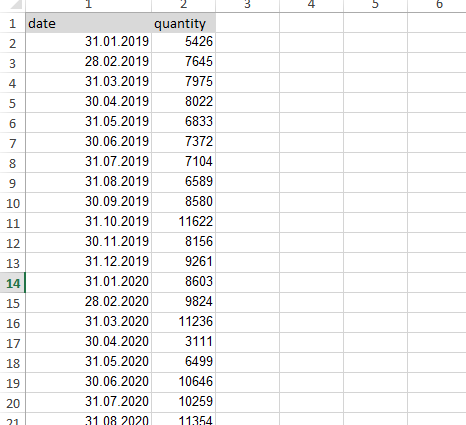
  1. Прежде всего выполним предобработку данных о продажах и сохраним ее в excel, данные о продажах за месяц соответствуют последнему дню месяца. :

  #обязательно отформатируйте в Excel всю колонку date как дату для корректного открытия в Jupiter Notebook

  

  2. Импортируем необходимые для работы библиотеки:

import numpy as np import pandas as pd from datetime import datetime import matplotlib.pyplot as plt

Преобразуем наш файл в датафрейм и любуемся на него (я часто так делаю, вызываю датафрейм, чтобы просто на него посмотреть — становится хорошо, спокойно и чуть больше красоты вокруг):

#сохраняем таблицу в датафрейм dentium_raw = pd.read_excel('C://Users//Света//Desktop//RFM Библиотеки Python ПК ППЗ//sarima_dentium_raw.xlsx')

Устанавливаем колонку с датой в качестве индекса и посмотрим на датафрейм с переназначенным индексом:

#устанавливаем колонку с датой в качестве индекса  dentium_raw=dentium_raw.set_index('date')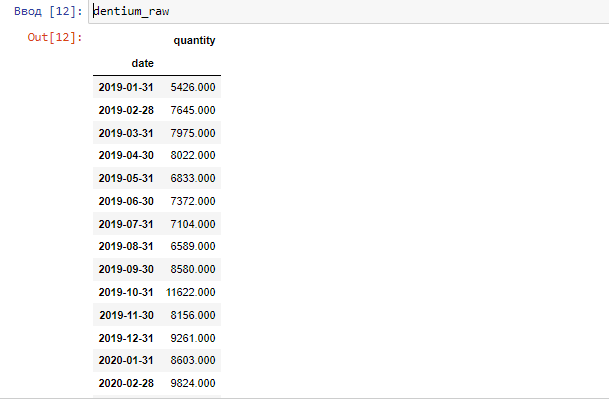

Построим график продаж на основании датфрейма:

dentium_raw.plot() plt.show()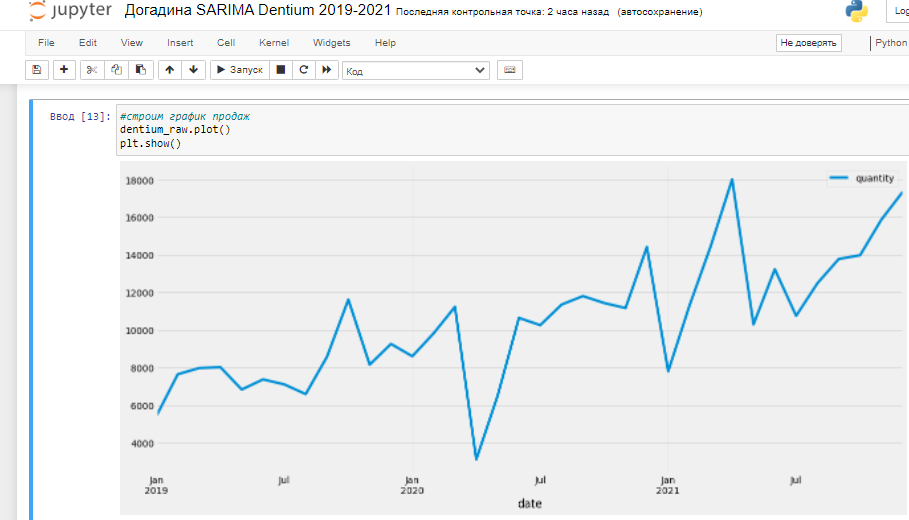

Какие выводы можно сделать? Наблюдается выброс в апреле 2020 — отгружено более, чем в 2 раза меньше позиций, чем даже в самый «низкий» месяц. Выброс связан с началом коронавирусного локдауна и требует обработки, заменим их на статистически более достоверные продажи. Средние продажи за месяц не подходят — наблюдается возрастающий тренд, есть подозрение на сезонность (проверим ее в конце). Лучше опираться на разницу значений с предыдущим месяцем в прошлом и будущем году — это будет учитывать и тренд, и сезонность спроса. Разница марта к апрелю 2019 — +0,6%, 2021 — +24,5%, среднее — 12,5%. Применим ее к апрелю 2020 по отношению к марту. Май 2020 также нужно будет скорректировать на среднее разницы значений 14,9% и 42,9% — 28,9%. Почистили датасет:

dentium_april_clean = pd.read_excel('C://Users//Света//Desktop//RFM Библиотеки Python ПК ППЗ//sarima_april_out.xlsx')

И теперь установим дату как индекс и построим график:

#установили дату как индекс dentium_april_clean = dentium_april_clean.set_index('date') dentium_april_clean.plot() plt.show()

Осталось произвести декомпозицию очищенного от выброса датасета. Мы помним, что значение временного ряда — y(t) = Level + Trend + Seasonality + Noise . значит, для того, чтобы найти сезонное значение, нужно из значения вычесть среднее, вычесть значения шума и тренда. Это мы и произведем с помощью библиотеки statsmodels : проведем декомпозицию временного ряда вполне коротким кодом. Здесь важно правильно назначить частоту freq, у нас в данных 3 цикла (3 года) по 12 месяцев, частота будет равняться 12:

#добавим нужную библиотеку import statsmodels.api as sm #произведем декомпозицию временного ряда  decomposition = seasonal_decompose(dentium_april_clean, freq=12) fig = decomposition.plot() plt.show()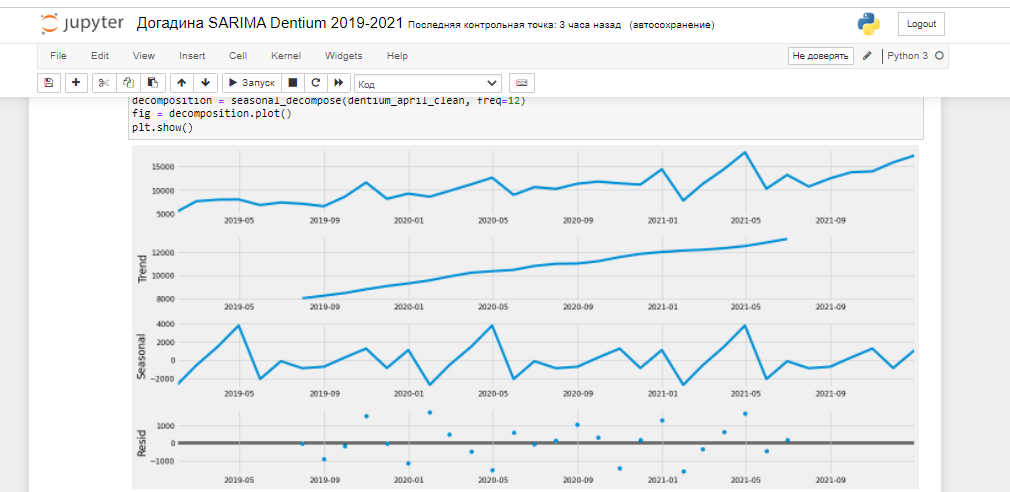

Восходящий тренд был очевиден, а вот майский всплеск спроса несколько нов. Гипотеза такова: летом имплантацию стараются не производить из-за сложного процесса приживления в жару, тем не менее, до сезона отпусков врачи стараются произвести имплантации и\или пополнить запасы склада клиники. Декабрьский спрос может быть связан, в том числе, с необходимость освоить бюджет клиники, ну а январь — классически месяц низкого спроса во многих нишах. Во второй части этой статьи мы построим прогноз продаж с помощью модели SARIMA.

Python доступен и полезен всем руководителям и маркетологам, и я надеюсь, что мои статьи и код в них помогут вам более точно производить маркетинговую, бизнес-аналитику, даже если у вас нет бюджета на сложные CRM-системы и содержание аналитика в штате.

Обняла 🙂