Модели для последовательностей != рекуррентные сети, или «все гениальное — просто»

Недавно нашел статью 2018 года, в которой авторы поставили себе целью продемонстрировать, что не стоит смотреть на задачи, входы/выходы в которых являют собой последовательности, исключительно сквозь призму рекуррентных сетей, а в результате не только добились своей цели, но еще и улучшили state-of-the-art на модификации небезызвестного MNIST, однако, как водится, обо всем по порядку.

О чем, собственно, речь?

Авторы статьи, как они сами утверждают, стремятся показать, что для решения задач с последовательными данными в качестве стартовой точки должен рассматриваться именно сверточный, а не рекуррентный поход, и, чтобы доказать свою точку зрения, предлагают общую и вполне прямолинейную модель Temporal Convolutional Network (TCN) и сравнивают ее с рекуррентными решениями на, что называется, «домашнем поле» последних, а именно датасетах, которые часто используются для сравнения качества рекуррентных моделей.

Да кто такой этот ваш TCN?

Пусть есть вход (x_0,…,x_T), из которого мы получаем элементы по одному, и каждый раз мы хотим получить некоторый выход y_t = f(x_0,…,x_t), то есть модель не умеет «заглядывать вперед во времени» и ее очередной выход должен зависеть только от входов, полученных к данному моменту. На уровне идеи модель TCN довольно проста, авторы начинают с операции одномерной расширенной (dilated) свертки:

Ее существенное отличие от привычной операции одномерной свертки состоит в том, что вместо индекса входа s-i берется s-d*i, то есть свертка берет предыдущие входы с некоторым «шагом». Параметр d так и называется фактором расширения (dilation factor), а k — это, собственно, размер фильтра.

Также стоит заметить, что свертка не центрирована, то есть индексы суммы не симметричны относительно нуля. Это вытекает из постановки задачи, которая запрещает нам «заглядывать вперед».

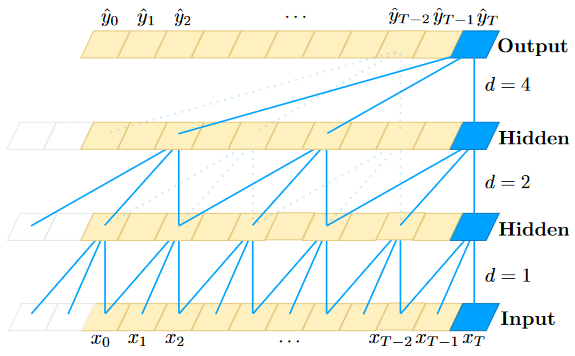
Благодаря расширенной свертке мы можем увеличить поле восприятия TCN как увеличением k, так и увеличением d, но, дабы мы случайно не «потеряли» какой-нибудь вход, рекомендуют экспоненциально увеличивать d от слоя к слою, как, например, на иллюстрации ниже.

Структура самого блока, соединяющего слои сети, вполне проста: берем расширенную свертку, делаем нормализацию весов, применяем нелинейность ReLU и делаем dropout, далее проделываем то же самое еще раз и суммируем с входом блока, прогнанного через фильтр размера 1 на 1. Ниже представлена иллюстрация и пример остаточного блока (замечание: свертка размера 1 на 1 необходима только в том случае, если вход и выход остаточного блока имеют различные размерности).

Выделим ряд преимуществ такой модели перед RNN:

• структура TCN позволяет сразу обучаться на всей последовательности, поскольку блок, который применяется на очередном слое, является общим для всего слоя (в частности, благодаря этому самой модели нужно меньше памяти);

• объем поля восприятия модели (следовательно и объем памяти, необходимый для модели) можно регулировать буквально тремя гиперпараметрами: числом слоев и величинами d и k, о которых мы уже поговорили;

• для TCN чужды взрывающиеся/затухающие градиенты, поскольку длина пути обратного распространения ошибки не зависит от длины входной последовательности.

Но стоит отметить, что TCN при генерации предсказания должна хранить в памяти все входные данные, в то время как RNN берет их последовательно и некое обобщение всех предшественников в ней хранится в скрытых векторах фиксированной длины. Также при переносе TCN с одной задачи на схожую, но требующую держать в уме более длинную историю, можно потерпеть неудачу и придется брать новые гиперпараметры.

Рубрика «эксперименты»

Итак, результаты TCN, с которым мы столько разбирались, сравнили с рекуррентной нейронной сетью (RNN) и ее модификациями: GRU и LSTM. Что же собой представляет «домашнее поле», о котором было сказано в самом начале? Тут и предсказывание следующей ноты в композициях И. С. Баха (JSB) и произведениях из коллекции Nottingham Music Database, и предсказывание следующего символа в текстах из датасетов PennTreebank и text8, и «игрушечные» задачи по обнаружению двух помеченных чисел в последовательности и нахождению их суммы (adding problem) и копированию начала последовательности в конец (copy memory), в общем, за описаниями датасетов с постановками задач и кодом моделей отсылаю читателя к репозиторию. Абсолютно в любом тесте TCN если не демонстрирует значительное превосходство, то хотя бы показывает сопоставимый результат. Ниже в подтверждение представлена таблица с результатами моделей на каждом датасете с указанием метрик, по которым модели сравниваются.

Но чему я удивился больше всего, так это тому, насколько хорошую точность выдал TCN на датасетах Sequential MNIST и Permuted Sequential MNIST при своей простоте! На Permuted Sequential MNIST модель TCN улучшила state-of-the-art, и этот результат был побит только спустя джва два года (!), а на Sequential MNIST без перестановок он уступил всего 0.2% точности Dilated GRU (опять же, идея с dilation-ом и тут помогла).

Датасет Sequential MNIST состоит из цифр MNIST, «вытянутых» из матрицы размером 28 на 28 в вектор длины 784, который подается модели на вход как последовательность. Датасет Permuted Sequential MNIST — это фактически Sequential MNIST, к каждому элементу которого применили одну и ту же перестановку (чтобы модели приходилось заучивать больше длинных зависимостей, ведь пиксели, которые раньше стояли рядом или хотя бы в одной строчке, могли оказаться по разные концы последовательности).

Стоит отметить, что TCN дает своим оппонентам фору и в скорости сходимости, вот, например, как меняется точность TCN, LSTM и GRU на тех же самых Seq. MNIST и Permuted MNIST за 10 эпох.

Также результаты на задании copy memory показывают, что TCN способен запомнить фактически сколь угодно долгую историю, в то время как GRU и LSTM — нет, и с увеличением расстояния, на которое по постановке задачи нужно скопировать начало ввода в конец вывода, они начинают просто гадать.

К чему я все это? Ах да, я хотел поделиться тем, чему меня научила эта статья. К любой задаче можно и нужно искать новые подходы, и рано или поздно это обязательно принесет плоды и найдется простая и гениальная модель, которая превзойдет все предыдущие!

Пост написан для курса СПбГУ по машинному обучению. Сам я являюсь студентом, поэтому открыт для исправлений, дополнений и обсуждений. В конце концов, век живи — век учись!