
В статье присутствуют Gif (трафик!) и контрастные картинки. У эпилептиков может случиться эпилептический припадок.
Для начала вспомним, что за «бильярдные фракталы».
Бильярдные фракталы.
Есть у нас некоторая прямоугольная область («бильярд»), в которой движется бильярдный шар (или луч света).

Шар упруго отражается от стенок по законам оптики (угол отражения равен углу падения). При этом шар бесконечно мал (абстрактная «материальная точка» из физики) и при движении и отражении скорости не меняет (скорость нас вообще не интересует).
Когда шар касается одной из выбранных стенок (не важно, какую стенку выбирать, но для примера выберем верхнюю) — фиксируем, в какую сторону движется шар — в левую или в правую:


Для бильряда, соотношение сторон которого — иррациональное число, последовательность отражений — фрактальная (насколько этот термин применим к двоичным последовательностям). Или фракталообразующая. Если визуализировать такую последовательность с помощью черепашьей графики, мы получим фрактал.
В качестве примера можем использовать последовательность для бильярда, соотношение сторон которого равно .
Строить такие последовательность очень легко:
Берем поочередно каждое целое число , умножаем на
, отбрасываем дробную часть и отмечаем четные целые части единицами, а нечетные — нулями.
let a=[]; for(let x=0;x<100;x++) a[x]=Math.floor(x*Math.sqrt(2))%2; console.log(a.join(''));
Первые 100 элементов этой последовательности:
0100110110010011001001101100110110010011011001101100100110010011011001001100100110110011011001001100
Визуализация этой последовательности с помощью черепашьей графики дает нам следующую фигуру:

Более подробно о том, откуда взялась эта формула и о визуализации последовательностей с помощью черепашьей графики, можно почитать во второй части — Фракталы в иррациональных числах
В реальном мире.
В реальном мире, такие последовательности встречаются гораздо чаще, чем может показаться на первый взгляд. Два примера.
Пример 1. Есть у нас два человека. Один побольше, второй — поменьше:

Эти два человека идут по улице. У высокого шире шаг, чем у низкого. Чтобы успевать за высоким, низкому приходится быстрее ногами двигать и больше шагов делать. В каждый момент времени, когда низкий ставит правую ногу на асфальт, фиксируем какая нога высокого находится в воздухе — левая или правая. Если частоты шагов низкого и высокого несинхронизированные — получим фрактальную последовательность.
Пример 2. Вокруг некоторой планеты вращается спутник:

Выбираем временной интервал произвольной длинны. Фиксируем в каком полушарии находится спутник в момент времени
— в южном или северном. Последовательность этих положений будет фрактальной, если соотношение длинны выбранного интервала с длинной интервала, за который спутник совершает полный оборот вокруг оси — иррациональное число.
Для наглядности, посмотрим на геометрическую интерпретацию бильярдных последовательностей.
Дискретизация линейной функции.
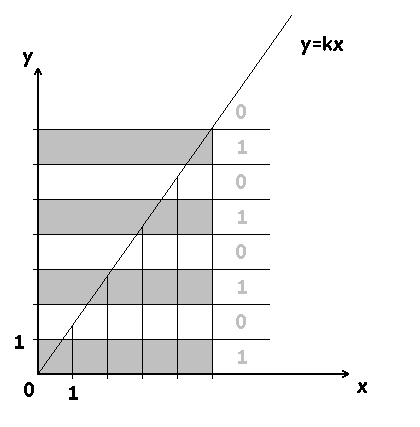
Для бильярда, соотношение сторон которого равно , строим график функции
. Целые числа, отмеченные на оси
, делят плоскость на чередующиеся полосы (поочередно помечаем полосы единицами и нулями). Целыми числами на оси
отмечаем, через какую полосу проходит график функции — через полосу помеченную единицей или нулем.
Фактически, все что мы сделали, чтобы получить фрактальную последовательность — дискретизировали линейную функцию с иррациональным коэффициентом . Если фрактальную последовательность можно получить дискретизацией линейной функции, первым делом напрашивается вопрос — а какую последовательность можно получить дискретизацией нелинейной функции?
Но прежде, чем переходить к нелинейным функциям, хотелось бы упомянуть об одном интересном наблюдении, сделанном в процессе написания статьи.
Об одном интересном наблюдении.
Возьмем нашу последовательность:
И построим из нее другую последовательность:
Первый элемент последовательности — произвольное число. Каждый следующий элемент — увеличиваем предыдущий элемент на 1, если соответствующий элемент первой последовательности () равен 1, или уменьшаем на 1 — если соответствующий элемент равен 0.
let a=[50]; for(let x=1;x<size;x++){ if(Math.floor(x*Math.sqrt(2))%2==1) a[x]=a[x-1]+1; else a[x]=a[x-1]-1; }
После чего можем построить фрактальную кривую, отметив на графике точки с координатами :
for(let x=0;x<size;x++){ context.fillRect(x, a[x], 1, 1); }

Из этой же кривой можем получить фрактальную поверхность. Для каждой точки считаем
.
Дальше можем сделать срез плоскости по оси :

Или отметить такие точки, для которых или

Следующая картинка — чем больше , тем ярче пиксель:

Можем немного изменить последовательность:
Раскрыв скобки, получим:
Здесь — дробная часть, которую мы ранее отбрасывали.
Как это выглядит в бильярдной модели? Мы увеличиваем предыдущий элемент последовательности на расстояние (по оси ) между правой границей и точкой касания шара верхней границы, если шар двигался влево. Или же уменьшаем на расстояние между левой границей и точкой касания шара верхней границы, если шар двигался вправо:
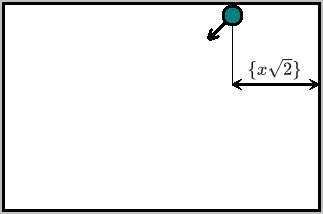
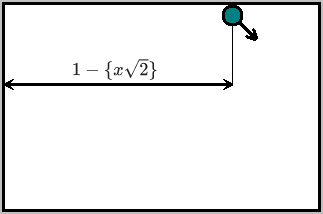
let c, arr=[0]; for(let i=1;i<size;i++){ c=i*Math.sqrt(2); if(Math.floor(c)%2){ arr[i]=arr[i-1]+(c-Math.floor(c)); }else{ arr[i]=arr[i-1]-(1-(c-Math.floor(c))); } }После раскрытия скобок:
let c, arr=[0]; for(let i=1;i<size;i++){ c=i*Math.sqrt(2); arr[i]=arr[i-1]+(c-Math.floor(c)); if(Math.floor(c)%2!=1){ arr[i]--; } }let c, arr=[0]; for(let i=1;i<size;i++){ c=i*Math.sqrt(2); arr[i]=arr[i-1]+(c-Math.floor(c)); }В этом случае поверхность получится гладкой, а не фрактальной.
Делаем визуализацию тем же способом, который использовали выше. Для каждой точки считаем
. Получили поверхность. Раскрашиваем. Чем больше
, тем ярче пиксель:

До того, как мы изменили последовательность, все были целыми числами. Теперь — иррациональные. Сделать
не получится. Но можем найти некоторую плоскость, которая находится на одинаковом расстоянии от максимальной и миниальной
и посмотреть на точки, которые лежат ниже и выше этой плоскости:

Самое интересное получится, если мы отметим пиксели, для которых . Другими словами, отмасштабируем
, умножив на некоторое число
, после чего отбросим дробную часть и проверим четность целой части. Для некоторых
:
478:

338:

Получаем замечательные круги. Примечательно, что круги получаем для равных числителю или знаменателю дроби, дающей приближенное значение
Для других :
144:

354:

Замечательные круги не получаем.
Здесь можно посмотреть в динамике, поводив мышкой по экрану.
Вернемся к дискретизации нелинейных функций.
Дискретизация нелинейной функции.
Например , где
— действительное число. Самый простой пример — парабола (
).
Строим последовательность:
let a=[]; for(let x=0;x<100;x++) a[x]=Math.floor(x*x*Math.sqrt(2))%2; console.log(a.join(''));
Для целых аргументов , записываем четность целой части (отбросив дробную) значения функции.
Первые 100 элементов этой последовательности:
0110010100111110000011000100010100000001010011010110001100101001010011111000000000100110111111111000
Визуализация этой последовательности с помощью черепашьей графики дает такую кривую:

Эта последовательность выглядит немного более хаотичной, чем последовательность, полученная дискретизацией линейной функции. Но это не так. Если где-то не видим закономерность — значит плохо смотрим. Можем сделать очень простую визуализацию. Запишем первые 1000 элементов последовательности в блокнот, включим перенос строк.

Можно разглядеть паттерн.
Для того, чтобы лучше разглядеть, единички заменяем на █, нолики — на ░:

Построим двухмерный график этой последовательности. На каждой следующей строчке последовательность сдвигается на
(где
— целое число, константа) позиций влево. Перепишем
как
.
Для некоторых :
35:

661:

Для можем раскрыть скобки, получим
. Получили уравнение поверхности.
Дискретизация поверхностей с ненулевой кривизной.
Для дальнейших экспериментов запишем уравнение в более общем виде:
Точно так же, как мы дискретизировали линейную функцию, мы можем дискретизировать поверхности второго порядка. Для этого считаем для каждого
и
, после чего умножаем
на иррациональное число, отбрасываем дробную часть, проверяем четность целой части —
Для наше уравнение принимает вид:
Это уравнение элиптического параболоида. Коэффициент определяет, насколько параболоид вытянут по оси
. Для
:
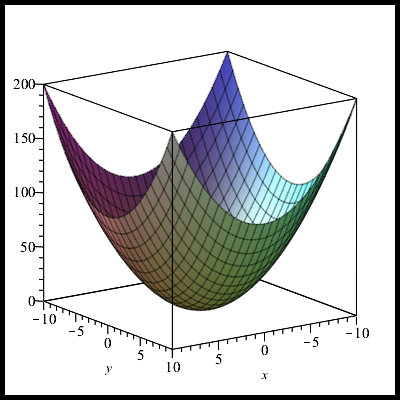
for(var x=0;x<canvas.width;x++){ xx=x-canvas.width/2; for(var y=0;y<canvas.height;y++){ yy=y-canvas.height/2; z=a*(xx**2+b*xx*yy+c*(yy**2))**(d); if(Math.floor(z*Math.sqrt(2))%2) context.fillRect(x, y, 1, 1); } }
Для получаем такой паттерн:

Можем этот же паттерн нарисовать недискретным. Вместо считаем
. Значение функции масштабируем (прибавляем 1, умножаем на 128) и используем в качестве яркости пикселя:

Для , дискретный и недискретный варианты:



Коэффициент сжимает или растягивает паттерн по оси
. Для
и
:


Коэффициент сжимает или растягивает паттерн по диагонали. Для
и
:


Дальше. Для наше уравнение принимает вид:
Это гиперболический параболоид — поверхность с отрицательной гауссовой кривизной:

Для :

Для :

Попробуем поменять степень . Для
наше уравнение принимает вид:
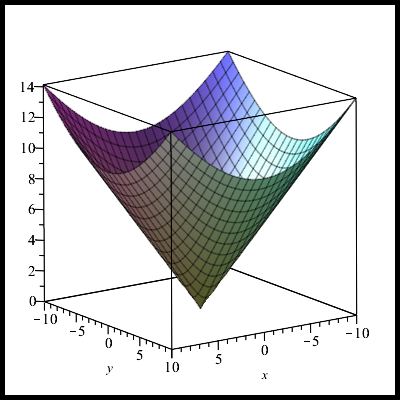
Для :

Для :

Для наше уравнение принимает вид:
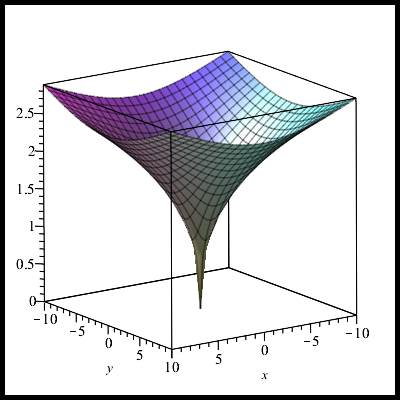
Для :

Для :

Для :

Самые интересные паттерны получаются, если взять такое , которое незначительно отличается от 1. Например для
:
Для паттерн похож на тот, что мы видели для элиптического параболоида:

Для :

Еще несколько примеров:
:

:

:

:

:

:

В статике — можем посмотреть дискретный и недискретный паттерны.
Подводя итоги…
Мы попробовали дискретизировать линейную функцию и получили фрактал. Если сделать срез трехмерной плоской волны поверхностью с ненулевой кривизной — получим голографический паттерн. Интересно, что мы получим, если сделаем срез четырехмерной плоской волны пространством с ненулевой кривизной? Об этом поговорим в другой раз.
ссылка на оригинал статьи https://habr.com/ru/post/595433/









Добавить комментарий