Нормали и обратное транспонирование, часть 3: внешняя алгебра над сопряжённым пространством

В двух предыдущих статьях мы научились рассматривать нормали в трёхмерном пространстве двумя разными способами: как бивекторы или как двойственные векторы. Обе интерпретации корректны, но они выражаются в различных единицах и по разному реагируют на преобразования.

В третьей и окончательной части мы отойдём от нормалей и рассмотрим некоторые другие интересные векторные величины. Мы видели как бивекторы и тривекторы из внешней алгебры выражают ориентированные площади и объёмы соответственно. Так же мы изучили двойственные векторы, которые действуют как ориентированные плотности линий в единицах обратных к длине. Теперь мы объединим эти геометрические концепции и посмотрим в какой степени они могут быть полезны. (В степени? Прямо как степень масштабного коэффициента? Ладно, забейте.)

Мы собираемся отправиться с места в карьер, потому если вам нужно освежить знания о внешней алгебре или двойственных пространствах, то пробегитесь по двум предыдущим статьям.

Внешнее произведение двойственных векторов

Внешняя алгебра позволяет брать внешнее произведение векторов, которое производит алгебраические сущности более высокого порядка, такие как бивекторы и тривекторы. По аналогии с обычными векторами можно сделать то же самое с двойственными векторами, получая двойственные бивекторы и двойственные тривекторы.

Двойственный бивектор получается из внешнего произведения двух двойственных векторов:

${\bf e_x^*}\wedge{\bf e_y^*}={\bf e_{xy}^*}$

а двойственный тривектор — из трёх:

${\bf e_x^*}\wedge{\bf e_y^*}\wedge{\bf e_z^*}={\bf e_{xy}^*}\wedge{\bf e_{z}^*}={\bf e_{xyz}^*}$

Это работает так же как внешнее произведение обычных векторов. В частности, выполняется тот же закон антикоммутативности.

Каков же геометрический смысл двойственных k-векторов? Вспомним что двойственный вектор определяется как линейная форма, то есть функция из некоторого векторного пространства в $\mathbb{R}$ . Внешнее произведение двойственных векторов оказывается изоморфным к двойственному внешнему произведению векторов. Для конечномерного можно записать:

$\bigwedge\nolimits^k{\left(V^*\right)}\cong\left(\bigwedge\nolimits^k V\right)^*$

где $\bigwedge\nolimits^k$ — операция конструирования набора k-векторов над данным векторным пространством.

В итоге, двойственные k-векторы можно понимать как линейные формы над k-векторами: двойственный бивектор является линейной функцией из пространства бивекторов в действительные числа, а двойственный тривектор — линейная функция из тривекторов в скаляры. Давайте детальнее разберёмся как это работает.

Двойственные бивекторы

В прошлой статье мы видели что двойственный вектор можно визуализировать как поле параллельных равноотстоящих плоскостей, представляющих линии уровней линейной формы:

Рисунок из Википедии: https://commons.wikimedia.org/wiki/File:N-form.svg

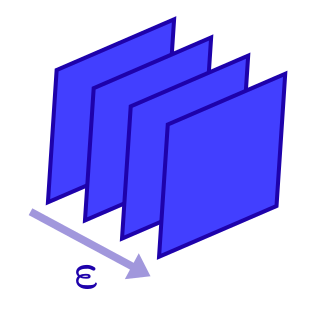
Расстояние между плоскостями на этой картинке отражает интервалы единичной величины на выходе линейной формы. Но всё же не забывайте, что фактически этих плоскостей бесконечно много и они непрерывно заполняют пространство по одной на каждое выходное значение линейной формы. Когда вы вычисляете значение линейной формы, то есть свёртываете двойственный вектор с вектором, результат показывает сколько плоскостей этот вектор пересекает от своего начала до конца (в непрерывном смысле слова «сколько»). Это зависит как от длины, так и от направления вектора: например, параллельный плоскостям вектор всегда вернёт единицу, вне зависимости от его длины.

Двойственный бивектор можно представить похожим образом, но вместо плоскостей будет поле параллельных прямых, равномерно распределённых на перпендикулярной к ним плоскости.

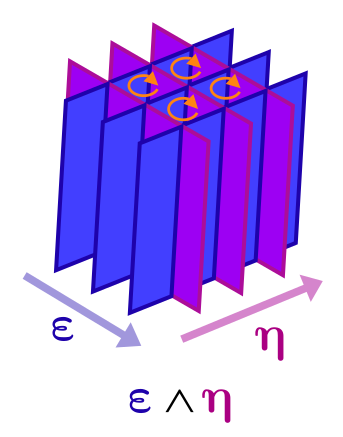
На этой диаграмме видно, что внешнее произведение двух двойственных векторов даёт двойственный бивектор, состоящий из всех прямых на пересечении плоскостей, соответствующих двум двойственным векторам.

Что произойдёт если свернуть этот двойственный бивектор с обычным бивектором? Как и раньше, получится скаляр, который теперь показывает сколько прямых пересекает бивектор! Если визуализировать бивектор как параллелограмм, или как круг, или как любую другую фигуру, у неё будет какая-то площадь. Потому она пересечёт какое-то количество непрерывного набора прямых. Это количество не будет зависеть от фигуры бивектора: напомним, что у бивектора нет определённой формы — у него есть только площадь (абсолютная величина) и ориентация. Бивектор, чья плоскость параллельна прямым, превратится в ноль вне зависимости от своей площади.

Так как двойственные векторы несут единицы обратной длины, а двойственный бивектор есть произведение двойственных векторов, двойственный бивектор соответствует единицам обратной площади. Он представляет ориентированную плотность по площади, например плотность вероятности на поверхности! Результат свёртки двойственного бивектора с бивектором сообщает насколько много вероятности (или ещё чего нибудь) покрывает площадь этого бивектора. Как подсказывает анализ размерности, двойственные бивекторы масштабируются как . То есть если вы увеличите масштаб объекта в раз, то плотность вероятности на его поверхности уменьшится в раз, потому что та же самая суммарная вероятность теперь распределена по большей в раз площади.

Что насчёт правила преобразования для двойственных бивекторов? В первой статье мы поняли что преобразование бивектора — это присоединённая матрица к (обозначим её $\mathbb{cof}(M)$ ). Во второй мы увидели что двойственные векторы преобразуются с помощью обратной транспонированной матрицы $(M^{-})^T$ . Отсюда следует что двойственные бивекторы преобразуются как $\mathbb{cof}((M^{-})^T)$ , или, что то же самое, $(\mathbb{cof}(M))^{-T}$ . Поразительно, но для матриц 3х3 эти формулы усыхают до

$M\over{\det{M}}$

То есть двойственные бивекторы преобразуются просто с помощью матрицы делённой на свой определитель.

Двойственные тривекторы

Продолжим следовать шаблону: если двойственные векторы в 3D выглядят как стопка параллельных плоскостей, а двойственные бивекторы выглядят как набор параллельных прямых, тогда двойственный тривектор выглядит как облако параллельных точек. Ну, опустим слово «параллельных», оно здесь ничего не значит. Это просто точки, равномерно расположенные в узлах пространственной решётки.

Как и ранее, внешнее произведение трёх двойственных векторов, или двойственного вектора и двойственного бивектора сооружает непрерывное облако точек из всех пересечений внешних сомножителей. Эта величина масштабируется как $1/{a^3}$ и выражает объёмную плотность. Если применить двойственный тривектор к тривектору, результат покажет какая величина облака точек заключена в объёме тривектора. Правило преобразования в этом случае простое: двойственный тривектор в трёхмерном пространстве всего лишь умножается на $1/\det{M}$ .

Ещё несколько тем

С вводом двойственных би- и тривекторов наш «зоопарк масштабов» наконец заполнен! У нас есть завершённая экосистема векторных величин со степенями масштабов от -3 до +3, каждая со своими единицами и соответствующей формулой преобразования.

Далее мы кратко затронем ещё несколько аспектов расширенной внешней алгебры с двойственными пространствами.

Внутреннее произведение

Как мы видели во второй части, векторное пространство и его двойственное пространство имеют «естественную свёртку» между векторами и двойственными векторами, похожую на скалярное произведение. Эта свёртка обобщается и на k-векторы с их двойственными векторами. Фактически, можно и дальше обобщать естественную свёртку так чтобы она работала с k-векторами и двойственными векторами разных степеней. Например, можно определить способ «свернуть» двойственный вектор с бивектором $B=u\wedge v$ таким образом:

$\langle w, B \rangle = \langle w, u \rangle v - u \langle w, v \rangle$

Геометрически получившийся вектор лежит в плоскости и направлен параллельно плоскостям уровней . В некотором смысле «съедает» размерность которая лежит вдоль направления плотности и оставляет остальные размерности в виде вектора.

Такое расширение операции свёртки называется внутренним произведением, хотя разные источники часто определяют его различными способами. Не будем сильно углубляться в эту тему. Основная идея в том что можно скомбинировать k-вектор с двойственным -вектором для любых k и , и получить (k-)-вектор, у которого отрицательные степени соответствуют двойственным векторам.

Звезда Ходжа

Вдобавок к двойственности векторных пространств о которой мы говорили, внешняя алгебра содержит ещё одно понятие двойственности: двойственность Ходжа, выраженную оператором под названием звезда Ходжа: $\star$ . (Обратите внимание, что символ отличается от обычной звёздочки $\ast$ , которой обозначалось двойственное пространство).

Понятие двойственности векторных пространств соотносит k-векторы с двойственными той же степени: векторы с двойственными векторами, бивекторы с двойственными бивекторами и т.д. Двойственность Ходжа работает иначе: она соотносит сущности с двойственными сущностями дополнительной (комплиментарной) степени. Применение звезды Ходжа к k-вектору создаст элемент степени , где — размерность пространства. В трёхмерном случае она заменяет векторы (степень 1) на бивекторы (степень 2), а скаляры (степень 0) на тривекторы (степень 3).

Я определю звезду Ходжа немного отличным от стандартного способом. Фактически есть две операции звезды Ходжа: одна переводит k-векторы в двойственные ()-векторы, а другая действует в обратном направлении. Я обозначу их как $\star$ и $-\star$ соответственно. Они взаимно обратны (как минимум в трёхмерном случае). Определяются они так:

$\star: \bigwedge\nolimits^k V \rightarrow \bigwedge\nolimits^{n-k} V^*: v^{\star}=\langle {\bf e_{xyz}^*}, v\rangle$ $-\star: \bigwedge\nolimits^k V^* \rightarrow \bigwedge\nolimits^{n-k} V^*: v^{-\star}=\langle v, {\bf e_{xyz}}\rangle$

Здесь угловыми скобками справа обозначено внутреннее произведение. То есть чтобы применить звезду Ходжа к k-вектору нужно взять его внутреннее произведение со стандартным единичным двойственным тривектором ${\bf e_{xyz}^*}$ (или единичным двойственным -вектором в -мерном случае). В результате получается двойственный -вектор, который геометрически представляет плотность по всем размерностям, не включенным в исходный k-вектор.

Чтобы сделать антизвезду Ходжа над двойственным k-вектором, нужно взять его внутреннее произведение с ${\bf e_{xyz}}$ , что даст -вектор, содержащий все размерности, не представленные исходным двойственным k-вектором, то есть все размерности, перпендикулярные к его плоскостям уровней.

Эти две операции почти определены на не связанных между собой областях, и потому могли бы быть объединены в одну «умную» звезду, которая автоматически определяет что делать в зависимости от типа аргумента… кроме случая k=0. Если применить эту звезду к скаляру, то во что он должен превратиться: в тривектор или в двойственный тривектор? Именно поэтому нужны две различные операции.

В трёхмерном случае интересен случай векторов, заменяемых на бивекторы:

Вектор под действием прямой звезды переходит в двойственный бивектор, чьи линии идут параллельно .
Бивектор под действием прямой звезды переходит в двойственный вектор, плоскости уровня которого параллельны .
Двойственный вектор под действием обратной звезды переходит в бивектор, параллельный плоскостям уровней .
Двойственный бивектор под действием обратной звезды переходит в вектор, параллельный линиям .

Несмотря на некоторую запутанность формального определения, видно что геометрический результат операций Ходжа довольно прост. Всё строится на переходах от геометрии k-вектора и соответствующих поверхностей уровня к геометрии двойственного -вектора и наоборот. Звёзды Ходжа очень полезны при работе со значениями из внешней и двойственной внешний алгебры.

Скалярное произведение (в обобщённом смысле), или забываем про двойственность

В большинстве трактовок внешней или геометрической алгебры двойственные пространства почти не упоминаются. Более общепринятое определение звезды Ходжа напрямую взаимно отображает k-векторы и -векторы без всяких двойственных. Как это работает?

Оказывается, если на нашем векторном пространстве определено некоторое скалярное произведение, то с его помощью можно переходить туда и обратно между векторами и двойственными векторами, или между k-векторами и их двойственными векторами.

До сих пор мы не вводили никакого способа отобразить отдельный вектор из основного в двойственное пространство, и наоборот. Хотя они и являются векторными пространствами одинаковой размерности, между ними не существует естественного изоморфизма. Тем не менее, наличие скалярного произведения обособляет замечательный изоморфизм основного пространства с двойственным. Им будет изоморфизм, который отображает вектор в двойственный вектор , определяя внутреннее произведение как обычное скалярное произведение.

Более формально, для всех векторов $u\in V$ определим $\langle v^*, u \rangle = v \cdot u$ . Это определение может быть расширено на внутренние произведения и изоморфизмы для всех k-векторов (подробности в Википедии).

Заменим, что это отображении не сохраняется при масштабировании и преобразованиях вообще, потому что преобразуется оператором $M^{-T}$ , а оператором .

Имея такое соответствие можно во многом игнорировать существование двойственных пространств и двойственных элементов. Можно воображать что они не отличаются от основных элементов. В ортонормированном базисе даже координаты вектор.а и его двойственного вектора будут одинаковыми.

Вот пример «забывания» о двойственных сущностях: звёзды Ходжа можно определить с помощью скалярного произведения чтобы незаметно перевести в сопряжённое пространство их аргументы или значения. Тогда две определённых выше звезды Ходжа схлопнутся в одну операцию, отображающую между $\bigwedge\nolimits^k V$ и $\bigwedge\nolimits^{n-k} V$ .

Какая от всего этого польза?

Пользы довольно много. Мы начали только с векторов и нормалей — двух векторообразных вещей с различными правилами, и это различие сбивало с толку. Но теперь у нас есть четыре сущности: векторы, двойственные векторы, бивекторы и двойственные бивекторы. Помимо этого возникли ещё и три скаляроподобных объекта: истинные безразмерные скаляры, тривекторы и двойственные тривекторы.

Очевидно, много людей спокойно живут даже не подозревая обо всех этих различиях! Даже статьи о внешней или геометрической алгебре не всегда так глубоко погружаются в двойственность. Вместо этого они трактуют k-векторы и двойственные к ним как единую сущность, неявно используя определённый выше изоморфизм. Их различное поведение при трансформациях становится всего лишь занятным фактом, частью бессистемного орнамента. Взамен такой подход требует чтобы некоторые элементы алгебры имели скалярное произведение или метрику, и это правильно работает только в ортонормированном базисе. Напротив, если «приправить» теорию двойственностью, то можно вывести формулы которые правильно работают в любом базисе.

В качестве небольшого примера рассмотрим конкретную задачу из графики. Допустим у нас есть меш из треугольников, и мы хотим выбрать на нём случайную (в смысле равномерного распределения по поверхности) точку. Чтобы это сделать, нужно выбрать случайный треугольник с вероятностью, пропорциональной площади. Обычно для этого предрассчитывают площади всех треугольников и строят таблицу с префиксными суммами. Далее для выбора треугольника достаточно взять равномерно распределённую случайную величину и найти ближайшее к ней значение в таблице бинарным поиском.

Внесём в задачу немного разнообразия. Что если меш преобразован, возможно неоднородным масштабированием или скосом? В общем случае преобразование изменяет площади треугольников в зависимости от ориентации. Равномерное распределение в пространстве модели (локальном пространстве меша) больше не будет равномерным в мировом пространстве. Можно было бы преобразовать весь меш в мировое пространство и сделать выборку уже в нём, но это слишком дорого.

Бивекторы приходят на помощь! Вместо предрассчёта скалярной площади каждого треугольника можно рассчитать бивектор, представляющий его площадь и ориентацию. Для треугольника с вершинами , , это будет ${1\over {2}} (p_2-p_1)\wedge (p_3-p_1)$ . Далее прерьразуем все бивекторы в мировое пространство с помощью подходящего правила, и они будут представлять площади преобразованных треугольников. Наконец рассчитаем их абсолютные значения и построим таблицу префиксных сумм.

Задачу можно решить и в обратную сторону. Допустим, у нас есть неоднородная вероятностная мера, определённая на треугольной сетке. Например, это может быть источник света с текстурой, определяющей силу излучения, и нам нужно выбрать точку с учётом силы излучения. Или может нужно выбрать с учётом телесного угла в заданном направлении, или ещё с какой нибудь мерой визуальной важности. Эти плотности вероятностей можно представить как двойственные бивекторы, и преобразовывать их в мировое пространство и обратно в локальное. Даже под воздействием неортогональных преобразований меша распределение будет сохраняться.

Ещё несколько примеров где возникают двойственные k-векторы:

Производная (градиент) скалярного поля (например SDF) является двойственным вектором по своей природе.
Пространственные частоты (волновые векторы) в анализе Фурье — двойственные векторы.
Переносимая лучом энергетическая яркость (radiance) является плотностью, удельной по площади проекции. Потому её хотя бы частично можно выразить двойственным бивектором.

Как и многие другие математические концепции, эти вещи полезны больше для усовершенствования ваших мысленных моделей геометрии, улучшения мыслительного процесса и для вывода формул которые можно использовать в коде более традиционным способом. Я не утверждаю, что нам всем нужно срочно бежать и переписывать классы математических библиотек на k-векторы и двойственные к ним. Хотя если честно, в математических библиотеках творится тот ещё бардак.

Причёсываем зоопарк

Перед завершением дам вам ещё немного пищи для размышлений. Выше мы увидели целый «зоопарк масштабирований» математических конструкций с различным поведением, различной геометрической и физической интерпретацией. Разные области естественных наук и математики по разному упорядочивают этот зоопарк, по разному осмысляют его обитателей и отношения между ними.

В компьютерных науках мы склонны понимать векторы, бивекторы и двойственные векторы как различные типы. У каждого из них может быть внутренняя структура, состоящая из более простых величин (действительных чисел), и набор разрешённых операций, который определяет что с ними можно делать и как они друг с другом взаимодействуют.

Тем временем, физики обычно исповедуют более прямолинейный подход. Геометрические элементы они понимают как матрицы действительных (иногда комплексных) чисел в связке с правилами преобразований, которые говорят что произойдёт с данной матрицей при замене координат. Алгебраические свойства (например, антикоммутативность) получаются через конструирование матриц таким образом, чтобы матричное умножение реализовывало нужную алгебру. Например, бивектор можно представить антисимметричной матрицей. Внешнее произведение двух векторов и даёт бивектор, соответствующий вычислению матрицы

У этого выражения есть то же свойство антикоммутативности, что и у внешнего произведения. Умножение этой матрицы на (двойственный) вектор представляет внутреннее произведение бивектора на . Двойственный бивектор по структуре будет точно таким же, но у него будет другой закон преобразования («ковариантный» а не «контравариантный»).

Наконец, математики формализуют этот зоопарк относя различные геометрические значения к различным пространствам и/или алгебрам. Оба этих термина в конечном итоге означают «множество» (в теоретико-множественном смысле), снабжённое какой-то дополнительной структурой: алгебраическими операциями, топологией, нормой или метрикой, и т.п. Конкретная структура зависит от того что именно вы делаете. Таких структур существует огромное количество, и они используются в самых разных контекстах.

Так какая структура стоит за зоопарком масштабирований? У нас есть структура векторного пространства и есть внешняя алгебра. Но ни то ни другое не отражает всего разнообразия масштабирований и преобразований двойственных элементов: двойственные пространства изоморфны своим исходным пространствам (в конечномерном случае), а то и полностью идентичны им.

У меня ещё нет проработанного ответа, но я подозреваю что он лежит где-то в теории представлений групп Ли. Мне кажется что разные типы масштабирований могут быть закодированы как векторные пространства, на которые подействовали разными представлениям группы , то есть группы Ли всех линейных отображений на $\mathbb{R}^n$ . В общем, не будем углубляться в эту тему. Для более подробного изучения есть пара хороших ссылок: раз, два. Ещё есть книга о роли теории представлений в практической физике.

Заключение

Я надеюсь это было увлекательное и полезное путешествие через глубинные слои нашей любимой евклидовой геометрии. Мы начали с простого вопроса: почему векторы нормалей нужно преобразовывать обратной транспонированной матрицей? И увидели что существует намного более богатая структура чем видно на поверхности.

«Зоопарк масштабирований» k-векторов и двойственных к ним получился полным и симметричным. Хоть я и не применяю эти вещи на практике каждый день, их изучение помогло мне понять вещи, которые раньше я осознавал весьма смутно и расплывчато. Осознание существования этих тонких различий того стоило. В жизни я всегда руководствуюсь тем что всё вокруг более сложно чем кажется на первый взгляд, и нигде это правило не проявляется так ярко как в математике!

ссылка на оригинал статьи https://habr.com/ru/post/669734/