Введение в суррогатные модели. Часть 3: Выходим в топ

Продолжаем серию постов об одном очень полезном методе из мира машинного обучения, цель которого – существенно ускорить инженерное проектирование. Мы с вами уже научились обучать легкие модели на замену мощным и детальным инженерным пакетам для симуляции сложных систем. Теперь научимся делать так, чтобы новые суррогатные модели точно отражали изучаемое явление в нужных пределах, но при этом требовали как можно меньше данных и быстро обучались. Тема супер интересная, поэтому мы сделали перевод отличной статьи авторства Шуая Гуо, и на ее основе делимся своим опытом и кодом на MATLAB, чтобы вы могли все попробовать сами.

В первой части этой серии статей мы познакомились с фундаментальными понятиями суррогатного моделирования. Во второй – изучили, как реализовать метод суррогатного моделирования на конкретном примере, прошли по всему процессу создания такой модели.

Метод суррогатного моделирования, напомним, позволяет подготовить быстродействующую (а значит «недорогую», но точную) статистическую модель, которая будет использована взамен дорогостоящей симуляции, что значительно снизит временны́е затраты на проектирование сложной системы и поднимет шансы наути более успешное решение в ходе аналитической фазы создания продукта.

В части III мы кратко обсудим следующие три приема, которые крайне важны для создания и исследования суррогатных моделей:

• Градиентные суррогатные модели: использование градиентов в обучающей выборке позволяет получать более точные модели;

• Суррогатные модели смешанной точности: совместное использование обучающих данных различного уровня детализации для повышения эффективности обучения;

• Активное обучение: интеллектуальное обучение суррогатных моделей путем активного выбора обучающих данных.

1. Градиентные суррогатные модели

1.1 В чем идея

Градиент – это степень чувствительности выходных переменных модели к изменениям во входных переменных. Благодаря удобству современных методов численной оптимизации во многих сферах сегодня используются быстрые и эффективные приемы симуляции, такие как оптимизация сопряженных направлений (и сопряженных моделей, в том числе суррогатных) или, конечно, автоматическое численное дифференцирование. В последнее время для программ инженерного моделирования стало обычным делом предоставлять проектировщику не только вычисление выходов модели f(x) для входного вектора x, но и, в силу низкой затратности, заодно выдавать и градиенты ∂f(x)/∂x. Итак, зачем они нам?

Дело в том, что мы можем использовать градиенты как дополнительный источник данных, то есть и расширить состав нашего обучающего датасета от пары значений (xᵢ, f(xᵢ)) до группы (xᵢ, f(xᵢ), ∂f(xᵢ)/∂xᵢ). Дополнительная информация о градиентах позволяет нам, не увеличивая количество примеров в обучающем датасете, добиться более высокой точности суррогатной модели по сравнению с обучением без градиентов.

Еще одно преимущество градиентного подхода: для достижения той же заданной точности ему нужно меньше входных данных. Это очень полезно на практике. Вспомним, что для генерации каждой обучающей точки данных нам требуется один раз прогнать дорогостоящий код детальной модели системы или процесса. Если мы можем обойтись меньшим количеством обучающих данных, то сможем обучить суррогатную модель, потратив меньший вычислительный бюджет, что повышает эффективность обучения.

1.2 Пример

Давайте на примере посмотрим, как суррогатная модель с градиентами может еще больше повысить точность прогнозирования. В этом примере для аппроксимации функции, изображенной на рис. 1 мы обучим обычную модель с гауссовским процессом, а потом реализуем градиентный метод.

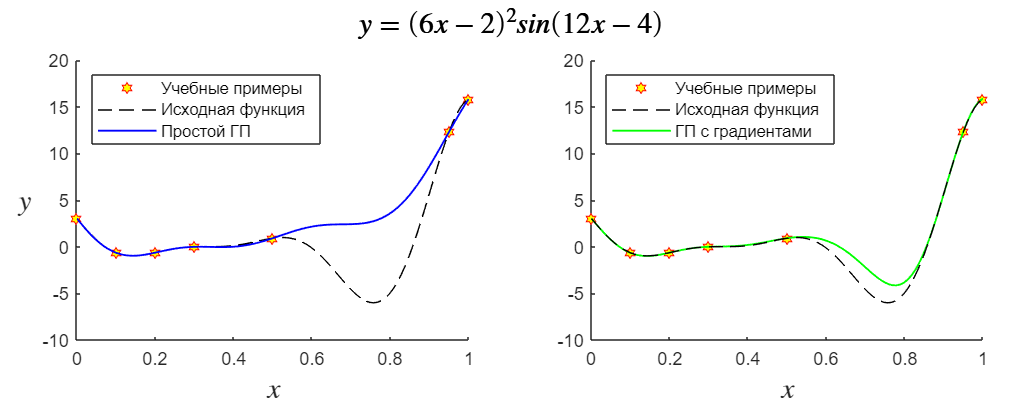
Обе суррогатные модели используют одну и ту же обучающую выборку, но обучение градиентной модели задействует еще и производную выходной переменной y по входу x.

Мы показываем довольно простой метод учета градиентов, который легко воплотить стандартными средствами MATLAB (т.н. «косвенный метод»). Как видно из кода, мы используем только первые производные. Местами утверждается, что этот метод также более эффективен в вычислительном плане (что легко понять, ведь это просто аугментация датасета без вмешательства в ход оптимизации модели).

% Запомним значения «истинной» функции X = linspace(0,1,100); [y, dy] = f(X);  % Создаем тренировочный датасет, обучим модель и получим оценку X_train = [0 0.1 0.2 0.3 0.5 0.95 1]; [y_train, dy_train] = f(X_train); gprMdl_no_grad = fitrgp( X_train', y_train' ); y_test = predict( gprMdl_no_grad, X' );  % Создаем тренировочный датасет с градиентами (модель, оценка) [X_train_grad, y_train_grad] = apply_grad(X_train, y_train, dy_train); gprMdl_with_grad = fitrgp( X_train_grad', y_train_grad' ); y_test_grad = predict( gprMdl_with_grad, X' );  figure; plot(X, y_test, 'b', 'LineWidth',1); hold on; plot(X_train, y_train, 'rh'); plot(X, y_test_grad, 'g', 'LineWidth',1); plot(X, y, 'k--'); legend('Учебные примеры', 'Исходная функция', 'Простой ГП', ...     'ГП с градиентами', 'Location','northwest')  % Функция, которую мы аппроксимируем (и её производная) function [y, dy] = f(X)     y = (6.*X - 2).^2 .* sin(12.*X - 4);     dy = 24 * (3.*X - 1) .* (sin(12.*X - 4) + (6.*X - 2) .* cos(12.*X - 4)); end  % Создание датасета с новыми точками (косвенный учёт градиентов) function [X, Y] = apply_grad(x_in, y_in, dy_in)     % Шаг прироста аргумента функции будет 1/100 от мин.расстояния между точками     step_x = abs((max(x_in) - min(x_in)) / 100);     X = [x_in - step_x; x_in; x_in + step_x]; X = X(:)';     Y = [y_in - dy_in.*step_x; y_in; y_in + dy_in.*step_x]; Y = Y(:)'; end

По результатам, представленным на рис. 1, отлично видно, что версия суррогатной модели с градиентами обладает гораздо большей точностью, чем базовая версия. Особенно в области значений около x = 0.8. Несмотря на то, что в этой области вообще нет учебных примеров, модель с градиентами все равно почти отразила зависимость близко к исходной функции (и мы использовали только производные первого порядка).

1.3 Вызов

Основная проблема, ограничивающая применение суррогатных моделей с градиентами – это взрывной рост количества данных в датасете.

Во-первых, количество учебных данных растет экспоненциально с увеличением числа входных параметров. Предположим, что имеется 2 входных параметра и мы используем 10 обучающих примеров для обучения суррогатной модели. В этой ситуации совокупный объем учебных данных составляет 30 элементов:

Теперь предположим, что нам нужно учесть в общей сложности 4 входных параметра. Поскольку количество входов увеличилось, суррогатная модель, наверное, станет сложнее, и нам потребуется больше примеров для ее обучения. Допустим, мы используем 20 примеров. Теперь набор обучающих данных насчитывает 100 элементов:

Таким образом суммарное количество обучающих данных растет очень быстро с ростом количества входных параметров. Наличие большого количества обучающих данных не всегда хорошо для проекта, поскольку замедляет процесс настройки модели (т.е. оптимизацию гиперпараметров). В конце концов обучение суррогатной модели может занимать даже больше времени, чем проведение высокоточной симуляции (что даже может сделать постоянную оптимизацию гиперпараметров суррогатной модели просто нерентабельной).

Во-вторых, теоретически, в датасет для суррогатной модели можно включить производные и более высокого порядка. Это также приводит к взрывному росту количества данных: количество частных производных, используемых при обучении модели, тоже растет экспоненциально по мере повышения порядка дифференцирования. Например, при двух входных параметрах x₁ и x₂ производные первого порядка содержат только два термина (т.е., ∂f/∂x₁ и ∂f/∂x₂), а производные второго порядка содержат еще 3 термина (т.е. ∂f²/∂²x₁, ∂f²/∂²x₂ и ∂f²/∂x₁∂x₂), следовательно, вместе в каждом наборе данных (x₁, x₂, y) нашей одномерной функции нам нужно будет хранить еще 5 чисел.

Чтобы справиться с проблемой взрывного роста количества данных, нужно осторожнее отбирать, какие производные от каких переменных попадут в датасет. Такие методы отбора правильного состава производных, которые позволяли бы снизить общую трудоемкость обучения, представляют собой область активных исследований.

2. Суррогатные модели смешанной точности

2.1 Основная идея

В области инженерных вычислений часто бывает, что для получения результата можно воспользоваться несколькими разными решателями (разными программами моделирования) с разной точностью оценки и скоростью работы.

Высокоточные модели выдают данные о моделируемом процессе с более высоким пространственно-временным разрешением. Их результаты больше соответствуют реальности, но и вычислительные затраты на их выполнение также более высоки. На другом конце спектра находятся модели с низкой точностью, которые обычно имеют более грубое пространственно-временное разрешение и не включают тонкие физические детали. Однако они выполняются гораздо быстрее, чем их высокоточные аналоги.

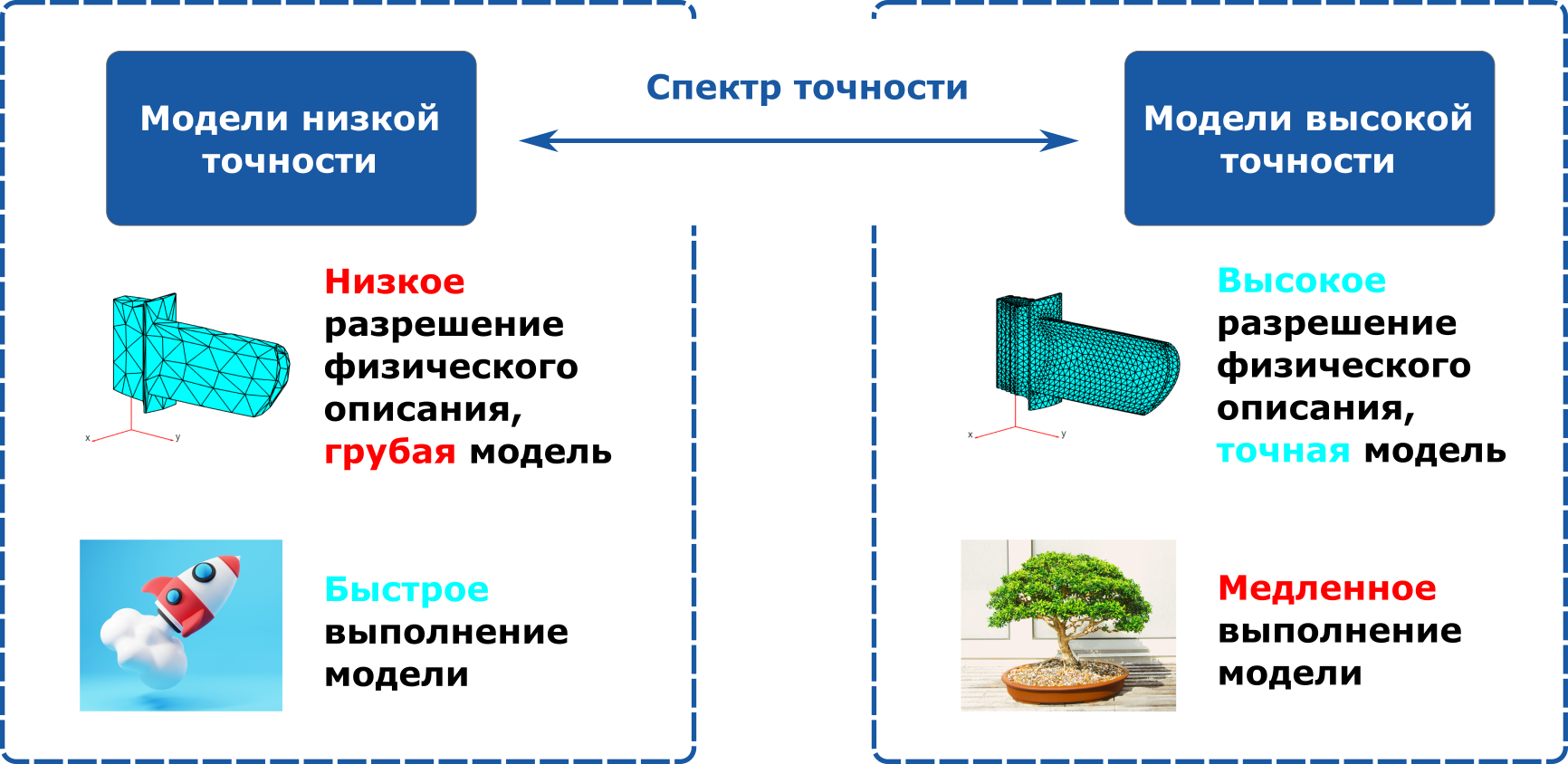
Естественно, мы хотели бы, чтобы наши суррогатные модели позволяли получать результаты той же точности, что и высокоточная симуляция. И, как мы знаем, наполнить датасет для высокоточной суррогатной модели примерами, полученными путем прогона высокоточной симуляции может обойтись нам очень дорого. Как же добиться достаточной точности, при этом не тратя бюджет на обнаружение явно избыточных зависимостей?

Один из способов – получать лишь небольшое количество образцов высокой точности, но в то же время генерировать большое количество образцов низкой точности (чем быстрее выполняется «дешевая» неточная модель, тем для нас лучше). Объединяя в один датасет образцы разной степени точности мы можем минимизировать затраты на обучение максимально точной суррогатной модели.

Именно этого позволяет достичь стратегия смешанной точности. Если рассуждать по шагам, эта стратегия использует много «дешевых» данных низкой точности для исследования пространства параметров и получения качественно (но не количественно) верного описания общего тренда аппроксимируемой зависимости «вход-выход». Параллельно, стратегия задействует уже доступные образцы высокой точности, чтобы уточнить результаты, полученные на модели низкой точности, тем самым обеспечивая корректность количественных данных обученной суррогатной модели.

2.2 Пример

Рассмотрим, как можно использовать датасет смешанной точности для обучения суррогатной модели, пользуясь урезанным набором высокоточных обучающих примеров.

На рис. 3(a) показаны учебные выборки низкой и высокой точности, а также истинная функция, которую мы хотим аппроксимировать. Мы видим, что неточная модель плохо прогнозирует истинную функцию, которую мы аппроксимируем, ее прогнозы сильно смещены, поскольку не учитывают какой-нибудь параметр или эффект. При этом можно видеть, что они соответствуют истинной функции по форме, что нужно использовать для повышения эффективности обучения модели.

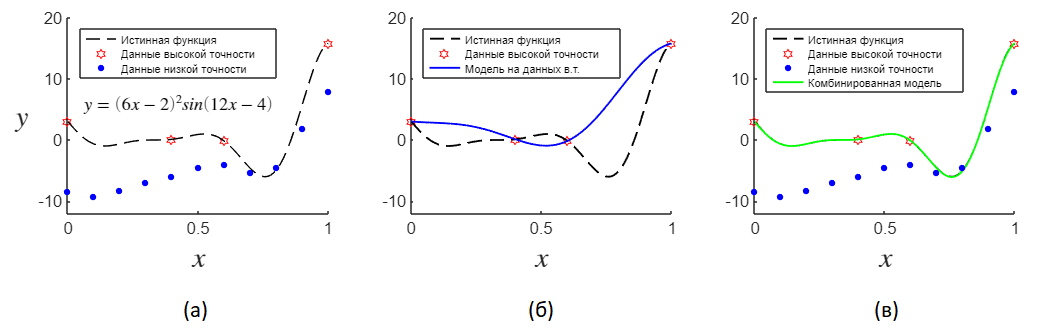
На рис. 3(б) мы видим, что одних только высокоточных обучающих примеров недостаточно для построения точной модели, поскольку подогнанная суррогатная модель не может передать характеристики истинной функции. На рис. 3(в), однако, видно что на основе низкоточной модели можно построить очень хорошую аппроксимацию путем добавления совсем небольшого количества высокоточных образцов.

Попробуйте запустить у себя этот код и поэкспериментировать с параметрами. Чтобы подробнее почитать про детали реализации, см. Selvakumar et al.

X = linspace(0,1,100);  % Данные дорогостоящей модели (e - expensive) X_train_e = [0 0.4 0.6 1]; [y_train_e, dy_train_e] = f_e(X_train_e); [X_train_e_grad, y_train_e_grad] = apply_grad(X_train_e, y_train_e, dy_train_e);  % Данные дешевой модели (c - cheap) X_train_c = linspace(0, 1, 11); [y_train_c, dy_train_c] = f_c(X_train_c); [X_train_c_grad, y_train_c_grad] = apply_grad(X_train_c, y_train_c, dy_train_c);  % Модель, обученная только на «дорогих» данных % Используется только для визуализации на графиках mdl_e = fitrgp(X_train_e', y_train_e'); y_test_e = predict(mdl_e, X');  % Данные с учетом производных будут использоваться при расчёте невязки mdl_e_grad = fitrgp(X_train_e_grad', y_train_e_grad'); y_test_e_grad = predict(mdl_e_grad, X_train_e_grad');  % Модель, обученная только на «дешёвых» данных mdl_c = fitrgp(X_train_c', y_train_c'); y_test_c = predict(mdl_c, X_train_e');  % Данные с учетом производных будут использоваться при расчёте невязки mdl_c_grad = fitrgp(X_train_c_grad', y_train_c_grad'); y_test_c_grad = predict(mdl_c_grad, X_train_e_grad');  % Параметр масштабирования для данных разного уровня точности, подбирается или оптимизируется p = 2;  % Модель, обученная на разнице y_d = y_test_e_grad - p .* y_test_c_grad; mdl_d = fitrgp( X_train_e_grad', y_d);  y_test_mix_part1 = predict(mdl_c_grad, X'); y_test_mix_part2 = predict(mdl_d, X'); y_test_mix = p .* predict(mdl_c_grad, X') + predict(mdl_d, X');  figure(); plot(X, f_e(X), 'k--', 'LineWidth',1); hold on plot(X_train_e, y_train_e, 'rh', 'MarkerSize',5); plot(X_train_c, y_train_c, 'bo', 'MarkerSize',3, 'MarkerFaceColor','b'); plot(X, y_test_e, 'b:', 'LineWidth',1); plot(X, y_test_mix, 'g-', 'LineWidth',1); legend('Истинная функция', 'Данные высокой точности', ...     'Данные низкой точности', 'Модель на данных в.т.', 'Комбинированная модель');  % Дорогостоящая точная модель function [y,dy] = f_e(X)     % В учебных целях оставляем здесь символьный вывод уравнений     syms xs     fcs = 0.5.*(6*xs - 2)^2 .* sin(12*xs - 4) + 10*(xs - 1);     dfcdx = diff(fcs,xs);     fes = 2*fcs - 20*xs + 20;     dfedx = diff(fes,xs);     % Нахождение значения функции и ее производной     y = double(subs(fes, xs, X));     dy = double(subs(dfedx, xs, X)); end  % Неточная дешевая модель function [y,dy] = f_c(X)     % В учебных целях оставляем здесь символьный вывод уравнений     syms xs     fcs = 0.5.*(6*xs - 2)^2 .* sin(12*xs - 4) + 10*(xs - 1);     dfcdx = diff(fcs,xs);     fes = 2*fcs - 20*xs + 20;     dfedx = diff(fes,xs);     % Нахождение значения функции и ее производной     y = double(subs(fcs, xs, X));     dy = double(subs(dfcdx, xs, X)); end  function [X, Y] = apply_grad(x_in, y_in, dy_in)     step_x = abs((max(x_in) - min(x_in)) / 100);     X = [x_in - step_x; x_in; x_in + step_x]; X = X(:)';     Y = [y_in - dy_in.*step_x; y_in; y_in + dy_in.*step_x]; Y = Y(:)'; end

Похоже, наиболее ранняя статья, где цитирируется этот конкретный пример, была выполнена Forrester et al. (2007), а в качестве наиболее раннего автора этого метода цитируется в Morris et al (1993). Чтобы правильно реализовать эти методы, нам потребовалось пройтись по статьям, зато теперь вы можете запустить код и посмотреть, что будет если оставить всего 2 точки из датасета «высокоточной» модели. Обещаем, что вы удивитеcь. 🙂

3. Активное обучение

3.1 Основная идея

Плати меньше — получай больше.

При построении суррогатной модели желательно использовать как можно меньше обучающих данных, добиваясь при этом заданной целевой точности модели. Напомним, что создание каждого примера для обучающего датасета предполагает проведение дорогостоящей компьютерной симуляции. Таким образом, снижение количества обучающих данных всегда означает повышенную экономическую эффективность синтеза суррогатной модели.

Ранее мы стремились к тому, чтобы выборка равномерно покрывала пространство параметров, что гарантировало бы, что в данных не будет пропусков, а значит модель будет точнее. Однако такая практика может привести к значительному перерасходу вычислительных ресурсов: аппроксимированная зависимость «вход-выход», как правило, не является одинаково «сложной» во всех точках пространства параметров, поэтому не все области этого пространства должны быть представлены равным количеством обучающих данных.

Вместо этого более разумным способом было бы обогащение набора обучающих данных по мере обучения. Таким образом, суррогатная модель получает возможность активно исследовать ландшафт аппроксимированной зависимости «вход-выход» и добавлять выборки в тех областях, где, по мнению модели, ее прогнозы неточны.

Функция отбора объектов играет ключевую роль в задаче активного обучения, поскольку она определяет, какую точку нужно добавить к текущему набору данных для наиболее выгодного обучения. Разработка действенных подходов для отбора объектов является активной областью исследований. У разных функций отбора могут быть разные цели – например, максимизация влияния на модель или отбор по несогласию в комитете (здесь чуть больше информации).

Далее мы рассмотрим одну конкретную функцию обучения, целью которой является построение суррогатной модели, одинаково точной во всем пространстве параметров. Эта функция обучения необходима, когда планируется использовать обученную суррогатную модель для проведения параметрических исследований, анализа чувствительности и визуализации зависимости «вход-выход».

3.2 Ожидаемая ошибка предсказания (EPE)

Эта функция отбора указывает нам следующую точку в пространстве параметров, где суррогатная модель имеет наибольшую ожидаемую ошибку предсказания. Интуитивно понятно, что добавляя именно такие точки в датасет мы должны обеспечить суррогатной модели самый быстрый ход обучения.

В машинном обучении ожидаемая ошибка предсказания может быть записана как комбинация компоненты смещения или тренда и компоненты дисперсии. Это хорошо известная всем декомпозиция смещение-дисперсия:

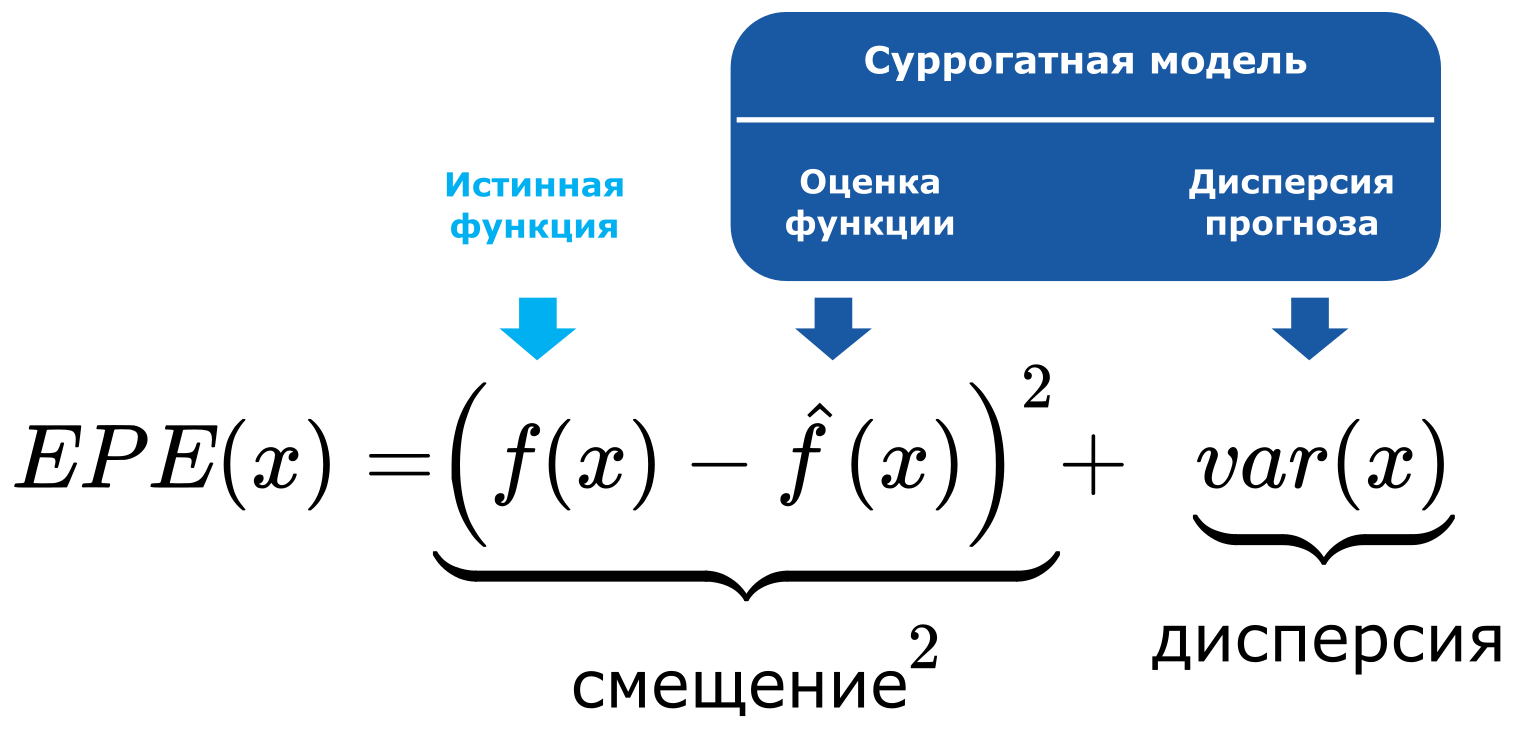
Чтобы использовать эту функцию, нужно чтобы используемая суррогатная модель могла оценивать неопределенность своего прогноза (т.е. свою дисперсию). Одним из видов суррогатных моделей, удовлетворяющих этому требованию, является гауссовский процесс.

Очевидно, что мы не можем заранее знать истинное значение функции f(x) (иначе нам не нужно было бы строить суррогатную модель для ее аппроксимации!). Поэтому компонент дисперсии в вышеприведенном уравнении может быть только результатом оценки. Одним из способов сделать это является кросс-валидация. Детали реализации такого подхода можно найти в работе Liu et al.

4. Основные выводы

Мы рассмотрели некоторые продвинутые приемы суррогатного моделирования:

• Градиентные суррогатные модели, использующие при своем обучении производные выходных переменных относительно входных для повышения точности прогноза.

• Суррогатное моделирование смешанной точности – метод, который позволяет обучить высокоточную модель, используя минимум высокоточных учебных данных и множество данных заведомо низкой точности (отражающих зависимость качественно, но не количественно), что еot больше снижает требования к необходимым вычислительным ресурсам.

• Активное обучение, как более сложный метод обучения суррогатной модели, побуждающий нас активно исследовать пространство параметров и находить области, в которых расположены такие образцы, добавление которых в обучающую выборку обеспечит модели наибольший прирост знаний о моделируемой системе.