Коэффициент однозначности

Идея проста. Наблюдаем последовательность состояний. И требуется оценить насколько эта последовательность предсказуема. 

Пусть с равной вероятностью следуют состояния 1 и 2. Этой последовательностью может быть [ 1, 2, 1, 1, 2, 2, 1, 2, 2, 1]. Можем ли мы однозначно предугадать следующее состояние? По этой информации — нет.

Теперь допустим, что есть ещё одна последовательность [3, 4, 4, 3, 3, 4, 3, 3, 4], синхронная первой. Её можно интерпретировать так: 

3:1->2 (если 3, то 1 переходит в 2) 4:2->1 (если 4, то 2 переходит в 1) 4:1->1 (если 4, то 1 переходит в 1) 3:2->2 (если 3, то 2 переходит в 2).   [1, 2, 1, 1, 2, 2, 1, 2, 2, 1] [3, 4, 4, 3, 3, 4, 3, 3, 4,  ]

Мы по прежнему не знаем каким будет состояние после состояния 1 (последнее в списке). Но, если будет известно, что следующим после 4 будет 3, то последует 2.

Очеловечим рассуждения. Представим себе, что вошли в комнату и целью является включить свет. Обозначим: 1 — свет не горит, 2 — свет  горит. Меняем состояние выключателя на включение 5 и на выключение 6). Пусть эта последовательность такова [5, 6, 5, 6, 5, 6, 5, 6, 5]. 

 [1, 2, 1, 1, 2, 2, 1, 2, 2, 1]  [5, 6, 5, 6, 5, 6, 5, 6, 5,  ]

Имеем при действии 5 (включить): состояние 1 переходит  в состояние 2 (свет есть); но также состояние 1 перейдёт в состояние 1 (света нет) при этом же действии, т.е. 5:1->2|1. Что это значит? То, что смена состояний выключателя не приводит однозначно к целевому состоянию. 

Вопрос: может этим выключателем является нечто иное? Им может быть, например: 3 — книжка на нижней полке. 4 — она же на верхней полке.

Так как же, не зная заранее что на что влияет, количественно оценить предсказуемость следующих состояний? Введём коэффициент однозначности. Отнесем количество переходов, как если бы все переходы были однозначны,  к всем случившимся. Чем он ближе к единице, тем более предсказуема сменяемость состояний. Тем с меньшим количеством ошибок можно проложить оптимальный маршрут  к целевому состоянию.

Ниже код программы, который по имеющимся отдельным наблюдениям, может этот коэффициент однозначности рассчитывать для разных гипотез. 

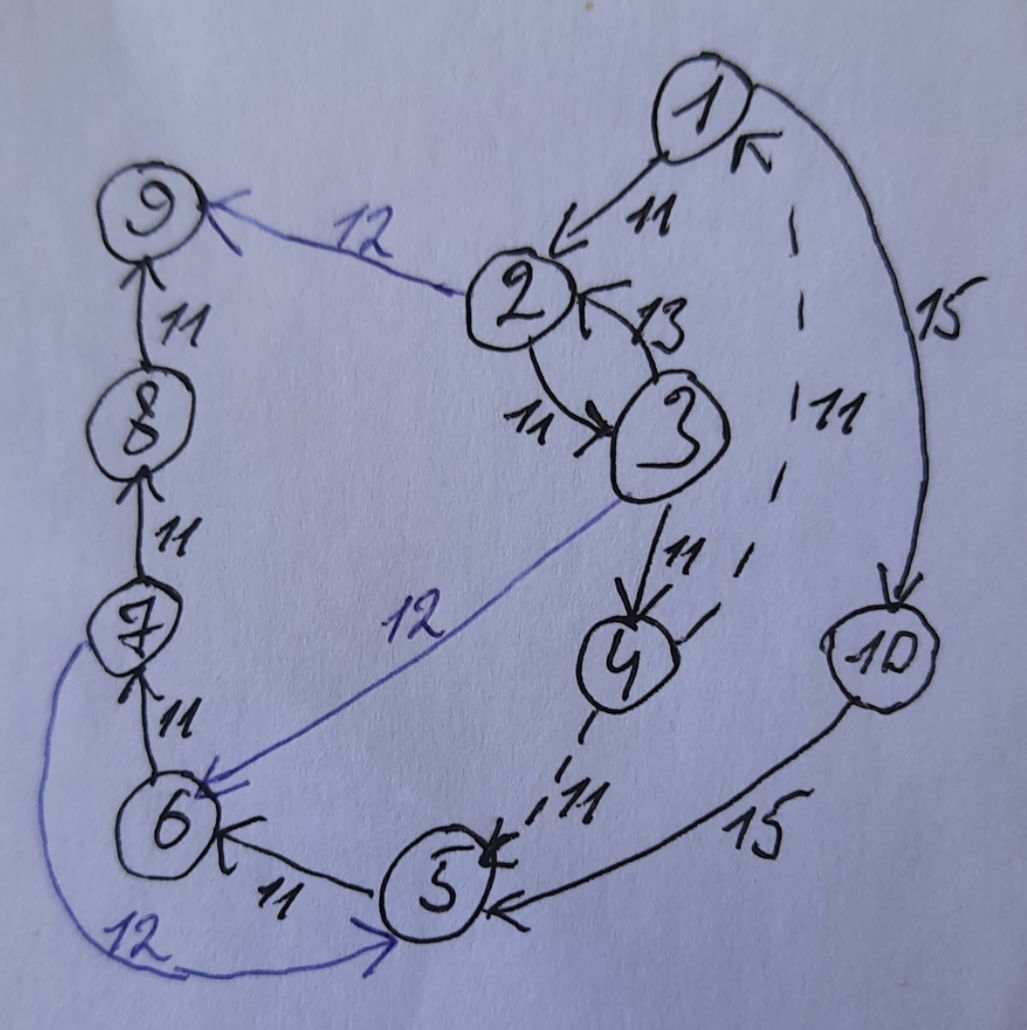
За объект исследования возьмем граф с некоторой неоднозначностью (из состояния 4 следует как состояние 5, так и состояние 1 при одном и том же действии 11).

Ниже красным — коэффициент однозначности оригинала. Зеленая (первая) гипотеза явно проигрывает синей (второй), поскольку ее коэффициент однозначности меньше.

Далее, учитывая вторую гипотезу, можно уже прокладывать маршруты к целевому состоянию.

import random import matplotlib.pyplot as plt import numpy as np  class Hd(): def __init__(self, graph): self.graph = graph  def rnd_get(self, v): return random.choice(v.split("|"))  def show(self, graph): for x in graph: print(x, ":", graph[x])  def get_ku(self, graph): '''return (коэффициент однозначности, размер)''' n = 0; u = 0 for x in graph: for y in graph[x]: if y[0]: u += y[0].count("|") n += 1 if n != 0: return (round(1- u/(n+u), 3), n)  else: return (None, None)  def get_states(self, x, f_list = [], n=10): x_list = [] x_list.append(x)  if f_list != []: for f in f_list: xf = [xf for xf in g[x] if xf[1] == f] if not xf: x_list.append(''); f_list[len(x_list)-2] = '' return (x_list, f_list[:len(x_list)-1]) x = self.rnd_get(xf[0][0]) x_list.append(x) else: for i in range(n): if not self.graph[x]: x_list.append(''); f_list.append('') break t = random.choice(self.graph[x]) f = t[1] x = random.choice(t[0].split('|')) x_list.append(x); f_list.append(f)  if len(f_list) == len(x_list) -1: return (x_list, f_list) else: return ([], [])  def get_yfx(self, f_list, x_list, t = True): if len(x_list)-1 != len(f_list): return []  path = [] for i in range(len(f_list)): path.append((x_list[i], f_list[i], x_list[i+1]))  if t: return path #(x, f, next_x) else: p = [] for xfy in path: if xfy[2] != '': p.append(xfy[2]+'='+xfy[1]+'('+xfy[0]+')') return p  def flow(self, path, rnd=False): if not path:  return [] fl = [] for p in path: if not rnd: fl.append(p[:-1]) else: pr = list(p[:-1]) random.shuffle(pr) fl.append(tuple(pr)) return fl  def fORx(self, flow, f=0): '''index: f=0, x=1 or x=0, f=1''' def add_empty(): empty = [] for k in graph: for x in graph[k]: z = list(set(x[0].split('|')) - set(list(graph.keys()))) if z: empty.append(z[0]) return empty  if not flow: return []  graph = {} fli = flow[0]  for t in flow[1:]: if f == 0: if fli[1] not in graph: graph[fli[1]] = [] r = [(i, xf) for i,xf in enumerate(graph[fli[1]]) if xf[1] == fli[0]] if r: if t[1] not in r[0][1][0]: x_new = r[0][1][0] + "|" + t[1] if x_new != '': graph[fli[1]][r[0][0]] = (x_new, r[0][1][1]) if not r: if t[1] != '': graph[fli[1]].append((t[1], fli[0]))  if f == 1: if fli[0] not in graph: graph[fli[0]] = [] r = [(i, xf) for i,xf in enumerate(graph[fli[0]]) if xf[1] == fli[1]] if r: if t[0] not in r[0][1][0]: x_new = r[0][1][0] + "|" + t[0] if x_new != '': graph[fli[0]][r[0][0]] = (x_new, r[0][1][1]) if not r: if t[0] != '': graph[fli[0]].append((t[0], fli[1])) fli = t  em = add_empty() if em: graph[em[0]] = [] return graph  def merge(self, g1, g2): def find_index(): for i in range(len(graph[k])): if graph[k][i][1] == x[1]: return i return -1  all_keys = set(list(g1.keys()) + list(g2.keys())) graph = {}  for k in all_keys: if k not in graph:  if k in g1: graph[k] = g1[k] else: graph[k] = g2[k]  if k in g2: for x in g2[k]: ind = find_index() if ind != -1: if x[0] != []: t1 = x[0].split('|') if graph[k][ind] != -1: t2 = graph[k][ind][0].split('|') z = "|".join(set(t1+t2)) xf = [z, graph[k][ind][1]] graph[k][ind] = xf else: graph[k].append(x)  return graph   #--------- main ---------#     if __name__ == "__main__":  g = { "1": [["2", "11"], ["10", "15"]], "2": [["3", "11"], ["9", "12"]],  "3": [["4", "11"], ["2", "13"], ["6", "12"]],  "4": [["5|1", "11"]],  "5": [["6", "11"]],  "6": [["7", "11"]],  "7": [["8", "11"], ["5", "12"]],  "8": [["9", "11"]],  #"9": [['1|5', '11']], '9':[], "10":[["5", "15"]] }  hd = Hd(g) r_ = hd.get_ku(hd.graph) print("Исходный граф: Коэффициент однозначности ku = ", r_[0]) hd.show(hd.graph); print()  epochs = 50 ku_list = [[],[]] gf = [{}, {}]  for i in range(epochs): print("\n_____ЭПОХА = ", i+1) x = random.choice(list(g.keys())); print("начинаем с состояния ", x) #x = '1'  x_list, f_list = hd.get_states(x, [], n=20)  path = hd.get_yfx(f_list, x_list) path_yfx = hd.get_yfx(f_list, x_list, t = False) '''if path_yfx: print("y=f(x) :", *path_yfx) pass'''  print("  Наблюдение") for fl in hd.flow(path, rnd=False): print(*fl)  print("\n  гипотеза 1: ") gn = hd.fORx(hd.flow(path), f=0) hd.show(gn) gf[0] = hd.merge(gf[0], gn) r = hd.get_ku(gf[0]) print("\nКоэффициент однозначности ku = ", r[0]) ku_list[0].append(r[0]) hd.show(gf[0]) print()  print("\n  гипотеза 2: ") gn = hd.fORx(hd.flow(path), f=1) hd.show(gn) gf[1] = hd.merge(gf[1], gn) r = hd.get_ku(gf[1]) print("\nКоэффициент однозначности ku = ", r[0]) ku_list[1].append(r[0]) hd.show(gf[1])  print() fig, ax = plt.subplots() ax.plot([i+1 for i in range(epochs)], ku_list[0], marker="*", color='g') ax.plot([i+1 for i in range(epochs)], ku_list[1], marker="+", color='b') ax.plot([i+1 for i in range(epochs)], [r_[0]]*epochs,  color='r') ax.set_xlabel('эпоха') ax.set_ylabel('коэффициент однозначности') plt.show()