SQL HowTo: обход дерева иерархии «по курсору» через двойную рекурсию

В предыдущих статьях «PostgreSQL Antipatterns: навигация по реестру», «PostgreSQL 13: happy pagination WITH TIES» и «SQL HowTo: курсорный пейджинг с неподходящей сортировкой» я уже рассматривал проблемы навигации по данным, представленных в виде плоского реестра.

Но что если мы хотим выводить данные не простым «бесконечным списком», а в виде иерархической структуры с быстрой навигацией по узлам — например, обширный каталог товаров или меню ресторана, как это делает Presto — наш продукт для автоматизации заведений питания?

Формируем датасет

Для начала сгенерируем наш тестовый иерархичный каталог на 100K позиций:

CREATE TABLE hier(   id  -- PK     integer       PRIMARY KEY , pid -- ссылка на "предка"     integer       REFERENCES hier         ON DELETE CASCADE , ord -- пользовательский порядковый номер внутри раздела     integer );  INSERT INTO hier SELECT   id , nullif((random() * id)::integer, 0) pid , (random() * 1e5)::integer ord FROM   generate_series(1, 1e5) id; -- 100K записей

Из размера уже становится понятно, что решения вроде «Давайте все сразу развернем в нужном порядке как описано тут, а потом спозиционируемся через OFFSET» адекватно работать не будут.

Теперь договоримся, что порядок вывода записей внутри одного раздела, определяемый полем ord, будет уникальным. Для этого нам надо вычистить все дубли пар (pid, ord), как мы делали это в статье «DBA: вычищаем клон-записи из таблицы без PK»:

DELETE FROM   hier WHERE   ctid = ANY(ARRAY(     SELECT       unnest((array_agg(ctid))[2:]) ctids     FROM       hier     GROUP BY       pid, ord     HAVING       count(*) > 1   )); -- теперь никто не мешает индексу по разделу быть уникальным CREATE UNIQUE INDEX ON hier(pid, ord);

Алгоритм обхода

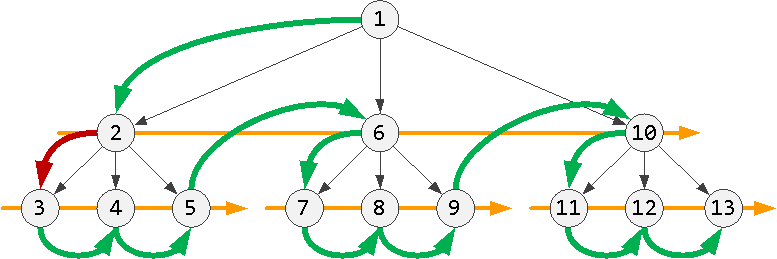
Давайте формализуем описание алгоритма, как он должен набрать N записей для следующей «страницы», начиная с конкретного ключа — пары (pid, ord). Он будет состоять всего из 3 разных вариантов, которые надо проверить последовательно.

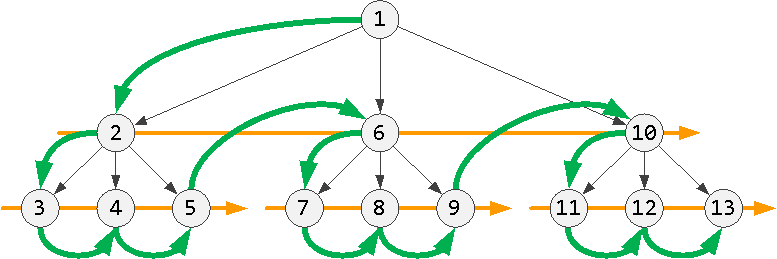
1. Взять первого по порядку потомка на уровень ниже:

   

2. Если такого нет, взять «соседа» на текущем уровне:

   

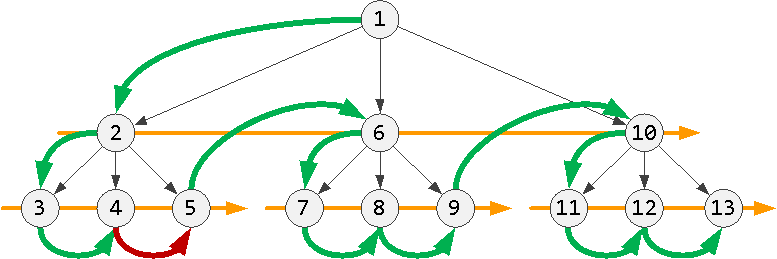
3. Если такого нет, взять «соседа» у ближайшего предка, у которого он есть:

   

Если же ни у одного предка не оказалось «соседа» — все, мы обошли все дерево.

Собираем SQL

1. наш алгоритм итеративно переходит от одной записи к другой — то есть для SQL это будет рекурсивным запросом;

2. паттерн «если такого нет, возьми следующий вариант» легко реализуется с помощью кейса UNION ALL + LIMIT 1 (см. статью);

3. «ближайшего предка с соседом» придется искать тоже рекурсивно;

4. для ограничения количества набираемых N записей разумнее всего использовать обычный счетчик.

Звучит не слишком страшно, но надо учесть, что п.3 разделится еще на два — когда узел находится где-то в глубине дерева, и когда он находится в корне (pid IS NULL):

WITH RECURSIVE T AS(   SELECT     h   -- тут будет лежать сразу цельная запись, чтобы не перечитывать ее повторно   , 0 i -- счетчик найденных записей   FROM     hier h   WHERE     id = 10000 -- последняя прочитанная на предыдущей итерации запись UNION ALL   SELECT     X._h   , i + 1   FROM     T   , LATERAL (       -- первый потомок       (         SELECT           _h         FROM           hier _h         WHERE           pid = (T.h).id         ORDER BY           ord         LIMIT 1       )       UNION ALL       -- ближайший "сосед"       (         SELECT           _h         FROM           hier _h         WHERE           pid = (T.h).pid AND           ord > (T.h).ord         ORDER BY           ord         LIMIT 1       )       UNION ALL       -- ближайший "сосед" ближайшего предка       (         WITH RECURSIVE _T AS(           SELECT             T.h p         -- берем текущую запись в качестве "предка"           , NULL::hier _h -- "соседа" у нее заведомо нет         UNION ALL           SELECT             __h           , (               -- сработает только один из блоков с противоположными условиями               (                 SELECT                   __h                 FROM                   hier __h                 WHERE                   (_T.p).pid IS NOT NULL AND -- мы еще не в корне                   pid = (_T.p).pid AND                   ord > (_T.p).ord                 ORDER BY                   pid, ord -- подгоняем под индекс                 LIMIT 1               )               UNION ALL               (                 SELECT                   __h                 FROM                   hier __h                 WHERE                   (_T.p).pid IS NULL AND     -- уже в корне                   pid IS NULL AND                   ord > (_T.p).ord                 ORDER BY                   pid, ord -- подгоняем под индекс                 LIMIT 1               )               LIMIT 1             )           FROM             _T           INNER JOIN             hier __h               ON __h.id = (_T.p).pid -- рекурсивный обход "вверх" по иерархии         )         SELECT           _h         FROM           _T         WHERE           _h IS DISTINCT FROM NULL         LIMIT 1       )       LIMIT 1     ) X   WHERE     X._h IS DISTINCT FROM NULL AND     i < 20 -- количество записей на странице ) SELECT   (h).*  -- разворачиваем поля записи FROM   T WHERE   i > 0; -- убираем "стартовую" запись

Проверим план запроса на explain.tensor.ru:

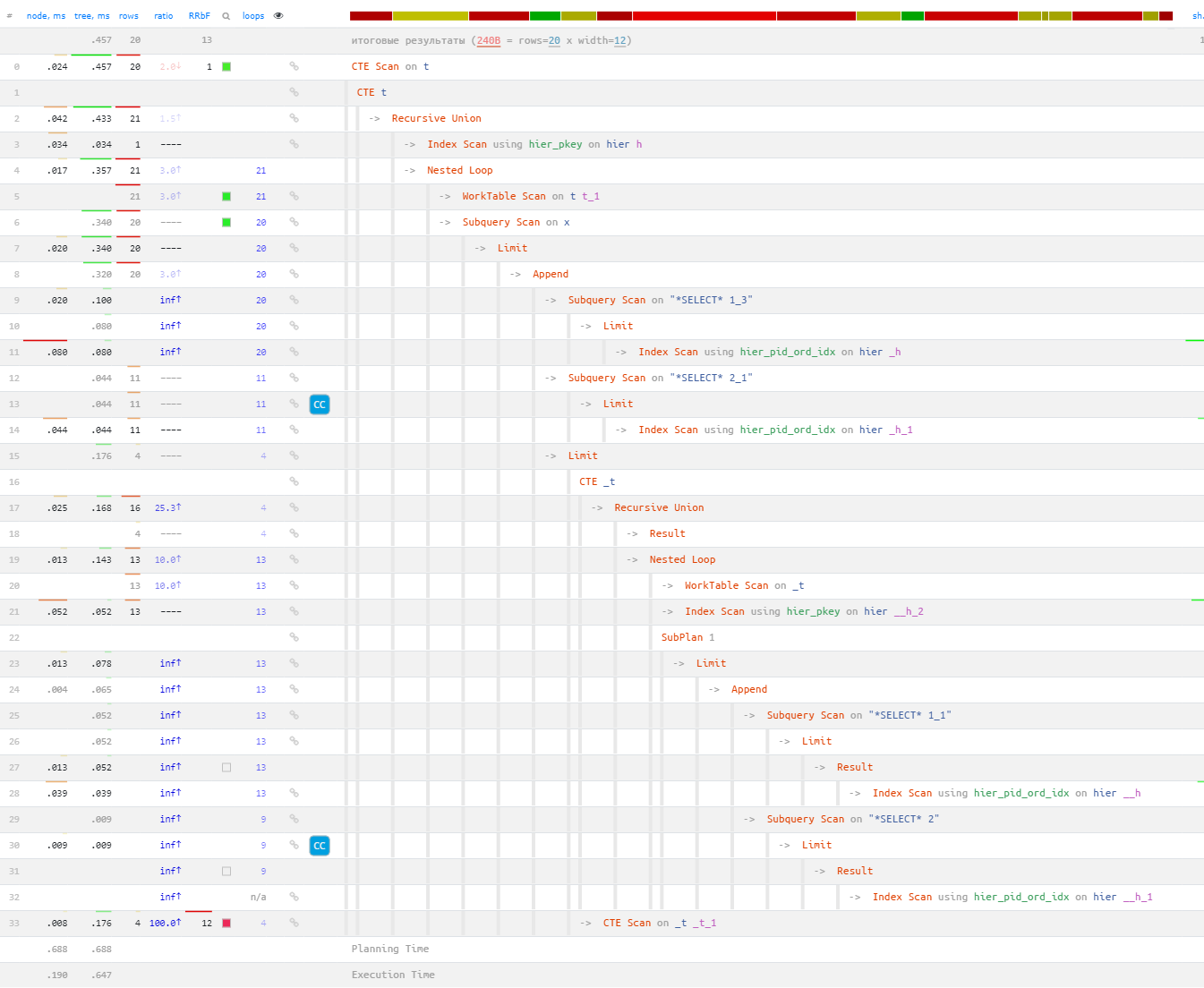
Все выполнение для поиска 20 записей заняло меньше полмиллисекунды! При этом никаких Seq Scan или Sort, все исключительно по индексам (всего 58 обращений):

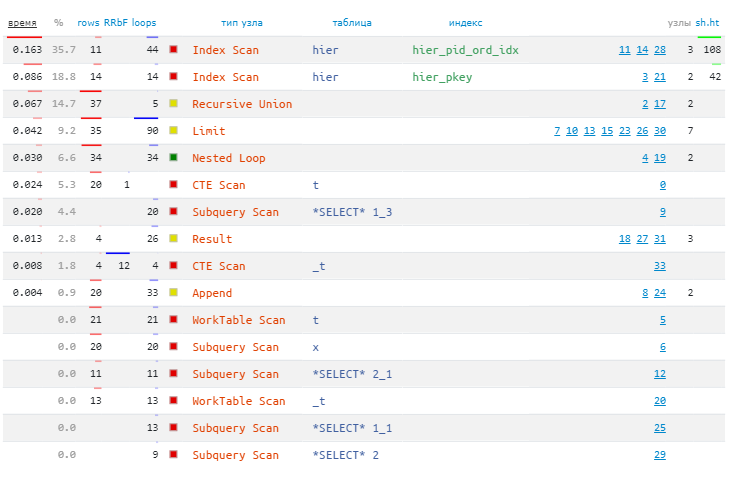
А разве попроще нельзя?..

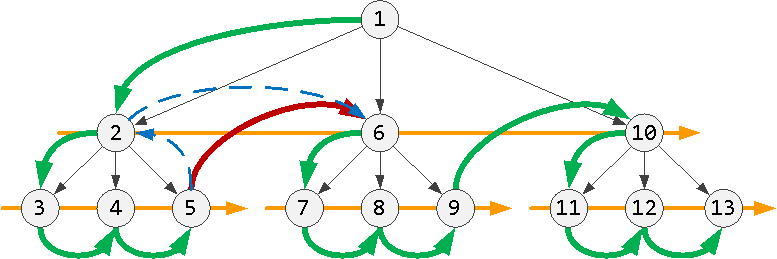
Конечно, можно! Достаточно заметить, что случаи #2 и #3 логически одинаковы — нужно взять ближайшего «соседа» по всей цепочке предков, но начиная с самой же записи. Поэтому второй блок из UNION ALL можно просто убрать — и результат останется ровно тем же самым!

Но вот план — немного ухудшится, и вместо 150 страниц данных для тех же записей придется читать уже 163, поскольку рекурсивный поиск первого предка теперь будет производиться для каждой записи — даже для той, у которой есть «сосед».