Physically-based rendering. Ray marching (часть 2)

Привет, с вами снова Герман и продолжение моей статьи про рендеринг. В первой части, которую вы можете найти по ссылке (link), мы поговорили о трассировке лучей и маршевом методе, а в этой части мы с вами получим изображение мыльного пузыря.

Интерференция света в мыльной пленке

Для того, чтобы мыльный пузырь был реалистичен, мы должны понимать, что радужные пятна на поверхности мыльного пузыря возникают из-за интерференции света. Часть света проходит внутрь пленки, остальная часть отражается, так как толщина пленки непостоянна: при каждом проходе свет смещается на определенное значение, пропорциональное длине волны и зависящее от толщины этой мыльной пленки. Чтобы понять, на какое значение смещается длина волны испускаемого света, рассмотрим небольшую часть мыльной пленки, как показано на рисунке 1.

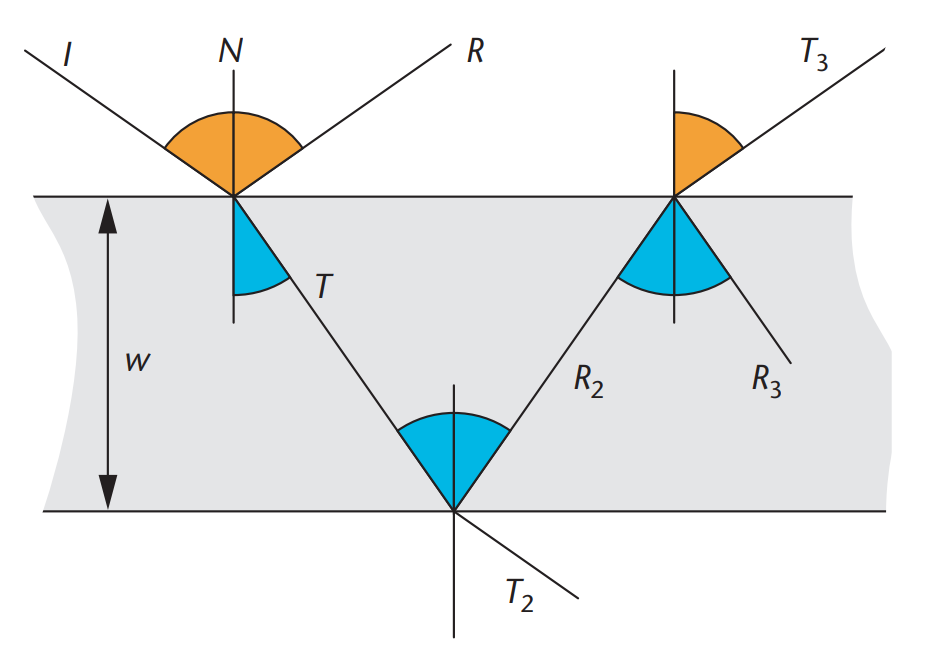
Рис. 1 - Преломление и отражение света в мыльной пленке — Рис. 1 — Преломление и отражение света в мыльной пленке

Луч света из направления падает на верхнюю поверхность. Часть этого света отражается в направлении , в то время как остальная часть проходит дальше в пленку в направлении . На нижнем куске пленки часть света проходит внутрь пузырька в направлении , в то время как остальная часть отражается обратно вверх в направлении . Этот свет попадает на верхнюю часть пленки, где часть отражается обратно в пленку в направлении , остальная часть возвращается в воздух в направлении . Примем во внимание, что есть важное свойство для мыльных пленок, которое я не буду доказывать в этой статье: параллелен направлению . Таким образом, свет, движущийся по , будет взаимодействовать со светом на . Так как свет — это волна, выходная интенсивность будет зависеть от длины волны и фазы каждой составляющей волны.

Давайте предположим, что свет, поступающий вдоль имеет длину волны (измеряется в нанометрах). Пленка имеет толщину , а показатель преломления пленки равен (около 1.4 для мыльных пленок). Угол падения между и нормалью к поверхности равен . Свет, который проходит через пленку и выходит параллельно, будет сдвинут по фазе относительно света, который просто отражается от поверхности. Как мы знаем, разность фаз между этими двумя волнами будет определять, усиливают ли они или гасят друг друга, и полностью это происходит или частично. Наша с вами цель состоит в том, чтобы определить разность фаз между отраженным светом и светом на . Мы имеем два компонента: дополнительное расстояние, пройденное по более длинному пути, и оптический сдвиг фазы на границе раздела. Рассмотрим их по порядку — нам нужно найти общую разницу в расстоянии, пройденном двумя лучами. Если мы разделим расстояние на длину волны, результат покажет нам, какую часть цикла пройдет свет на протяжении всего прохождения. На рисунке 2 вы можете заметить дополнительную точку наряду с точками ,и.

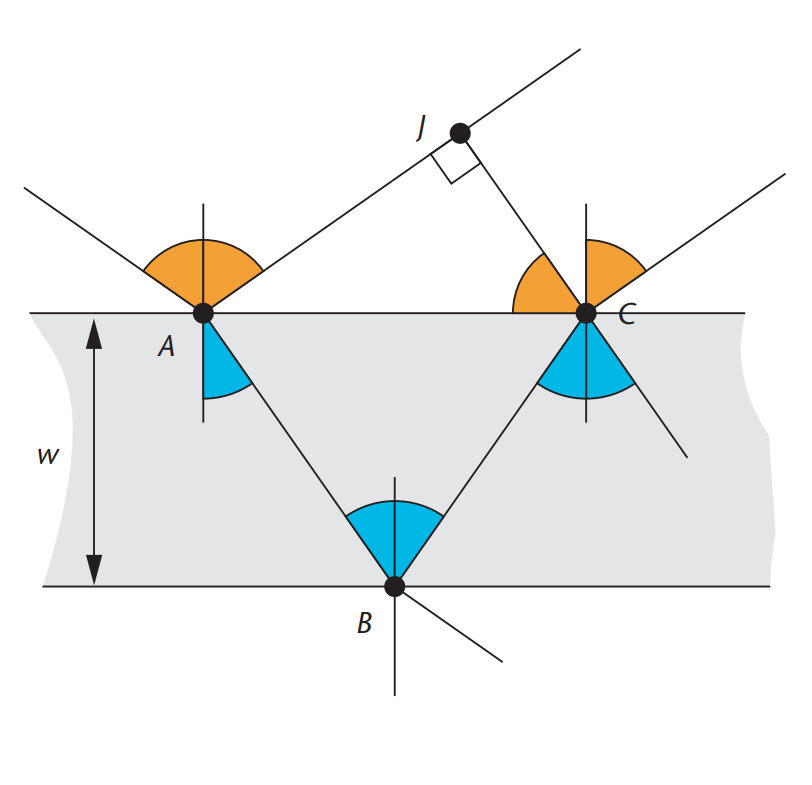
Теперь мы можем говорить о двух параллельных лучах света — один проходит от к , другой от до и затем до . Геометрическая разница в расстоянии составляет . Если мы найдем эту разницу и преобразуем ее в количество радиан, которое она представляет для этой длины волны, мы получим разность фаз и, следовательно, максимальную яркость объединенного света, исходящего от пленки.

Вы скорее всего помните, что свет распространяется медленнее в более плотной, чем воздух, среде, например, в мыльной воде. Поскольку свет движется медленнее, волна проходит большую часть своего периода, проходя через воду, нежели через эквивалентное расстояние по воздуху. Мы моделируем этот эффект, умножая пройденное расстояние на показатель преломления, увеличивающий длину до эквивалентного расстояния, которое волна преодолела бы в воздухе за то же время. Таким образом, эта часть разности фаз составляет $d = \mu(AB + BC) − AJ$ . Тригонометрия позволяет нам определить значение для . Обратившись к рисунку 2, мы видим, что $cos(\theta_t) = \frac{w}{AC}$ и что . Вернемся к первой части и найдем . Поскольку угол $∠ACJ = \theta_i$ мы видим, что $AJ = ACsin(\theta_i)$ . Воспользуемся законом Снеллиуса, чтобы заменить $sin(\theta_i)$ его эквивалентом $\eta sin(\theta_t)$ . Из рисунка 2 понятно, что $tan(\theta_t)$ = , поэтому $AC = 2w tan(\theta_t)$ . Подставляя это значение для в выражение для , которое мы только что получили, и складывая все это вместе, мы находим:

$\begin{equation} d=\frac{2 \eta w}{\cos \theta_{t}}-2 w \tan \theta t \eta \sin \theta t \end{equation}$

Упростим это выражение:

$\begin{equation} \begin{array}{l} d=2 w \eta\left(\frac{1}{\cos \theta_{t}}-\frac{\sin ^{2} \theta_{t}}{\cos \theta_{t}}\right) =\frac{2 w \eta}{\cos \theta_{t}}\left(1-\sin ^{2} \theta_{t}\right)=\frac{2 w \eta}{\cos \theta_{t}} \cos ^{2} \theta_{t} \\ =2 w \eta \cos \theta_{t} \end{array} \end{equation}$

Отлично, мы почти закончили со скучными вычислениями и разобрались с первым членом разности фаз. Второй член — это оптический сдвиг фазы. Оказывается, когда свет переходит из одной среды в среду с более высоким показателем преломления (например, из воздуха в мыльную воду), он претерпевает фазовый сдвиг, равный половине длины его волны (интересно, что этого не происходит на обратном пути). Нам нужно добавить $\lambda / 2$ к разнице, рассчитанной выше, поскольку свет проходит из воздуха в мыло в точке . Это даст нам эффективную длину оптического пути (EOPL):

$\begin{equation} EOPL = d + \lambda / 2 = 2 w \eta \cos \theta_{t} + \lambda / 2 \end{equation}$

Теперь у нас есть понимание, как должен вычисляться интерференционный свет в мыльной пленке. Для того, чтобы понять, как преобразовывать длину волны в RGB цвета, я советую ознакомиться с этой статьей.

Если вы все сделали правильно, должно получиться что-то подобное (рисунок 3).

Рис. 3 - pbr рендер мыльного пузыря — Рис. 3 — pbr рендер мыльного пузыря

Возможно кому-то раздел об интерференции показался скучным, и возникло желание получить похожий результат без особых усилий и размышлений, поэтому попробуем другой способ получить реалистичный результат с помощью случайности и броуновского движения.

Деформация или искажение цвета

Деформация или искажение цвета — очень распространенный метод в компьютерной графике для создания процедурных текстур и геометрии. Он часто используется, чтобы сжать объект, растянуть его, скрутить, согнуть, сделать его толще или применить любую деформацию, которую захотите . Это работает до тех пор, пока базовый цветовой узор или геометрия определяются как функция пространства. Мы с вами разберем очень частный случай деформации — искажение на основе шума или функцию шума. Такой способ используется с 1984 года, когда сам Кен Перлин создал свою первую процедурную текстуру мрамора.

Рис. 4 - Шум Перлина для процедурной генерации текстуры мрамора. — Рис. 4 — Шум Перлина для процедурной генерации текстуры мрамора.

Предположим, что у нас есть некоторая геометрия или изображение, определенное как функция расстояния (SDF). Для поверхности, как это было показано ранее, это будет функция вида , а для изображения — (координаты пикселя). Мы можем записать оба случая более компактно как , где — это положение в пространстве, для которого можно оценить объемную плотность, определяющую нашу поверхность или цвет изображения. Деформация же означает, что мы искажаем область с помощью другой функции перед тем, как вычислить . По сути, мы заменяем на . Функция может быть чем угодно, но часто мы хотим исказить образ в небольшой степени по отношению к его обычному поведению. Тогда имеет смысл представить как тождество, суммированное с небольшим произвольным искажением или, другими словами, , что означает, что мы будем вычислять

Эта техника действительно хорошая и позволяет формировать яблоки, здания, животных или любые другие вещи, которые вы можете себе представить. Далее будем работать с паттернами на основе (функции дробного броуновского движения), как для , так и для . Это позволит нам моделировать паттерны, похожие на радужные пленки на поверхности мыльных пузырей без расчета интерференции.

Само по себе дробное броуновское движение представляет собой простую сумму волн с увеличивающимися частотами и уменьшающимися амплитудами. Так как в GLSL нет функции для генерации случайных чисел, мы напишем свою:

const mat2 m = mat2( 0.80,  0.60, -0.60,  0.80 );  float noise( in vec2 p ) { return sin(p.x)*sin(p.y); }  float fbm( vec2 p ) {     float f = 0.0;     f += 0.500000*(0.5+0.5*noise( p )); p = m*p*2.02;     f += 0.250000*(0.5+0.5*noise( p )); p = m*p*2.03;     f += 0.125000*(0.5+0.5*noise( p )); p = m*p*2.01;     f += 0.062500*(0.5+0.5*noise( p )); p = m*p*2.04;     f += 0.031250*(0.5+0.5*noise( p )); p = m*p*2.01;     f += 0.015625*(0.5+0.5*noise( p ));     return f/0.96875; }

Мне, например, понадобилось 15 минут на то, чтобы подобрать паттерн, искажающий цвета таким образом, чтобы это было похоже на интерференцию в мыльной пленке. Вы можете поиграть с параметрами так, чтобы результат был лучше:

float pattern( in vec2 p, out vec2 q, out vec2 r ) {     q.x = fbm( p + vec2(0.0,0.1 * iTime) );     q.y = fbm( p + vec2(5.2,1.3) );      r.x = fbm( p + 4.0*q + vec2(100.7 + 0.1 * iTime,91.2) );     r.y = fbm( p + 4.0*q + vec2(90.3,2.8 + 0.1 * iTime) );      return fbm(vec2(fbm( p * p + 10.0*r + fbm(5.0 * p + q)), fbm(100.0 * p * p * q))); }

В итоге мы с вами получили достаточно реалистичный рендер мыльного пузыря без серьезных размышлений (рисунок 5).

Рис. 5 - pbr рендер мыльного пузыря без сложных физических вычислений — Рис. 5 — pbr рендер мыльного пузыря без сложных физических вычислений

Antialiasing

В трассировке лучей возникает достаточно часто возникает такая проблема, как aliasing. Заключается она в эффекте ступенчатости, который проявляется на границах поверхностей. Эффект возникает из-за недостаточной точности расчета цвета пикселя по одному лучу. Если присмотреться к границе пузыря на рисунке 6, то мы увидим лесенку:

Рис. 6 - Aliasing при рендере мыльного пузыря — Рис. 6 — Aliasing при рендере мыльного пузыря

Чтобы избавиться от этой проблемы, мы будем выпускать по 4 луча на каждый пиксель с небольшим смещением и для каждого луча получать цвет объекта. После этого мы усредним цвет в пикселе.

    <...>     vec3 rayDir1 = getRayDirection(uv, cameraPos, lookAt);     vec3 rayDir2 = getRayDirection(uv, cameraPos, lookAt + vec3(0.01, 0.0, 0.0));     vec3 rayDir3 = getRayDirection(uv, cameraPos, lookAt + vec3(0.0, 0.01, 0.0));     vec3 rayDir4 = getRayDirection(uv, cameraPos, lookAt + vec3(0.0, 0.0, 0.01));     vec4 col1 = render(cameraPos, rayDir1);      vec4 col2 = render(cameraPos, rayDir2);     vec4 col3 = render(cameraPos, rayDir3);     vec4 col4 = render(cameraPos, rayDir4);          vec4 col = 0.25 * (col1 + col2 + col3 + col4);     // Output to screen     fragColor = col;     <...>

Рис. 6 - Рендер мыльного пузыря с использованием antialiasing — Рис. 6 — Рендер мыльного пузыря с использованием antialiasing

На рисунке 6 можно заметить, что граница стала плавнее, но FPS упал в 4 раза, т.к. сейчас нам приходится рендерить сцену 4 раза для получения одного кадра. Метод достаточно затратный, но эта красота того стоит!

На этом вторая часть статьи про pbr rendering подошла к концу. Благодарю всех, кто остался со мной до конца, оставляйте свои вопросы в комментариях, буду рад ответить.

Исходный код шейдера доступен по ссылке.

ссылка на оригинал статьи https://habr.com/ru/company/constanta/blog/684016/

Physically-based rendering. Ray marching (часть 2)

Интерференция света в мыльной пленке

Деформация или искажение цвета

Antialiasing

Комментарии

Добавить комментарий Отменить ответ