Уроки компьютерного зрения на Python + OpenCV с самых азов. Часть 8

На прошлом уроке мы углубились в изучение контуров. В частности, научились работать со структурой, которую возвращает функция выделения контуров, научились аппроксимировать и обходить контур, научились программировать кое-какие геометрические операции, чтобы создать инвариантное описание объекта. Напомню, как это мы сделали: нашли контур объекта, аппроксимировали его, обошли этот контур, вычислили косинусы углов между гранями аппроксимированного контура.

Сегодня продолжим тему прошлого урока. Вычислим инвариантный вектор новым методом: через отношения длин сторон. Мы начнем обход так же с самой удаленной от центра точки, только будем брать стороны, а не углы межу сторонами. И первая сторона это та, что прилегает к первой точке. То есть она соединяет первую точку и следующую за ней по часовой стрелке. И все эти длины сторон мы разделим на самую длинную сторону. Хотя нет, сделам лучше. Сделаем минимакс нормализацию: вычтем из длины стороны минимум и разделим на разницу между минимумом и максимумом. У нас будет вектор чисел от 0 до 1.

И так, займемся кодингом. Сначала напишем цикл, создающий исходный масcив:

lengths=[] for i in range(size-1):     lengths.append(get_length(polar_coordinates[i],polar_coordinates[i+1])) lengths.append(get_length(polar_coordinates[size-1],polar_coordinates[0])) print(get_normalize_normalize(lengths))

Функция вычисления длины стороны (она просто извекает из структуры, где у нас все храниться, координаты и считает эвклидово расстояние):

#Эвклидово расстояние между двумя элементами def get_length(item1, item2):     _, point1 = item1     _, point2 = item2     x1, y1 = point1     x2, y2 = point2     dx=x1-x2     dy=y1-y2     r=math.sqrt(dx*dx+dy*dy)     return r

Ну и нормализация, конвертим полученный список в numpy массив и делаем минимакс нормализацию:

def get_normalized_vector(list):     arr=np.array(list)     return (arr-arr.min())/(arr.max()-arr.min())

Поехали смотреть, что получилось.

Первый пример:

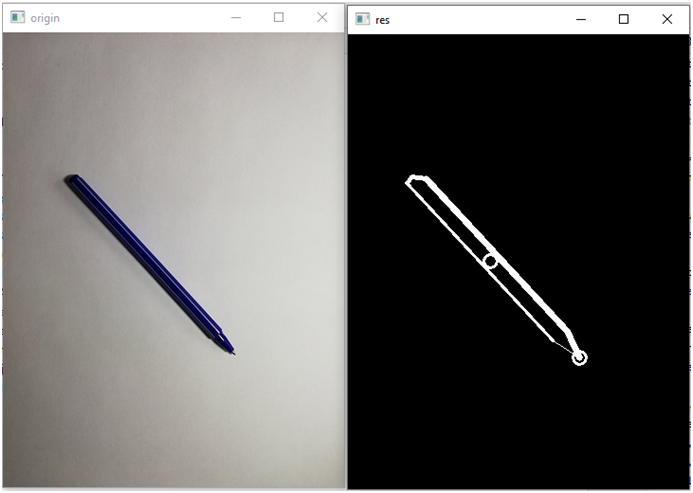
Вектор: [0.11331868 1.         0.         0.02997931 0.96756226 0.1022278 ]

 

Второй пример:

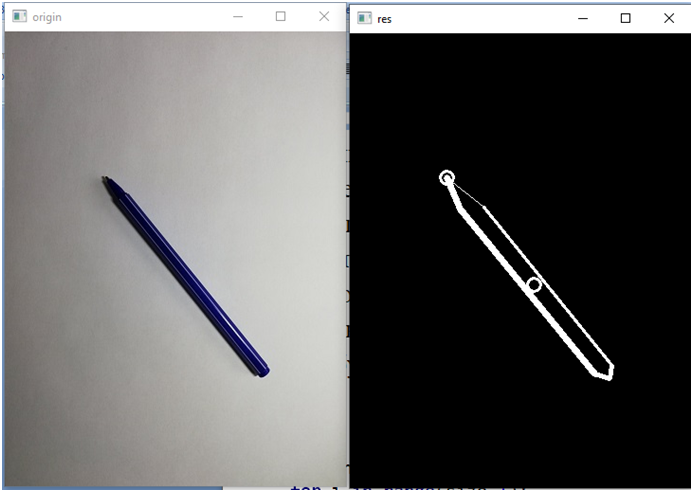
Вектор: [0.16953268 0.9532099  0.         0.01245409 1.         0.10313678]

 

Как видим, векторы действительно оказались близкие. Причем, в отличие от прошлого варианта, у нас остаются стабильными все элементы вектора.

Вообще, по-хорошему, конечно надо бы провести исследование: проанализировать множество изображений, сравнить, насколько расходятся векторы инвариантных описаний при том или ином методе расчета. Да и программа нуждается в рефакторинге. Но это уже выходит за рамки уроков. Поэтому я привожу полный код примеров как есть, и мы двигаемся дальше:

import cv2 import numpy as np import math import os img = cv2.imread("Samples/1.jpg") gray = cv2.cvtColor(img, cv2.COLOR_BGR2GRAY) thresh = 100  def custom_sort(countour):     return -countour.shape[0]  def polar_sort(item):     return item[0][0]  def get_normalized_vector(list):     arr=np.array(list)     return (arr-arr.min())/(arr.max()-arr.min())  #Эвклидово расстояние между двумя элементами def get_length(item1, item2):     _, point1 = item1     _, point2 = item2     x1, y1 = point1     x2, y2 = point2     dx=x1-x2     dy=y1-y2     r=math.sqrt(dx*dx+dy*dy)     return r  def get_cos_edges(edges):     dx1, dy1, dx2, dy2=edges     r1 = math.sqrt(dx1 * dx1 + dy1 * dy1)     r2 = math.sqrt(dx2 * dx2 + dy2 * dy2)     return (dx1*dx2+dy1*dy2)/r1/r2  def get_polar_coordinates(x0,y0,x,y,xc,yc):     #Первая координата в полярных координатах - радиус     dx=xc-x     dy=yc-y     r=math.sqrt(dx*dx+dy*dy)      #Вторая координата в полярных координатах - узел, вычислим относительно начальной точки     dx0=xc-x0     dy0=yc-y0     r0 = math.sqrt(dx0 * dx0 + dy0 * dy0)     scal_mul=dx0*dx+dy0*dy     cos_angle=scal_mul/r/r0     sgn=dx0*dy-dx*dy0 #опредедляем, в какую сторону повернут вектор     if cos_angle>1:         if cos_angle>1.0001:             raise Exception("Что-то пошло не так")         cos_angle=1     angle=math.acos(cos_angle)     if sgn<0:         angle=2*math.pi-angle     return angle,r  def get_coords(item1, item2, item3):     _, point1 = item1     _, point2 = item2     _, point3 = item3     x1, y1 = point1     x2, y2 = point2     x3, y3 = point3     dx1=x1-x2     dy1=y1-y2     dx2=x3-x2     dy2=y3-y2     return dx1,dy1,dx2,dy2  #get threshold image ret,thresh_img = cv2.threshold(gray, thresh, 255, cv2.THRESH_BINARY)  # find contours without approx contours,_ = cv2.findContours(thresh_img,cv2.RETR_TREE,cv2.CHAIN_APPROX_NONE) contours=list(contours) contours.sort(key=custom_sort) sel_countour=contours[1]  # calc arclentgh arclen = cv2.arcLength(sel_countour, True)  # do approx eps = 0.01 epsilon = arclen * eps approx = cv2.approxPolyDP(sel_countour, epsilon, True)  sum_x=0.0 sum_y=0.0 for point in approx:     x = float(point[0][0])     y = float(point[0][1])     sum_x+=x     sum_y+=y xc=sum_x/float(len((approx))) yc=sum_y/float(len((approx)))  max=0 beg_point=-1 for i in range(0,len(approx)):     point=approx[i]     x = float(point[0][0])     y = float(point[0][1])     dx=x-xc     dy=y-yc     r=math.sqrt(dx*dx+dy*dy)     if r>max:         max=r         beg_point=i  polar_coordinates=[] x0=approx[beg_point][0][0] y0=approx[beg_point][0][1]  for point in approx:     x = int(point[0][0])     y = int(point[0][1])     angle,r=get_polar_coordinates(x0,y0,x,y,xc,yc)     polar_coordinates.append(((angle,r),(x,y)))  polar_coordinates.sort(key=polar_sort)  img_contours = np.uint8(np.zeros((img.shape[0],img.shape[1]))) size=len(polar_coordinates) for i in range(1,size):     _ , point1=polar_coordinates[i-1]     _, point2 = polar_coordinates[i]     x1,y1=point1     x2,y2=point2     cv2.line(img_contours, (x1, y1), (x2, y2), 255, thickness=i) _ , point1=polar_coordinates[size-1] _, point2 = polar_coordinates[0] x1,y1=point1 x2,y2=point2 cv2.line(img_contours, (x1, y1), (x2, y2), 255, thickness=size)  cv2.circle(img_contours, (int(xc), int(yc)), 7, (255,255,255), 2)  coses=[] coses.append(get_cos_edges(get_coords(polar_coordinates[size-1],polar_coordinates[0],polar_coordinates[1]))) for i in range(1,size-1):     coses.append(get_cos_edges(get_coords(polar_coordinates[i-1], polar_coordinates[i],polar_coordinates[i+1]))) coses.append(get_cos_edges(get_coords(polar_coordinates[size-2], polar_coordinates[size-1],polar_coordinates[0]))) print(coses)  lengths=[] for i in range(size-1):     lengths.append(get_length(polar_coordinates[i],polar_coordinates[i+1])) lengths.append(get_length(polar_coordinates[size-1],polar_coordinates[0])) print(get_normalized_vector(lengths))    point=approx[beg_point] x = float(point[0][0]) y = float(point[0][1]) cv2.circle(img_contours, (int(x), int(y)), 7, (255,255,255), 2)  cv2.imshow('origin', img) # выводим итоговое изображение в окно cv2.imshow('res', img_contours) # выводим итоговое изображение в окно  cv2.waitKey() cv2.destroyAllWindows()

Наш следующий шаг в освоении OpenCV – это поиск предмета на изображении. Искать мы будет все ту же ручку, но теперь на изображении у нас будут другие предметы:

Здесь мы точно так же выделим контуры на изображении, а потом каждый из контуров будем проверять на соответствии заданному шаблону – шесть граней и вектор инвариантного описания близок к исходному. Насколько близок? Это определим эмпирическим путем, подбирая порог.

И так, вот программа:

import cv2 import numpy as np import math  template_vector=np.array([0.16953268, 0.9532099, 0, 0.01245409, 1, 0.10313678]) distance_thresh=0.1  img = cv2.imread("Samples/objects.jpg") gray = cv2.cvtColor(img, cv2.COLOR_BGR2GRAY) thresh = 100  def polar_sort(item):     return item[0][0]  def get_normalized_vector(list):     arr=np.array(list)     return (arr-arr.min())/(arr.max()-arr.min())  #Эвклидово расстояние между двумя элементами def get_length(item1, item2):     _, point1 = item1     _, point2 = item2     x1, y1 = point1     x2, y2 = point2     dx=x1-x2     dy=y1-y2     r=math.sqrt(dx*dx+dy*dy)     return r  def get_polar_coordinates(x0,y0,x,y,xc,yc):     #Первая координата в полярных координатах - радиус     dx=xc-x     dy=yc-y     r=math.sqrt(dx*dx+dy*dy)      #Вторая координата в полярных координатах - узел, вычислим относительно начальной точки     dx0=xc-x0     dy0=yc-y0     r0 = math.sqrt(dx0 * dx0 + dy0 * dy0)     scal_mul=dx0*dx+dy0*dy     cos_angle=scal_mul/r/r0     sgn=dx0*dy-dx*dy0 #опредедляем, в какую сторону повернут вектор     if cos_angle>1:         if cos_angle>1.0001:             raise Exception("Что-то пошло не так")         cos_angle=1     angle=math.acos(cos_angle)     if sgn<0:         angle=2*math.pi-angle     return angle,r   #get threshold image ret,thresh_img = cv2.threshold(gray, thresh, 255, cv2.THRESH_BINARY)  # find contours without approx contours,_ = cv2.findContours(thresh_img,cv2.RETR_TREE,cv2.CHAIN_APPROX_NONE) for sel_countour in contours:     # calc arclentgh     arclen = cv2.arcLength(sel_countour, True)      # do approx     eps = 0.01     epsilon = arclen * eps     approx = cv2.approxPolyDP(sel_countour, epsilon, True)      #Обрабатываем только контуры длиной 6 углов     if len(approx)==6:          # вычислим центр тяжести контура         sum_x = 0.0         sum_y = 0.0         for point in approx:             x = float(point[0][0])             y = float(point[0][1])             sum_x += x             sum_y += y         xc = sum_x / float(len((approx)))         yc = sum_y / float(len((approx)))          #найдем начальную точку         max = 0         beg_point = -1         for i in range(0, len(approx)):             point = approx[i]             x = float(point[0][0])             y = float(point[0][1])             dx = x - xc             dy = y - yc             r = math.sqrt(dx * dx + dy * dy)             if r > max:                 max = r                 beg_point = i          #Вычислми полярные координаты         polar_coordinates=[]         x0=approx[beg_point][0][0]         y0=approx[beg_point][0][1]         for point in approx:             x = int(point[0][0])             y = int(point[0][1])             angle, r = get_polar_coordinates(x0, y0, x, y, xc, yc)             polar_coordinates.append(((angle, r), (x, y)))          #Создадим вектор описание         polar_coordinates.sort(key=polar_sort)         size = len(polar_coordinates)         lengths = []         for i in range(size - 1):             lengths.append(get_length(polar_coordinates[i], polar_coordinates[i + 1]))         lengths.append(get_length(polar_coordinates[size - 1], polar_coordinates[0]))         descr=get_normalized_vector(lengths)          #Вычислим эвклидово расстояние         square = np.square(descr - template_vector)         sum_square = np.sum(square)         distance = np.sqrt(sum_square)         if distance<distance_thresh:             for i in range(1, size):                 _, point1 = polar_coordinates[i - 1]                 _, point2 = polar_coordinates[i]                 x1, y1 = point1                 x2, y2 = point2                 cv2.line(img, (x1, y1), (x2, y2), (0,0,255), thickness=4)             _, point1 = polar_coordinates[size - 1]             _, point2 = polar_coordinates[0]             x1, y1 = point1             x2, y2 = point2             cv2.line(img, (x1, y1), (x2, y2), (0,0,255), thickness=size)   cv2.imshow('origin', img) # выводим итоговое изображение в окно  cv2.waitKey() cv2.destroyAllWindows()

Порог подобран 0.1, шаблон – вектор ко второй картинке, где искомый объект повернут в другую сторону, чем тот, что на картинке:

template_vector=np.array([0.16953268, 0.9532099, 0, 0.01245409, 1, 0.10313678]) distance_thresh=0.1

И вот что у нас получилось:

Найден всего один объект. Если порог увеличить до 0.4, то будет найдет и второй объект, но еще несколько «левых» объектов:

Избавить мы можем от них, просто введя критерий размера (не имеет смысл рассматривать слишком малые объекты):

… for sel_countour in contours:     # calc arclentgh     arclen = cv2.arcLength(sel_countour, True)     if arclen<20:         continue …

И вот что мы получим теперь:

Но кто сказал, что надо вообще аппроксимировать контур и считать углы? Мы можем просто обойти контур по кругу, который разделим на определенное кол-во секторов:

count=100 full_angle=2*math.pi i=1 end_angle = float(i) * full_angle / float(count) summ=0.0 count_angles=0.0 signature=[] for item_coord in polar_coord:     angle,r=item_coord     if angle>end_angle:         signature.append((angle,summ/count_angles))         i+=1         end_angle = float(i) * full_angle / float(count)         summ=0         count_angles=0     summ+=r     count_angles+=1 signature.append((angle,summ/count_angles)) print(signature)

Для того, чтобы проверить правильность  формирования сигнатуры, переведем ее опять в декартовы координаты и отобразим. Функция перевода полярных координат в декартовы:

def polar_to_decart(angle,r):     x=math.sin(angle)*r     y=math.cos(angle)*r     return x,y

И вот таким образом мы отобразим сигнатуру:

img_contours = np.zeros((img.shape[0],img.shape[1],3), np.uint8) # np.uint8(np.zeros((img.shape[0],img.shape[1]))) cv2.drawContours(img_contours, [sel_countour], -1, (255,0,0), 1)  for i in range(1,len(signature)):     angle1,r1=signature[i-1]     angle2,r2=signature[i]     x1, y1=polar_to_decart(angle1,r1)     x2, y2 = polar_to_decart(angle2, r2)     cv2.line(img_contours, (int(x1+xc), int(y1+yc)), (int(x2+xc), int(y2+yc)), (0,0,255), thickness=1) angle1,r1=signature[len(signature)-1] angle2,r2=signature[0] x1, y1=polar_to_decart(angle1,r1) x2, y2 = polar_to_decart(angle2, r2) cv2.line(img_contours, (int(x1+xc), int(y1+yc)), (int(x2+xc), int(y2+yc)), (0,0,255), thickness=1)

Да, я специально не стал делать поправку на угол, чтобы совмещать контуры, пусть красный контур (сигнатура) будет повернут, чтобы было лучше видно:

Можно отобразить эту сигнатуру на графике:

x=[] y=[] for item in signature:     angle,r=item     x.append(angle)     y.append(r)  plt.plot(x,y) plt.show()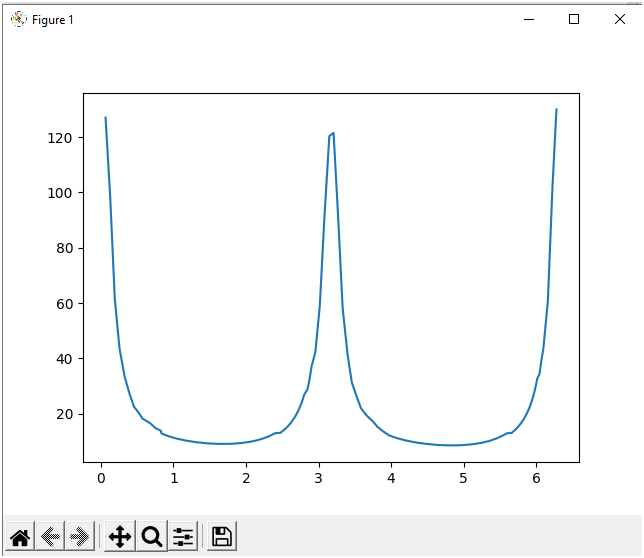

Заметим, что неважно, какой угол поворота, графики будут выглядеть одинаково:

Ну, или почти одинаково:

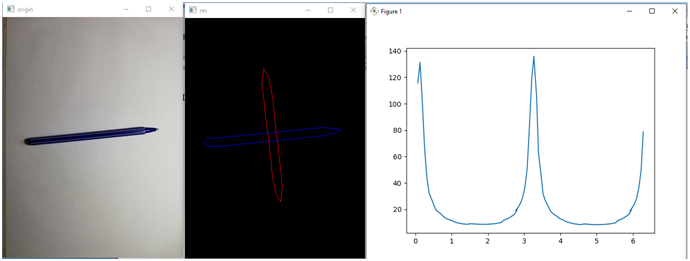
Сравнить мы его сможет так же, как и вектора. Тем более, что теперь у нас контур приведен к единоразмерной сигнатуре.

Попробуем другой предмет:

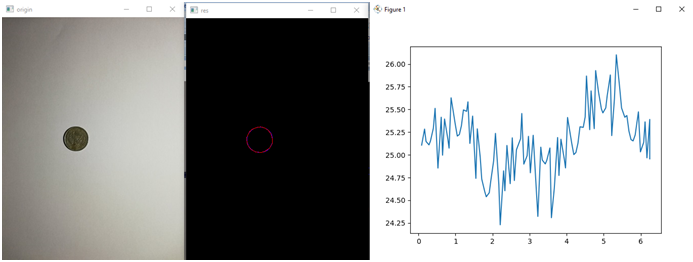
Как видим, в случае круглого предмета получился шум вокруг определенного уровня — радиуса этого круга. В идеале должна, конечно, получиться прямая, но ничего в этом мире нет идеального.  

Еще один предмет:

Еще сигнатуру можно нормировать, тогда мы получим инвариантный к размеру вектор. В прошлый раз мы использовали минимакс, но есть и другие способы, например, можно разделить на радиус или делить разницу между текущим и средним значением на среднеквадратическое отклонение. Но обсуждение способов нормирования уже выходит за рамки статьи.

В заключении полный текст программы.

Файл SignLib.py:

import math   def custom_sort(countour):     return -countour.shape[0]  def get_center(countour):     # вычислим центр тяжести контура     sum_x = 0.0     sum_y = 0.0     for point in countour:         x = float(point[0][0])         y = float(point[0][1])         sum_x += x         sum_y += y     xc = sum_x / float(len((countour)))     yc = sum_y / float(len((countour)))     return xc,yc  def get_beg_point(countour,xc,yc):     max = 0     beg_point = -1     for i in range(0, len(countour)):         point = countour[i]         x = float(point[0][0])         y = float(point[0][1])         dx = x - xc         dy = y - yc         r = math.sqrt(dx * dx + dy * dy)         if r > max:             max = r             beg_point = i         return beg_point  def get_polar_coordinates(x0,y0,x,y,xc,yc):     #Первая координата в полярных координатах - радиус     dx=xc-x     dy=yc-y     r=math.sqrt(dx*dx+dy*dy)      #Вторая координата в полярных координатах - узел, вычислим относительно начальной точки     dx0=xc-x0     dy0=yc-y0     r0 = math.sqrt(dx0 * dx0 + dy0 * dy0)     scal_mul=dx0*dx+dy0*dy     cos_angle=scal_mul/r/r0     sgn=dx0*dy-dx*dy0 #опредедляем, в какую сторону повернут вектор     if cos_angle>1:         if cos_angle>1.0001:             raise Exception("Что-то пошло не так")         cos_angle=1     angle=math.acos(cos_angle)     if sgn<0:         angle=2*math.pi-angle     return angle,r  def polar_to_decart(angle,r):     x=math.sin(angle)*r     y=math.cos(angle)*r     return x,y  def polar_sort(item):     return item[0]  def get_polar_coordinates_list(countour,xc,yc,beg_point):     polar_coordinates = []     x0 = countour[beg_point][0][0]     y0 = countour[beg_point][0][1]     for point in countour:         x = int(point[0][0])         y = int(point[0][1])         angle, r = get_polar_coordinates(x0, y0, x, y, xc, yc)         polar_coordinates.append((angle, r))      # Создадим вектор описание     polar_coordinates.sort(key=polar_sort)      return polar_coordinates

 Основной файл программы:

import math import matplotlib.pyplot as plt import cv2 import numpy as np  from SignLib import custom_sort, get_center, get_beg_point, get_polar_coordinates_list, polar_to_decart  img = cv2.imread("Samples/battery.jpg") gray = cv2.cvtColor(img, cv2.COLOR_BGR2GRAY) thresh = 100  #get threshold image ret,thresh_img = cv2.threshold(gray, thresh, 255, cv2.THRESH_BINARY)  # find contours without approx contours,_ = cv2.findContours(thresh_img,cv2.RETR_TREE,cv2.CHAIN_APPROX_NONE) contours=list(contours) contours.sort(key=custom_sort) sel_countour=contours[1] xc,yc=get_center(sel_countour) beg_point=get_beg_point(sel_countour,xc,yc) polar_coord=get_polar_coordinates_list(sel_countour,xc,yc,beg_point) count=100 full_angle=2*math.pi i=1 end_angle = float(i) * full_angle / float(count) summ=0.0 count_angles=0.0 signature=[] for item_coord in polar_coord:     angle,r=item_coord     if angle>end_angle:         signature.append((angle,summ/count_angles))         i+=1         end_angle = float(i) * full_angle / float(count)         summ=0         count_angles=0     summ+=r     count_angles+=1 signature.append((angle,summ/count_angles)) print(signature)  img_contours = np.zeros((img.shape[0],img.shape[1],3), np.uint8) # np.uint8(np.zeros((img.shape[0],img.shape[1]))) cv2.drawContours(img_contours, [sel_countour], -1, (255,0,0), 1)  for i in range(1,len(signature)):     angle1,r1=signature[i-1]     angle2,r2=signature[i]     x1, y1=polar_to_decart(angle1,r1)     x2, y2 = polar_to_decart(angle2, r2)     cv2.line(img_contours, (int(x1+xc), int(y1+yc)), (int(x2+xc), int(y2+yc)), (0,0,255), thickness=1) angle1,r1=signature[len(signature)-1] angle2,r2=signature[0] x1, y1=polar_to_decart(angle1,r1) x2, y2 = polar_to_decart(angle2, r2) cv2.line(img_contours, (int(x1+xc), int(y1+yc)), (int(x2+xc), int(y2+yc)), (0,0,255), thickness=1)  cv2.imshow('origin', img) # выводим итоговое изображение в окно cv2.imshow('res', img_contours) # выводим итоговое изображение в окно  x=[] y=[] for item in signature:     angle,r=item     x.append(angle)     y.append(r)  plt.plot(x,y) plt.show()  cv2.waitKey() cv2.destroyAllWindows()