SavePearlHarbor

Проверка автокорреляции с использованием критерия Дарбина-Уотсона средствами Python

—

от автора

admin

ПОСТАНОВКА ЗАДАЧИ

Критерий Дарбина-Уотсона (Durbin–Watson statistic) — один из самых распространенных критериев для проверки автокорреляции.

Данный критерий входит в стандартный инструментарий python:

К сожалению, стандартные инструменты python не позволяют получить табличные значения статистики критерия Дарбина-Уотсона, нам предлагается воспользоваться методом грубой оценки: считается, что при расчетном значении статистики критерия в интервале [1; 2] автокорреляция отсутствует (см. https://en.wikipedia.org/wiki/Durbin–Watson_statistic). Однако, для качественного статистического анализа такой подход неприемлем.

Представляет интерес реализовать в полной мере критерий Дарбина-Уотсона средствами python, добавив этот важный критерий в инструментарий специалиста DataScience.

В данном обзоре мы коснемся только собственно критерия Дарбина-Уотсона и его применения для выявления автокорреляции. Особенности построения регрессионных моделей и прогнозирования в условиях автокорреляции (двухшаговый метод наименьших квадратов и пр.) мы рассматривать не будем.

Применение пользовательских функций

Как и в предыдущем обзоре, здесь будут использованы несколько пользовательских функций для решения разнообразных задач. Все эти функции созданы для облегчения работы и уменьшения размера программного кода. Данные функции загружается из пользовательского модуля my_module__stat.py, который доступен в моем репозитории на GitHub (https://github.com/AANazarov/MyModulePython).

Вот перечень данных функций:

  • graph_plot_sns_np — функция строит линейный график средствами seaborn;

  • graph_regression_plot_sns — функция строит график регрессионной модели и график остатков средствами seaborn;

  • regression_error_metrics — функция возвращает ошибки аппроксимации регрессионной модели;

  • graph_hist_boxplot_probplot_sns — функция позволяет визуализировать исходные данные для одной переменной путем одновременного построения гистограммы, коробчатой диаграммы и вероятностного графика средствами seaborn; имеется возможность выбирать, какие графики строить (h — hist, b — boxplot, p — probplot);

  • norm_distr_check — проверка нормальности распределения исходных данных с использованием набора из нескольких статистических тестов.

  • Goldfeld_Quandt_test, Breush_Pagan_test, White_test — проверка гетероскедастичности с использование тестов Голдфелда-Квандта, Бриша-Пэгана и Уайта соответственно;

  • graph_regression_pair_predict_plot_sns — прогнозирование: построение графика регрессионной модели (с доверительными интервалами) и вывод расчетной таблицы с данными для заданной области значений X.

В процессе данного обзора мы создаем пользовательскую функцию Durbin_Watson_test, которая проверяет гипотезу о наличии автокорреляции (она тоже включена в пользовательский модуль my_module__stat.py).

ОСНОВЫ ТЕОРИИ

Информацию о критерии Дарбина-Уотсона можно почерпнуть в [1, с.659], [2, с.117], [3, с.239], [4, с.188], а также:

Итак, предположим, мы рассматриваем регрессионную модель:

y_i = b_0 + \displaystyle\sum_{j=1}^{m} b_j x_{ij} + \varepsilon_i, \quad i=\overline{1,n}\widehat{y}_i = b_0 + \displaystyle\sum_{j=1}^{m} b_j x_{ij}, \quad i=\overline{1,n}

или в матричном виде:

\textbf{Y} = \textbf{X}b + \varepsilon\widehat{\textbf{Y}} = \textbf{X}b

Критерий Дарбина-Уотсона применяется в ситуации, когда регрессионные остатки связаны автокорреляционной зависимостью 1-го порядка [2, с.111]:

\varepsilon_i = \rho \varepsilon_{i-1} + \delta_i, \quad i=\overline{2,n}

где \rho — некоторое число (|\rho|<1), а случайные величины \delta_i удовлетворяют требованиям, предъявляемым к регрессионным остаткам классической модели (т.е. равенство нулю среднего значения, постоянство дисперсии и некоррелированность между собой):

E(\delta_i)=0E(\delta_i\delta_j)=\begin{cases}{\sigma_0}^2, & \quad i=j \\0, & \quad i \neq j\end{cases}

Проверяется нулевая гипотеза об отсутствии автокорреляции:

\begin{aligned} \qquad H_0: \rho = 0 \end{aligned}

Альтернативной гипотезой может быть:

  • существование отрицательной автокорреляции (левосторонняя критическая область):

\begin{aligned} \qquad H_1: \rho < 0 \end{aligned}

  • существование положительной автокорреляции (правосторонняя критическая область):

\begin{aligned} \qquad H_1: \rho \neq 0 \end{aligned}

Расчетное значение статистики критерия Дарбина-Уотсона имеет вид:

DW_{calc} = \frac {\displaystyle\sum_{i=2}^{n} (\varepsilon_i - \varepsilon_{i-1})^2} {{\displaystyle\sum_{i=1}^{n} {\varepsilon_i}^2}}

где \varepsilon_i = y_i - \widehat{y}_i — остатки (невязки) регрессионной модели.

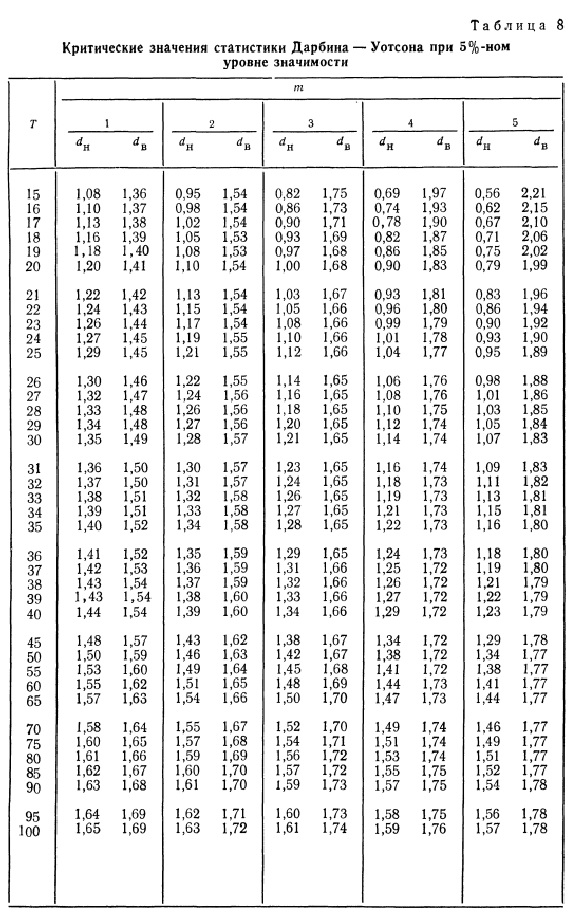
По таблицам (см. [1, с.659], [2, с.402], [3, с.291]) в зависимости от уровня значимости \alpha_{level} (5%, 2.5%, 1%), числа параметров регрессионной модели m (кроме свободного члена b_0) (от 1 до 5) и объема выборки n (от 15 до 100) определяются критические значения статистики Дарбина-Уотсона: нижний d_L и верхний d_U предел.

Правила принятия гипотез по критерию Дарбина-Уотсона выглядят довольно своеобразно — критические значения образуют пять областей различных статистических решений (причем критические границы принятия H_0 и непринятия H_1 не совпадают):

Значение DW_{calc}

Принимается гипотеза

Вывод

0 \leq DW_{calc} < d_L

отвергается H_0, принимается есть положительная автокорреляция

d_L \leq DW_{calc} \leq d_U

неопределенность

d_U < DW_{calc} < 4-d_U

принимается H_0

автокорреляция отсутствует

4-d_U \leq DW_{calc} \leq 4-d_L

неопределенность

4-d_L < DW_{calc} \leq 4

отвергается H_0, принимается H_1: \rho < 0

есть отрицательная автокорреляция

Есть очень удачная мнемоническая схема, приведенная в [3, с.240]:

Особенности критерия Дарбина-Уотсона:

  1. Критические значения критерия табулированы для объема выборки от 15 до 100, аппроксимаций мне обнаружить не удалось. При меньших значениях критерий применять нельзя, при больших — очевидно, приходиться пользоваться грубым оценочным правилом: при расчетном значении статистики критерия в интервале [1; 2] автокорреляция отсутствует (см. https://en.wikipedia.org/wiki/Durbin–Watson_statistic).

  2. Критерий позволяет выявить только автокорреляцию 1-го порядка. Отклонение нулевой гипотезы не означает, что автокорреляции нет вообще — возможно наличие автокорреляции более высоких порядков.

  3. Критерий построен в предположении, что регрессоры \textbf{X} и ошибки \varepsilon не коррелированы, поэтому его нельзя применять, в частности, для моделей авторегрессии [4, с.191].

  4. Критерий не подходит для моделей без свободного члена b_0.

  5. Критерий имеет зону неопределенности, когда нет оснований ни принимать, ни отвергать нулевую гипотезу.

  6. Между статистикой критерия и коэффициентом автокорреляции существует приближенное соотношение:

DW_{calc} \approx 2 \cdot (1-\rho)

Существуют и другие критерии для проверки автокорреляции (тест Бройша-Годфри, Льюнга-Бокса и пр.).

Как было указано выше, большой проблемой является отсутствие табличных значений статистики критерия Дарбина-Уостона в стандартном инструментарии python. Для реализации возможностей данного критерия в полном объеме нам потребуется оцифровка весьма объемных таблиц критических значений.

ОЦИФРОВКА ТАБЛИЧНЫХ ЗНАЧЕНИЙ СТАТИСТИКИ КРИТЕРИЯ ДАРБИНА-УОТСОНА

Я решил добавить в обзор этот раздел, хотя, строго говоря, можно было обойтись и без него, а сразу воспользоваться оцифрованными таблицами статистики критерия Дарбина-Уотсона.

Однако, если мы хотим выполнять качественный статистический анализ, неизбежно придется работать с большим количеством статистических критериев и далеко не все из них реализованы в python. Критерий Дарбина-Уотсона — это только один из многих. Количество критериев, рассматриваемых в литературе по прикладной статистике в последние годы постоянно увеличивается. Специалисту придется реализовывать многие критерии самостоятельно и одна из проблем, с которой придется столкнуться — это таблицы критических значений. Далеко не все табличные значения имеют аппроксимации, а значит придется каким-то образом оцифровывать эти таблицы. Небольшие таблицы можно сохранить в файлах вручную, а вот такой подход с объемными таблицами (как в нашем случае) — это слишком непроизводительно и нерационально.

В общем, на мой взгляд, представляет интерес разобрать пример оцифровки статистических таблиц на примере нашего критерия Дарбина-Уотсона — это позволит специалистам сэкономить человеко-часы работы и облегчить совершенствование инструментов статистического анализа.

Замечу сразу, что я не являюсь глубоким специалистом в области анализа и обработки изображений и текстов на python — это не совсем мой профиль. Профессионалы в этой области, возможно, раскритикуют то, как решается поставленная задача и предложат более удачное решение. Если будет так — то заранее спасибо. Я же эту задачу старался решить наиболее простым и рациональным способом, доступным для широкого круга специалистов. На всякий случай могу процитировать Давоса Сиворта из «Игры престолов»: «Простите за то, что увидите».

Алгоритм действий:

Для оцифровки я использовал таблицы, приведенные в [3, с.290-292].

  1. Сканируем таблицы, сохраняем в виде jpg-файлов (Durbin_Watson_test_1.jpg, Durbin_Watson_test_2.jpg, Durbin_Watson_test_3.jpg) в папке text_processing, расположенной внутри папки с рабочим .ipynb-файлом:

  1. Распознаем текст (я воспользовался онлайн-сервисом https://convertio.co/), полученные текстовые файлы Durbin-Watson-test-1.ocr.txt, Durbin-Watson-test-2.ocr.txt, Durbin-Watson-test-3.ocr.txt также помещаем в папке text_processing.

  2. Откроем файлы, запишем содержимое файлов в переменные, каждая из которых соответствует одной странице:

with open('text_processing\Durbin-Watson-test-1.ocr.txt') as f1:     Durbin_Watson_test_1 = f1.readlines() display(Durbin_Watson_test_1, type(Durbin_Watson_test_1), len(Durbin_Watson_test_1))

С остальными файлами — действуем аналогично:

with open('text_processing\Durbin-Watson-test-2.ocr.txt') as f2:     Durbin_Watson_test_2 = f2.readlines() display(Durbin_Watson_test_2, type(Durbin_Watson_test_2), len(Durbin_Watson_test_2))  with open('text_processing\Durbin-Watson-test-3.ocr.txt') as f3:     Durbin_Watson_test_3 = f3.readlines() display(Durbin_Watson_test_3, type(Durbin_Watson_test_3), len(Durbin_Watson_test_3))

Видим, что переменные представляют собой списки, элементами которых является строки.

Для облегчения дальнейшей обработки данных создадим список, элементами которого являются переменные-страницы:

Durbin_Watson_test = [Durbin_Watson_test_1, Durbin_Watson_test_2, Durbin_Watson_test_3]

Далее я не стал публиковать здесь скриншоты с обработкой страниц — из-за экономии места. В ipyng-файле, который доступен в моем репозитории, весь процесс обработки представлен достаточно подробно.

  1. Исключаем все строки, которые начинаются не с цифр; при этом воспользуемся алгоритмом перезаписи списка:

# создаем новый список Durbin_Watson_test_new = list()  # удаляем строки for page in Durbin_Watson_test:     page_temp = list()    # временная страница     for line in page:         if line[0].isdigit():             page_temp.append(line)    # перезаписываем список     Durbin_Watson_test_new.append(page_temp)

  1. Исключаем из текста управляющие символы (\t, \n) — с помощью регулярных выражений (regex) (модуль re):

# задаем шаблон для удаления символов pattern = r'[\t+\n+]'      # выполняем обработку Durbin_Watson_test_new = [     [re.sub(pattern, '  ', elem) for elem in page]      for page in Durbin_Watson_test_new]

  1. Удаляем все символы, кроме цифр, точек, запятых и пробелов:

# задаем шаблон для удаления символов pattern = r'[^0-9,. ]'      # выполняем обработку Durbin_Watson_test_new = [     [re.sub(pattern, '', elem) for elem in page]      for page in Durbin_Watson_test_new]

  1. Заменяем запятые на точки:

# задаем шаблон для удаления символов pattern = r'[,]'  # выполняем обработку Durbin_Watson_test_new = [     [re.sub(pattern, '.', elem) for elem in page]      for page in Durbin_Watson_test_new]

  1. Разделяем строки:

# задаем шаблон pattern = r'[ ]+'  # выполняем обработку Durbin_Watson_test_new = [[re.split(pattern, elem) for elem in page]                            for page in Durbin_Watson_test_new]

  1. Сохраняем данные в DataFrame — для этого создадим список Durbin_Watson_list_df, элементами которого являются отдельные DataFrame, каждый из которых соответствует отдельной странице:

# создаем новый список Durbin_Watson_list_df = list() for page in Durbin_Watson_test_new:     Durbin_Watson_list_df.append(pd.DataFrame(page))

  1. Исправляем вручную отдельные аномалии, возникшие при распознавании отсканированных данных — к сожалению, работы вручную совсем избежать не удается.

  • Корректируем DataFrame, соответствующий 1-й странице:

# создаем временный DataFrame temp_df = Durbin_Watson_list_df[0] # удаляем последние столбцы temp_df = temp_df.drop(columns=[11, 12]) # корректируем вручную отдельные ошибки temp_df.loc[[4],] = [19, 1.18, 1.40, 1.08, 1.53, 0.97, 1.68, 0.86, 1.85, 0.75, 2.02] temp_df.loc[[8],[3]] = 1.17 temp_df.loc[[10],[3]] = 1.21 temp_df.loc[[17],[9]] = 1.11 temp_df.loc[[21],[4]] = 1.59 temp_df.loc[[25],[5]] = 1.34 temp_df.loc[[31],[10]] = 1.77 # записываем изменения Durbin_Watson_list_df[0] = temp_df

  • Корректируем DataFrame, соответствующий 2-й странице:

# создаем временный DataFrame temp_df = Durbin_Watson_list_df[1] # удаляем последние столбцы temp_df = temp_df.drop(columns=[11, 12]) # корректируем вручную отдельные ошибки temp_df.loc[[2],[8]] = 1.77 temp_df.loc[[10],[9]] = 0.86 temp_df.loc[[10],[10]] = 1.77 temp_df.loc[[14],[9]] = 0.96 temp_df.loc[[17],[10]] = 1.71 temp_df.loc[[34],[10]] = 1.71 # записываем изменения Durbin_Watson_list_df[1] = temp_df

  • Корректируем DataFrame, соответствующий 3-й странице:

# создаем временный DataFrame temp_df = Durbin_Watson_list_df[2] # удаляем последние столбцы temp_df = temp_df.drop(columns=[11, 12]) # корректируем вручную отдельные ошибки temp_df.loc[[2],[9]] = 0.48 temp_df.loc[[13],] = [28, 1.10, 1.24, 1.04, 1.32, 0.97, 1.41, 0.90, 1.51, 0.83, 1.62] temp_df.loc[[20],[3]] = 1.14 temp_df.iloc[21:26, 7] = [1.04, 1.06, 1.07, 1.09, 1.10] temp_df.loc[[26],[9]] = 1.11 temp_df.loc[[35],] = [90, 1.50, 1.54, 1.47, 1.56, 1.45, 1.59, 1.43, 1.61, 1.41, 1.64] # записываем изменения Durbin_Watson_list_df[2] = temp_df

Обращаем внимание, что откорректированные вручную значения являются числовыми, а все остальные значения — еще имеют строковый тип.

11. Преобразуем значения из строкового в числовой тип:

for elem_df in Durbin_Watson_list_df:     for col in elem_df.columns:         elem_df[col] = pd.to_numeric(elem_df[col], errors='ignore')

  1. Корректируем структуру DataFrame:

  • меняем индекс — индексом теперь будет объем выборки n

  • каждый DataFrame снабжаем мультииндексом по столбцам (подробнее см. [7, с.169])

# меняем индекс Durbin_Watson_list_df = [     elem_df.set_index([0])     for elem_df in Durbin_Watson_list_df]  # добавляем мультииндекс по столбцам multi_index_list = ['p=0.95', 'p=0.975', 'p=0.99']    # список, содержащий значения для верхней строки мульииндекса for i, elem_df in enumerate(Durbin_Watson_list_df):     elem_df.index.name = 'n'     elem_df.columns = pd.MultiIndex.from_product(         [[multi_index_list[i]],          ['m=1', 'm=2', 'm=3', 'm=4', 'm=5'],          ['dL','dU']])

  1. Объединяем отдельные DataFrame в один:

Durbin_Watson_test_df = Durbin_Watson_list_df[0].copy()  for i, elem_df in enumerate(Durbin_Watson_list_df):     if i > 0:         Durbin_Watson_test_df = Durbin_Watson_test_df.join(elem_df)  display(Durbin_Watson_test_df)        
Durbin_Watson_test_df.info()

Итак, мы сформировали DataFrame с оцифрованными данными таблиц критических значений статистики Дарбина-Уотсона. Получить доступ к данным теперь очень просто — например, нам требуется вывести табличные значения статистики критерия при объеме выборки n=40, доверительной вероятности p=0.95 и числе параметров регрессионной модели m=2:

n = 40 p = 0.95 m=2  Durbin_Watson_test_df.loc[[n], (f'p={p}', f'm={m}')]

  1. Построим график табличных значений.

График получился весьма объемным — 3х5 элементов — однако он необходим: на графике можно увидеть те ошибки (пики и впадины), которые мы могли пропустить при ручной обработке ранее (некорректно отсканированные и распознанные цифры), тогда придется вернуться к этапу 10.

# меняем настройки Mathplotlib plt.rcParams['axes.titlesize'] = 10      # шрифт заголовка plt.rcParams['legend.fontsize'] = 9      # шрифт легенды plt.rcParams['xtick.labelsize'] = 8      # шрифт подписей меток plt.rcParams['ytick.labelsize'] = 8  fig = plt.figure(figsize=(297/INCH, 420/INCH))  ax_1_1 = plt.subplot(5,3,1) ax_2_1 = plt.subplot(5,3,2) ax_3_1 = plt.subplot(5,3,3) ax_1_2 = plt.subplot(5,3,4) ax_2_2 = plt.subplot(5,3,5) ax_3_2 = plt.subplot(5,3,6) ax_1_3 = plt.subplot(5,3,7) ax_2_3 = plt.subplot(5,3,8) ax_3_3 = plt.subplot(5,3,9) ax_1_4 = plt.subplot(5,3,10) ax_2_4 = plt.subplot(5,3,11) ax_3_4 = plt.subplot(5,3,12) ax_1_5 = plt.subplot(5,3,13) ax_2_5 = plt.subplot(5,3,14) ax_3_5 = plt.subplot(5,3,15)  fig.suptitle('Табличные значения статистики критерия Дарбина-Уотсона', fontsize = 16)  (Ymin, Ymax) = (0.3, 2.2) x = Durbin_Watson_test_df.index  title_fontsize = 10  name_1_1 = ['p=0.95', 'm=1'] ax_1_1.set_title(name_1_1[0] + ' ' + name_1_1[1]) ax_1_1.plot(x, Durbin_Watson_test_df[tuple(name_1_1 + ['dL'])],             x, Durbin_Watson_test_df[tuple(name_1_1 + ['dU'])])  name_1_2 = ['p=0.95', 'm=2'] ax_1_2.set_title(name_1_2[0] + ' ' + name_1_2[1]) ax_1_2.plot(x, Durbin_Watson_test_df[tuple(name_1_2 + ['dL'])],             x, Durbin_Watson_test_df[tuple(name_1_2 + ['dU'])])  name_1_3 = ['p=0.95', 'm=3'] ax_1_3.set_title(name_1_3[0] + ' ' + name_1_3[1]) ax_1_3.plot(x, Durbin_Watson_test_df[tuple(name_1_3 + ['dL'])],             x, Durbin_Watson_test_df[tuple(name_1_3 + ['dU'])])  name_1_4 = ['p=0.95', 'm=4'] ax_1_4.set_title(name_1_4[0] + ' ' + name_1_4[1]) ax_1_4.plot(x, Durbin_Watson_test_df[tuple(name_1_4 + ['dL'])],             x, Durbin_Watson_test_df[tuple(name_1_4 + ['dU'])])  name_1_5 = ['p=0.95', 'm=5'] ax_1_5.set_title(name_1_5[0] + ' ' + name_1_5[1]) ax_1_5.plot(x, Durbin_Watson_test_df[tuple(name_1_5 + ['dL'])],             x, Durbin_Watson_test_df[tuple(name_1_5 + ['dU'])])  name_2_1 = ['p=0.975', 'm=1'] ax_2_1.set_title(name_2_1[0] + ' ' + name_2_1[1]) ax_2_1.plot(x, Durbin_Watson_test_df[tuple(name_2_1 + ['dL'])],             x, Durbin_Watson_test_df[tuple(name_2_1 + ['dU'])])  name_2_2 = ['p=0.975', 'm=2'] ax_2_2.set_title(name_2_2[0] + ' ' + name_2_2[1]) ax_2_2.plot(x, Durbin_Watson_test_df[tuple(name_2_2 + ['dL'])],             x, Durbin_Watson_test_df[tuple(name_2_2 + ['dU'])])  name_2_3 = ['p=0.975', 'm=3'] ax_2_3.set_title(name_2_3[0] + ' ' + name_2_3[1]) ax_2_3.plot(x, Durbin_Watson_test_df[tuple(name_2_3 + ['dL'])],             x, Durbin_Watson_test_df[tuple(name_2_3 + ['dU'])])  name_2_4 = ['p=0.975', 'm=4'] ax_2_4.set_title(name_2_4[0] + ' ' + name_2_4[1]) ax_2_4.plot(x, Durbin_Watson_test_df[tuple(name_2_4 + ['dL'])],             x, Durbin_Watson_test_df[tuple(name_2_4 + ['dU'])])  name_2_5 = ['p=0.975', 'm=5'] ax_2_5.set_title(name_2_5[0] + ' ' + name_2_5[1]) ax_2_5.plot(x, Durbin_Watson_test_df[tuple(name_2_5 + ['dL'])],             x, Durbin_Watson_test_df[tuple(name_2_5 + ['dU'])])  name_3_1 = ['p=0.99', 'm=1'] ax_3_1.set_title(name_3_1[0] + ' ' + name_3_1[1]) ax_3_1.plot(x, Durbin_Watson_test_df[tuple(name_3_1 + ['dL'])],             x, Durbin_Watson_test_df[tuple(name_3_1 + ['dU'])])  name_3_2 = ['p=0.99', 'm=2'] ax_3_2.set_title(name_3_2[0] + ' ' + name_3_2[1]) ax_3_2.plot(x, Durbin_Watson_test_df[tuple(name_3_2 + ['dL'])],             x, Durbin_Watson_test_df[tuple(name_3_2 + ['dU'])])  name_3_3 = ['p=0.99', 'm=3'] ax_3_3.set_title(name_3_3[0] + ' ' + name_3_3[1]) ax_3_3.plot(x, Durbin_Watson_test_df[tuple(name_3_3 + ['dL'])],             x, Durbin_Watson_test_df[tuple(name_3_3 + ['dU'])])  name_3_4 = ['p=0.99', 'm=4'] ax_3_4.set_title(name_3_4[0] + ' ' + name_3_4[1]) ax_3_4.plot(x, Durbin_Watson_test_df[tuple(name_3_4 + ['dL'])],             x, Durbin_Watson_test_df[tuple(name_3_4 + ['dU'])])  name_3_5 = ['p=0.99', 'm=5'] ax_3_5.set_title(name_3_5[0] + ' ' + name_3_5[1]) ax_3_5.plot(x, Durbin_Watson_test_df[tuple(name_3_5 + ['dL'])],             x, Durbin_Watson_test_df[tuple(name_3_5 + ['dU'])])  ax_1_1.set_ylim(Ymin, Ymax) ax_2_1.set_ylim(Ymin, Ymax) ax_3_1.set_ylim(Ymin, Ymax) ax_1_2.set_ylim(Ymin, Ymax) ax_2_2.set_ylim(Ymin, Ymax) ax_3_2.set_ylim(Ymin, Ymax) ax_1_3.set_ylim(Ymin, Ymax) ax_2_3.set_ylim(Ymin, Ymax) ax_3_3.set_ylim(Ymin, Ymax) ax_1_4.set_ylim(Ymin, Ymax) ax_2_4.set_ylim(Ymin, Ymax) ax_3_4.set_ylim(Ymin, Ymax) ax_1_5.set_ylim(Ymin, Ymax) ax_2_5.set_ylim(Ymin, Ymax) ax_3_5.set_ylim(Ymin, Ymax)  legend = (r'$d_L$', r'$d_U$') ax_1_1.legend(legend) ax_2_1.legend(legend) ax_3_1.legend(legend) ax_1_2.legend(legend) ax_2_2.legend(legend) ax_3_2.legend(legend) ax_1_3.legend(legend) ax_2_3.legend(legend) ax_3_3.legend(legend) ax_1_4.legend(legend) ax_2_4.legend(legend) ax_3_4.legend(legend) ax_1_5.legend(legend) ax_2_5.legend(legend) ax_3_5.legend(legend)  plt.show()  # возвращаем настройки Mathplotlib plt.rcParams['axes.titlesize'] = f_size + 10      # шрифт заголовка plt.rcParams['legend.fontsize'] = f_size + 6      # шрифт легенды plt.rcParams['xtick.labelsize'] = f_size + 4      # шрифт подписей меток plt.rcParams['ytick.labelsize'] = f_size + 4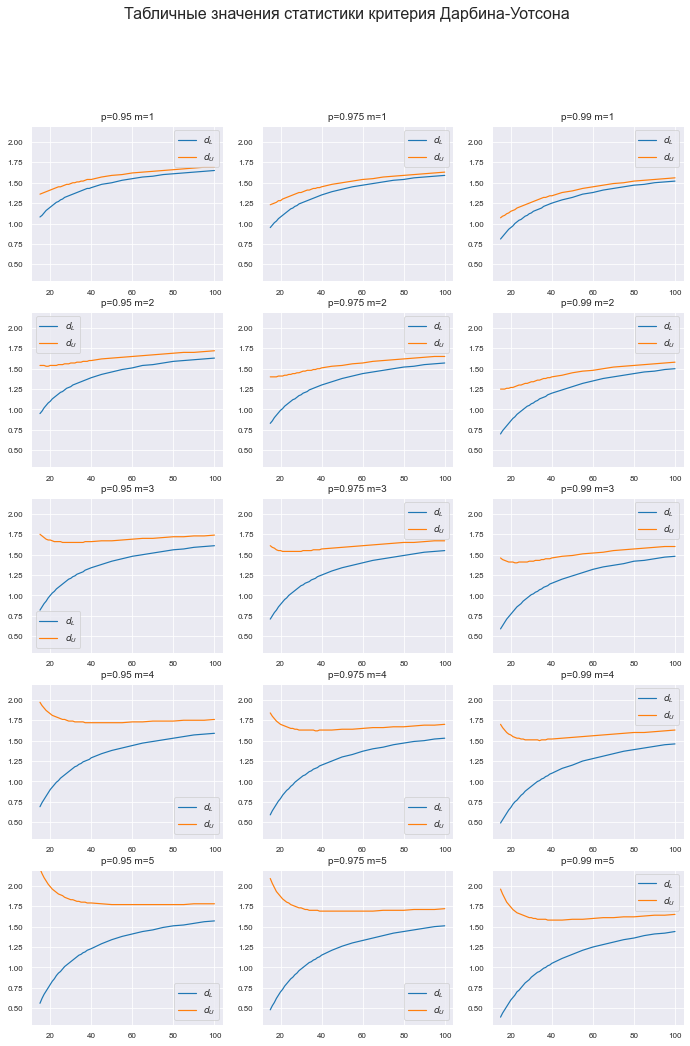

  1. Сохраняем полученный DataFrame в csv-файл, помещаем его в папку table, расположенную внутри папки с рабочим .ipynb-файлом (в которой папку table у нас хранятся файлы с данными из статистических таблиц):

Durbin_Watson_test_df.to_csv(     path_or_buf='table\Durbin_Watson_test_table.csv',     mode='w+',     sep=';',     index_label='n')

Табличные значения статистики критерия Дарбина-Уотсона у нас теперь имеются, можем приступать к созданию пользовательской функции.

СОЗДАНИЕ ПОЛЬЗОВАТЕЛЬСКОЙ ФУНКЦИИ ДЛЯ РЕАЛИЗАЦИИ КРИТЕРИЯ ДАРБИНА-УОТСОНА

Рассчитать статистику критерия Дарбина-Уотсона мы можем с помощью функции statsmodels.stats.stattools.durbin_watson.
Создадим пользовательскую функцию Durbin_Watson_test для проверки гипотезы об автокорреляции:

def Durbin_Watson_test(     data,     m = None,     p_level: float=0.95):          a_level = 1 - p_level     data = np.array(data)     n = len(data)          # расчетное значение статистики критерия     DW_calc = sms.stattools.durbin_watson(data)          # табличное значение статистики критерия     if (n >= 15) and (n <= 100):         # восстанавливаем структуру DataFrame из csv-файла         DW_table_df = pd.read_csv(             filepath_or_buffer='table/Durbin_Watson_test_table.csv',             sep=';',             #index_col='n'             )                                      DW_table_df = DW_table_df.rename(columns={'Unnamed: 0': 'n'})         DW_table_df = DW_table_df.drop([0, 1, 2])                  for col in DW_table_df.columns:             DW_table_df[col] = pd.to_numeric(DW_table_df[col], errors='ignore')                      DW_table_df = DW_table_df.set_index('n')          DW_table_df.columns = pd.MultiIndex.from_product(             [['p=0.95', 'p=0.975', 'p=0.99'],             ['m=1', 'm=2', 'm=3', 'm=4', 'm=5'],             ['dL','dU']])                      # интерполяция табличных значений         key = [f'p={p_level}', f'm={m}']         f_lin_L = sci.interpolate.interp1d(DW_table_df.index, DW_table_df[tuple(key + ['dL'])])         f_lin_U = sci.interpolate.interp1d(DW_table_df.index, DW_table_df[tuple(key + ['dU'])])         DW_table_L = float(f_lin_L(n))         DW_table_U = float(f_lin_U(n))                             # проверка гипотезы         Durbin_Watson_scale = {             1: DW_table_L,             2: DW_table_U,             3: 4 - DW_table_U,             4: 4 - DW_table_L,             5: 4}                  Durbin_Watson_comparison = {             1: ['0 ≤ DW_calc < DW_table_L',                   'H1: r > 0'],             2: ['DW_table_L ≤ DW_calc ≤ DW_table_U',          'uncertainty'],             3: ['DW_table_U < DW_calc < 4 - DW_table_U',      'H0: r = 0'],             4: ['4 - DW_table_U ≤ DW_calc ≤ 4 - DW_table_L',  'uncertainty'],             5: ['4 - DW_table_L < DW_calc ≤ 4',               'H1: r < 0']}                  r_scale = list(Durbin_Watson_scale.values())         for i, elem in enumerate(r_scale):             if DW_calc <= elem:                 key_scale = list(Durbin_Watson_scale.keys())[i]                 comparison = Durbin_Watson_comparison[key_scale][0]                 conclusion = Durbin_Watson_comparison[key_scale][1]                 break                 elif n < 15:                 comparison = '-'         conclusion = 'count less than 15'     else:         comparison = '-'         conclusion = 'count more than 100'               # формируем результат                 result = pd.DataFrame({         'n': (n),         'm': (m),         'p_level': (p_level),         'a_level': (a_level),         'DW_calc': (DW_calc),         'ρ': (1 - DW_calc/2),         'DW_table_L': (DW_table_L if (n >= 15) and (n <= 100) else '-'),         'DW_table_U': (DW_table_U if (n >= 15) and (n <= 100) else '-'),         'comparison of calculated and critical values': (comparison),         'conclusion': (conclusion)         },         index=['Durbin-Watson_test'])               return result

Протестируем созданную функцию — будем моделировать временные ряды с различными свойствами и выполнять проверку автокорреляции:

y_func = lambda x, b0, b1: b0 + b1*x  N = 30    # число наблюдений (mu, sigma) = (0, 25)    # параметры моделируемой случайной компоненты (среднее и станд.отклонение)

  1. Смоделируем временной ряд с трендом, без автокорреляции остатков:

# моделирование T_model = np.linspace(1, N, N)    # независимая переменная - номер наблюдения (b0, b1) = (100, 5)    # параметры моделируемого временного ряда Y_model = np.array(y_func(T_model, b0, b1)) + np.random.normal(mu, sigma, N)  # визуализация axes = sns.jointplot(     x=T_model, y=Y_model,     kind='reg') plt.show()  # проверка автокорреляции display(Durbin_Watson_test(Y_model, m=1, p_level=0.95))
# моделирование T_model = np.linspace(1, N, N)    # независимая переменная - номер наблюдения (b0, b1) = (100, -5)    # параметры моделируемого временного ряда Y_model = np.array(y_func(T_model, b0, b1)) + np.random.normal(mu, sigma, N)  # визуализация axes = sns.jointplot(     x=T_model, y=Y_model,     kind='reg') plt.show()  # проверка автокорреляции display(Durbin_Watson_test(Y_model, m=1, p_level=0.95))

  1. Смоделируем временной ряд без тренда:

# моделирование T_model = np.linspace(1, N, N)    # независимая переменная - номер наблюдения (b0, b1) = (100, 0)    # параметры моделируемого временного ряда Y_model = np.array(y_func(T_model, b0, b1)) + np.random.normal(mu, sigma, N)  # визуализация axes = sns.jointplot(     x=T_model, y=Y_model,     kind='reg') plt.show()  # проверка автокорреляции display(Durbin_Watson_test(Y_model, m=1, p_level=0.95))
# моделирование T_model = np.linspace(1, N, N)    # независимая переменная - номер наблюдения (b0, b1) = (0, 0)    # параметры моделируемого временного ряда Y_model = np.array(y_func(T_model, b0, b1)) + np.random.normal(mu, sigma, N)  # визуализация axes = sns.jointplot(     x=T_model, y=Y_model,     kind='reg') plt.show()  # проверка автокорреляции display(Durbin_Watson_test(Y_model, m=1, p_level=0.95))

  1. Смоделируем временной ряд с трендом, с положительной автокорреляцией:

# моделирование T_model = np.linspace(1, N, N)    # независимая переменная - номер наблюдения (b0, b1) = (100, 5)    # параметры моделируемого временного ряда  E = np.array([np.random.normal(mu, sigma, 1)]) r = 0.9 for i in range(1, N):     elem = r*E[i-1] + np.random.normal(mu, sigma, 1)     E = np.append(E, elem) Y_model = np.array(y_func(T_model, b0, b1)) + E  # визуализация axes = sns.jointplot(     x=T_model, y=Y_model,     kind='reg') plt.show()  # проверка автокорреляции display(Durbin_Watson_test(Y_model, m=1, p_level=0.95))

  1. Смоделируем временной ряд с трендом, с отрицательной автокорреляцией:

# моделирование T_model = np.linspace(1, N, N)    # независимая переменная - номер наблюдения (b0, b1) = (100, 5)    # параметры моделируемого временного ряда  E = np.array([np.random.normal(mu, sigma, 1)]) r = -0.9 for i in range(1, N):     elem = r*E[i-1] + np.random.normal(mu, sigma, 1)     E = np.append(E, elem) Y_model = np.array(y_func(T_model, b0, b1)) + E  # визуализация axes = sns.jointplot(     x=T_model, y=Y_model,     kind='reg') plt.show()  # проверка автокорреляции display(Durbin_Watson_test(Y_model, m=1, p_level=0.95))

  1. Смоделируем временной ряд без тренда, с положительной автокорреляцией:

# моделирование T_model = np.linspace(1, N, N)    # независимая переменная - номер наблюдения (b0, b1) = (100, 0)    # параметры моделируемого временного ряда  E = np.array([np.random.normal(mu, sigma, 1)]) r = 0.9 for i in range(1, N):     elem = r*E[i-1] + np.random.normal(mu, sigma, 1)     E = np.append(E, elem) Y_model = np.array(y_func(T_model, b0, b1)) + E  # визуализация axes = sns.jointplot(     x=T_model, y=Y_model,     kind='reg') plt.show()  # проверка автокорреляции display(Durbin_Watson_test(Y_model, m=1, p_level=0.95))
# моделирование T_model = np.linspace(1, N, N)    # независимая переменная - номер наблюдения (b0, b1) = (0, 0)    # параметры моделируемого временного ряда  E = np.array([np.random.normal(mu, sigma, 1)]) r = 0.9 for i in range(1, N):     elem = r*E[i-1] + np.random.normal(mu, sigma, 1)     E = np.append(E, elem) Y_model = np.array(y_func(T_model, b0, b1)) + E  # визуализация axes = sns.jointplot(     x=T_model, y=Y_model,     kind='reg') plt.show()  # проверка автокорреляции display(Durbin_Watson_test(Y_model, m=1, p_level=0.95))

  1. Смоделируем временной ряд без тренда, с отрицательной автокорреляцией:

# моделирование T_model = np.linspace(1, N, N)    # независимая переменная - номер наблюдения (b0, b1) = (100, 0)    # параметры моделируемого временного ряда  E = np.array([np.random.normal(mu, sigma, 1)]) r = -0.9 for i in range(1, N):     elem = r*E[i-1] + np.random.normal(mu, sigma, 1)     E = np.append(E, elem) Y_model = np.array(y_func(T_model, b0, b1)) + E  # визуализация axes = sns.jointplot(     x=T_model, y=Y_model,     kind='reg') plt.show()  # проверка автокорреляции display(Durbin_Watson_test(Y_model, m=1, p_level=0.95))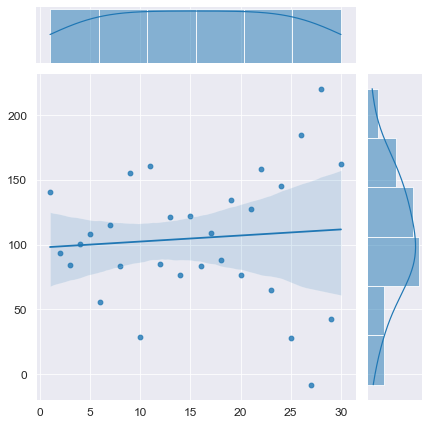
# моделирование T_model = np.linspace(1, N, N)    # независимая переменная - номер наблюдения (b0, b1) = (0, 0)    # параметры моделируемого временного ряда  E = np.array([np.random.normal(mu, sigma, 1)]) r = -0.9 for i in range(1, N):     elem = r*E[i-1] + np.random.normal(mu, sigma, 1)     E = np.append(E, elem) Y_model = np.array(y_func(T_model, b0, b1)) + E  # визуализация axes = sns.jointplot(     x=T_model, y=Y_model,     kind='reg') plt.show()  # проверка автокорреляции display(Durbin_Watson_test(Y_model, m=1, p_level=0.95))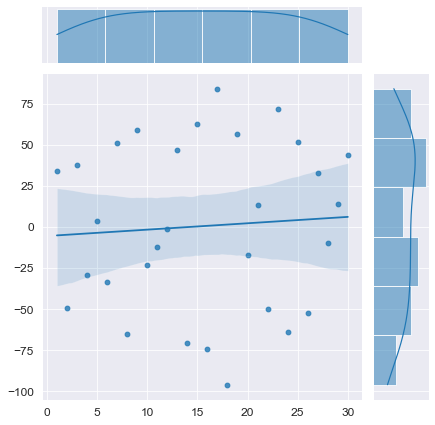

Конечно, данный вычислительный эксперимент не может претендовать на всеобъемлемость, однако определенный любопытный предварительный вывод можно сделать: при наличии любого тренда (даже если этот тренда представляет собой равенство постоянной величине Y=b_0 + \varepsilon) критерий Дарбина-Уотсона выдает нам наличие положительной автокорреляции (даже если в модели автокорреляция не заложена нет или она отрицательная). Такой вывод нужно исследовать более глубоко, но это не входит в цель данного обзора. Специалист должен помнить об особенностях критерия Дарбина-Уотсона.

Теперь мы можем перейти к практическим примерам.

ПРИМЕР 1: проверка автокорреляции модели временного ряда

Формирование исходных данных

В качестве исходных данных рассмотрим динамику показателей индексов пересчета сметной стоимости проектно-изыскательских работ в РФ. Эти показатели ежеквартально публикует Министерство строительства и ЖКХ РФ, а все проектные и изыскательские организации используют эти показатели при составлении смет на свои работы.

В данном случае мы имеем набор показателей в виде временного ряда, для которого будем строить регрессионную модель долговременной тенденции (тренда), и остатки этой регрессионной модели будем исследовать на автокорреляцию.

Исходные данные содержаться в файле Ежеквартальные индексы ПИР.xlsx, который помещен в папку data.

Прочитаем xlsx-файл:

data_df = pd.read_excel('data/Ежеквартальные индексы ПИР.xlsx', sheet_name='БД')   #display(data_df) display(data_df.head(), data_df.tail()) data_df.info()

Не будем подробно останавливаться на содержимом файла и его первичной обработке — это выходит за пределы данного обзора. Специалисты, причастные к сфере строительства и проектирования, поймут, а для остальных специалистов эти цифры можно воспринимать по аналогии с индексами инфляции Росстата и Минэкономразвития.

Прочитаем из этого файла интересующие нас данные — индексы изменения сметной стоимости проектных работ к уровню цен на 01.01.2001 г.:

Ind_design_2001 = np.array(data_df['Ипроект2001']) print(Ind_design_2001, '\n', type(Ind_design_2001), len(Ind_design_2001))

Сохраним также вспомогательные (технические) переменные, необходимые при анализе временных рядов — дату (Date) и номер наблюдения (T):

# Дата показателя Date = np.array(data_df['ДАТА'])  # Номер наблюдения T = np.array(data_df['N'])

Для удобства дальнейшей работы сформируем сформируем отдельный DataFrame:

dataset_df = pd.DataFrame({     'T': T,     'Date': Date,     'Ind_design_2001': Ind_design_2001}) display(dataset_df.head(), dataset_df.tail())

Визуализация

Настройка заголовков:

# Общий заголовок проекта Task_Project = "Анализ динамики индексов изменения сметной стоимости проектно-изыскательских работ в РФ" # Заголовок, фиксирующий момент времени AsOfTheDate = "за 2008-2022 гг." # Заголовок раздела проекта Task_Theme = "" # Общий заголовок проекта для графиков Title_String = f"{Task_Project}\n{AsOfTheDate}" # Наименования переменных Variable_Name_T_month = "Ежемесячные данные" Variable_Name_Ind_design_2001 = "Индекс изменения сметной стоимости проектных работ к уровню цен на 01.01.2001 г."  # Границы значений переменных (при построении графиков): (X_min_graph, X_max_graph) = (0.0, max(T)) (Y_min_graph, Y_max_graph) = (2.0, 6.0)
graph_plot_sns_np(     Date, Ind_design_2001,     Ymin_in=Y_min_graph, Ymax_in=Y_max_graph,     color='orange',     title_figure=Title_String, title_figure_fontsize=12,     title_axes=Variable_Name_Ind_design_2001, title_axes_fontsize=15,     x_label=Variable_Name_T_month, label_fontsize=12)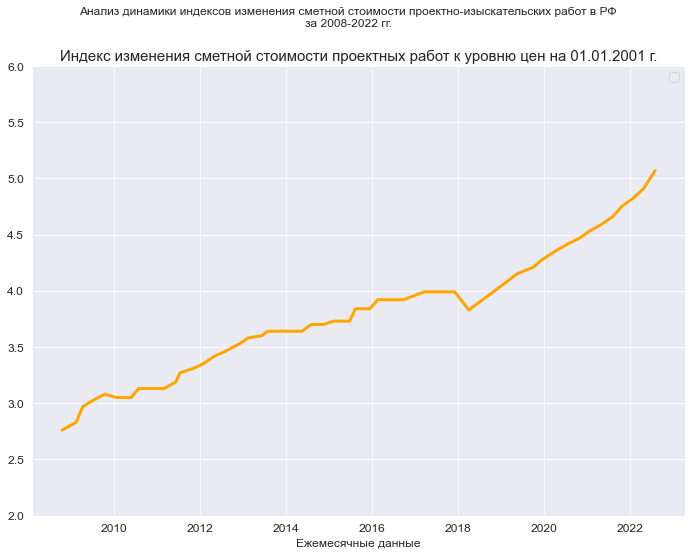

Построение и анализ регрессионной модели

Построим линейную регрессионную модель и проведем ее экспресс-анализ:

model_linear_ols_1 = smf.ols(formula='Ind_design_2001 ~ T', data=dataset_df) result_linear_ols_1 = model_linear_ols_1.fit() print(result_linear_ols_1.summary2())

Формализация модели:

# Функция линейной регрессионной модели (SLRM - simple linear regression model) SLRM_func = lambda x, b0, b1: b0 + b1*x  # параметры модели b0 = result_linear_ols_1.params['Intercept'] b1 = result_linear_ols_1.params['T']  # уравнение модели regr_model_linear_ols_1_func = lambda x: SLRM_func(x, b0, b1)

График модели:

R2 = round(result_linear_ols_1.rsquared, DecPlace) legend_equation = f'линейная регрессия ' + r'$Y$' + f' = {b0:.4f} + {b1:.5f}{chr(183)}' + r'$X$' if b1 > 0 else \                   f'линейная регрессия ' + r'$Y$' + f' = {b0:.4f} - {abs(b1):.5f}{chr(183)}' + r'$X$'  # Пользовательская функция graph_regression_plot_sns(     T, Ind_design_2001,     regression_model=regr_model_linear_ols_1_func,     #Xmin=X_min_graph, Xmax=X_max_graph,     Ymin=Y_min_graph, Ymax=Y_max_graph,     display_residuals=True,     title_figure=Variable_Name_Ind_design_2001, title_figure_fontsize=16,     title_axes = 'Линейная регрессионная модель',     x_label=Variable_Name_T_month,     #y_label=Variable_Name_Ind_design_2001,     label_legend_regr_model = legend_equation + '\n' + r'$R^2$' + f' = {R2}',     s=60)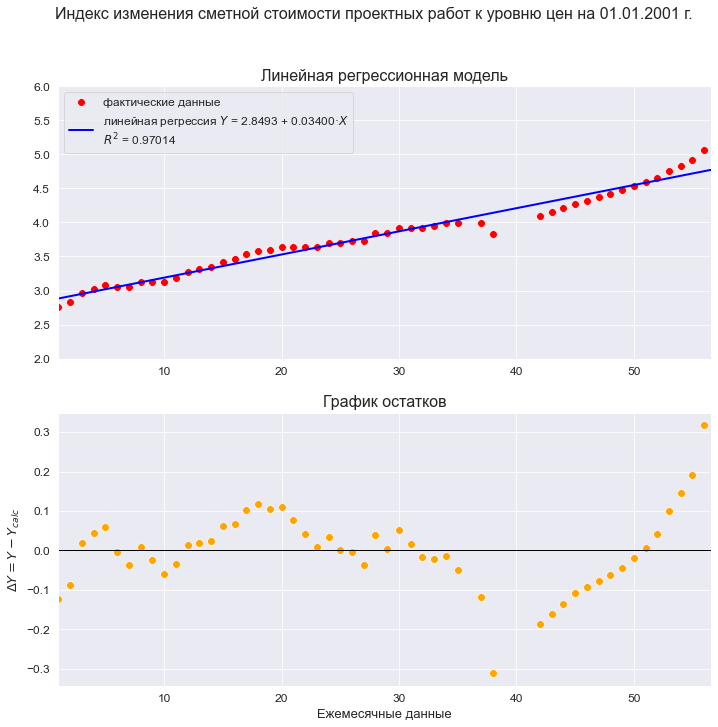

Ошибки аппроксимации модели:

(model_error_metrics, result) = regression_error_metrics(model_linear_ols_1, model_name='linear_ols') display(result)

Проверка нормальности распределения остатков:

res_Y_1 = np.array(result_linear_ols_1.resid)  # Пользовательская функция graph_hist_boxplot_probplot_sns(     data=res_Y_1,     data_min=-0.25, data_max=0.25,     graph_inclusion='hbp',     data_label=r'$ΔY = Y - Y_{calc}$',     #title_figure=Task_Project,     title_axes='Остатки линейной регрессионной модели', title_axes_fontsize=16)    
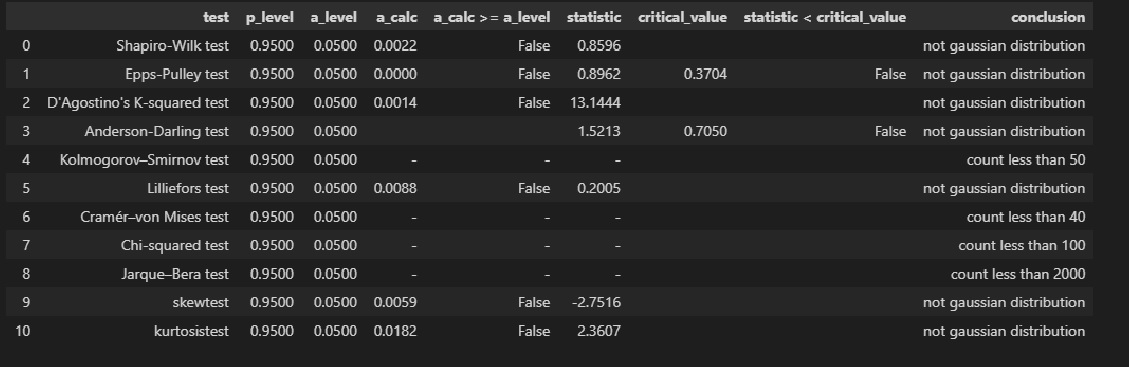
norm_distr_check(res_Y_1)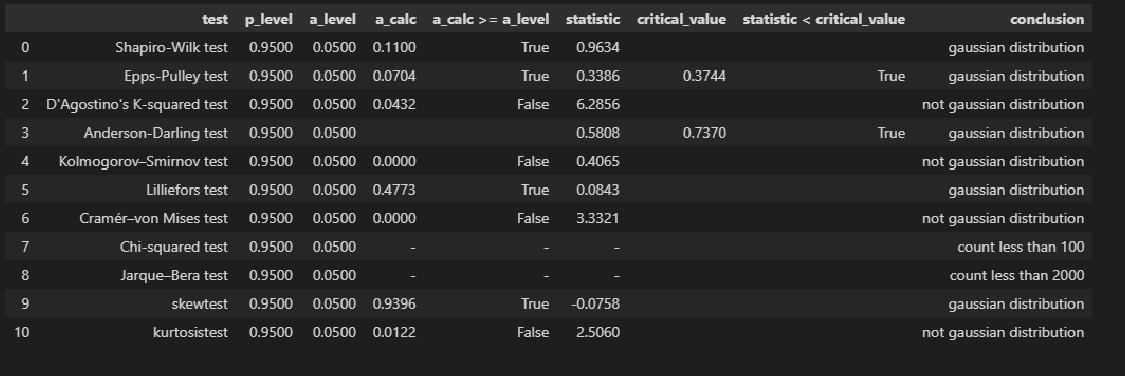

Проверка гетероскедастичности:

Goldfeld_Quandt_test_df = Goldfeld_Quandt_test(result_linear_ols_1, p_level=0.95, model_name='linear_ols') Breush_Pagan_test_df = Breush_Pagan_test(result_linear_ols_1, p_level=0.95, model_name='linear_ols') White_test_df = White_test(result_linear_ols_1, p_level=0.95, model_name='linear_ols')  heteroscedasticity_tests_df = pd.concat([Breush_Pagan_test_df, White_test_df, Goldfeld_Quandt_test_df]) display(heteroscedasticity_tests_df)

Проверка автокорреляции:

sms.stattools.durbin_watson(res_Y_1)

Как видим, результат совпадает со значением статистики критерия в таблице выдачи регрессионного анализа.

display(Durbin_Watson_test(res_Y_1, m=1, p_level=0.95))

Выводы по результатам анализа модели:

Итак, мы провели статистический анализ регрессионной модели и установили:

  1. Регрессионная модель хорошо аппроксимирует фактические данные.

  2. Остатки модели имеют нормальное распределение (хотя результаты тестов противоречивы).

  3. Коэффициент детерминации значим; модель объясняет 97% вариации независимой переменной.

  4. Коэффициенты регрессии значимы.

  5. Обнаружена гетероскедастичность.

  6. Тест критерия Дарбина-Уотсона свидетельствует о наличии значимой положительной автокорреляции остатков.

Резюме — несмотря на вроде бы формально хорошие качественные показатели, нам следует признать эту модель некачественной и отвергнуть по следующим негативным причинам:

  1. На графике модели хорошо заметна точка излома, которая говорит о смене тенденции (существуют специальные статистические тесты для проверки гипотез о смене тенденции, например, тест Чоу, но мы в данном обзоре рассматривать их не будем).

  2. График остатков показывает нам крайне неприглядную картину: на начальном этапе тенденции явно прослеживаются колебания, а после точки излома тенденция вообще кардинально меняется.

  3. Противоречивость тестов проверки нормальности распределения остатков.

  4. Наличие гетероскедастичности.

  5. Наличие автокорреляции. Явление автокорреляции может возникать в случае смены тенденции [5, с.118].

Тот факт, что распределение остатков признается нормальным по результатам таких тестов как Шапиро-Уилка, Эппса-Палли, Андерсона-Дарлинга может иметь разные причины, например, мы можем иметь дело со смесью двух распределений. Этот вопрос требует отдельного тщательного исследования.

Применение построенной модели приведет к ошибке, так как модель хорошо аппроксимирует существующие данные, но из-за смены тенденции неспособна дать качественный прогноз. Проиллюстрировать это можно, построив доверительный интервалы прогноза (формально мы можем это сделать, так как распределение остатков признано нормальным):

graph_regression_pair_predict_plot_sns(     model_fit=result_linear_ols_1,     regression_model_in=regr_model_linear_ols_1_func,     Xmin=X_min_graph, Xmax=X_max_graph+12, Nx=25,     Ymin_graph=2.0, Ymax_graph=Y_max_graph,     title_figure=Variable_Name_Ind_design_2001, title_figure_fontsize=16,     title_axes='Линейная регрессионная модель', title_axes_fontsize=14,     #x_label=Variable_Name_X,     #y_label=Variable_Name_Y,     label_legend_regr_model=f'линейная регрессия Y = {b0:.3f} + {b1:.4f}*X',     s=50,     result_output=False)

Нет, такой прогноз нам не нужен.

ПРИМЕР 2: проверка автокорреляция регрессионной модели

Формирование исходных данных

Рассмотрим пример множественной линейной регрессионной модели, приведенный в источнике [6, с.192].

В качестве исходных данных рассматриваются ряд макроэкономических показателей США за 1960-1985 гг. (в сопоставимых ценах 1982 г., млрд.долл):

  • DPI — годовой совокупный располагаемый личный доход;

  • CONS — годовые совокупные потребительские расходы;

  • ASSETS — финансовые активы населения на начало календарного года.

Предполагается, что между переменной CONS и регрессорами DPI, ASSETS имеется линейная регрессионная связь.

Исходные данные содержаться в файле Macroeconomic_indicators_USA_1960_1985.csv, который помещен в папку data.

Прочитаем csv-файл:

data_df = pd.read_csv(filepath_or_buffer='data/Macroeconomic_indicators_USA_1960_1985.csv', sep=';') display(data_df) #display(data_df.head(), data_df.tail()) data_df.info()

Визуализация

fig, axes = plt.subplots(figsize=(297/INCH, 210/INCH))  title_figure = 'Анализ макроэкономических показателей США за 1960-1985 гг.' fig.suptitle(title_figure, fontsize = 18)  sns.lineplot(     x = data_df['YEAR'], y = data_df['DPI'],     linewidth=3,     legend=True,     label='DPI',     ax=axes)  sns.lineplot(     x = data_df['YEAR'], y = data_df['CONS'],     linewidth=3,     legend=True,     label='CONS',     ax=axes)  sns.lineplot(     x = data_df['YEAR'], y = data_df['ASSETS'],     linewidth=3,     legend=True,     label='ASSETS',     ax=axes)  axes.set_xlabel('Year') axes.set_ylabel('US$ billion')  plt.show()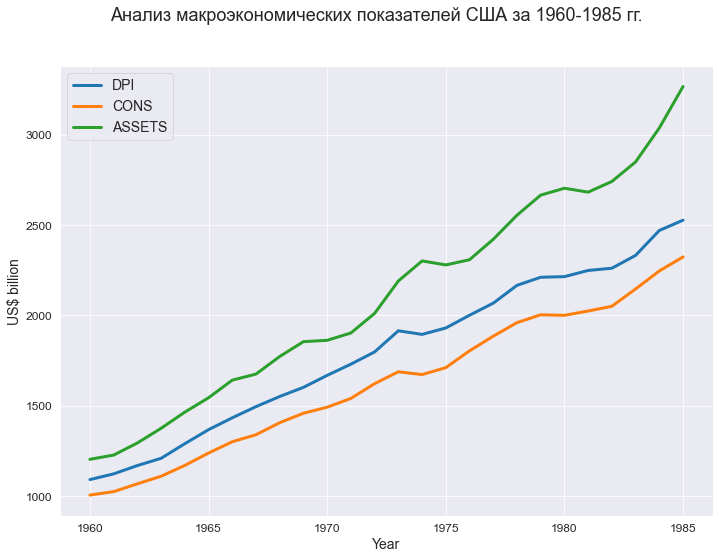

Построение и анализ регрессионной модели

Построим линейную регрессионную модель и проведем ее экспресс-анализ:

y = data_df['CONS'] X = data_df[['DPI', 'ASSETS']] X = sm.add_constant(X) model_linear_ols_2 = sm.OLS(y, X) result_linear_ols_2 = model_linear_ols_2.fit() print(result_linear_ols_2.summary2())

График модели:

fig = plt.figure(figsize=(297/INCH, 420/INCH/1.5)) ax1 = plt.subplot(2,1,1) ax2 = plt.subplot(2,1,2)  title_figure = 'Анализ макроэкономических показателей США за 1960-1985 гг.' fig.suptitle(title_figure, fontsize = 18)  fig = sm.graphics.plot_fit(     result_linear_ols_2, 'DPI',     vlines=True,    # это параметр отвечает за отображение доверительных интервалов для Y     ax=ax1) ax1.set_ylabel('CONS (US$ billion)', fontsize = 12) ax1.set_xlabel('DPI (US$ billion)', fontsize = 12) ax1.set_title('Fitted values vs. DPI', fontsize = 15)  fig = sm.graphics.plot_fit(     result_linear_ols_2, 'ASSETS',     vlines=True,    # это параметр отвечает за отображение доверительных интервалов для Y     ax=ax2) ax2.set_ylabel('CONS (US$ billion)', fontsize = 12) ax2.set_xlabel('ASSETS (US$ billion)', fontsize = 12) ax2.set_title('Fitted values vs. ASSETS', fontsize = 15)  plt.show()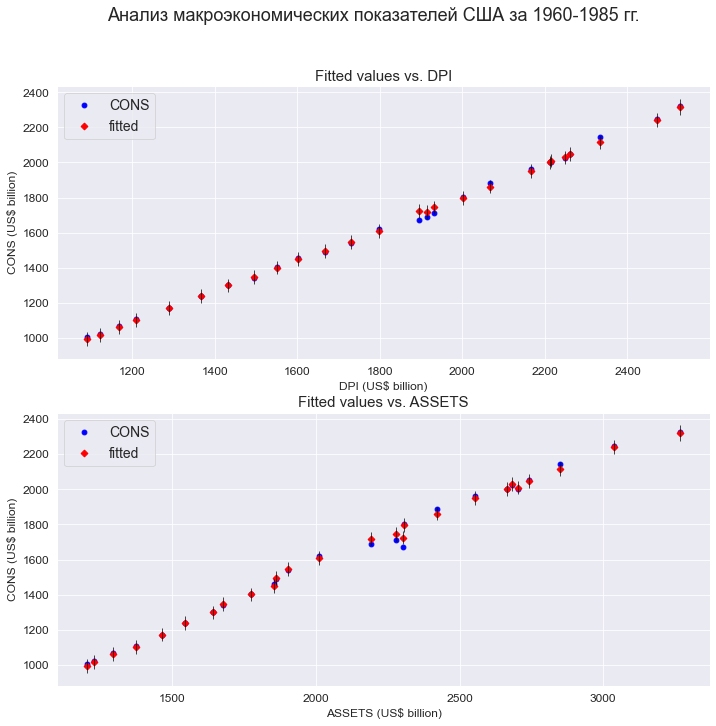

Ошибки аппроксимации модели:

(model_error_metrics, result) = regrpy ession_error_metrics(model_linear_ols_2, model_name='linear_ols') display(result)

Проверка нормальности распределения остатков:

res_Y_2 = np.array(result_linear_ols_2.resid)  # Пользовательская функция graph_hist_boxplot_probplot_sns(     data=res_Y_2,     data_min=-60, data_max=60,     graph_inclusion='hbp',     data_label=r'$ΔY = Y - Y_{calc}$',     #title_figure=Task_Project,     title_axes='Остатки линейной регрессионной модели', title_axes_fontsize=16)      norm_distr_check(res_Y_2)

Прроверка гетероскедастичности:

Goldfeld_Quandt_test_df = Goldfeld_Quandt_test(result_linear_ols_2, p_level=0.95, model_name='linear_ols') Breush_Pagan_test_df = Breush_Pagan_test(result_linear_ols_2, p_level=0.95, model_name='linear_ols') White_test_df = White_test(result_linear_ols_2, p_level=0.95, model_name='linear_ols')  heteroscedasticity_tests_df = pd.concat([Breush_Pagan_test_df, White_test_df, Goldfeld_Quandt_test_df]) display(heteroscedasticity_tests_df)

Проверка автокорреляции:

display(Durbin_Watson_test(res_Y_2, m=1, p_level=0.95))

Выводы по результатам анализа модели:

Как видим, в целом результаты расчетов совпадают с результатами из первоисточника [6], в части выявления автокорреляции аналогично.

Информация к размышлению.

Анализ показывает, что модель хорошо аппроксимирует фактические данные, но имеет место отклонение от нормального закона распределения остатков, противоречивые выводы о гетероскедастичности и наличие автокорреляции, то есть модель некачественная.

Также мы видим, что динамика макроэкономических показателей свидетельствует о наличии трендов, однако, если в модель добавить еще один фактор — год или номер наблюдения — то, этот фактор окажется незначимым.

В дальнейшем автор при анализе остатков модели [6, с.198] выявляет структурный сдвиг (обусловленный мировым топливно-энергетическим кризисом в 1973 г.) и вводит в модель фиктивные переменные, учитывающие этот структурный сдвиг

ИТОГИ

Итак, подведем итоги:

  • мы рассмотрели способы реализации в полной мере критерия Дарбина-Уотсона средствами python, создали пользовательскую функцию, уменьшающую размер кода;

  • разобрали пример оцифровки таблицы критических значений статистического критерия для реализации пользовательской функции.

Исходный код находится в моем репозитории на GitHub (https://github.com/AANazarov/Statistical-methods).

Надеюсь, данный обзор поможет специалистам DataScience в работе.

ЛИТЕРАТУРА

  1. Кобзарь А.И. Прикладная математическая статистика. Для инженеров и научных работников. — М.: ФИЗМАТЛИТ, 2006. — 816 с.

  2. Айвазян С.А. Прикладная статистика. Основы эконометрики: В 2 т. — Т.2: Основы эконометрики. — 2-е изд., испр. — М.: ЮНИТИ-ДАНА, 2001. — 432 с.

  3. Фёрстер Э., Рёнц Б. Методы корреляционного и регрессионного анализа / пер с нем. — М.: Финансы и статистика, 1983. — 302 с.

  4. Магнус Я.Р. и др. Эконометрика. Начальный курс — М.: Дело, 2004. — 576 с.

  5. Тихомиров Н.П., дорохина Е.Ю. Эконометрика. — М.: Экзамен, 2003. — 512 с.

  6. Носко В.П. Эконометрика. Кн.1. Ч.1, 2. — М.: Издательский дом «Дело» РАНХиГС, 2011. — 672 с.

  7. Вандер Плас Дж. Python для сложных задач: наука о данных и машинное обучение. — СПб: Питер, 2018. — 576 с.


ссылка на оригинал статьи https://habr.com/ru/post/693402/

Комментарии

Добавить комментарий

Ваш адрес email не будет опубликован. Обязательные поля помечены *