Салют, Хабр! Построение нейронной сети ― весьма актуальная задача для самых разных направлений: от классификации продуктов на категории до распознавания лиц на видео. Однако для получения качественного результата необходимо грамотно настроить её параметры. Как это сделать? В этом может помочь Keras ― открытая библиотека, написанная на языке Python и обеспечивающая взаимодействие с искусственными нейронными сетями. Просим под кат, где подробно рассказываем о нюансах работы с этой библиотекой.
Зачем эта статья?
Наша команда решила поделиться опытом построения нейронной сети и регулирования её гиперпараметров с помощью Keras. Рассказываем и показываем практически.
Анализ, о котором говорится ниже, мы провели на примере открытого датасета из Kaggle Otto group product classification challenge. Количество строк в нём составляет примерно 62 тысячи. Каждая строка соответствует одному продукту. Необходимо классифицировать продукты компании по девяти категориям, основываясь на 93 характеристиках. Каждая категория ― это тип продукта, например мода, электроника и т. д. Классы не сбалансированы, что можно увидеть на графике.

Описательные статистики для переменных:

В статье шаг за шагом разбираем логические блоки для построения модели: входные данные, слои, количество нейронов, функция активации, процедура обучения.
Как это сделано?
Что же, приступим. Для начала импортируем необходимые библиотеки:
from tensorflow.keras.models import Sequential from tensorflow.keras.layers import Dense, Dropout, Activation, Flatten from tensorflow.keras.optimizers import Adam,SGD,Adagrad from tensorflow.keras.wrappers.scikit_learn import KerasClassifier from tensorflow.keras.initializers import glorot_uniformНа вход нейронной сети подаются тензоры. Это общая форма векторов в виде n-мерной матрицы. Если данные табличные (как в данном случае), то тензор будет двумерный, где каждый столбец этой матрицы ― это одно наблюдение из таблицы (одна строка табличных данных).
y = x.target.values x.drop('target', axis=1, inplace=True) x = np.log(1+x.values)Общая структура сети разрабатывается с помощью объекта модели keras Sequential(), который создаёт последовательную модель с пошаговым добавлением слоёв в неё. Dense-слой является самым необходимым и базовым. Он отвечает за соединение нейронов из предыдущего и следующего слоя. Например, если первый слой имеет 5 нейронов, а второй 3, то общее количество соединений между слоями будет равно 15. Dense-слой отвечает за эти соединения, и у него есть настраиваемые гиперпараметры: количество нейронов, тип активации, инициализация типа ядра. Dropout Layer помогает избавиться от переобучения модели. Таким образом, некоторые нейроны становятся равными 0, и это сокращает вычисления в процессе обучения. Базовая модель представлена ниже:
def getModel(dropout=0.00, neurons_first=500, neurons_second=250, learningRate=0.1): model = Sequential() model.add(Dense(neurons_first, activation='relu', input_dim=num_features, kernel_initializer=glorot_uniform(), name='Dense_first')) model.add(Dropout(dropout, name='Dropout_first')) model.add(Dense(neurons_second, activation='relu', kernel_initializer=glorot_uniform(), name='Dense_second')) model.add(Dropout(dropout, name='Dropout_second')) model.add(Dense(num_classes, activation='softmax', kernel_initializer=glorot_uniform(), name='Result')) model.compile(loss='sparse_categorical_crossentropy', optimizer=Adagrad(lr=learningRate), metrics=['accuracy']) return modelТеперь давайте разберёмся с тем, что собой представляет функция активации. Так вот, каждый нейрон сети получает один или несколько входных сигналов от нейронов предыдущего слоя. Если речь идёт про первый скрытый слой, то он получает данные из входного потока. Начиная со второго скрытого слоя, на вход каждому нейрону подаётся взвешенная сумма нейронов из предыдущего слоя. На втором скрытом слое происходит активация входных данных за счёт функции активации. С помощью функции активации становится доступной реализация обратного распространения ошибки, которая помогает скорректировать веса нейронов. Таким образом происходит обучение модели. Важный момент ― существует несколько вариантов функции активации.
Для текущей задачи использовались функции активации ReLu и Softmax. Функция ReLu выглядит следующим образом:

Функция Softmax выглядит следующим образом:
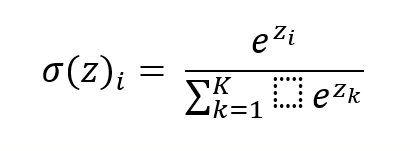
Функция потерь ― показатель, который помогает понять, движется ли сеть в правильном направлении. Так как задача решается для многоклассовой классификации, то использовалась функция потерь sparse categorical crossentropy:
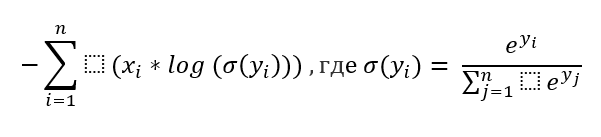
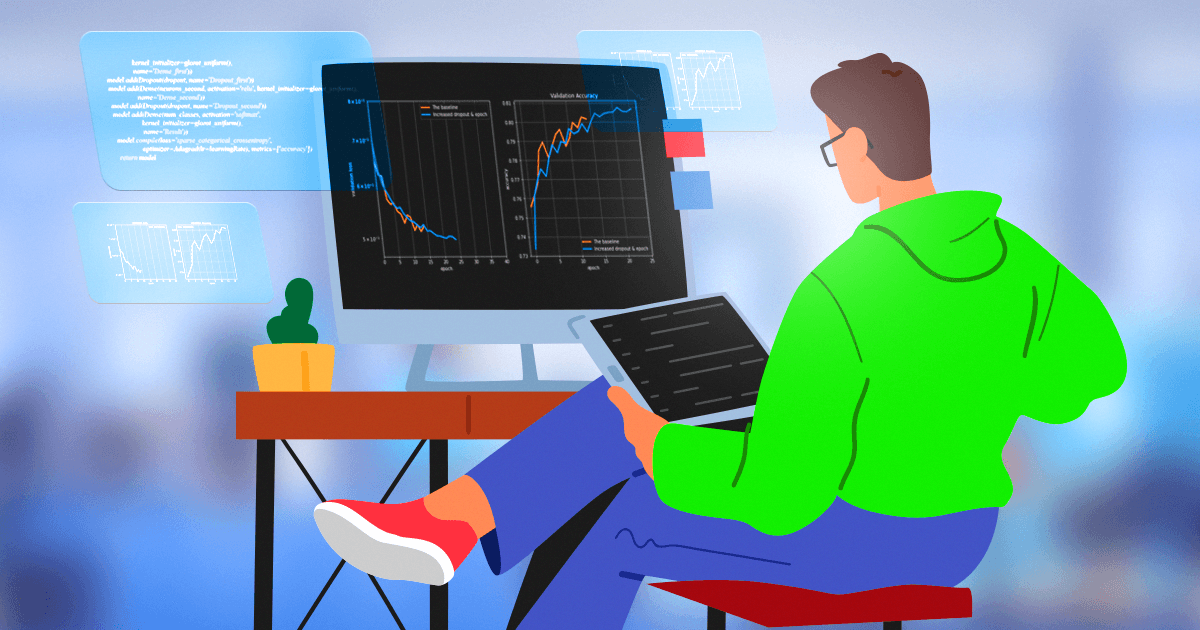
Посмотрим теперь на качество модели с параметрами, заданными ранее. Ниже ― график, на котором изображена функция потерь и точность нашего классификатора. Видим, что наилучший результат наблюдается около 13-й эпохи, однако видно переобучение модели из-за большой флуктуации функции потерь.

Что ещё?
Наиболее важной частью обучения модели является оптимизатор. Ранее был упомянут термин обратного распространения ошибки ― это как раз и есть процесс оптимизации. Структура, которая ранее была описана, инициализируется случайными весами между нейронами слоёв. Процесс обучения нужен для того, чтобы обновить эти случайные веса для получения высокой предсказательной способности.
Сеть берёт одну обучающую выборку и использует её значения в качестве входных данных слоя, далее происходит активация этих данных, и на вход следующему слою подаются уже новые взвешенные данные после активации. Аналогичный процесс происходит и на последующих слоях. Результат последнего слоя будет прогнозом для обучающей выборки. Далее применяется функция потерь, которая показывает, насколько сильно ошибается модель. Чтобы эту ошибку уменьшить, применяется ещё одна функция ― оптимизатора. Она использует производные для ответа на вопрос ― насколько сильно изменится функция потерь при небольшом изменении весов между нейронами?
Вычисление одной обучающей выборки из входного слоя называется проходом. Обычно обучение происходит батчами из-за ограничений системы. Батч ― набор обучающих выборок из входных данных. Сеть обновляет свои веса после обработки всех выборок из батча. Это называется итерацией (то есть успешная обработка всех обучающих выборок из батча с последующим обновлением весов в сети). А вычисление всех обучающих выборок, которые были во входных данных, с периодическими обновлениями весов называется эпохой. На каждой итерации сеть использует функцию оптимизации, чтобы внести изменения в веса между нейронами. Шаг за шагом, с помощью нескольких итераций, а затем нескольких эпох, сеть обновляет свои веса и учится делать корректный прогноз. Существует много разных функций оптимизации. В нашем случае была использована Adagrad.
Оптимизируем всё!
Ну а теперь давайте попробуем улучшить качество модели. Здесь пригодится увеличение dropout rate. То есть теперь больше нейронов будут выходить из процесса обучения.
increasedDropout = 0.5 model = getModel(increasedDropout) net = model.fit(X, y, epochs=15, batch_size=515, verbose=1, validation_split=0.2)На графике видно, что проблемы переобучения больше нет, так как функция потерь стала более гладкой.

Увеличение количества эпох.
model = getModel(increasedDropout) net = model.fit(X, y, epochs=25, batch_size=515, verbose=1, validation_split=0.2)Заметно, что качество улучшилось. Задача выполнена, и сделали мы это весьма неплохо, правда?

Увеличение количества нейронов.
increasedNeurons1 = 800 model = getModel(increasedDropout, neurons_first=increasedNeurons1) net = model.fit(X, y, epochs=25, batch_size=515, verbose=1, validation_split=0.2)Качество модели стало ещё лучше.

Был взят небольшой объём данных, чтобы показать прогноз модели. Из результатов видно, что ошибка модели невелика.

Как и говорилось выше, чаще всего встречаются классы 2 и 6. Соответственно, модель меньше всего ошибается именно в них.
В сухом остатке
Мы смогли избавить модель от переобучения путём увеличения dropout, после чего более высокие результаты были достигнуты за счёт увеличения количества нейронов и эпох. В конечном счёте общая точность предсказания модели по всем классам продуктов составляет чуть больше 0,81, что характеризует её качество. Соответственно, теперь эту модель можно использовать для решения задачи многоклассовой классификации. Плюс в том, что структура является универсальной, так что её можно использовать при решении задач с применением нейронных сетей.
ссылка на оригинал статьи https://habr.com/ru/company/sberbank/blog/695588/
Добавить комментарий