
Перед вами AGI лонгрид, друзья, много картинок и гифок. Обещанная в прошлой статье практическая часть тоже будет.
К AGI через моделирование объектов реального мира
Вы когда-нибудь задумывались над тем, возможно ли в принципе смоделировать жизнь (и человека, в частности) на компьютере? Большинство исследователей, которые задавали себе этот вопрос, ответят на него положительно.
И тут важно понять, чем и насколько модель мира должна отличаться от мира, чтобы мы ответили да. Minecraft — модель реального мира? Очевидно же, что да. Точная? Очевидно, что нет.
Но есть более интересный вопрос: Можно ли через моделирование объектов реального мира сделать AGI (что бы оно ни значило)? С первого взгляда кажется, что да, можно, ведь на компьютере можно смоделировать что угодно, с какой угодно точностью.
Изучаем, с помощью эксперимента, как происходит взаимодействие между Нейроном и какой-нибудь Глией в реальности, потом просто кодим это на компе, отличный план! В итоге получим высокоточную модель кортикальной колонки мозга мыши.
Модель колонки мы получим, тут нет сомнений. А вот получим ли мы таким образом кирпичик AGI (несмотря на то, что мы к этому не стремились) — тут большоой вопрос.

Что такое Джоуль?
Рассмотрим подход к созданию AGI, основанный на принципах экономии/оптимизации/минимизации собственной/внутренней/затраченной энергии. Подход с оптимизацией по энергии не вызывает отторжения, и всё потому что, помимо математики, мы верим также и в физику. У системы есть желание прийти в состояние с меньшим/большим количеством энергии, либо среди всех возможных вариантов выбрать ход с минимальными/максимальными энергетическими/временными затратами. Я не настоящий физик, термодинамику изучал довольно давно, поэтому могу быть неточен, выберите свой вариант по вкусу, суть в другом.
На вопрос «Как планируется моделировать Джоуль?» ответа, как правило, не поступает. И тут, на самом деле, не только про Джоуль, а про любые физические величины, по которым предлагается оптимизироваться: будь-то метры с канделами, либо, внезапно, удовольствие с болью, имеющие числовое значение. Люди просто не думают об этом.
Вам, разумеется, покажется, что я пишу очевиднейший и лютейший бред насчёт Джоулей, Килограммов и прочих числовых характеристик объектов реального мира. Ведь, очевидно же, чтоб что-либо смоделировать, нам надо разобраться как оно работает, понять его поведение и взаимодействие с другими объектами, набить его переменными и константами. А какую-нибудь «Скорость истечения ионов Калия через мембрану, ед. в секунду» не требуется моделировать! Достаточно правильно привязаться к области памяти длиной 64 бита, т.е. числу двойной точности (double), переменной, используемой для меры в расчётах.
Еще пример. Программистам очевидно, что у класса Car может быть поле double power, а различные объекты этого класса — т.е. конкретные марки автомобилей, могут различаться по мощности мотора. Если в модели автомобиля потребуется указать единицу измерения мощности, мы можем положить её рядом с вещественным полем, дополнительным атрибутом. Проблема решена!
Можно долго объяснять, приводить примеры… но я надеюсь на вашу способность ухватывать суть. В конце концов оказывается, что любое сколь угодно сложное поведение моделей сводится к операциям с символами-числами, лежащими внутри них.
В моделях мы используем статистически выявленные закономерности реального мира. В моделях используются меры множеств объектов. Если объектов много, и считать их трудоёмко, мы можем количество объектов отобразить на шкалу. С некоторой единицей измерения, скажем, Ваттом.
Вот так и получается, что поведение реальных ионов Калия, проникающих через мембрану в огромных количествах, заменяются на бездушное вещественное число. Понимаете, да? Были объекты реального мира (ионы), а стало одно-единственное вещественное число, абстрактное в силу своей числовой природы. Да-да, ионов много, а в среднем их поведение неплохо описывается простой функциональной зависимостью, совершенно незачем расходовать лишние ресурсы, чтобы в итоге заведомо получить одно и то же!
Я изобрёл вечный двигатель
И вот тут к нам приходит исследователь, и говорит: «Я изобрёл AGI — тестируйте!».
В чём же заключаются «две большие разницы» между моделью мира на компьютере и миром в реальности? И как понимание этих разниц может помочь в тестировании алгоритмов формата AGI / not_AGI?
Если заявляемый алгоритм AGI использует числа — это не значит, что алгоритм не является AGI. Не нужно сразу банить бедного учёного. Это лишь означает, что используемые символьные вычисления не участвуют в core логике тестируемого AGI.

Вдумчиво и последовательно нужно разобрать предлагаемый AGI алгоритм на составляющие, убирая при этом символьные вычисления. Оставшаяся логика и будет определять заявляемый AGI функционал. Ну а дальше уже нужно смотреть предметно и испытывать core логику с помощью других тестов.
Очевидно, вам хотелось бы пример core логики, которая бы проходила этот тест. Пожалуйста: в общем случае — детерминированный конечный автомат. В частности, и по-простому — какой-нибудь хардкод, использующий категориальные свойства объектов.
Отлично, одно из необходимых условий для AGI мы уяснили. Идём дальше. Разберёмся, с фрактальными свойствами реального мира и, далее, со способами их реализации в алгоритме AGI.
Фрактальные свойства систем с человеком внутри и человеком снаружи
У. Росс Эшби в середине прошлого века предположил (и я полностью разделяю его взгляды), что регулятор может быть создан только другим регулятором, либо выбран в результате отбора из некоего множества регуляторов.
В том, что человек является примером системы, способной быть регулятором, а также создавать регуляторы, сомневаться не приходится. Элементарный пример: человек управляет полётом самолёта и синтезированный человеком автопилот способен на часть такого поведения.
А в чём разница, когда самолётом управляет автопилот и и человек? Ответ на поверхности, и уже озвучен — современные автопилоты способны лишь на часть способностей человека. Автопилот ведь не решит вдруг выполнять групповые фигуры пилотажа, посовещавшись с другими автопилотами!
Самолёт является расширением возможностей для человека. Это свойство — перманентное усложнение поведения системы, если внутри неё есть человек, характерно для всех частей нашего фрактального мира. Семейные ценности становятся всё многограннее, государственные законы всё противоречивее.
Фрактал — это, по определению, некое множество, обладающее свойствами самоподобия.
Давайте гипотетически представим, что наш мир — это фрактал, и попробуем найти сходство между различными частями этого фрактала. Соответствие будем искать не только в форме, как вы, возможно, подумали, а еще и в правилах функционирования частей. И ограничимся лишь системами с человеком внутри (или, хм, с человеком снаружи).
Какие части будем анализировать? А вот такие, по мере усложнения: нейрон, печень, человек, общество с ограниченной ответственностью, город, государство, организация объединённых наций.
И окажется, что есть очень простое общее свойство поведения долгоживущих систем на любом уровне мировой фрактальной иерархии.
Что нужно делать, чтобы выжить в системе как можно дольше?
Придерживаться правил)
Чтобы автомобилю выжить среди автомобилей на дороге нужно придерживаться ПДД. Чтобы арестанту выжить в тюрьме, нужно придерживаться правил внутреннего распорядка тюрьмы. Чтобы нейрону выжить в мозге, надо придерживаться правил Хебба (или любой ваш вариант). Чтобы печени выжить внутри человека, ей тоже приходится выполнять свои функции, иначе говоря, придерживаться правил. Чтобы ООО выжить в государстве, нужно придерживаться целой кучи юридических правил.
Что значит «придерживаться правил»? Давайте приземлим терминологию. Придерживаться правил — это означает демонстрировать поведение, которое ожидается в конкретной ситуации. Это означает, что внешняя среда, в которой живёт агент, не будет никак влиять, точнее, корректировать действия агента, которые он совершает. Вместе, агент и среда, будут действовать согласованным образом. Именно об этом я говорил в прошлой статье, и именно об этом говорит Эшби, когда «синтезирует регуляторы с помощью других регуляторов».
А что значит демонстрировать поведение, которое ожидается? Теперь уже можно конкретизироваться до уровня задачи. Вперёд!
Моделирование чёрного ящика
Широко известная задача, и, пока что, решённая не самым оптимальным образом и далеко не для всех сценариев. В ней исследователю необходимо составить модель неизвестного устройства, чтобы иметь возможность управлять им. Основные проблемы связываются с нечисловой природой входящих/выходящих данных и наличием памяти в ящике.
Большой обзор Анализ и синтез автоматов по их поведению, если кому интересно, что думает современная наука по этому поводу.

Задача моделирования чёрного ящика «о двух концах». С одной стороны, мы пытаемся смоделировать, т.е. скопировать поведение неизвестного устройства, скрытого в ящике. С другой стороны, если ящик «вывернуть наизнанку», мы можем потребовать, чтобы неизвестное устройство подстроилось под внешние сигналы, т.е. научилось управлять поведением известного устройства.
Чувствуете, в чём теперь «интересность» задачи, если немного дополнить её постановку — «Как смоделировать устройство, способное моделировать другие устройства»?
Как управлять чёрным ящиком, если он в это же время управляет вами?

Посмотрим внимательно на рисунок с фрактальным мироустройством из прошлой статьи. Каждый «кружочек» на рисунке — это фрактальная самоорганизующаяся сеть. И каждому кружочку нужно подстроиться под соседей, чтобы сохранить себя как целое.
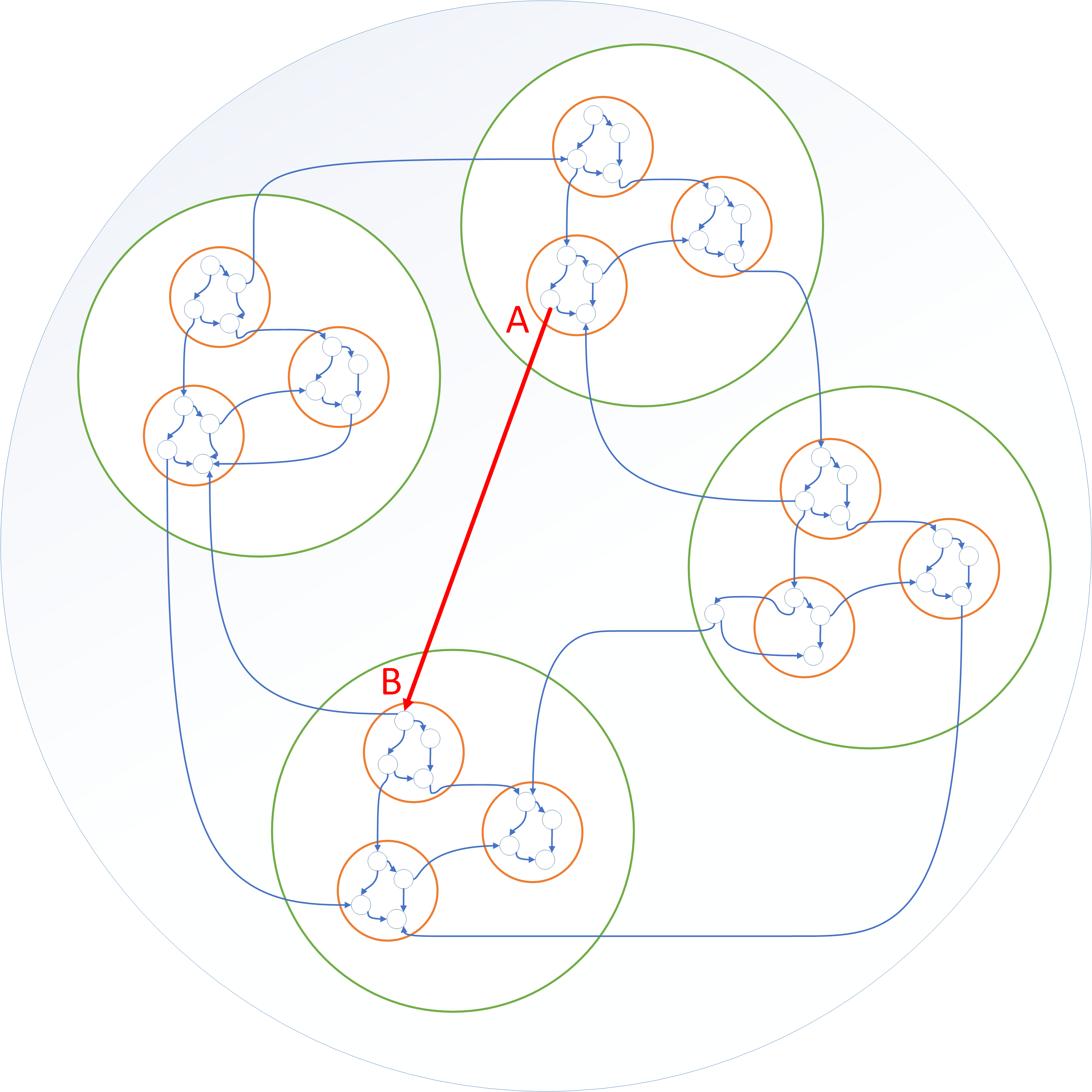
Без каких-либо сомнений, мы можем также сказать, что каждый кружочек — это чёрный ящик, который загадочным образом умеет подстраиваться под своих соседей, таких же чёрных ящиков.
Задача подстройки зелёных чёрных ящиков под им подобных, т.е. задача выживания — это, на самом деле, лишь многократно усложнённое поведение самых мелких элементов (тех, которые внутри оранжевых). Скажу страшную вещь, но интеллект — это лишь свойство достаточно большой группы атомов, правильным образом структурированных.
Пока мы никак не ограничивали способ подстройки чёрного ящика. Это могло быть что угодно, хоть справочник с полной историей сэмплов обучения нашего ящика и хитрый механизм генерализации поверх него. Но теперь понятно, что внутренняя структура ящика работает по абсолютно таким же правилам, что и сам ящик. Внутри ящика — фрактал!
Нам осталось совсем чуть чуть, чтобы перейти в конкретику — нужно реализовать абстрактное правило «Чтобы выжить в системе как можно дольше, нужно придерживаться правил» в конкретном объекте — носителе этих правил. Многие экземпляры (инстансы) таких объектов, выпущенные в некое пространство и будут определять самоорганизующуюся динамику созданного мира.
«Придерживаться правил», «демонстрировать поведение» — это снова задача чёрного ящика.
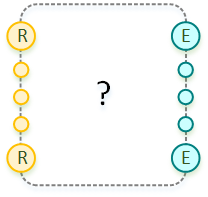
Узлы слева — входящие, отрабатывают любой (нами заданный) предикат. Справа — выходящие, способные воздействовать на среду по сигналу (boolean, да/нет) от сети. Чёрный ящик работает в дискретном времени.
Предикат на входе во входящий узел отфильтровывает лишнее, узел реагирует только на заданное нами внешнее обстоятельство. На выходе из предиката булевское значение, которое интерпретируется стандартным образом — произошла ли конкретная ситуация, случилось ли специфическое событие — да/нет.
Еще раз, «демонстрировать поведение» — означает, что на выходе ящика должны быть выставлены состояния, соответствующие ожиданиям сети, конкретнее, дочерних узлов для данных выходных узлов. Это просто широко известная парадигма обучения с учителем, т.е. мы просто выставляем на выходе устройства желаемые состояния вместе с текущим состоянием входов.
И еще раз — у чёрного ящика нет никакой цели подстроится под соседей! Само существование (наличие) чёрного ящика говорит о том, что внутри него уже реализован механизм подстройки под соседей. Уверен, понимание этого простого факта придёт быстро, если начать смотреть на процессы в динамике, а не в статике. Ну и, разумеется, не нужно забывать, что перед нами фрактал.
Самоорганизующаяся структурно адаптивная сеть
Начнём с того, что попробуем построить какую-нибудь простенькую сеть, чтобы восстановить понимание происходящего, если лень пересматривать Статью раз и Статью два.

Что и как происходит, кратко: изначально в сети нет ничего кроме входящих узлов (представлены жёлтым). Через эти узлы на сеть поступает дискретный поток булевских данных, на каждый такт создаётся новый узел. Сеть увеличивается в размере — растёт.
Правила работы сети
Были первоначально описаны в этой статье. Правила связывания нового узла заданы строго, в них происходит анализ состояние узлов и связей. По сравнению первоначальным вариантом, правила претерпели незначительное изменения, причём, с хорошими последствиями. Обсудим правила связывания ниже.
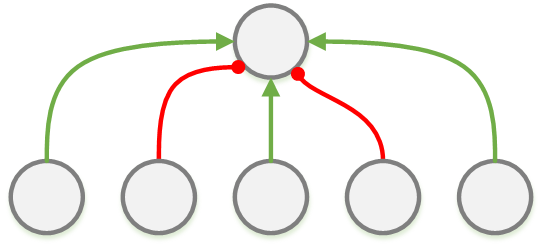
Положительные связи (зелёные) определяют отношение между совместными событиями. При этом направление связи естественным образом задаёт очерёдность наблюдения событий (причинность). Отрицательные связи между узлами можно описать как несовместные события.
Вот так узлы ведут себя в рантайме, когда по ним ходит поток.
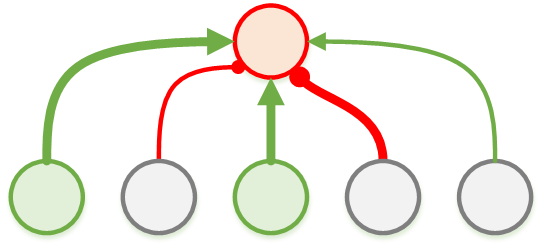
Положительная связь сохраняет свой поток, если он был заблокирован потоком с отрицательной связи, и переносит его на следующий такт глобального дискретного времени.
Случайный поток
Нам важно увидеть, что будет с сетью, если подавать на неё случайный поток данных. Пусть будет 10 входных узлов, непринципиально. Смотрим.

Неслучайный поток
А какова будет динамика внутри сети, если она увидит идущие подряд 30 одинаковых паттернов?
Давайте попробуем провести такой эксперимент на простеньком потоке, чтобы быстрее увидеть интересующую нас динамику. Итак, паттерн будет длительностью всего лишь 6 тактов. Число входящих узлов не сильно важно сейчас. Смотрим на начальный этап:

Через какое-то время, когда сеть подрастёт, мы заметим, что:
-
по сети «гуляет» повторяющийся паттерн активности узлов;
-
сеть странным образом имеет структуру с похожими участками;
-
сеть имеет вытянутую форму.
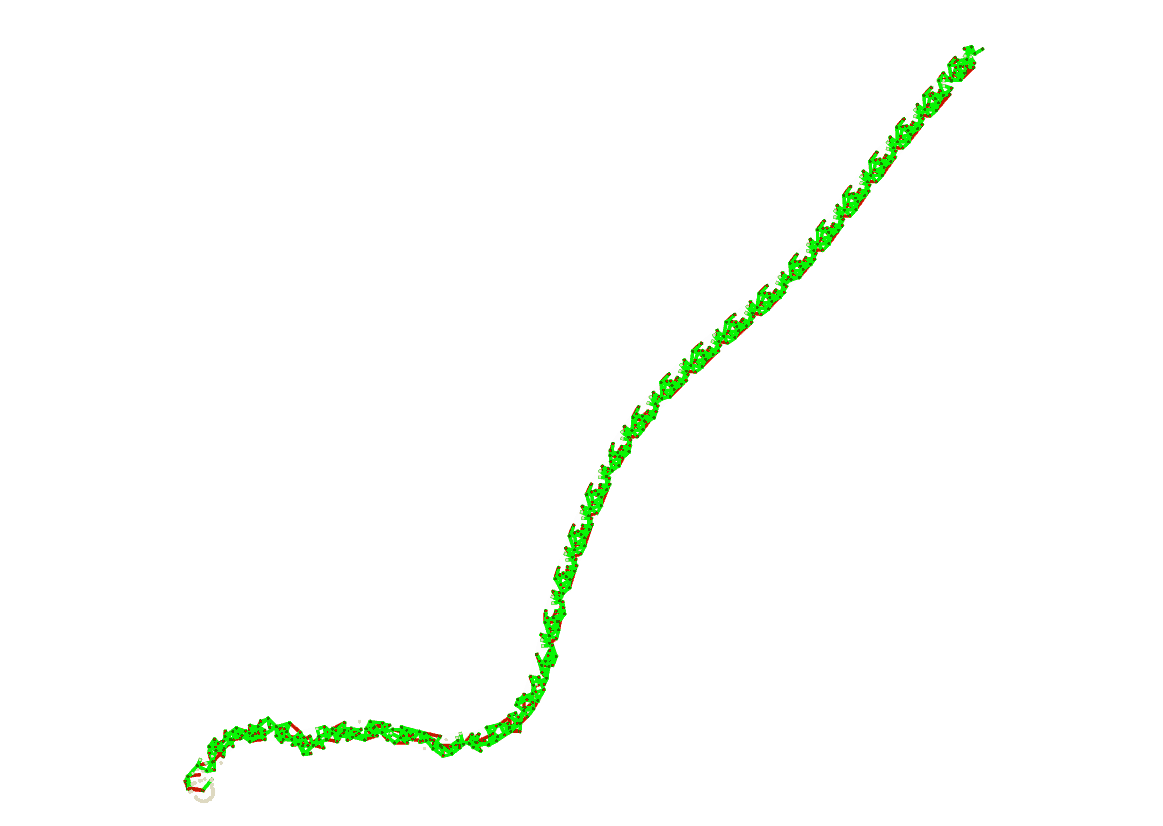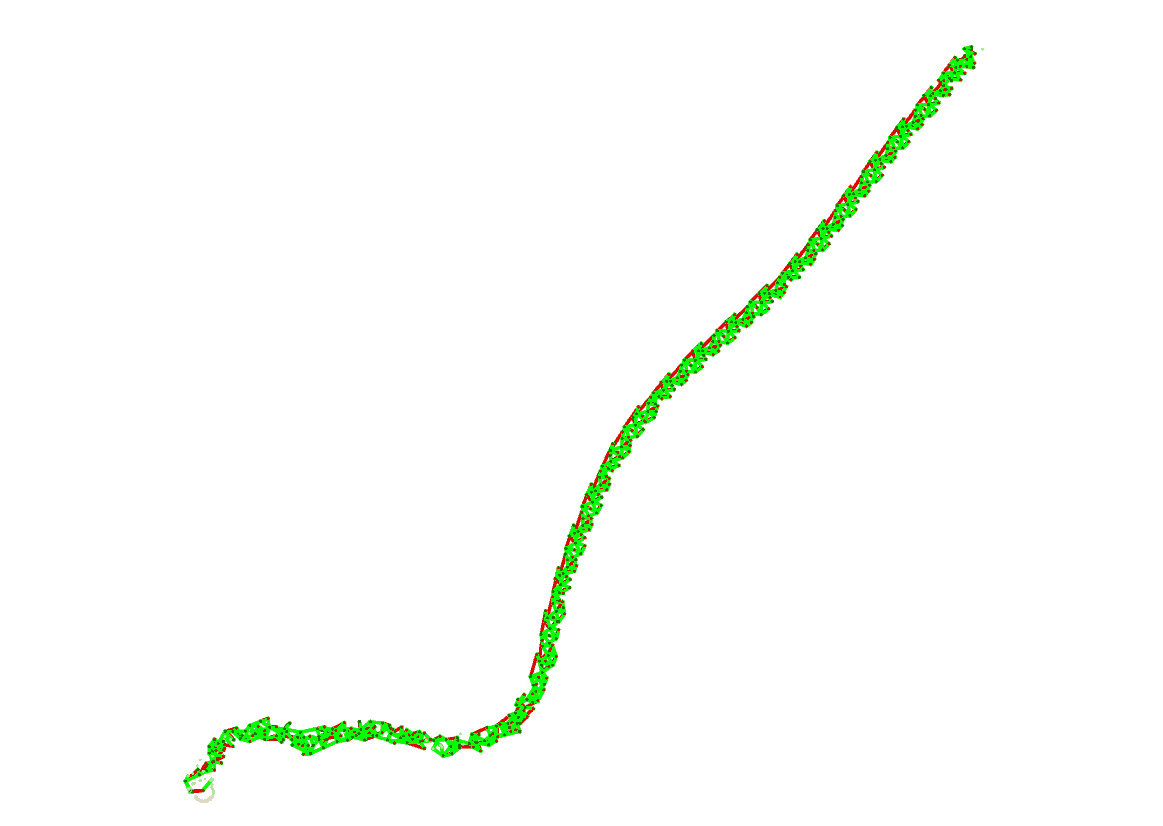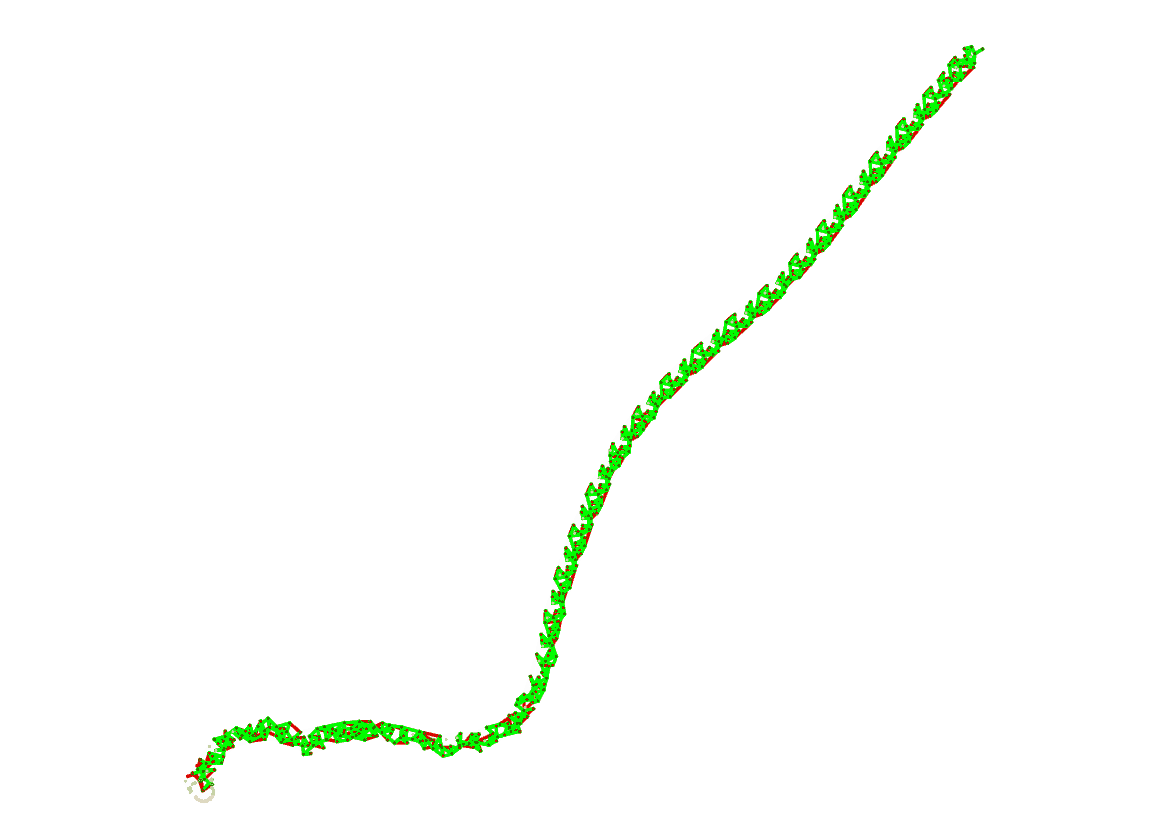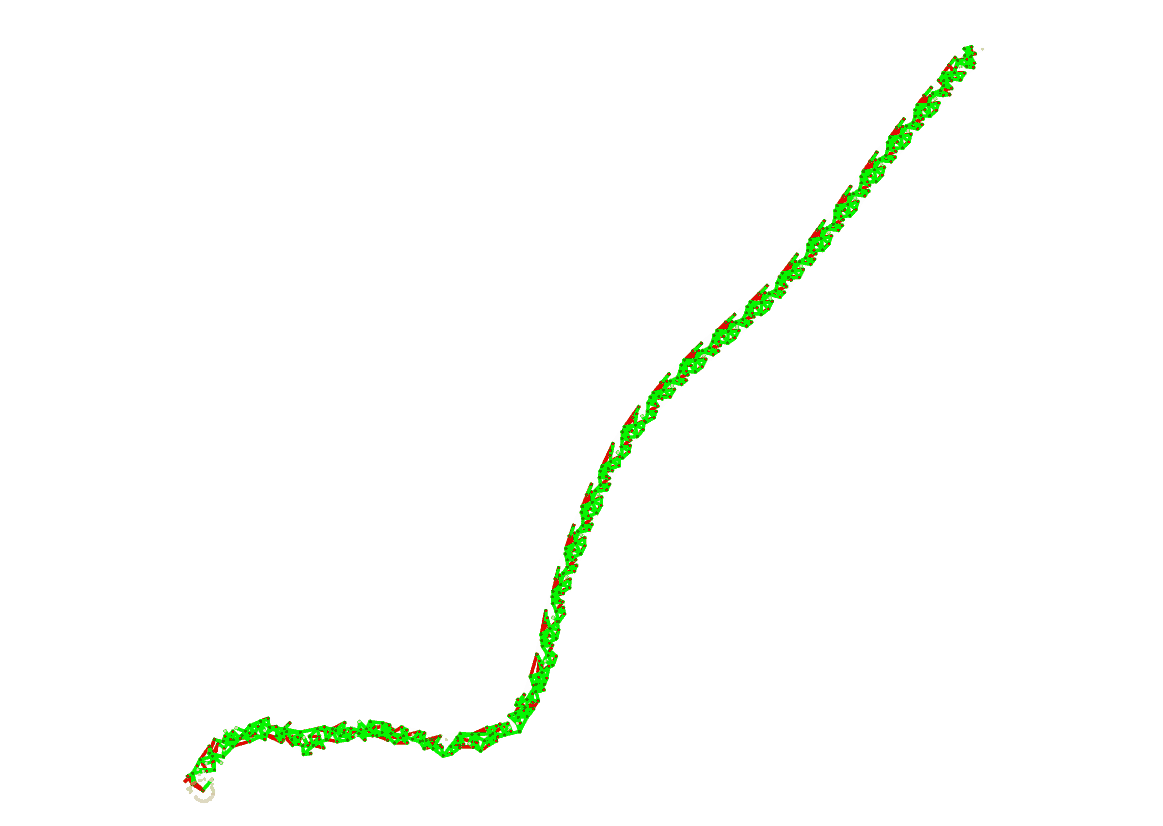
Преобразование потока данных в структуру — взаимно однозначное. Подача разных потоков данных всегда приводит к разным структурам сети на выходе. Ну ладно, запомнили. Попробуем поискать другие полезные свойства сети.
Распознавание последовательностей (последовательностей)
Чтобы было удобнее отслеживать динамику состояния сети мы будем использовать стандартное средство — щуп. Направим его в некоторую область внутри сети, снимем состояния узлов в каждом такте и возьмём простую хэш-функцию от этой совокупности состояний.
Снова подадим повторяющийся паттерн. Паттерн будет длиной 20 тактов, что непринципиально, лишь бы уместился на ширине окна нашего виртуального осциллографа.
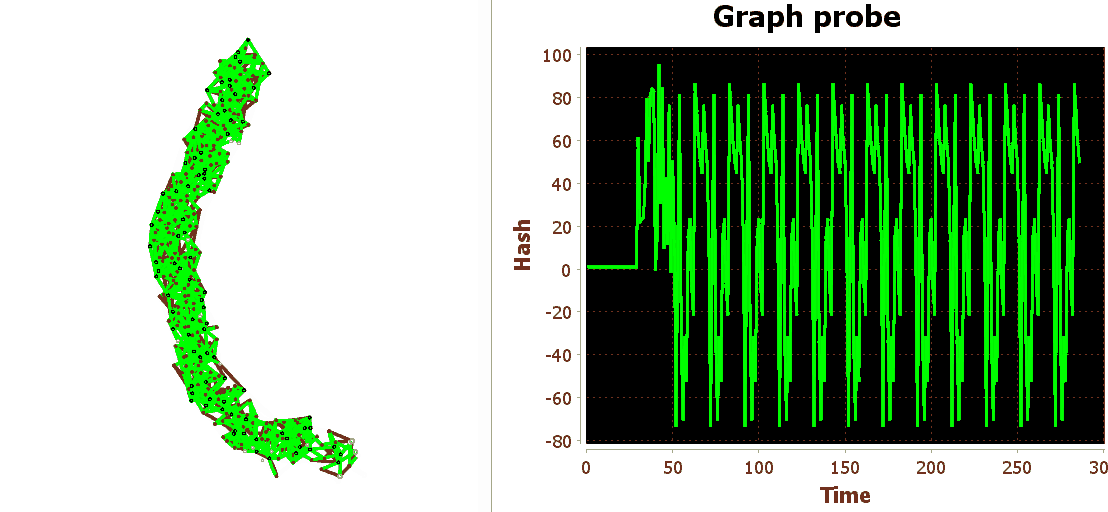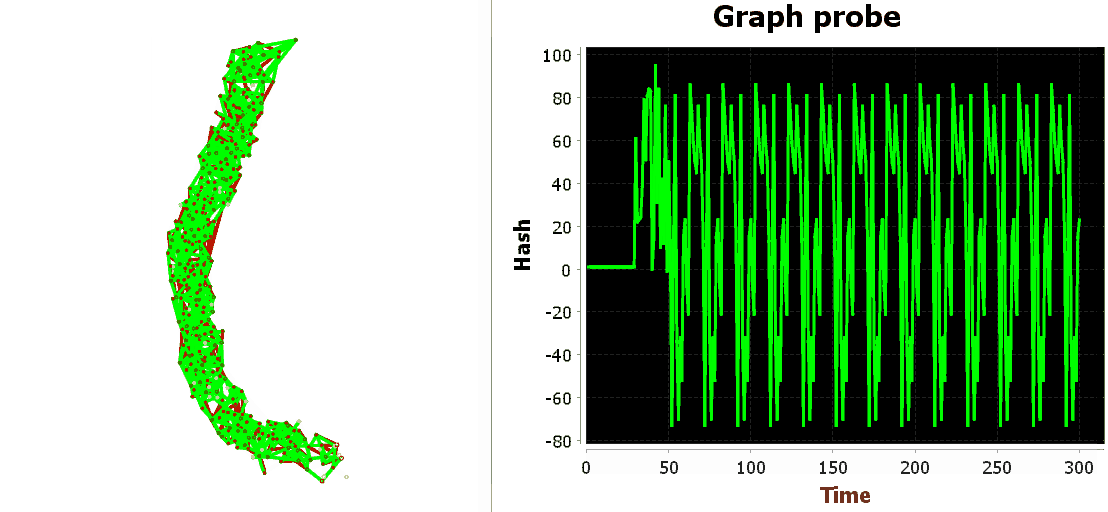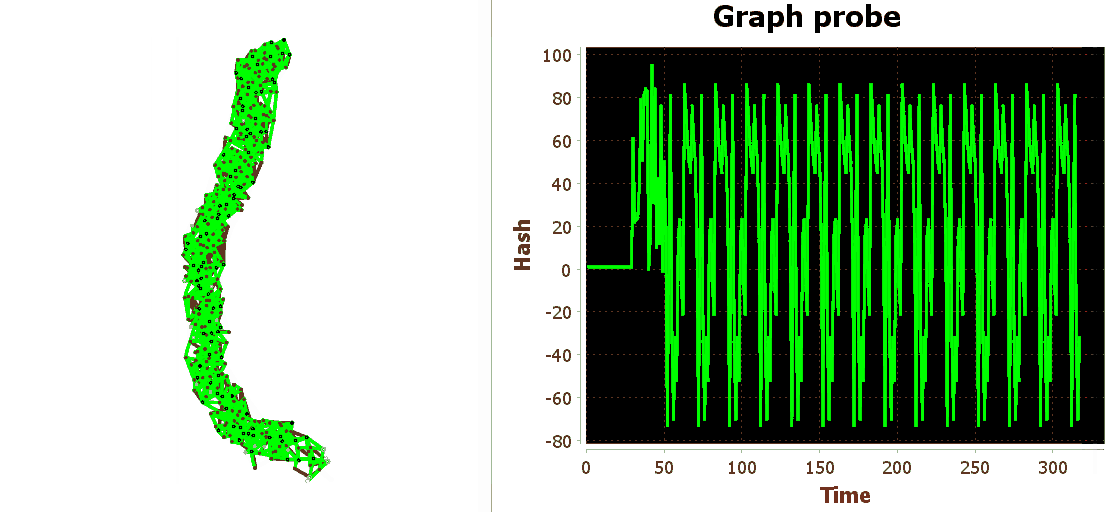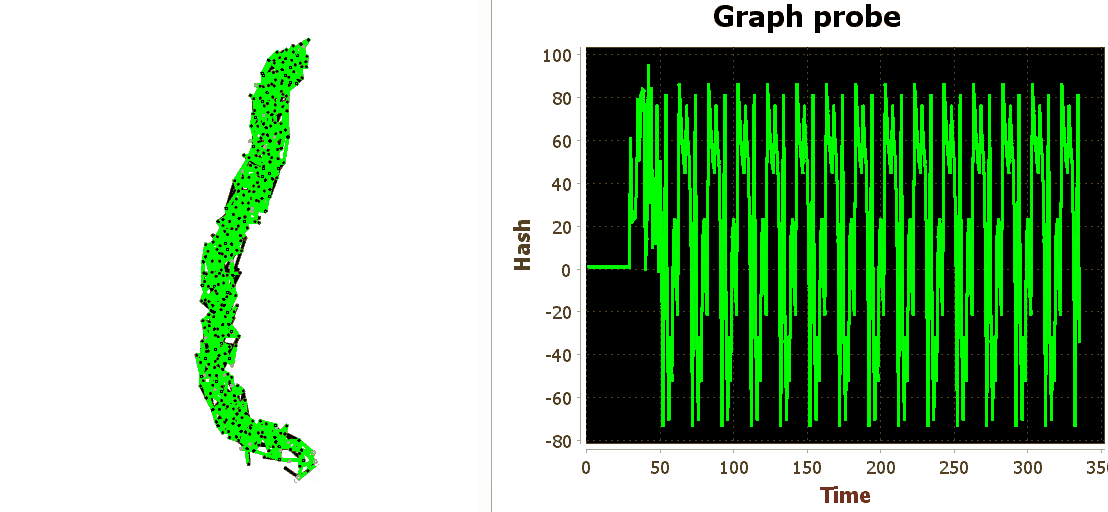
Итак, видим что, при попадании на сеть знакомого паттерна, внутри сети разыгрывается та же динамика, что и при первом знакомстве с паттерном.
Внимательный читатель может заподозрить подвох
и сказать, что начальный участок графика хэш функции, примерно с 0 по 50 такты не похож на последующие, явно повторяющиеся.
Можем заглянуть глубже и присмотреться к динамике состояний отдельных узлов. На рисунке ниже распечатаны активные узлы. Строка соответствует номеру такта. Видим — подвоха нет, просто хэш-функция вычисляется от различного количества узлов в начальный период роста сети.
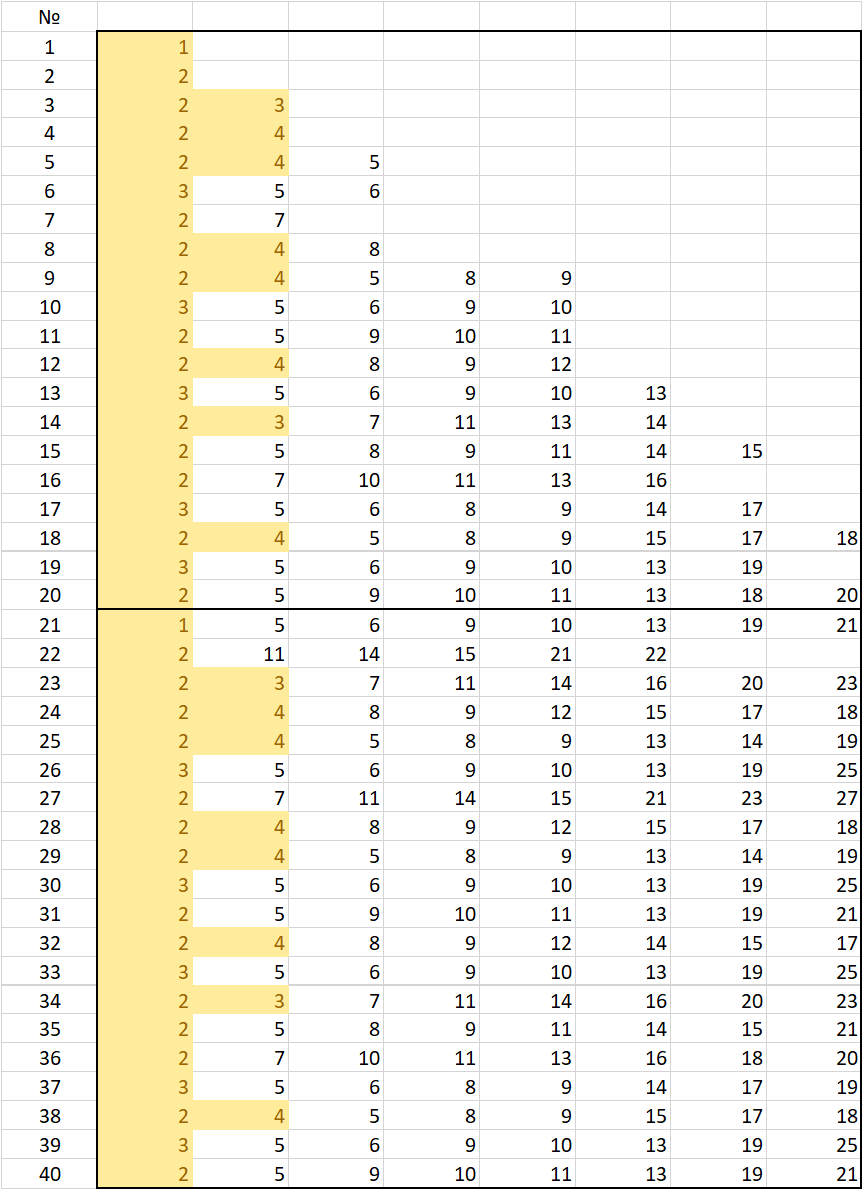
Это настолько важное наблюдение, что я его даже повторю другими словами:
Взаимодействие паттерна со структурами долговременной памяти, которые были изначально созданы паттерном, порождает точно такую же активность в сети, но уже в режиме кратковременной памяти.
Тут надо пояснить, что я имею в виду. Долговременная память — это опыт, переложенный в структуру сети. Кратковременная память — это текущее состояние активности каждого узла и связи сети, когда некий входящий паттерн взаимодействует со структурой в рассматриваемый промежуток времени. Ниоткуда вдруг появившиеся физиологические термины нам показывают параллели между сетью и объектом пристального внимания физиологии — человеком.
На самом деле, всё равно непонятно, что в этом хорошего, что сеть реагирует одинаково на знакомый паттерн. А вот что.
Мы добились не только взаимно однозначного преобразования потока данных в структуру, но также добились, что созданная структура пропускает поток, создавший её, без какого-либо сопротивления, не рассеивает его, создавая связи с каждым новым узлом. Узлы, к моменту прихода в них сигнала, не блокируют его распространение, а занимают правильное состояние, перенаправляя поток вглубь по сети. Поток данных взаимодействует со структурой, по которой он, собственно, и течёт, заставляя своим появлением (вот она — локальность взаимодействия!) срабатывать «переключатели» в узлах.
Я не настоящий дискретный математик, поэтому сейчас боюсь делать сильные заявления, но.. получается, мы поточным образом (т.е. с помощью самой последовательности) создали «распознаватель последовательностей»?
Вырожденный поток
Корректная работа в граничных случаях, согласитесь, является признаком хорошей технологии. И нам хотелось бы проверить как сеть будет разрастаться в отсутствие входящих и выходящих узлов. А так как в предыдущем разделе мы выяснили, что сеть умеет распознавать записанный в своей структуре паттерн, то, в отсутствие входов и выходов, нам бы тоже хотелось лишний раз подтвердить этот факт.
Опишу, что происходит в эксперименте. Сеть не имеет ни входящих, ни выходящих узлов. Все первые 20 тактов мы видим один активный (зелёный) узел. По прошествии 20 тактов, для наглядности, запрещается рост сети. Далее возбуждается нулевой (самый первый) узел, что с точки зрения сети означает распознавание паттерна с отметкой времени 0. В течение последующих 20 тактов мы видим последовательное продвижение потока по узлам сети, что соответствует уже увиденному ранее потоку, в данном случае вырожденному (отсутствующему).

Фрактальный поток
До текущего момента мы заставляли сеть расти под воздействием либо случайных, либо повторяющихся паттернов. А как себя поведёт сеть, если подавать на неё фрактальный поток?
Наверняка, можно придумать 100500 способов построения фрактального потока, в зависимости от смысла, который вы вкладываете в это понятие. Мне пришёл в голову следующий простой способ генерации.
Java
int[] transform(int[] pattern, int[] current) { return Arrays.stream(current) .mapToObj(value -> value == 0 ? new int[]{0} : pattern) .flatMapToInt(IntStream::of) .toArray(); }-
Берем не сильно большую последовательность нулей и единиц.
-
Вместо каждой единицы подставляем исходную последовательность. Ноль не трогаем.
-
Повторяем п.2.
Применив это правило 7 раз к массиву [1,0,1,1,1,1,1,0] получим массив с числом элементов равным 2351462.
Исходные 2000 элементов массива, на основе которого и была построена сеть
1, 0, 1, 1, 1, 1, 1, 0, 0, 1, 0, 1, 1, 1, 1, 1, 0, 1, 0, 1, 1, 1, 1, 1, 0, 1, 0, 1, 1, 1, 1, 1, 0, 1, 0, 1, 1, 1, 1, 1, 0, 1, 0, 1, 1, 1, 1, 1, 0, 0, 0, 1, 0, 1, 1, 1, 1, 1, 0, 0, 1, 0, 1, 1, 1, 1, 1, 0, 1, 0, 1, 1, 1, 1, 1, 0, 1, 0, 1, 1, 1, 1, 1, 0, 1, 0, 1, 1, 1, 1, 1, 0, 1, 0, 1, 1, 1, 1, 1, 0, 0, 1, 0, 1, 1, 1, 1, 1, 0, 0, 1, 0, 1, 1, 1, 1, 1, 0, 1, 0, 1, 1, 1, 1, 1, 0, 1, 0, 1, 1, 1, 1, 1, 0, 1, 0, 1, 1, 1, 1, 1, 0, 1, 0, 1, 1, 1, 1, 1, 0, 0, 1, 0, 1, 1, 1, 1, 1, 0, 0, 1, 0, 1, 1, 1, 1, 1, 0, 1, 0, 1, 1, 1, 1, 1, 0, 1, 0, 1, 1, 1, 1, 1, 0, 1, 0, 1, 1, 1, 1, 1, 0, 1, 0, 1, 1, 1, 1, 1, 0, 0, 1, 0, 1, 1, 1, 1, 1, 0, 0, 1, 0, 1, 1, 1, 1, 1, 0, 1, 0, 1, 1, 1, 1, 1, 0, 1, 0, 1, 1, 1, 1, 1, 0, 1, 0, 1, 1, 1, 1, 1, 0, 1, 0, 1, 1, 1, 1, 1, 0, 0, 1, 0, 1, 1, 1, 1, 1, 0, 0, 1, 0, 1, 1, 1, 1, 1, 0, 1, 0, 1, 1, 1, 1, 1, 0, 1, 0, 1, 1, 1, 1, 1, 0, 1, 0, 1, 1, 1, 1, 1, 0, 1, 0, 1, 1, 1, 1, 1, 0, 0, 0, 0, 1, 0, 1, 1, 1, 1, 1, 0, 0, 1, 0, 1, 1, 1, 1, 1, 0, 1, 0, 1, 1, 1, 1, 1, 0, 1, 0, 1, 1, 1, 1, 1, 0, 1, 0, 1, 1, 1, 1, 1, 0, 1, 0, 1, 1, 1, 1, 1, 0, 0, 0, 1, 0, 1, 1, 1, 1, 1, 0, 0, 1, 0, 1, 1, 1, 1, 1, 0, 1, 0, 1, 1, 1, 1, 1, 0, 1, 0, 1, 1, 1, 1, 1, 0, 1, 0, 1, 1, 1, 1, 1, 0, 1, 0, 1, 1, 1, 1, 1, 0, 0, 1, 0, 1, 1, 1, 1, 1, 0, 0, 1, 0, 1, 1, 1, 1, 1, 0, 1, 0, 1, 1, 1, 1, 1, 0, 1, 0, 1, 1, 1, 1, 1, 0, 1, 0, 1, 1, 1, 1, 1, 0, 1, 0, 1, 1, 1, 1, 1, 0, 0, 1, 0, 1, 1, 1, 1, 1, 0, 0, 1, 0, 1, 1, 1, 1, 1, 0, 1, 0, 1, 1, 1, 1, 1, 0, 1, 0, 1, 1, 1, 1, 1, 0, 1, 0, 1, 1, 1, 1, 1, 0, 1, 0, 1, 1, 1, 1, 1, 0, 0, 1, 0, 1, 1, 1, 1, 1, 0, 0, 1, 0, 1, 1, 1, 1, 1, 0, 1, 0, 1, 1, 1, 1, 1, 0, 1, 0, 1, 1, 1, 1, 1, 0, 1, 0, 1, 1, 1, 1, 1, 0, 1, 0, 1, 1, 1, 1, 1, 0, 0, 1, 0, 1, 1, 1, 1, 1, 0, 0, 1, 0, 1, 1, 1, 1, 1, 0, 1, 0, 1, 1, 1, 1, 1, 0, 1, 0, 1, 1, 1, 1, 1, 0, 1, 0, 1, 1, 1, 1, 1, 0, 1, 0, 1, 1, 1, 1, 1, 0, 0, 0, 1, 0, 1, 1, 1, 1, 1, 0, 0, 1, 0, 1, 1, 1, 1, 1, 0, 1, 0, 1, 1, 1, 1, 1, 0, 1, 0, 1, 1, 1, 1, 1, 0, 1, 0, 1, 1, 1, 1, 1, 0, 1, 0, 1, 1, 1, 1, 1, 0, 0, 0, 1, 0, 1, 1, 1, 1, 1, 0, 0, 1, 0
Строим сеть, подавая данные на единственный (для простоты) входящий узел.

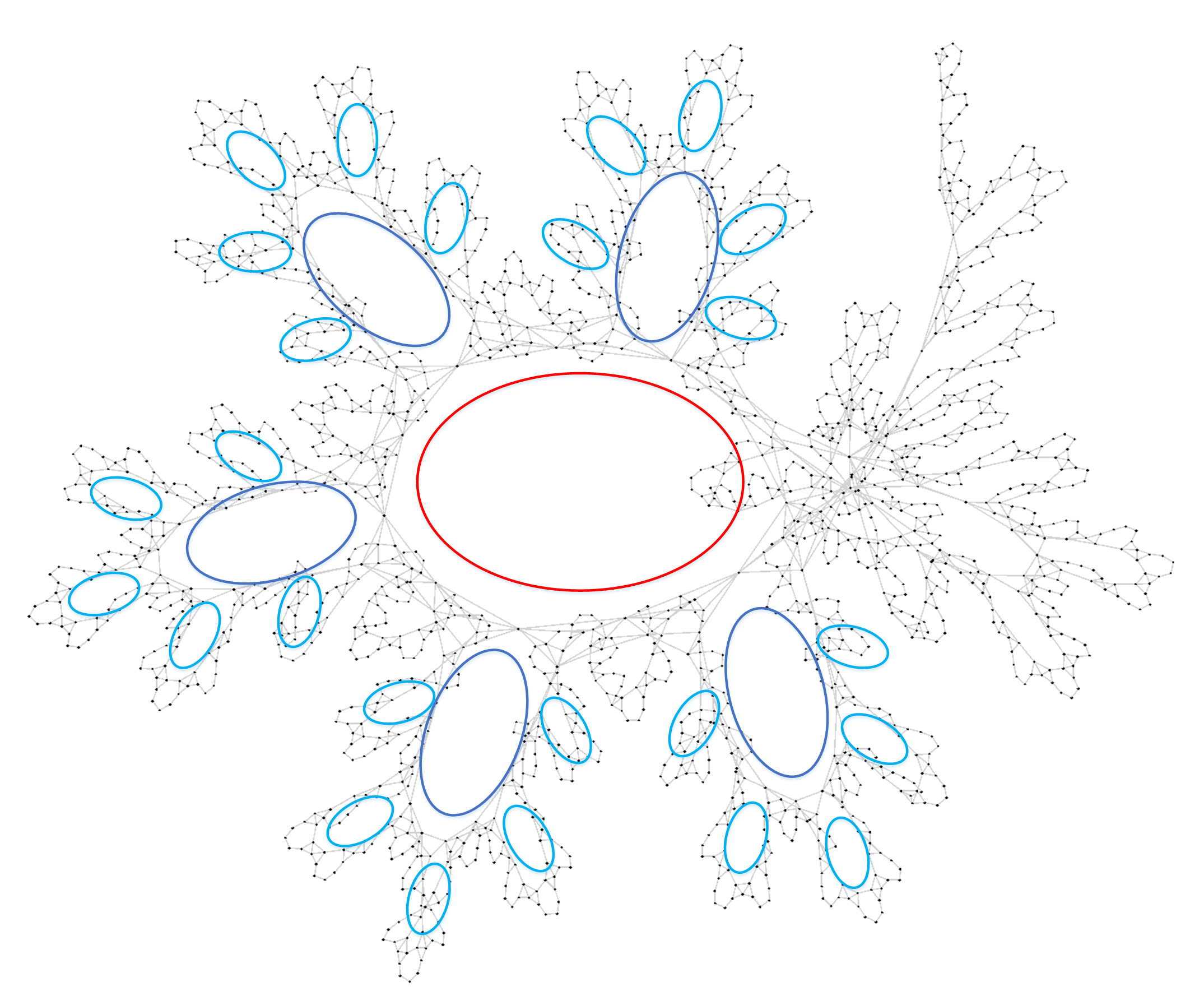
На самом деле то, что используемая мной библиотека для визуализации графов, уложила сеть в явную фрактальную картину — это скорее исключение, чем правило. Чаще всего, получалось что-то вроде этого, разумеется, на разных сетях:

Правила связывания нового узла
Все показанные выше анимированные картинки с разрастанием сети относились к режиму, когда сеть не имеет выходящих узлов. В этом режиме правила связывания нового узла описываются и, что более важно, реализуются в коде существенно более просто, чем в случае, когда у сети есть выходящие узлы.
Попробуем подобраться к правилам связывания нового узла, когда сети требуется подстройка под сигналы обратной связи от среды. Выше мы за счёт фрактальности чёрного ящика обосновали абсолютную естественность наличия механизма подстройки структуры ящика с помощью нового узла в структуре сети.
Каждый новый узел в структуре сети — это возможность передать или заблокировать поток в целевых узлах. Состояние внутренних и выходных узлов сети просто подстраивается посредством введения нового узла.
Т.к. новый узел, создавая связи с логически более старыми узлами, сеть из сети прямого распространения превращается в рекуррентную, что на порядок усложняет разработку.
Состояние разработки
Первоначальный вариант кода устарел, репозиторий в статусе abandoned, если хотите — используйте, но на свой страх и риск. В настоящее время разработка ведётся в новом приватном репозитории.
Сеть корректно растёт только в режиме приёма потока с входящих узлов. Мне не удалось на момент написания статьи запрограммировать связывание нового узла в режиме «обучения с учителем», когда сеть подстраивается под ответы среды.
Однако, «движок сети» (рекурсивный алгоритм обхода узлов графа) корректно отрабатывает любые собранные вручную (искусственно, т.е. не нативным образом) структуры сети.
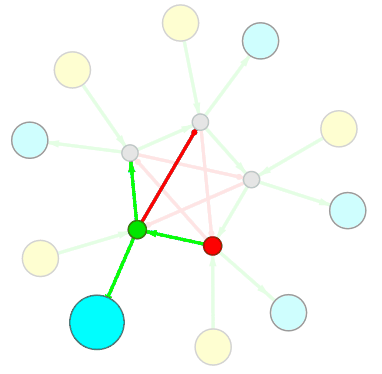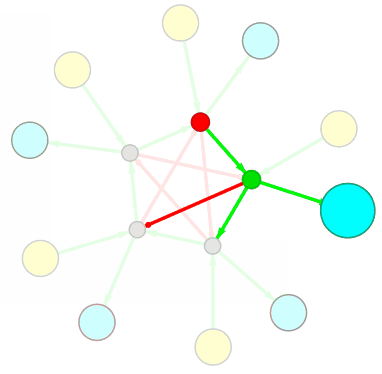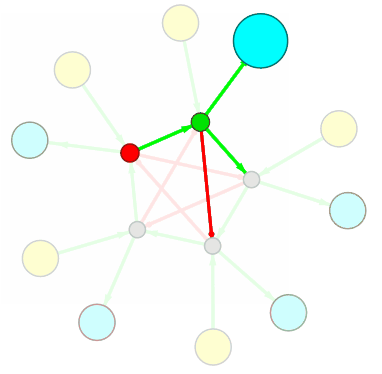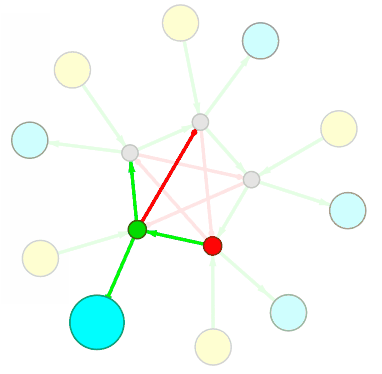
Правила связывания нового узла разработаны (искренне хотелось бы в это верить). На бумаге мне удаётся собирать простенькие преобразователи и проверять их работоспособность с помощью корректно работающего механизма рекурсивного обхода графа. Например, такой преобразователь (1010 → 1100) был собран вручную, основываясь на правилах связывания нового узла:
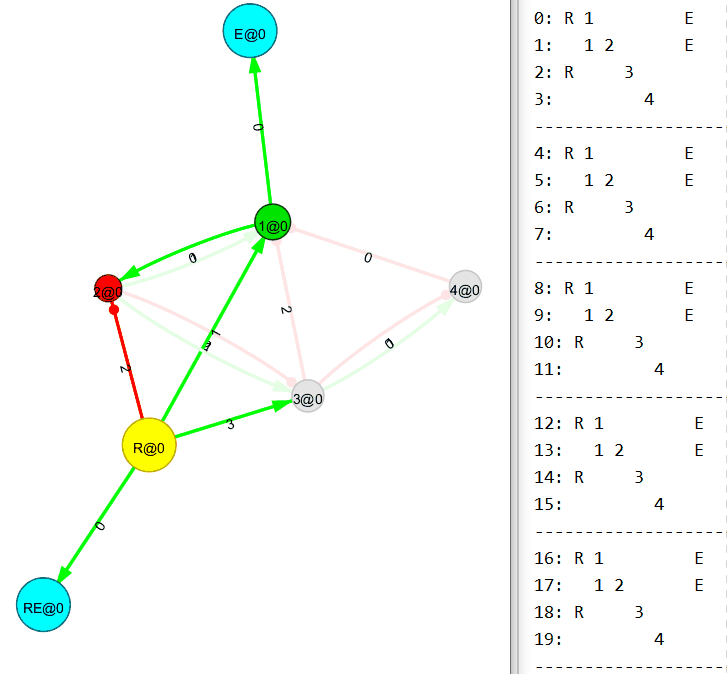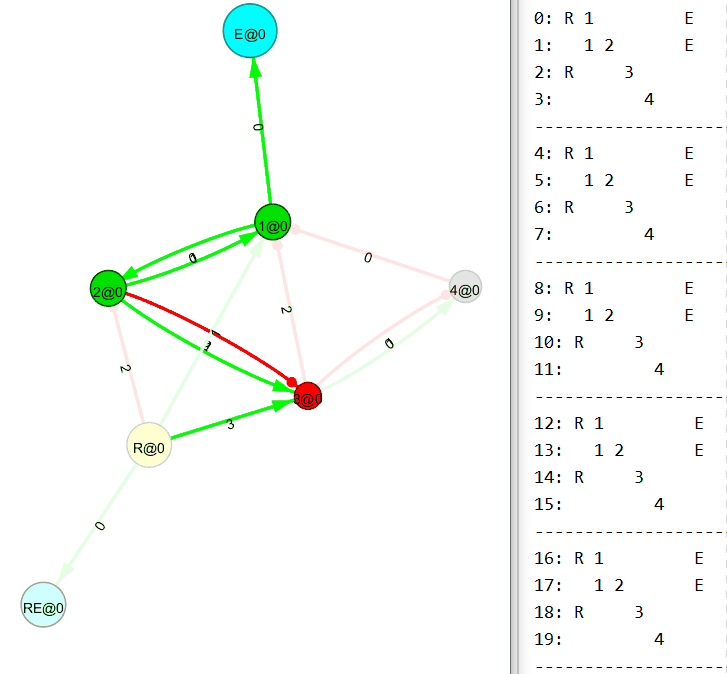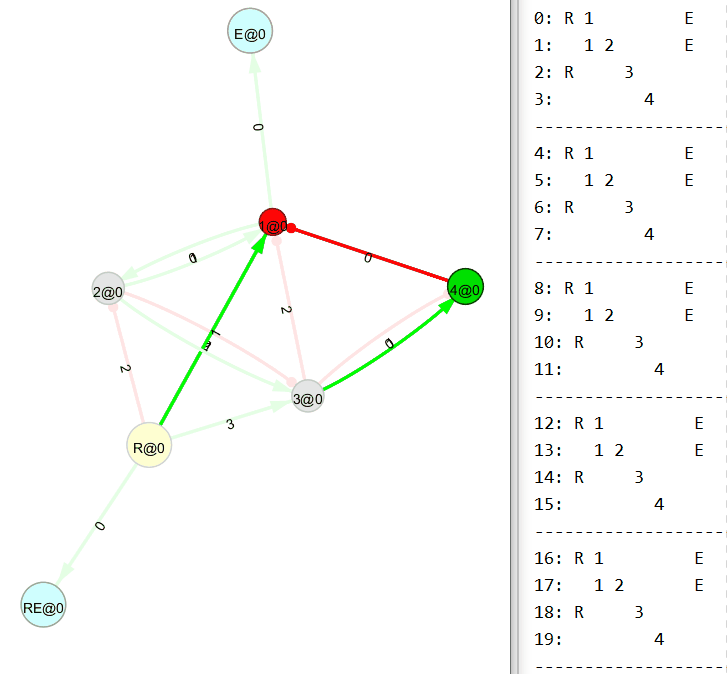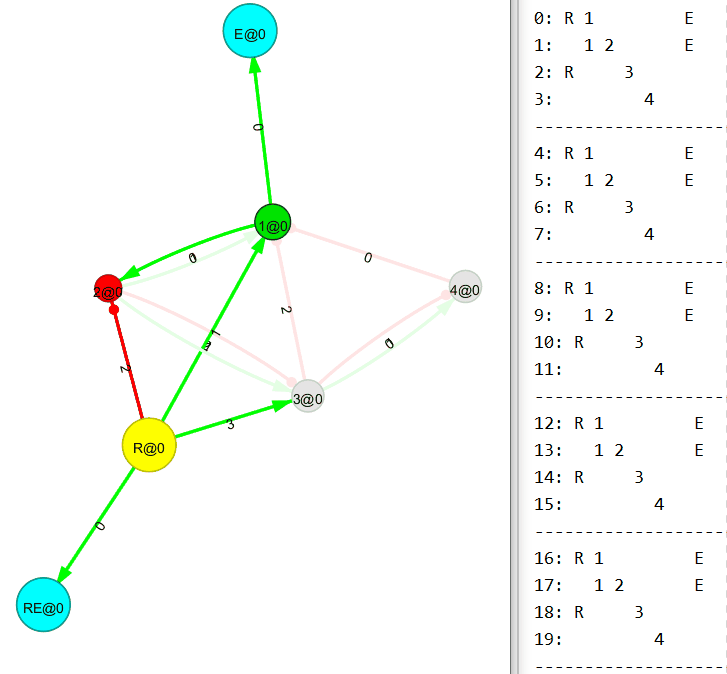
Сферические кони в вакууме
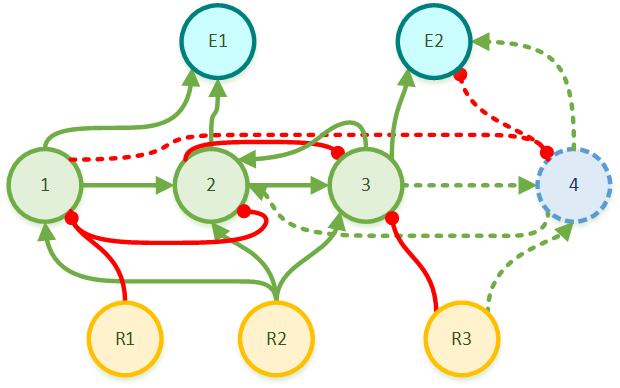
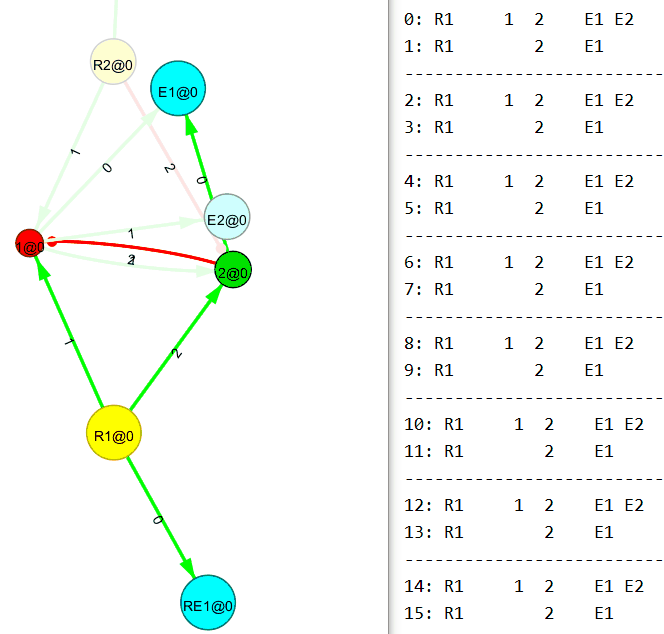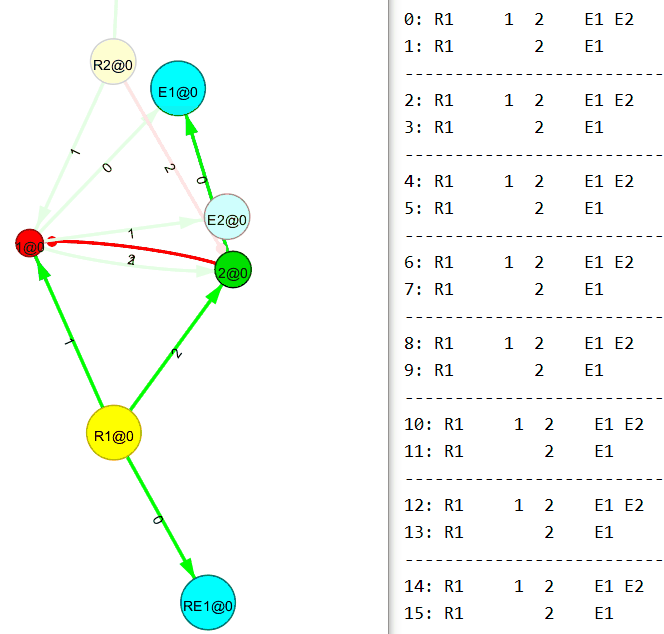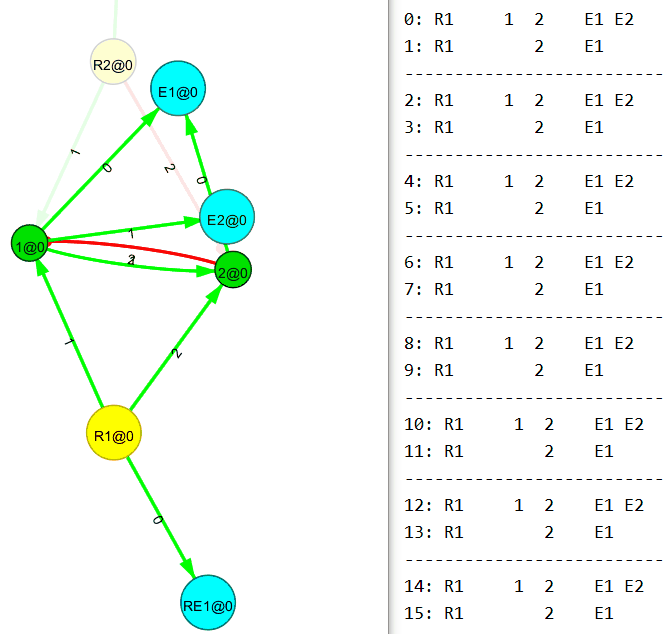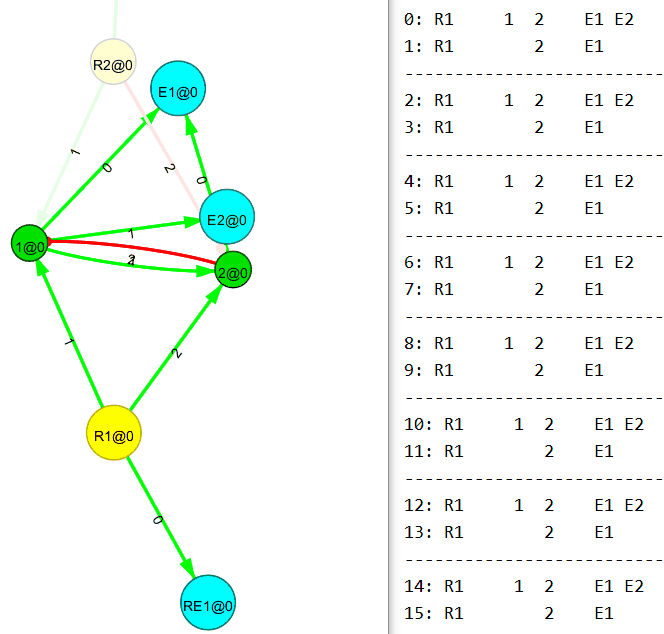
Ниже 2×2 многополюсник, также собранный вручную с применением правил связывания нового узла.
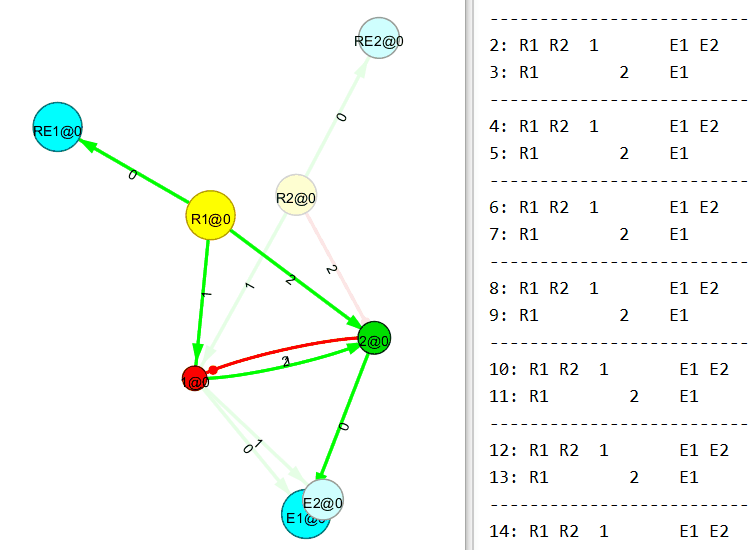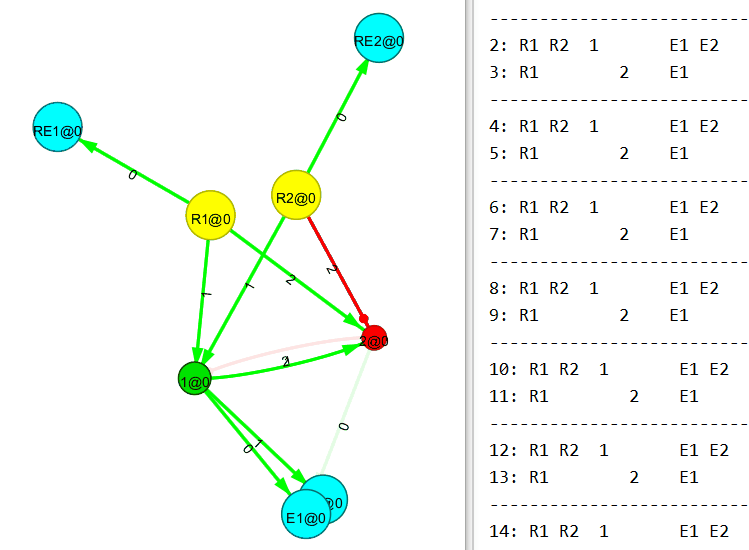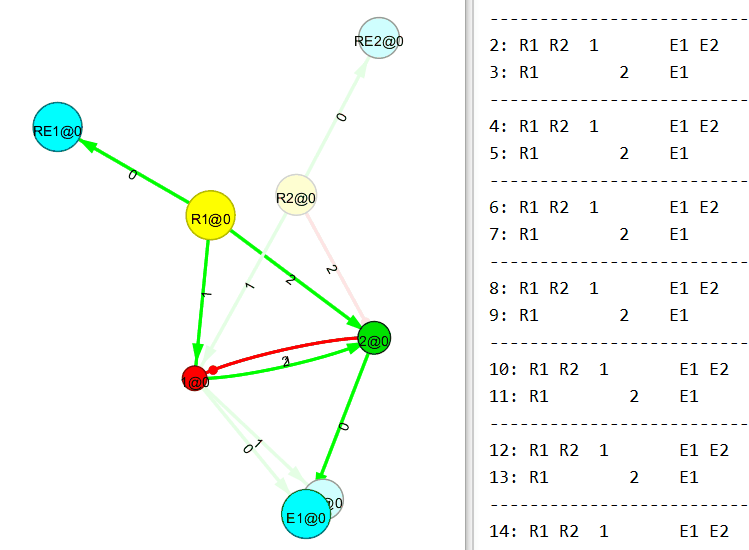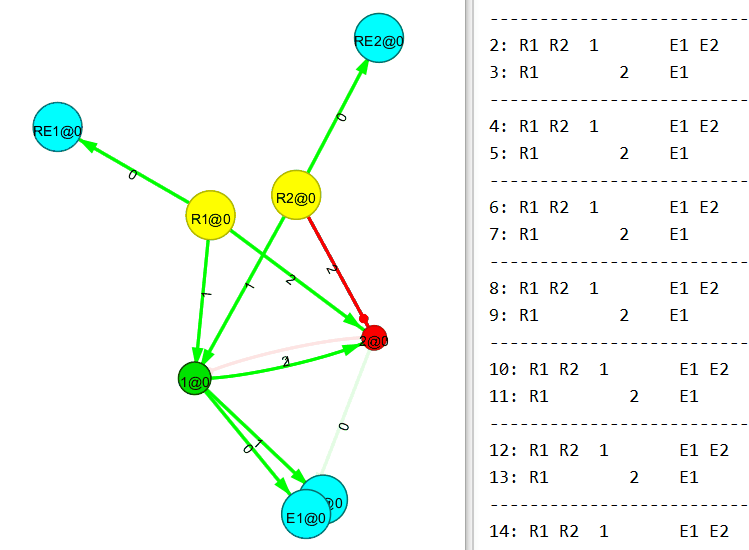
А вот сейчас будет интересное. Понимаю, пример тривиальный, но всё же.
Убираем входящий поток на первый (R1) узел. И…
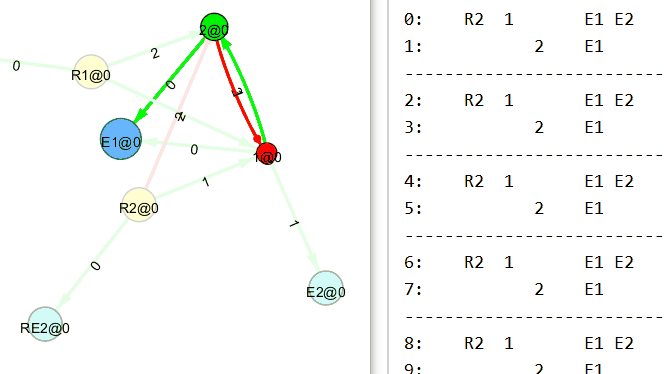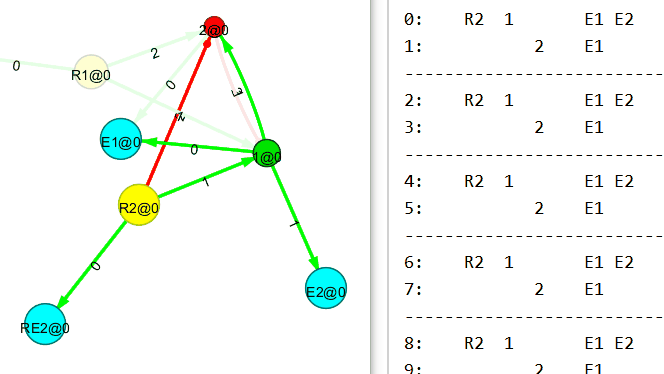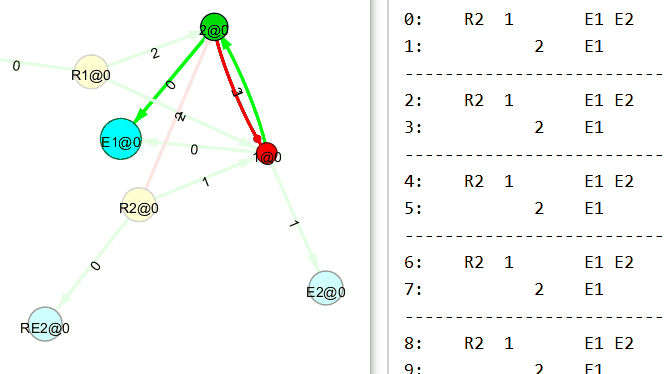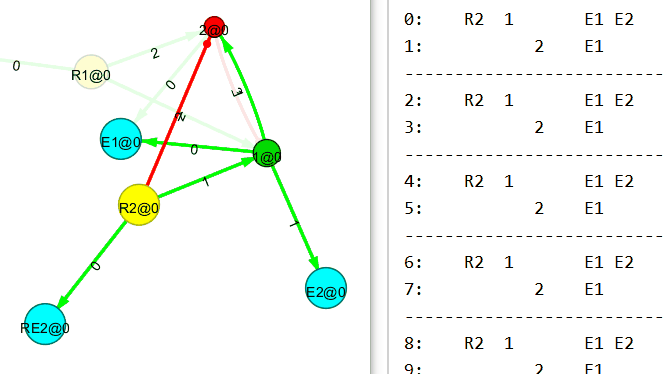
Теперь убираем входящий поток на второй (R2) узел. И…
Игра жизнь и саморепликация сети
Вернёмся ненадолго к тому, с чего начали — с задачи моделирования жизни на компьютере.
Не берусь ничего утверждать, а лишь хочу провести параллели, «на подумать». Организмы в живой природе развиваются из генетического кода, записанного в молекулярной структуре. Наверное, они еще как-то умеют развиваться, но я не настоящий биолог и беру один понравившийся мне вариант полового размножения.
Генетический код, записанный в молекулярной структуре, и помещенный в защищенную среду, т.е. фильтрующую нежелательные события, естественным образом развивается во взрослую особь, способную к передаче уже своего генетического кода с приобретёнными в ходе развития полезными дополнениями.
Люди (Человек) появляются в ходе протекания процессов в реальности. В ходе протекания процессов на компьютере (надеюсь, все понимают) люди появится не могут. Поэтому пытаться как-то применять понятийный аппарат, свойственный человеку в целом и его высшей нервной деятельности в частности, в отношении предлагаемых в статье алгоритмов, по-хорошему, не стоит.
Способность сети формировать одинаковую структуру при одинаковых потоках внешних данных является её базовой особенностью. Поэтому, мне было бы интересно разобраться в способности сети самореплицироваться, спроектировать и запрограммировать подобие игры Жизнь с объектами, способными к усложнению поведения в условиях бифуркаций.
Какие плюсы у сети, одним списком
Вы встретите несколько раз слово Естественный ниже в перечислениях хороших качеств сети. Оно означает, что свойство, рядом с которым употреблено прилагательное Естественный, присутствует неразрывно с другими полезными свойствами, его невозможно оторвать от других качеств сети, его не придумали специально и не внедрили силой для соответствия модным тенденциям.
Перечисленные положительные свойства, возможно, не в полной мере обоснованы выше в теле статьи, но всё ж они тут будут:
-
Continual (lifelong, incremental) learning, т.е. естественная способность накапливать опыт в течение всего срока жизни сети.
-
One-shot learning, т.е. естественная способность усвоить информацию с первого раза
-
Отсутствие катастрофического забывания. Сеть запоминает вообще весь входящий поток. При этом не работает как стек.
-
Простое и эффективное сосуществование долговременной и кратковременной памяти
-
Распознавание пространственно-временных паттернов в режиме потери части данных
-
Распознавание пространственно-временных паттернов в режиме с шумами
-
Принципиальное отсутствие числовых параметров
-
Естественная работа с категориальными (нечисловыми) типами данных
-
(Потенциально) частное решение задачи чёрного ящика за один проход по данным
Что я жду
Появления в комментариях дискретных математиков, криптографов, автоматчиков и ТАУ теоретиков с обоснованиями зря потраченного времени, либо конструктивной критикой, дельными вопросами и предложениями экспериментов.
Очень интересует прикладное направление. Если знаете отрасль с проблемами, которые закрываются полезными свойствами сети — пишите.
Обсуждение человеческого интеллекта и мышления интересует в последнюю очередь.
ссылка на оригинал статьи https://habr.com/ru/post/696384/
Добавить комментарий