2 2 2 2 = 7

В общем случае задача выглядит как поиск знаков арифметических операций и иных действий без использования других цифр для того, чтобы получить из четырёх двоек любое число от 0 до 9.

Довольно простые решения на сложение, деление и возведение в степень есть для всех чисел, кроме 7.

С 7 же нужно выйти за рамки привычного (помните головоломку про соединение точек и выход из зоны квадрата). По решению задачи можно многое узнать о собеседнике.

На этом моменте предлагаю остановиться тем, кто хочет испытать свои силы.

Первое решение — это читерское округление. Корень из 222, делённый на 2, это иррациональное число 7.44983..

Решение грубое, но действенное.

Следующий путь — использование логарифма. В какую степень надо возвести 2, чтобы получить корень из 2. А если взять из результата логарифм по основанию 2?

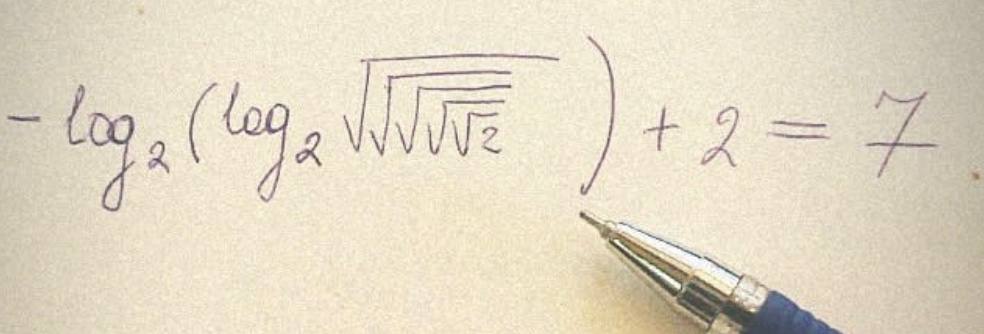
Это решение для сильных духом, которые всегда найдут ответ. Ведь у любой операции (возведение в степень) есть обратная.

Третий вариант — двойной факториал. Двойной факториал (перемножение с шагом 2) от 4 это 4*2=8.

2*2!! — 2/2 = 7

Факториал не изучают в школе, но он точно нужен в комбинаторике и мат анализе, поэтому такое решение подвластно тем, кто не забыл свои первые курсы в универе, хотя тогда казалось, что высшая математика в жизни не пригодится.

Четвёртое решение — элегантная перестановка слагаемых.

2/2 = 7 в степени (2-2)

Тоже читерство, но уже другого рода. Если что-то мешается, то можно это вынести за знак равенства и сделать с этим что-то уже там. Я бы сказала, предпринимательский подход. Решение предложил один из бывших руководителей Газпрома.

Пятое решение — это тригонометрия. Подход визуализаторов.

cos(2pi) + 2 + 2 + 2 = 7

sin(pi/2) + 2 + 2 + 2 = 7

Легендарное Пи — это, конечно, не цифра. Но ее использование открывает дверь к решениям с константой.

6) 2 + 2 + 2 + 2 — x/x = 7

И, наконец, седьмое решение. Мое любимое. Очень прогерское.

222/2 = 111

А 111 в двоичной системе исчисления — это искомое семь.

Пока это все решения, которые удалось найти. Если у вас есть что-то ещё, пишите в комментариях.