Реализация алгоритма Дейкстры для поиска оптимального пути между двумя точками на поверхности и обхода препятствий

Приветствую Вас, Хабровчане!

Я думаю, по названию статьи и так понятно о чем я Вам буду рассказывать в этой работе. Поэтому не вижу смысла в длинных преамбулах и аннотациях. Ну а для тех, кто совсем не в теме и фамилию известного нидерландского ученого видят впервые — отправляю Вас на википедию с его биографией и алгоритмом, о котором далее пойдет речь.

И да, я прекрасно понимаю, что я далеко не первый и не последний кто находит в себе силы попробовать на практике реализовать этот алгоритм. Как говорится, повторение — мать учения. Поэтому не нужно меня за это закидывать камнями, палками и чем бы то ни было. Я лишь предложу свой вариант реализации и продемонстрирую результаты. Как Вы уже догадались, писать будем на языке C#. Исходники найдете здесь.

Поехали!

Содержание

• Математическая постановка задачи

• Графы и алгоритм Дейкстры

• Превращаем поверхность в граф

• Численная реализация

• Результаты расчетов. Простые препятствия

• Лабиринты

• Поиск оптимального пути на поверхности

• Заключение

Математическая постановка задачи

В декартовой прямоугольной системе координат на плоскости задана равномерная сетка:

где — узлы сетки; — шаги сетки;— количество точек по осии, соответственно. В каждом узле сетки задано значение , представляющее собой высоту карты (ландшафта) местности в рассматриваемой точке. Значения , образующие исследуемую поверхность, могут быть отрицательными — в таком случае высоту карты следует понимать как глубину относительно некоторой нулевой отметки .

Заданы стартовая и целевая точка искомого оптимального маршрутаи, рисунок 1.

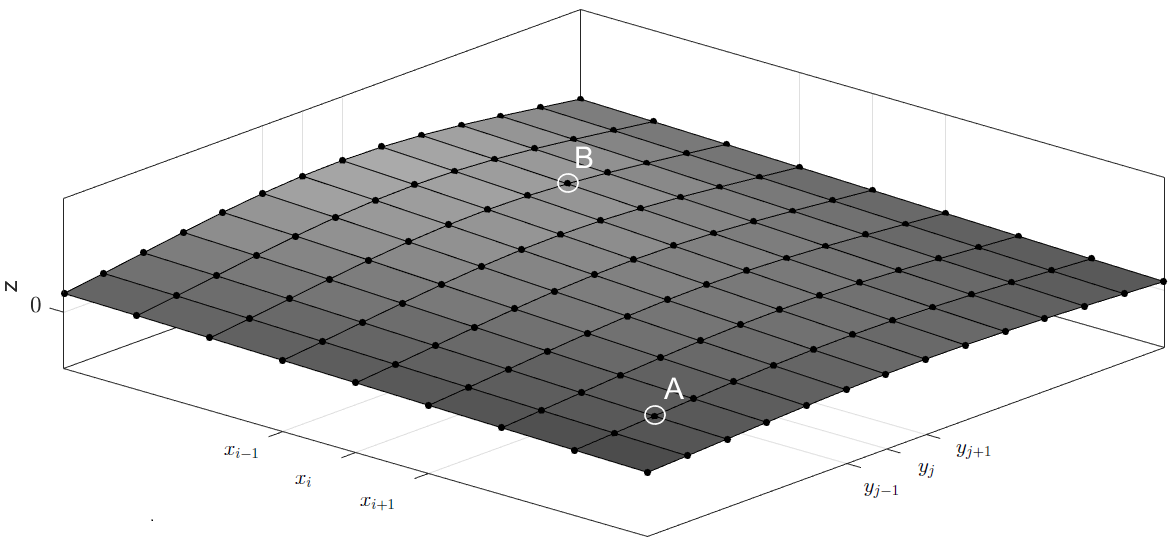
На выходе мы должны получить конечный список (массив) координат, следуя по которым мы доберемся из точкив точкунаиболее оптимальным образом.

Также в алгоритме будет учитываться параметр, задающий максимальный угол уклона (в градусах) для поиска подходящих соседей.

Так, ну а при чем тут графы и какой-то алгоритм ?!

Графы и алгоритм Дейкстры

Алгоритм Дейкстры представляет собой глобальный алгоритм поиска кратчайших путей на взвешенном графе. О том, что такое граф, и с чем его едят, что такое вершина, ребро, какие графы бывают — я здесь Вам рассказывать не буду. На тему графов написано немало хороших книг, на одну из которых я дам ссылку в конце статьи. А пока я буду предполагать, что Вы уже знакомы с основными понятиями теории графов. Хотя, как по мне, большинство терминов, которые будут описаны далее в статье должны быть понятны и ежу на интуитивном уровне.

Как я упомянул выше, алгоритм Дейкстры является глобальным, я бы даже сказал самым глобальным из всех подобных. Имеются и другие алгоритмы, которые в ряде случаев оптимизируют и ускоряют поиск, например, такие как алгоритм Ли, алгоритм A* и др. Очень хороший обзор на алгоритмы поиска (в т.ч. и Дейкстры) да еще и с примерами кода можете найти тут.

Ну а я просто захотел попробовать сделать это своими силами. Как говорится, хочешь сделать что-то хорошо — сделай это сам! =)

Так в чем же именно глобальность алгоритма Дейкстры?! Глобальность в том, что даже если нам будет необходимо найти кратчайший путь между двумя смежными вершинами графа, в котором 1000 вершин, нам так или иначе придется перебрать абсолютно все 1000 вершин.

Поясню это на примере взвешенного графа с 6-ю вершинами, рисунок 2.

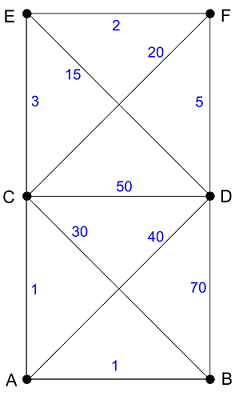
Найдем кратчайший путь из вершиныдо вершины. Даже не «запуская» на этом графе алгоритм Дейкстры, очевидно, что кратчайший путь изв будет путь , длина которого равна . Так вот, несмотря на то, что вершиныисмежные — нам все равно пришлось рассматривать ВСЕ вершины этого графа. В этом и заключается глобальность, и в то же время сложность этого алгоритма (я специально подобрал весовые коэффициенты для некоторых ребер намного большими чем другие).

Превращаем поверхность в граф

Чтобы решить нашу задачу с помощью алгоритма Дейкстры нам нужно каким-то образом «превратить» нашу исследуемую поверхность во взвешенный граф. Делать будем это так, — посмотрим на нашу поверхность сверху (перпендикулярно плоскости ), вид будет примерно такой, рисунок 3:

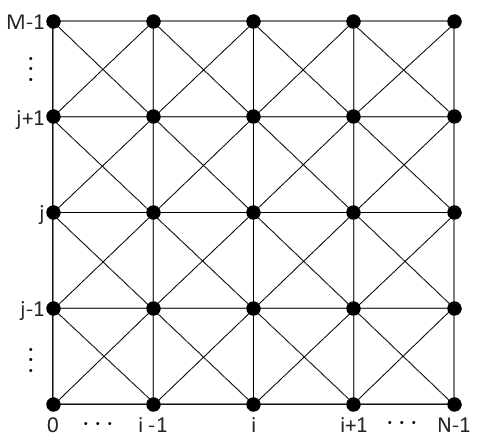
Точки поверхности будут спроецированы на плоскость— это и будут вершины нашего графа. Но откуда появились эти «крестики» в каждом квадратике, спросите Вы ?! Эти крестики — тоже ребра графа, которые добавлены для того, чтобы у нас была возможность ходить не только по горизонтали и вертикали, но и по диагонали. Да, это сильно увеличит сложность алгоритма и время расчета, но зато путь будет еще более оптимальным.

Таким образом любую вершину подобного графа можно идентифицировать с помощью координаты , что нам очень пригодится в дальнейшем для хранения всех вершин графа в виде матрицы.

Наш граф должен быть взвешенным. Вот тут, конечно, можно поиграться и задавать весовые коэффициенты любым изощренным способом. Но я пока поступлю просто — весребра, соединяющего смежные вершины и , заданные своими координатамибудет не что иное как расстояние в пространстве между соответствующими точками поверхности, из которой наш граф был построен:

Рассматриваемый граф является связным (причем степень связности достаточно неплохая!, особенно после добавления диагональных ребер), поэтому «тупиковых» ситуаций возникнуть не должно и если все учтено правильно, алгоритм все-таки после долгих блужданий доберется из стартовой в целевую вершину и на своем пути «переберет» абсолютно все вершины графа.

Ну все…осталось запустить алгоритм Дейкстры!

Само собой при численной реализации этого алгоритма возникнут определенные сложности много костылей и вопросы. Их я уже буду комментировать в процессе объяснения написанного кода.

Численная реализация

Кодить, как я уже говорил будем на C#, поэтому постараемся взять все самое лучшее из возможностей этого языка. А возможностей у него немало.

Я создам в Visual Studio консольный проект (.NET 4.7.2). Ключевыми классами будут Point2D.cs, Vertex.cs и Graph.cs. Начнем с самого простого.

Класс Point2D будет содержать всего два свойства для хранения координат вершины графа:

public class Point2D     {         public int i { get; }         public int j { get; }          public Point2D(int i, int j)         {             this.i = i;             this.j = j;         }     }

С классом Vertex уже чуть поинтереснее:

public class Vertex     {         public Point2D Coordinate { get; set; }         public double Height { get; set; }         public Point2D CameFrom { get; set; }         public double Label { get; set; }         public bool IsVisited { get; set; }         public bool IsGoal { get; set; }         public bool IsObstacle { get; set; }          public Vertex(int i, int j, Point2D CameFrom = null, double Height = 0.0, double Label = double.MaxValue, bool IsVisited = false, bool IsGoal = false, bool IsObstacle = false)         {             Coordinate = new Point2D(i, j);             this.CameFrom = CameFrom;             this.Height = Height;                        this.Label = Label;             this.IsVisited = IsVisited;             this.IsGoal = IsGoal;             this.IsObstacle = IsObstacle;         }     }

Опишу кратко свойства.

Первое из них — это координаты вершины графа; Height — высота, значение функции в точке вершины, необходимое для расчета весового коэффициента и величины уклона между двумя смежными вершинами; CameFrom — здесь в процессе работы алгоритма будут храниться координаты вершины из которой мы попали в текущую вершину — на основании этого свойства мы в конце работы алгоритма сформируем наш искомый маршрут; Label — метка, хранящая значение длины пути из стартовой вершины в текущую; IsVisited — говорит нам посетили ли мы данную вершину в процессе расчета или нет; IsGoal — данное свойство будет истинным только для целевой вершины графа (та вершина, оптимальный путь к которой мы ищем). Это свойство понадобилось мне для того, чтобы алгоритм Дейкстры не завершился раньше времени и мы обошли абсолютно все вершины графа; IsObstacle — наш алгоритм будет также уметь обходить препятствия, например, искать кратчайший путь в лабиринте, это свойство позволяет задать определенные вершины как вершины-препятствия, чтобы выбрасывать их из рассмотрения наряду с уже посещенными.

Теперь о классе Graph.

 public class Graph     {         /// <summary>         /// Шаг сетки по оси Ox         /// </summary>         public double dx { get; }         /// <summary>         /// Шаг сетки по оси Oy         /// </summary>         public double dy { get; }         /// <summary>         /// Количество вершин по оси Ox         /// </summary>         public int N { get; }         /// <summary>         /// Количество вершин по оси Oy         /// </summary>         public int M { get; }         /// <summary>         /// Матрица вершин графа         /// </summary>         public Vertex[,] Vertices { get; }         /// <summary>         /// Предельная величина уклона, необходимая для обхода препятствий, в градусах         /// </summary>         public double MaxSlope { get; } }

Для работы алгоритма реализуем несколько вспомогательных методов.

Для расчета весов и уклона нам нужно будет получать «реальные» координаты вершины графа на плоскости (с учетом величины шагов и ):

(double, double) GetRealXY(Vertex vertex)         {             double x = vertex.Coordinate.i * dx;             double y = vertex.Coordinate.j * dy;              return (x, y);         } 

Вес ребра между смежными вершинами (расстояние между точками поверхности) находим так:

double Weight(Vertex v1, Vertex v2)         {             (double, double) x1y1 = GetRealXY(v1);             (double, double) x2y2 = GetRealXY(v2);              double xDiff = x1y1.Item1 - x2y2.Item1;             double yDiff = x1y1.Item2 - x2y2.Item2;             double zDiff = v1.Height - v2.Height;              double sumOfSquares = Math.Pow(xDiff, 2.0) + Math.Pow(yDiff, 2.0) + Math.Pow(zDiff, 2.0);              return Math.Sqrt(sumOfSquares);         }

Следующий метод возвращает величину уклона между смежными вершинами (в градусах):

private double Slope(Vertex v1, Vertex v2)         {             double hypotenuse = Weight(v1, v2); // Вес ребра - это и есть по факту расстояние между точками             double zDiffAbs = Math.Abs(v1.Height - v2.Height); // Модуль разности по высоте              return Math.Asin(zDiffAbs / hypotenuse) * 180.0 / Math.PI; // Переводим радианы в градусы         }  

Для удобства реализуем 8 методов для получения соседней вершины в зависимости от направления (я привел один из них):

private Vertex GetTopVertex(Vertex v) => Vertices[v.Coordinate.i, v.Coordinate.j + 1];

И еще 8 методов для определения принадлежности вершины той или иной части сетки (здесь я привел два из них):

private bool IsTopRightVertex(Vertex v1) => v1.Coordinate.i == N - 1 && v1.Coordinate.j == M - 1;  private bool IsVertexOnTheRightSide(Vertex v1) => v1.Coordinate.i == N - 1;

Эти методы понадобятся для получения всех смежных вершин для рассматриваемой вершины. Вот тут нам придется нарубить if-ов, т.к. количество смежных вершин не всегда одно и то же:

private List<Vertex> GetAllAdjacentVertices(Vertex vertex)         {             #region Рассматриваем угловые вершины              if (IsTopRightVertex(vertex))                 return new List<Vertex>                 {                     GetLeftVertex(vertex),                     GetBottomLeftVertex(vertex),                     GetBottomVertex(vertex)                 };              if (IsBottomRightVertex(vertex))                 return new List<Vertex>                 {                     GetTopVertex(vertex),                     GetTopLeftVertex(vertex),                     GetLeftVertex(vertex)                 };              if (IsBottomLeftVertex(vertex))                 return new List<Vertex>                 {                     GetTopVertex(vertex),                     GetTopRightVertex(vertex),                     GetRightVertex(vertex)                 };              if (IsTopLeftVertex(vertex))                 return new List<Vertex>                 {                     GetBottomVertex(vertex),                     GetBottomRightVertex(vertex),                     GetRightVertex(vertex)                 };              #endregion              #region Рассматриваем боковые вершины              if (IsVertexOnTheTopSide(vertex))                 return new List<Vertex>                 {                     GetLeftVertex(vertex),                     GetBottomLeftVertex(vertex),                     GetBottomVertex(vertex),                     GetBottomRightVertex(vertex),                     GetRightVertex(vertex)                 };              if (IsVertexOnTheRightSide(vertex))                 return new List<Vertex>                 {                     GetTopVertex(vertex),                     GetTopLeftVertex(vertex),                     GetLeftVertex(vertex),                     GetBottomLeftVertex(vertex),                     GetBottomVertex(vertex)                 };              if (IsVertexOnTheBottomSide(vertex))                 return new List<Vertex>                 {                     GetLeftVertex(vertex),                     GetTopLeftVertex(vertex),                     GetTopVertex(vertex),                     GetTopRightVertex(vertex),                     GetRightVertex(vertex)                 };              if (IsVertexOnTheLeftSide(vertex))                 return new List<Vertex>                 {                     GetTopVertex(vertex),                     GetTopRightVertex(vertex),                     GetRightVertex(vertex),                     GetBottomRightVertex(vertex),                     GetBottomVertex(vertex)                 };              #endregion              // Иначе вершина лежит "в середине карты" и нужно вернуть все 8 смежных вершин             return new List<Vertex>                 {                     GetTopVertex(vertex),                     GetRightVertex(vertex),                     GetBottomVertex(vertex),                     GetLeftVertex(vertex),                      GetTopRightVertex(vertex),                     GetBottomRightVertex(vertex),                     GetBottomLeftVertex(vertex),                     GetTopLeftVertex(vertex)                 };         }

Напишем метод, который будет «отсеивать неподходящих» соседей:

private List<Vertex> GetValidNeighbors(Vertex current)         {             // Из всех смежных вершин оставляем только те, которые              // 1. Еще не посещены             // 2. Не являются вершинами-препятствиями             // 3. Наклон к которым меньше заданной величины (например, 30 градусов)             return GetAllAdjacentVertices(current).Where(v => !v.IsVisited && !v.IsObstacle && Slope(v, current) < MaxSlope).ToList();         }

и метод, который из оставшихся соседей будет отсеивать целевую вершину и сообщать осталось ли что-то после отсеивания:

private bool HasValidAndNotGoalNeighbors(Vertex vertex, out List<Vertex> validAndNotGoalNeighbors)         {             validAndNotGoalNeighbors = GetValidNeighbors(vertex).Where(v => !v.IsGoal).ToList();             return validAndNotGoalNeighbors.Any();         }

Именно этот метод (в основном) и нужен для того, чтобы мы перебрали абсолютно все вершины графа (помните о глобальности, да??!). Так как бывают кейсы, когда мы натыкаемся на целевую вершину «раньше срока» (раньше того, как алгоритм пробежит по всем вершинам графа и найдет нам оптимальный маршрут).

Также в основном while-цикле метода по поиску пути (скоро мы уже дойдем до него =)) я буду накапливать в список посещенные вершины. Это тоже относится к замечанию выше и будет гарантировать нам «полный обход» всех вершин графа. Этот список посещенных вершин я буду использовать в следующем методе.

Метод для получения новой «текущей» вершины:

private Vertex GetCurrent(List<Vertex> visitedVertices)         {             List<Vertex> validAndNotGoalNeighbors = new List<Vertex>();              foreach (Vertex v in visitedVertices)                 if (HasValidAndNotGoalNeighbors(v, out validAndNotGoalNeighbors))                     break;              // Если не нашлось ни одного подходящего соседа, значит мы дошли              // до целевой вершины. Алгоритм завершен             if (!validAndNotGoalNeighbors.Any())                 return null;              // Иначе находим и возвращаем соседа с минимальной меткой             double minLabel = validAndNotGoalNeighbors.Min(v => v.Label);             Vertex newCurrent = validAndNotGoalNeighbors.First(v => v.Label == minLabel);              return newCurrent;         }

И вот он!! Метод для поиска кратчайшего (оптимального) пути (и его длины):

public List<Point2D> FindShortestPathAndLength(Point2D startPoint, Point2D goalPoint, out double shortestPathLength)         {             shortestPathLength = 0.0;             // Стартовой вершине присваиваем нулевую метку             Vertex start = Vertices[startPoint.i, startPoint.j];             start.Label = 0.0;             // Целевую вершину пометим, что она целевая             Vertex goal = Vertices[goalPoint.i, goalPoint.j];             goal.IsGoal = true;             // Помечаем стартовую вершину как текущую             Vertex current = start;                // В этом списке будем копить посещенные вершины             List<Vertex> visitedVertices = new List<Vertex>();                while (current != null)             {                 // Находим подходящих (годных) соседей: которые еще не посещены, не являются препятствиями и т.п.                 List<Vertex> neighbors = GetValidNeighbors(current);                  foreach (Vertex neighbor in neighbors)                 {                     double currentWeight = current.Label + Weight(current, neighbor);                     if (currentWeight < neighbor.Label)                     {                         neighbor.Label = currentWeight;                         neighbor.CameFrom = current.Coordinate;                     }                                     }                  // После того как все подходящие соседи рассмотрены (им расставлены метки), помечаем текущую вершину как посещенную                 current.IsVisited = true;                 // и добавляем ее в список посещенных вершин                 visitedVertices.Add(current);                 // Используем этот список посещенных вершин для поиска новой текущей вершины                 current = GetCurrent(visitedVertices);             }              // В конце работы алгоритма в целевой вершине в свойстве Label будет находиться длина искомого пути             shortestPathLength = goal.Label;             // Основываясь на свойстве CameFrom сформируем и вернем сам искомый путь             return GetShortestPath(goal);         }

Следующий метод на основе свойства CameFrom класса Vertex «собирает» и возвращает нам искомый путь:

private List<Point2D> GetShortestPath(Vertex goal)         {             List<Point2D> path = new List<Point2D>();                          path.Add(goal.Coordinate);             Point2D cameFrom = goal.CameFrom;              while (cameFrom != null)             {                 Vertex vertex = Vertices[cameFrom.i, cameFrom.j];                 path.Add(vertex.Coordinate);                 cameFrom = vertex.CameFrom;             }              return path;         }

Надо заметить, что массив, содержащий координаты искомого маршрута будет сформирован «задом на перед». Т.е. первым элементом массива будут координаты целевой вершины, а последним элементом — координаты стартовой.

Ну вот, в принципе, и все!

Весь остальной код, классы и методы, — являются вспомогательными (вычисление двумерного Гауссиана, запись/чтение из файла и т.п.). Если Вы дошли до этого абзаца и хорошо понимаете, что происходит, остальную часть, я думаю, понять Вам не составит труда. Поэтому не буду на нем останавливаться, тем более что код подробно прокомментирован.

Стоит, наверное, все-таки упомянуть о двух перегруженных конструкторах класса Graph, один из которых инициализирует граф с помощью поверхности (для расчетов я использовал только Гауссиан, можете поиграться с другими поверхностями), а другой конструктор инициализирует граф с помощью матрицы из нулей и единичек (матрица-препятствий) для создания сложных лабиринтов.

Давайте наконец посмотрим на результаты!

Результаты расчетов. Простые препятствия

Начнем с простого примера. Создадим на сетке небольшое вертикальное препятствие, рисунок 4, и позволим алгоритму обойти его:

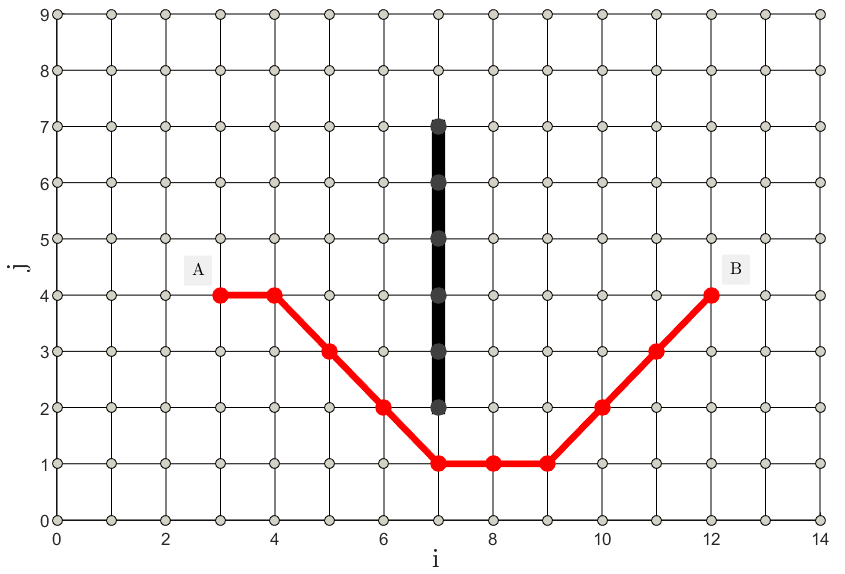
Вершины графа, которые попадают под черную линию имеют свойство IsObstacle = true, чтобы пометить их как вершины-препятствия. Параметр уклона MaxSlope здесь не имеет смысла, т.к. алгоритм работает в одной плоскости. Как видите, результат очень правдоподобный.

Из архива. Как я формировал это препятствие в csv-файле. Координаты пути

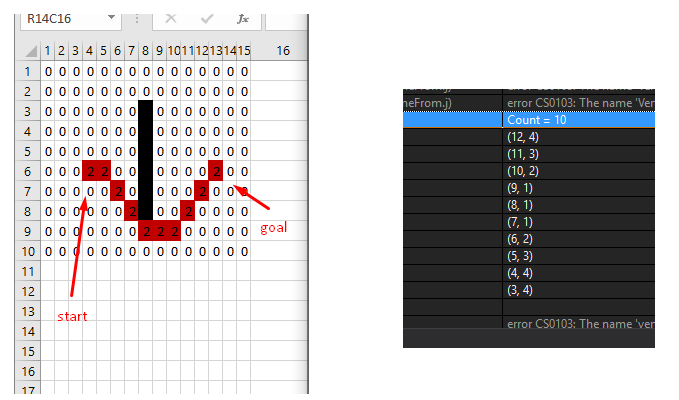
Для чтения матрицы из csv-файла и других вспомогательных действий создан класс Obstacle.

Рассмотрим следующий пример, рисунок 5:

В данном случае я бы не сказал, что это является ошибкой, ведь алгоритм учитывает как препятствие только те вершины графа, которые непосредственно помечены как вершины-препятствия (IsObstacle = true).

А вот если мы сформируем препятствие вот так, тогда алгоритм никуда не денется и ему придется его обойти, рисунок 6:

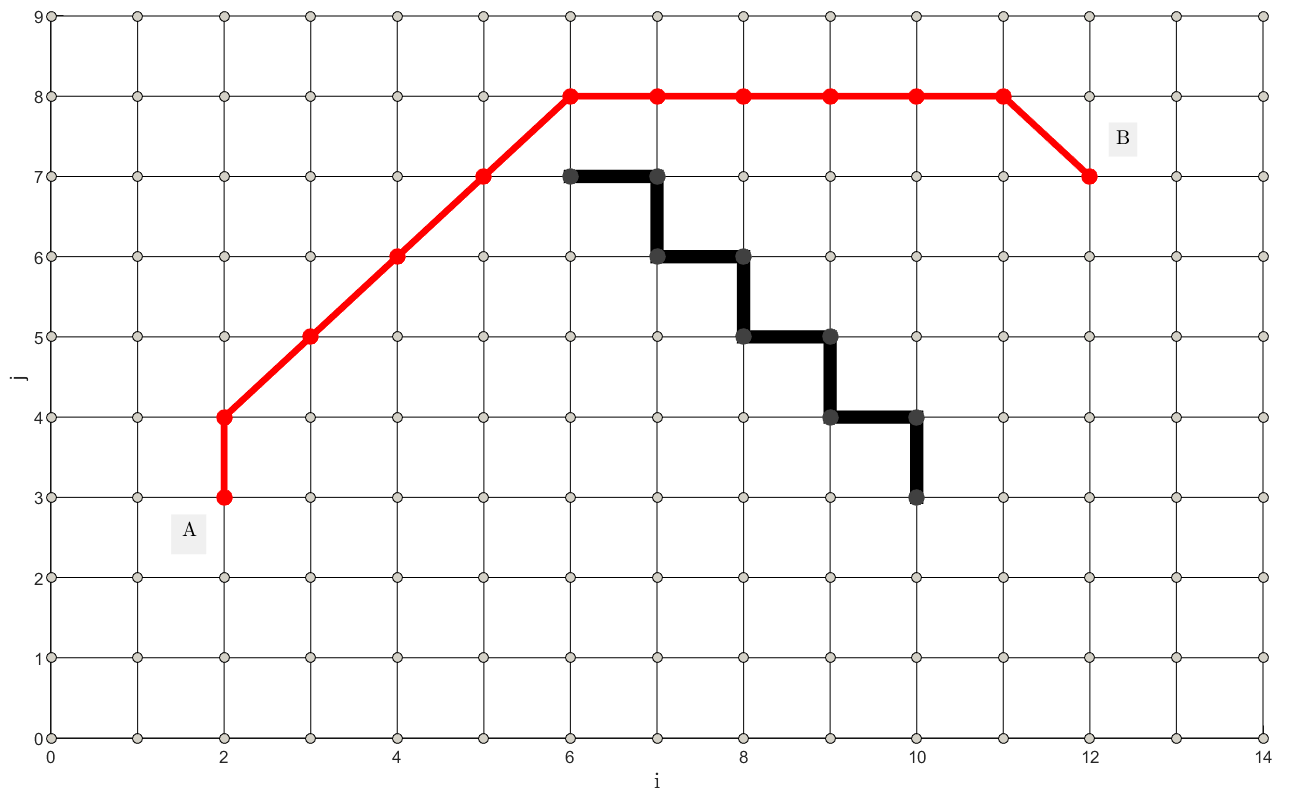
Лабиринты

Усложним работу для алгоритма и сформируем для него целый лабиринт препятствий, рисунок 7:

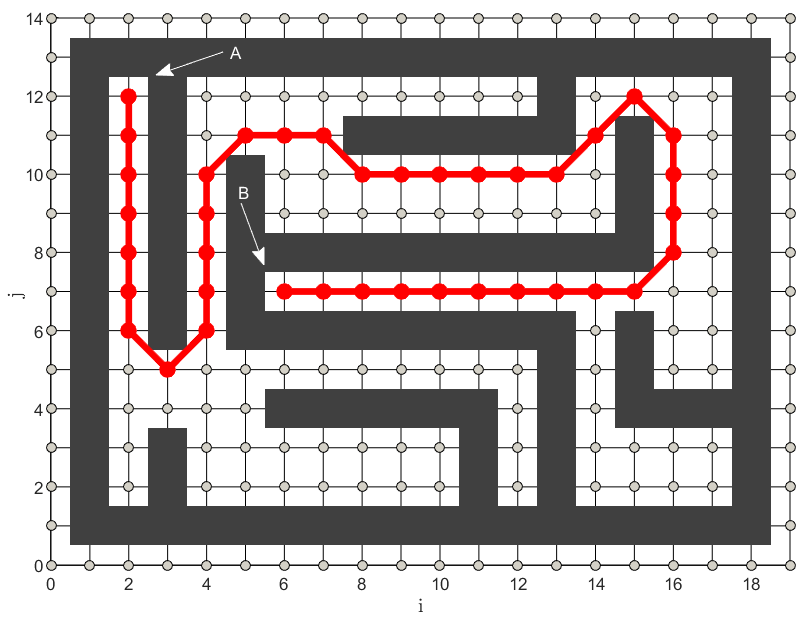
Увеличим лабиринт и изменим целевую вершину, рисунок 8:

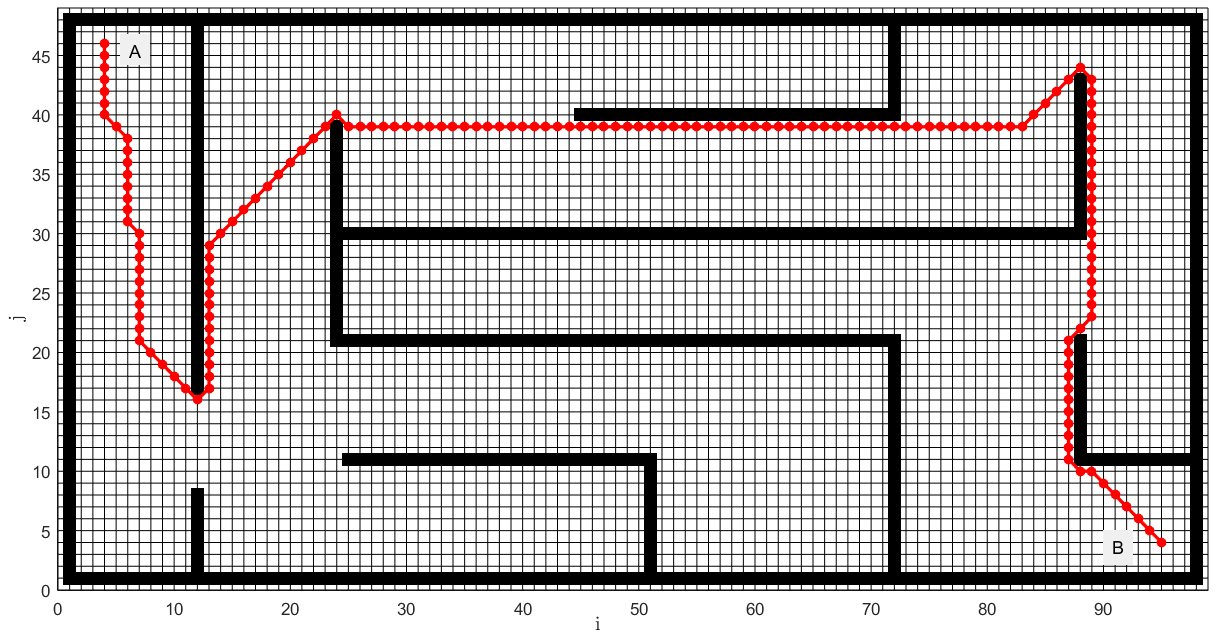
Все исходные файлы по которым были построены все вышеперечисленные препятствия и лабиринты, а также координаты найденных путей находятся в проекте в соответствующих папках.

Поиск оптимального пути на поверхности

Ну и в конце приведу пример поиска оптимального пути между двумя точками на сложной поверхности. Именно оптимального, т.к. нельзя сказать, что он кратчайший, рисунок 9:

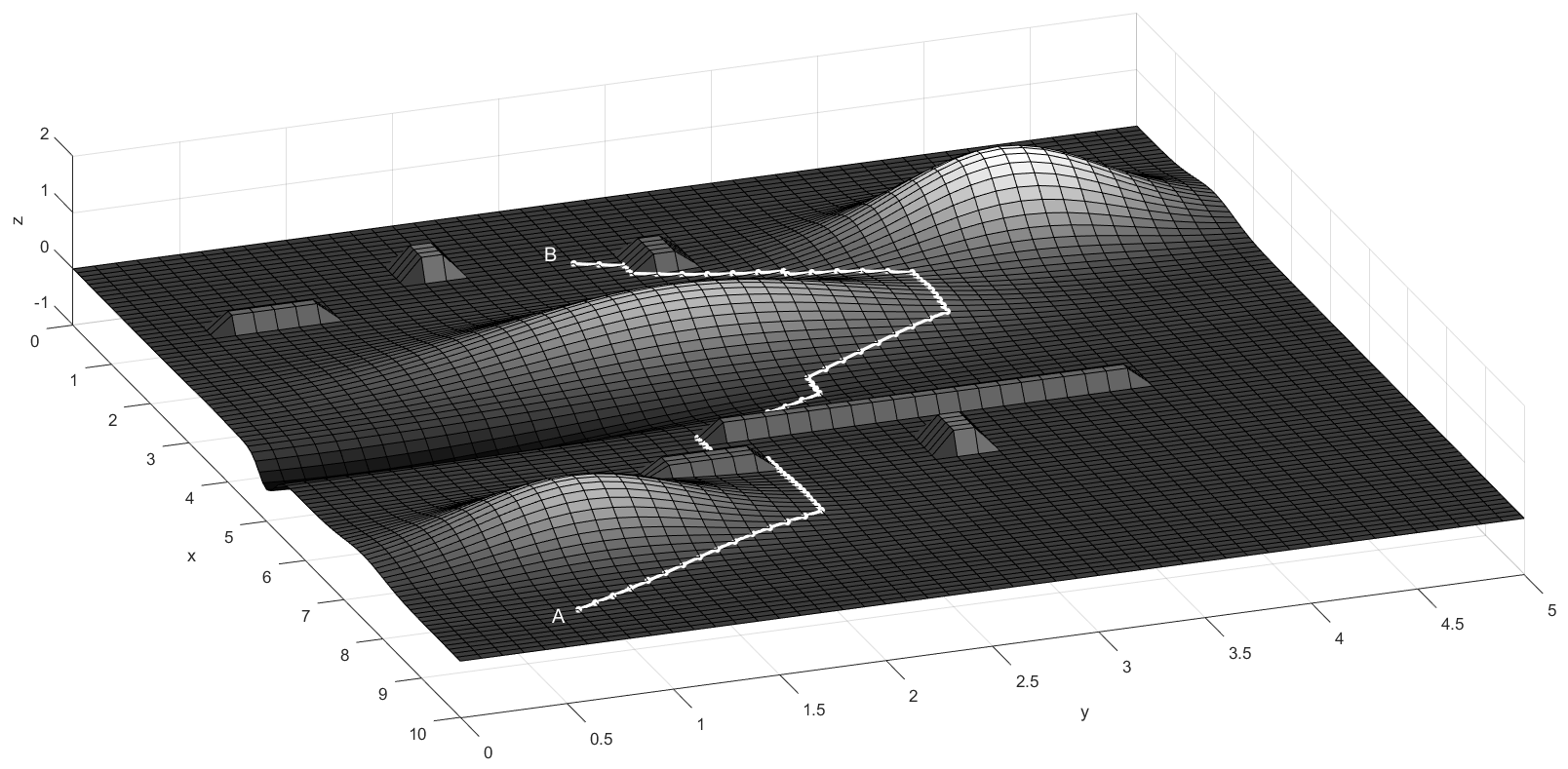
Для имитации холмов и оврага были использованы двумерные функции Гаусса с различными параметрами. Для имитации искусственных сооружений в класс Graph был добавлен метод:

public void CreateBuilding(Point2D bottomLeftCoordinate, int width, int length, double height)         {             for (int i = bottomLeftCoordinate.i; i < bottomLeftCoordinate.i + width; i++)             {                 for (int j = bottomLeftCoordinate.j; j < bottomLeftCoordinate.j + length; j++)                     Vertices[i, j].Height = height;             }         }

Замечу, что здесь ни одна вершина графа не помечена как препятствие, алгоритм находит оптимальный путь благодаря заданию параметра MaxSlope. Увеличивая этот параметр алгоритм может пойти прямиком через горы.

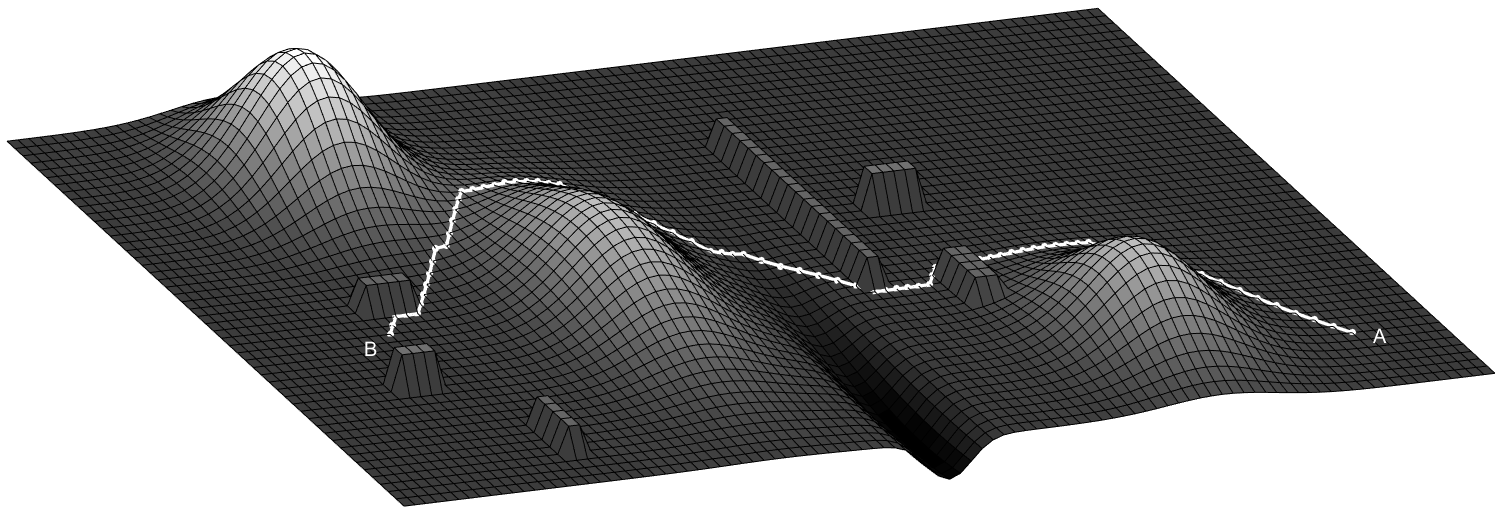
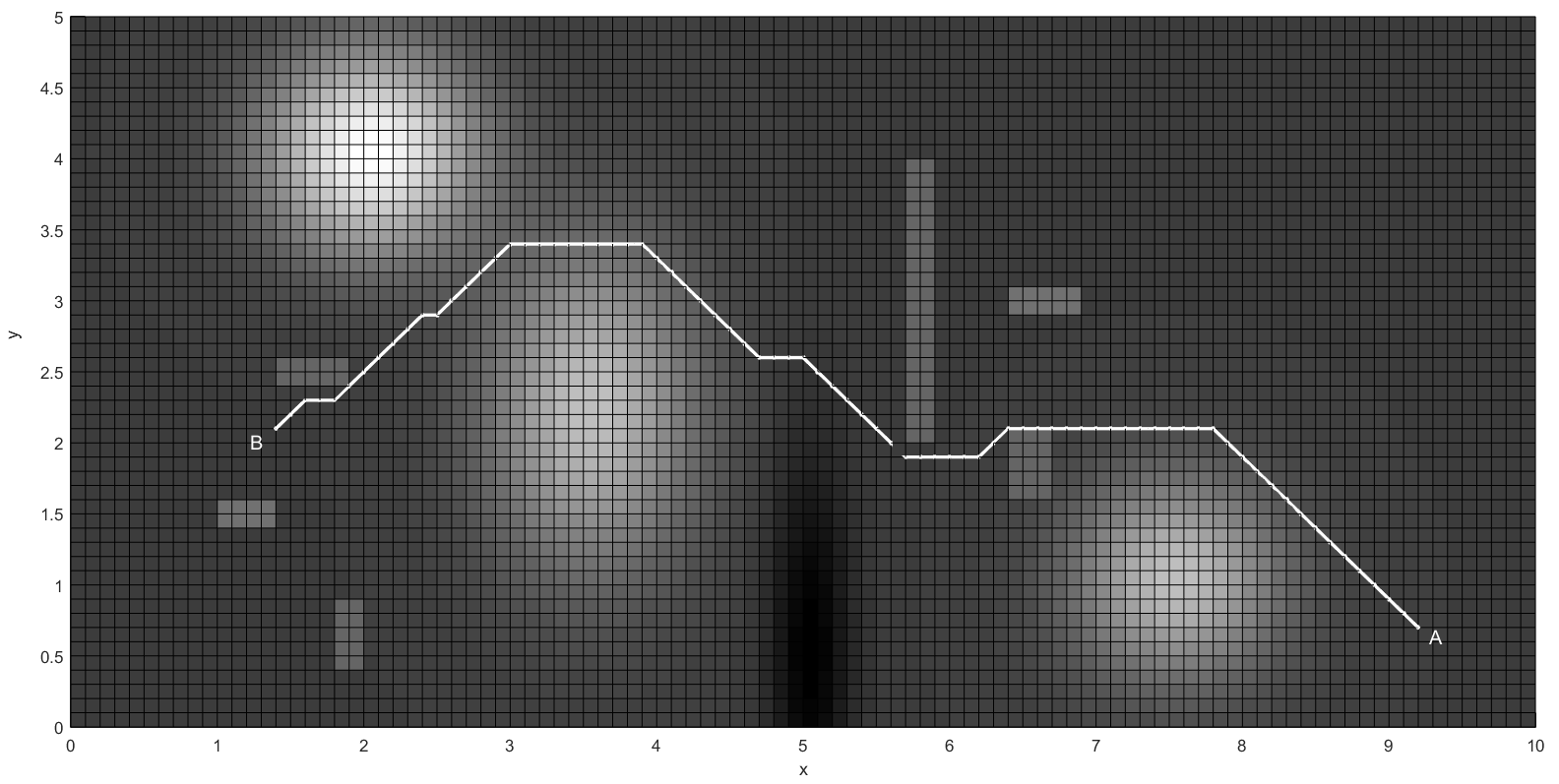
И еще картинки с других ракурсов.

Заключение

Спасибо за прочтение!

Надеюсь статья была интересной и полезной. Все доработки и оптимизацию алгоритма оставляю Вам.

Литература:

Робин Уилсон. Введение в теорию графов. Пятое издание. 2019

Всем добра и качественного кода!