Вычисление значения частоты любой ноты и интересное звучание «псевдонатурального» строя

Я занимаюсь написанием различных мелодий в разных жанрах довольно давно, но только недавно решил соотнести это занятие с научным подходом.

Что, если существует формула нахождения частоты любой выбранной ноты на любом аккорде? Что ж, углубившись в построение частот нот и настройку музыкальных инструментов, можно выяснить, что, во-первых, лучше использовать алгоритм, а во-вторых — всё будет зависеть от того, какой звукоряд используется:

На сегодняшний день, стандартом звукоряда является «равномерно темперированный строй«. В нём, ноты всех аккордов образуются от ноты «ля», а соотношение между соседними нотами всегда одинаковое: 1 делить на корень из двух по основанию 12. Значение частоты ноты «ля» в так называемой «первой октаве» (четвёртой по стандарту MIDI) равна 440 герц.

Не мала вероятность того, что вы натыкались на споры о частоте в 432 герца, мол она звучит лучше, что можно услышать от обычных людей, или же что она подсознательно воздействует на организм, лечит любые болезни, и вообще её поменяли, чтобы жили мы хуже, что можно услышать от скрывающихся от властей проповедников правды, которые живут по месту прописки.

А раньше — стандарта на частоту ноты «ля» вообще не было. Её настраивали по-разному для разных композиций и инструментов, что делало каждую мелодию более уникальной. Попробуйте сравнить ноты «ля» в современных мелодиях и на настоящих записях старых композиций: ноты в старых мелодиях зачастую будут звучать намного ниже, ибо частота часто была в районе 415-и герц.

Но просто менять частоту ноты «ля», и образовывать от неё другие — это скучно, ведь это почти равнозначно простому понижению питча итоговой мелодии. Что, если можно добиться очень необычного звучания? Например: поменять звукоряд.

Помимо «равномерно темперированного строя«, существует «натуральный строй«, в котором аккорды строятся иначе, а соотношение между нотами вообще сумасшедшие, но что главное — они могут быть не равны в разных аккордах, из-за чего вообще все и стали использовать «равномерно темперированный строй«. Не уверен, что такое подойдёт для современного композитора, ведь хочется иногда басовую партию прописать сначала на высоких частотах — прописал, сместил вниз, и получил кашу на выходе.

А что, если объединить строи, взяв из «равномерно темперированного строя» тот факт, что все ноты строятся от ноты «ля», а соотношения между нотами взять из «натуральный строя«? Правильно, получится какофония. Возможно, получатся удачные частоты для довольно необычных мелодий.

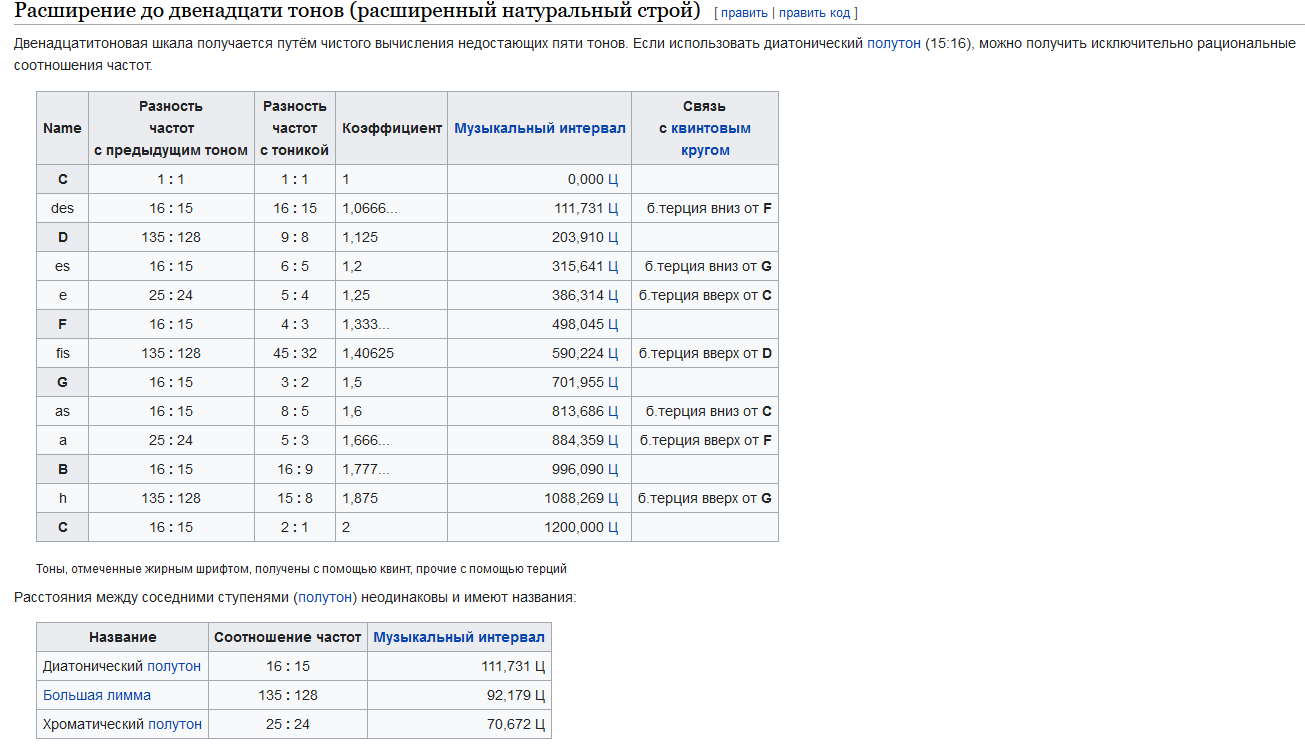
И так, теперь нужно написать программу, которая вычислит нам все частоты с довольно хорошей точностью, и выдаст их в виде массива дробных чисел.

Для начала нужно понять, какая будет частота ноты «ля» в субконтроктаве (нулевой аккорд по стандарту MIDI):

А соотношения можно взять обратные тем, что указаны на картинке немного выше.

Ну, и теперь можно продумать весь алгоритм:

база_ля          = 27.5 либо 25.9375 либо 27 колтчество_октав = 15 ноты_равномерные = [] ноты_натуральные = []   // Генерация нот в равномерном соотношении   // Можно заранее высчитать соотношения, ведь они одинаковые полтона_вверх = 1.0594630943592953 полтона_вниз  = 0.9438743126816934  // Основной цикл для "октава" в количестве "колтчество_октав":   ля = база_ля   умножаем ноту ля на два столько раз, какая сейчас октава - 1   // Теперь считаем ноты, одну за другой   ля_диез = ля * полтона_вверх   си = ля_диез * полтона_вверх   соль_диез = ля * полтона_вниз   соль = соль_диез * полтона_вниз   ...   до_диез = ре * полтона_вниз   до = до_диез * полтона_вниз   добавить все ноты в массив друг за другом, от "до" до "си"   // Генерация нот в натуральном соотношении, уже интереснее   для "октава" в количестве "колтчество_октав":   ля = база_ля   умножаем ноту ля на два столько раз, какая сейчас октава - 1   // И начинается самое интересное:   ля_диез = ля * (16/15) иррациональное значение   си = ля_диез * 1.0546875   соль_диез = ля * 0.96   соль = соль_диез * 0.9375   фа_диез = соль * 0.9375   фа = фа_диез * (128/135) иррациональное значение   ми = фа * 0.9375   ре_диез = ми * 0.96   ре = ре_диез * 0.9375   до_диез = ре * (128/135) иррациональное значение   до = до_диез * 0.9375   добавить все ноты в массив друг за другом, от "до" до "си"

Как можно заметить, все данные полностью совпадают с официальными, а даже если и не совпадают — то это потому что наш результат более точен, а в официальных данных приведены сокращённые значения.

Реализацию данного алгоритма я уже написал на языке программирования Python, с ней можно ознакомиться в моём репозитории на Codeberg (да здравствует свободное ПО!).

И рассчитав все ноты, получив их в виде массива, можно генерировать звуки нужных частот. Я даже написал программу всё на том же Python, которую можно найти во всё том же репозитории, и которая позволяет сыграть на MIDI клавиатуре мелодию «в любом строю», меняя его нажатием стрелочек «влево» и «вправо».

С частотой ноты «ля» в 415 герц и в «псевдонатуральном строю» ноты звучат словно на полтона ниже, но это не совсем так (что даже можно заметить), и звучат словно более эмоционально, более выразительно и душевно.

А для чего это я делал?

Разумеется, я начал этим увлекаться не просто так. У меня есть наполеоновские планы по созданию собственного, полностью свободного и кросс-платформенного аналога FLStudio, с удобным управлением и красивым дизайном, а не как это сделано в LMMS (без обид, но управление в нём очень кривое, и отвлекает от написания музыки). Я уже даже продумал, как будут устроены инструменты (не VST, но возможно даже лучше, и точно безопаснее, ибо я параноик, и хочу защитить пользователей от уязвимостей через инструменты).

И одной из главных особенностей моего аналога будет передача инструментам не только номера нажатой ноты по стандарту MIDI, но ещё и частоты, чтобы инструменты по большей части работали с частотами, и можно было добиваться необычных звучаний прямо во время написания.

Из проблем пока нерешённость, на чём лучше писать (пока что думаю на C++, с использованием мультимедиа библиотеки SFML), и как генерировать сами звуки, ибо у меня получается пока только шум, но по синусу улетающий в бесконечность. Вторая проблема решится подробным изучением принципов наложения разных волн разных частот для создания красивого звука и принципов работы с сэмплами. Будет сложно, особенно учитывая, что я не варился в музыкальной школе десять лет.

А для тех, кто был в музыкальной школе, и не мало — предлагаю писать в комментарии уточнения для данной статьи, а так же делиться своими необычными фактами. Думаю, многим будет интересно почитать.

А если вы шарите за разработку VST плагинов или вообще заинтересованы в написании свободного аналога FLStudio — можете связаться со мной, можно вместе что-нибудь обдумать.

Премного благодарен за выделенное внимание.