
Привет всем, добро пожаловать в раздел о сокращении Big O. В первой части мы познакомились с BigO нотацией, а сегодня вы узнаете, как взять большой сложный алгоритм и свести его до минимального значения Big O. После прочтения данной статьи вы сможете взглянуть на любой алгоритм и определить, что представляют собой различные компоненты в рантайме. Итак, давайте выясним, как на самом деле анализировать и определять Big O любого алгоритма.
Правила сокращения

Сначала мы отбрасываем неосновные термины, затем удаляем константы, затем добавляем любые доминирующие термины и умножаем любые вложенные.
Давайте посмотрим на несколько примеров:
func newFunc(_ n: Int) { var a = 0 a = 10 a += 5 // O(1) for i in 0..<n { i += 1 // O(n) } for _ in 0..<n { //some stuff... for _ in 0 <..n { //some stuff... // O(n^2) } } }Функции подобно этой состоят из различных частей.Здесь у нас есть константы, несколько простых операторов со временем выполнения O(n), а затем здесь вложенный цикл for, который является квадратичным. Если чложить их вместе, мы имеем выражение O(1), плюс O(n) плюс O(n^2), это время выполнения всего алгоритма. Но единственная часть, которая имеет значение и выполняет тяжелую работу, находится в конце — O(n^2). Это доминирующий термин. Когда мы уменьшаем сложность времени выполнения, мы говорим, что мы опускаем не доминирующие члены, в данном случае O (1) и O (n), и все это выражение просто сводится к O(n^2).
func newCondition(_n: Int) { if n == 5 { for_ in 0..<n { // Do some stuff... } else { for_ in 0..<n { // Do another stuff... for_ in 0..<n { // Do some stuff... } } } } }Теперь вам может быть интересно, а что, если у нас есть оператор if или какие-то условные выражения. В этом случае делаем то же самое, только берем наихудший случай. В этом примере, если у нас есть путь, которыйпровел бы нас по функции за скорость O(n), но есть и другой путь, который ведет сюда со скоростью O(n^2), это наихудший случай, потому что это доминирующий термин. Поэтому мы всегда берем наихудший случай, и это станет нашей сокращенной нотацией Big O для этого алгоритма.
func dropConstants(_n: Int) { for_ in 0..<n { //O(n) // Do stuff... } for_ in 0..<n { //O(n) // Do stuff... } for_ in 0..<n { //O(n) // Do stuff... } }Примером правила отбрасывания(сокращения) констант может быть подобный алгоритм с тремя циклами for, один за другим. Каждый из них мы можем сложить. У нас есть три O(n), что сводится к O(3n). Но на самом деле эта константа, тройка не имеет значение. Так что можем ее отбросить. И все это выражение сократится до O(n).
Теперь есть только две ловушки, с которыми мы должны быть осторожны при сокращении BigO.
func addDominants(_n: Int, _m: Int) { for_ in 0..<n { //O(n) // Do stuff... } for_ in 0..<m { //O(m) // Do stuff... } }Одна из них — сложение доминирующих терминов. Здесь у нас есть два цикла for. Обратите внимание, как один зацикливается O(n), а другой зацикливается O(m). Мы больше не можем их сократить. Поэтому, когда мы складываем эти два цикла, мы говорим, что время выполнения этого алгоритма составляет O (n + m). Это первый нюанс, с которым нужно быть осторожным.
func nested(_n: Int, _m: Int) { for_ in 0..<n { //O(n) // Do stuff... for_ in 0..<m { //O(m) // Do stuff... } } }То же самое относится и к вложенным циклам. У нас есть цикл for O(n), а затем внутри него еще один цикл for O(m), мы не можем объединить их в n в квадрате. На самом деле нам просто нужно объединить n в m. Таким образом, алгоритм сводится к O(n*m).
Упражнения
Теперь для проверки своих знаний предлагаю порешать немного задачек на сокращение алгоритмов:

Ответ
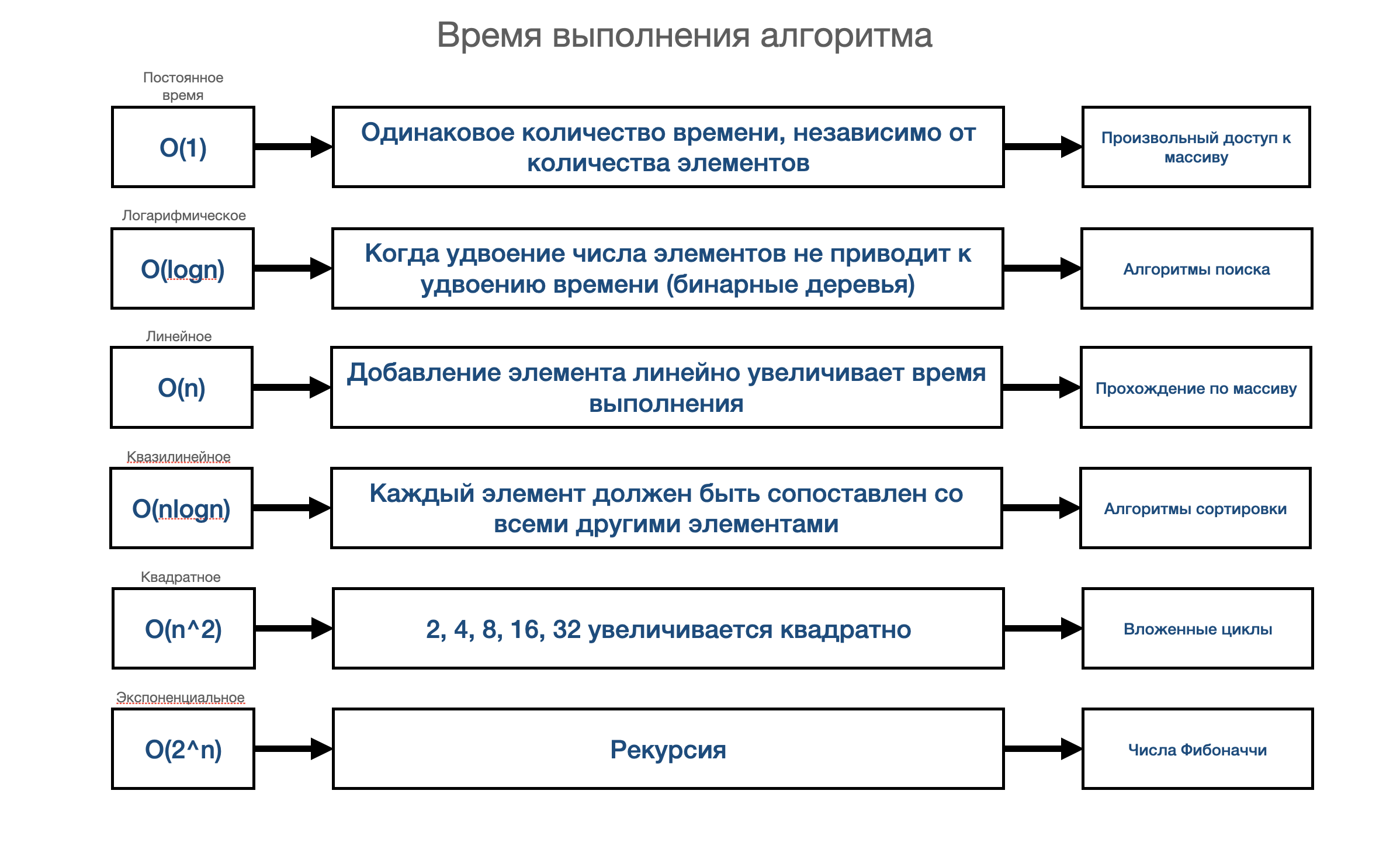
Смотрите на картинку подсказку в начале статьи чтобы найти доминирующие и не доминирующие алгоритмы
1) O(n) — «logn» не доминирующий и его можнос сократить
2)O(2^n) — сокращаем константы и не доминирующие алгоритмы и остается «2^n»

Ответ
1,2,3
4 вариант сократить нельзя
Заключение
Что касается собеседования, вам поможет в анализе алгоритмов:
Во-первых, понимание общих режимов выполнения
Во-вторых, знание, как определить время выполнения алгоритма( В основном: постоянные, логарифмические, линейные). И затем три, правила сокращения.
:
Помните о ловушках:

ссылка на оригинал статьи https://habr.com/ru/post/701822/
Добавить комментарий