Продолжая тему построение графических объектов используя мультимедийную библиотеку SFML, рассмотрим интересный класс VertexArray (массив вершин).
Точки
#include <SFML/Graphics.hpp> using namespace sf; int main() { srand(time(NULL)); RenderWindow window(VideoMode( 1500, 900 ), L"Titul", Style::Default); //Массив точек VertexArray mypoint(Points, 10000); for (int i = 0; i < 10000; i++) mypoint[i].position=Vector2f(rand()%1500, rand() % 900); while (window.isOpen()) { Event event; while (window.pollEvent(event)) { if (event.type == Event::Closed) window.close(); } window.clear(Color::Blue); window.draw(mypoint); // Точка window.display(); } return 0; }
VertexArray mypoint(Points, 10000) в параметрах объекта mypoint указываем тип объекта Points — точка и этих точек должно быть 10000. Через цикл for обращаемся к каждой точке и устанавливаем случайные координаты для неё mypoint[i].position=Vector2f(rand()%1500, rand() % 900), не забываем в начале запустить генератор случайных чисел srand(time(NULL)).
Линии
// Массив линий VertexArray myLines(Lines, 40); for (int i = 0,y=0; i < 40; i+=2,y+=10) { myLines[i].position = Vector2f(100, 100+y); myLines[i+1].position = Vector2f(500, 100+y); }
Объект myLines содержит в параметрах тип Lines — линия и количество точек 40, так как для построения линии необходимо две точки, указав 40 точек, получаем 20 линий. Как и ранее для каждой точки с помощью цикла for устанавливаем координаты места положения в графическом окне. Незабываем в конце цикла while (window.isOpen()) рисовать данный объект window.draw(myLines).
Ломаная линия
// Ломаная линия VertexArray myLinesStrip(LineStrip, 20); for (int i = 0, y = 0; i < 20; i += 2, y += 50) { myLinesStrip[i].position = Vector2f(600, 100 + y); myLinesStrip[i + 1].position = Vector2f(1200, 100 + y); }
Массив треугольников
// Массив треугольников VertexArray myTriangles(Triangles, 9); myTriangles[0].position= Vector2f(150, 350); myTriangles[1].position = Vector2f(250, 250); myTriangles[2].position = Vector2f(350, 350); myTriangles[0].color = Color(255, 0, 74); myTriangles[1].color = Color(255, 0, 74); myTriangles[2].color = Color(255, 0, 74); myTriangles[3].position = Vector2f(400, 200); myTriangles[4].position = Vector2f(600, 300); myTriangles[5].position = Vector2f(400, 400); myTriangles[3].color = Color(153, 255, 70); myTriangles[4].color = Color(153, 255, 70); myTriangles[5].color = Color(153, 255, 70); myTriangles[6].position = Vector2f(600, 400); myTriangles[7].position = Vector2f(800, 100); myTriangles[8].position = Vector2f(800, 400); myTriangles[6].color = Color(255, 255, 0); myTriangles[7].color = Color(255, 255, 0); myTriangles[8].color = Color(255, 255, 0);
Для отображения треугольников в параметрах объекта myTriangle указываем тип фигуры треугольник (Triangle) и обозначив 9 точек, рисуем три треугольника. Для корректного отображения фигур, необходимо следовать установленному порядку обозначения координат вершин треугольников.
Порядок определения координат вершин треугольников обозначен на рисунке №1.
Используя функцию Color разукрашиваем точки треугольников (myTriangles[8].color = Color(255, 255, 0)) в формате RGB.
Массив соединённых треугольников.
VertexArray myTriangleStrip(TriangleStrip, 10); myTriangleStrip[0].position = Vector2f(100, 200); myTriangleStrip[1].position = Vector2f(100, 400); myTriangleStrip[2].position = Vector2f(300, 200); myTriangleStrip[0].color = Color(0, 181, 99); myTriangleStrip[1].color = Color(0, 181, 99); myTriangleStrip[2].color = Color(102, 0, 99); myTriangleStrip[3].position = Vector2f(300, 400); myTriangleStrip[4].position = Vector2f(500, 300); myTriangleStrip[5].position = Vector2f(500, 500); myTriangleStrip[3].color = Color(102, 0, 99); myTriangleStrip[4].color = Color(255, 255, 0); myTriangleStrip[5].color = Color(255, 255, 0); myTriangleStrip[6].position = Vector2f(700, 300); myTriangleStrip[7].position = Vector2f(700, 500); myTriangleStrip[8].position = Vector2f(900, 400); myTriangleStrip[9].position = Vector2f(900, 600); myTriangleStrip[6].color = Color(126, 221, 54); myTriangleStrip[7].color = Color(126, 221, 54); myTriangleStrip[8].color = Color(0, 0, 205); myTriangleStrip[9].color = Color(0, 0, 205);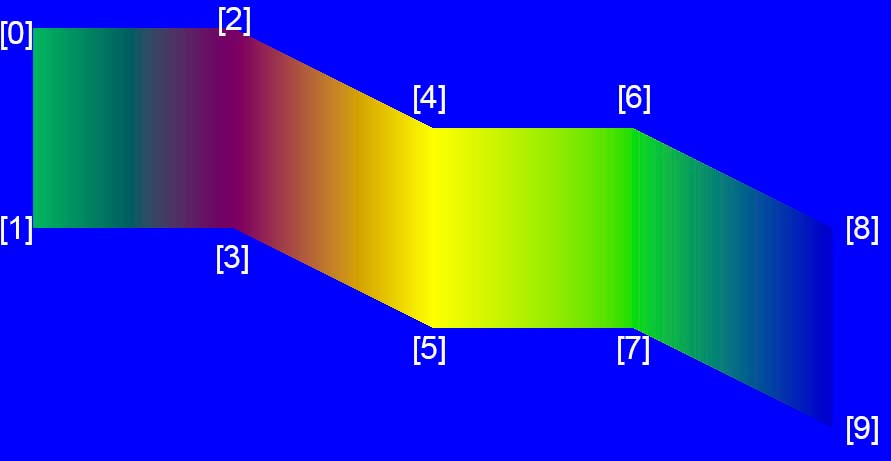
В массиве соединённых треугольников, каждый треугольник разделяет две свои последние вершины со следующим.
Массив треугольников соединённых с центральной точкой
VertexArray myTriangleFan(TriangleFan, 12); myTriangleFan[0].position = Vector2f(250, 200); myTriangleFan[1].position = Vector2f(350, 250); myTriangleFan[2].position = Vector2f(300, 300); myTriangleFan[0].color =Color::Yellow; myTriangleFan[1].color = Color::White; myTriangleFan[2].color = Color::White; myTriangleFan[3].position = Vector2f(250, 315); myTriangleFan[4].position = Vector2f(200, 300); myTriangleFan[5].position = Vector2f(140, 250); myTriangleFan[3].color = Color::Red; myTriangleFan[4].color = Color::Red; myTriangleFan[5].color = Color::Magenta; myTriangleFan[6].position = Vector2f(130, 200); myTriangleFan[7].position = Vector2f(140, 150); myTriangleFan[8].position = Vector2f(200, 100); myTriangleFan[9].position = Vector2f(250, 80); myTriangleFan[10].position = Vector2f(300, 100); myTriangleFan[11].position = Vector2f(350, 150); myTriangleFan[6].color = Color::Magenta; myTriangleFan[7].color = Color::Green; myTriangleFan[8].color = Color::Green; myTriangleFan[9].color = Color::Cyan; myTriangleFan[10].color = Color::Cyan; myTriangleFan[11].color = Color::Yellow;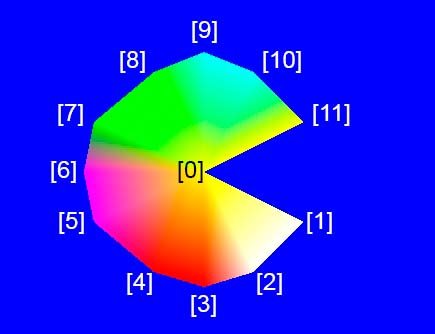
В массиве треугольников соединённых с центральной точкой первая вершина является центром, затем каждая новая вершина определяет новый треугольник, используя центр и предыдущую вершину.
Массив четырёхугольников
VertexArray myQuads(Quads, 12); myQuads[0].position = Vector2f(400, 300); myQuads[1].position = Vector2f(400, 200); myQuads[2].position = Vector2f(500, 200); myQuads[3].position = Vector2f(500, 300); myQuads[0].color = Color(255, 102, 255); myQuads[1].color = Color(255, 102, 255); myQuads[2].color = Color(255, 102, 255); myQuads[3].color = Color(255, 102, 255); myQuads[4].position = Vector2f(600, 300); myQuads[5].position = Vector2f(600, 200); myQuads[6].position = Vector2f(800, 200); myQuads[7].position = Vector2f(800, 300); myQuads[4].color = Color(102, 0, 99); myQuads[5].color = Color(102, 0, 99); myQuads[6].color = Color(102, 0, 99); myQuads[7].color = Color(102, 0, 99); myQuads[8].position = Vector2f(500, 500); myQuads[9].position = Vector2f(600, 400); myQuads[10].position = Vector2f(800, 400); myQuads[11].position = Vector2f(700, 500); myQuads[8].color = Color(255, 88, 0); myQuads[9].color = Color(255, 88, 0); myQuads[10].color = Color(255, 88, 0); myQuads[11].color = Color(255, 88, 0);
В массиве четырёхугольников, 4 вершины каждого четырёхугольника должны быть определены последовательно, либо по часовой стрелки, либо против часовой стрелки.
Прототип симулятора солнечной системы
Используя знания предыдущей и этой темы создадим симулятор солнечной системы.

В основе программного кода будем использовать формулу нахождения координат точки на окружности.
x = x0 + round(rad*cos(a*PI/180)); y = y0 + round(rad * sin(a * PI / 180))*vector;где, x и y — координаты вращающегося объекта, x0 и y0 — координаты центра вращения, round() — функция округления до ближайшего целого, rad — расстояние от центра вращения до объекта вращения, cos() и sin() — тригонометрические функции, a — изменяемый угол при вращении от 0 до 360 градусов, PI — число 3.14, vector — направление вращения равен 1 или -1. Процесс вычисления координат вращающегося объекта поместим в отдельный класс Planets. Который будет состоять из двух конструкторов:
Planets(int startx, int starty, int r, int v); Planets(int r, int v);где, переменные int startx, int starty — координаты центра вращения, int r — расстояние от центра вращения до объекта вращения, int v — направление вращения.
Методы int getx(), int gety() — будут возвращать координаты вращающегося объекта. Метод void move(double s) — будет изменять угол вращения с шагом указанным в переменной double s. Метод void setposition(int startx, int starty) служит для изменения центра вращения.
Ниже привожу код с подробным описание каждого блока.
#include <SFML/Graphics.hpp> #include <math.h> using namespace sf; using namespace std; // Класс для вычисления кооординат вращающегося объекта class Planets { public: Planets(int startx, int starty, int r, int v); Planets(int r, int v); int getx(); int gety(); void move(double s); void setposition(int startx, int starty); private: int x0=0,y0=0,rad=0,x=0,y=0,vector=1; double a = 0; const double PI = acos(-1.0); }; Planets::Planets(int startx, int starty, int r, int v) { if (v > 1) v = 1; if (v < -1 || v == 0) v = -1; vector = v; x0 = startx; y0 = starty; rad = r; } Planets::Planets(int r, int v) { if (v > 1) v = 1; if (v < -1 || v == 0) v = -1; vector = v; rad = r; } int Planets::getx() { return x; } int Planets::gety() { return y; } void Planets::move(double s) { a += s; if (a > 360) a = 0; x = x0 + round(rad*cos(a*PI/180)); y = y0 + round(rad * sin(a * PI / 180))*vector; } void Planets::setposition(int startx, int starty) { x0 = startx; y0 = starty; } int main() { // Запускаем генератор случайных чисел srand(time(NULL)); // Создаём графическое окно RenderWindow window(VideoMode(1500, 900), L"Солнечная система", Style::Default); // Вертикальная синхронизация кадров анимации window.setVerticalSyncEnabled(true); // Объявление планет солнце, меркурий, венера, земля, марс, луна CircleShape sun(100.f), merk(1), vener(6), earth(10), mars(4), moon(4); // Задаём параметры для солнца sun.setPosition(750, 450); sun.setOrigin(100,100); Texture texsun; texsun.loadFromFile("sun.png"); sun.setTexture(&texsun); //Задаём параметры для звезд VertexArray stars(Points, 50); for (int i = 0; i < 49; i++) {stars[i].color = Color(255, 255, 255); stars[i].position = Vector2f(rand() % 1500, rand() % 900);} //Задаём параметры для земли Texture texearth; texearth.loadFromFile("erd.png"); earth.setTexture(&texearth); earth.setOrigin(5,5); //Задаём параметры для венеры vener.setFillColor(Color(208, 159, 46)); vener.setOrigin(3, 3); //Задаём параметры для марса mars.setFillColor(Color(223, 54, 16)); mars.setOrigin(2, 2); //Задаём параметры для меркурия merk.setFillColor(Color(208, 159, 46)); //Задаём параметры для луны Texture texmoon; texmoon.loadFromFile("luna.png"); moon.setTexture(&texmoon); moon.setOrigin(2, 2); // Создаём объекты определения координат планет Planets merkxy(750,450,150,-1),venerxy(750,450,200,-1), marsxy(750,450,300,-1), earthxy(750,450,250,-1); Planets moonxy(30,-1); while (window.isOpen()) { Event event; while (window.pollEvent(event)) if (event.type == Event::Closed)window.close(); // Каждую итерацию изменяем угол положения планеты на 1 merkxy.move(1); //Устанавливаем текущие координаты объекта merk.setPosition(merkxy.getx(), merkxy.gety()); // Каждую итерацию изменяем угол положения планеты на 0.5 venerxy.move(0.5); //Устанавливаем текущие координаты объекта vener.setPosition(venerxy.getx(), venerxy.gety()); // Каждую итерацию изменяем угол положения планеты на 1.5 marsxy.move(1.5); //Устанавливаем текущие координаты объекта mars.setPosition(marsxy.getx(), marsxy.gety()); // Каждую итерацию изменяем угол положения планеты на 0.8 earthxy.move(0.8); //Устанавливаем текущие координаты объекта earth.setPosition(earthxy.getx(), earthxy.gety()); // Определяем центр вращения, так как земля меняет своё положение moonxy.setposition(earth.getPosition().x, earth.getPosition().y); // Каждую итерацию изменяем угол положения планеты на 3 moonxy.move(3); //Устанавливаем текущие координаты объекта moon.setPosition(moonxy.getx(), moonxy.gety()); // Вращаем солнце sun.rotate(-1); window.clear(); window.draw(stars); window.draw(sun); window.draw(merk); window.draw(vener); window.draw(earth); window.draw(mars); window.draw(moon); window.display(); } return 0; }Более подробную инструкцию по 2D примитивам мультимедийной библиотеки SFML вы можете увидеть посмотрев видео «2D примитивы SFML C++».
ссылка на оригинал статьи https://habr.com/ru/post/702128/
Добавить комментарий