Построение моделей на панельных данных в Python, часть 2: метод “разность разностей” (diff-in-diff)

Построение моделей на панельных данных в Python, часть 2: метод “разность разностей” (diff-in-diff).

Привет, Хабр! 

Данная статья является продолжением статьи “Построение моделей на панельных данных в Python, часть 1: объединенный МНК, модель с фиксированными эффектами, модель со случайными эффектами”. Напомню задачу: необходимо оценить, как изменились цены в отелях на островах Сардинии и Корсики после введения закона Макрона на острове Корсика.

Рассчитываем эффект воздействия методом разность разностей (diff-in-diff). Перед формальным описанием модели перечислю основные факторы, которые могут влиять на цену отеля:

• специфические особенности острова, в котором расположен отель (эффект острова);

• особенности различных периодов времени, например, изменение экономической конъюнктуры (временной эффект);

• эффект анонса закона Макрона (тот самый эффект, который мы пытаемся оценить). 

Формально можем записать так: Y_ist =α_s +μ_t +δ⋅D_ist +ε_ist, где индекс i — номер отеля, индекс s — остров (Корсика или Сардиния), индекс t — момент времени (период до анонса закона Макрона или период после него). Y_ist — цена отелей; переменная D равна 1 в отелях, которые находились на Корсике (и соответственно, на которые распространяется закон Макрона) и равно 0 во всех остальных случаях (если отели находились в Сардинии и на них закон Макрона не распространялся). α_s — эффект острова, он имеет два значения: αcontrol, если наблюдение относится к контрольной группе, т.е. к Сардинии; αtreatment, если наблюдение относится к испытуемой группе, т.е. к Корсике. μ_t — временной эффект. Он равен μ_before до анонса закона Макрона и μafter после анонса закона, δ — эффект воздействия анонса закона Макрона. Это тот самый эффект, который требуется оценить; ε_ist — случайные ошибки модели.

Подробные выкладки можно посмотреть в учебнике Картаева в главе 11[2].

Метод разности разностей непосредственно связан с оценкой моделей при помощи регрессий. Так как мы располагаем панельными данными об объектах из испытуемой и контрольной групп за два периода (до и после введения закона Макрона), оценка метода разности разностей может быть получена в результате применения следующей модели:

Y_it = β₀ + β₁ ⋅ X_i + β₂ ⋅ Z_t + δ ⋅ X_i ⋅ Z_t + ε_it, где X_i — бинарная переменная, которая равна единице, если i-й отель находится на Корсике, Z_t — бинарная переменная, которая равна единице для всех наблюдений, относящихся ко второму периоду (периоду после анонса закона).

Для состоятельности оценки требуется экзогенность объясняющей переменной. Если регрессор оказывается эндогенным из-за пропуска других существенных факторов, влияющих на Y, то эта проблема может быть решена включением в уравнение контрольных переменных.

Важная предпосылка метода разность разностей — параллельные претренды. Именно эта предпосылка позволяет предполагать, что за два периода t=0 и t=1 динамика Y (в нашем случае цены на отелей) в тритмент-группе, если бы она не подверглась воздействию, была бы такой же, как и динамика Y в контрольной группе. Проверим соблюдение этой предпосылки на наших данных.

Претренды показателя “средняя цена за неделю” сохраняются до вступления закона в силу сохраняются(см. Рисунок 2).

import matplotlib.pyplot as plt  trends= df.groupby(['week_number', 'region'], as_index=False).agg({'eurP': 'mean'}) trends['region'] = trends['region'].apply(lambda x: 1 if x == 'Corsica' else 0) fig, axes = plt.subplots(figsize=(9,6), dpi=80) plt.plot(trends[trends['region'] == 1]['week_number'], trends[trends['region'] == 1]['eurP'], label = 'о. Корсика', color = 'dodgerblue') plt.plot(trends[trends['region'] == 0]['week_number'], trends[trends['region'] == 0]['eurP'], label = 'о. Сардиния', color = 'deepskyblue') plt.axvline(x = 28, color = 'lightsteelblue', label = "Закон обнародовали") plt.axvline(x = 32, color = 'slategrey', label = "Закон вступил в силу") plt.legend() plt.xlabel('Номер недели', fontsize=12) plt.ylabel('Цена за 1 номер за 1 день, евро', fontsize=12) plt.title('Тренды средней цены на Корсике и в Сардинии', fontsize=14) plt.show()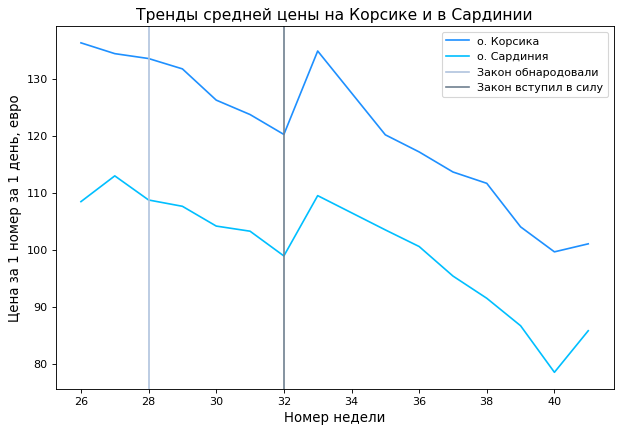

Рисунок 2: Тренды средней цены за неделю на Корсике и в Сардинии

Для построения моделей методом “разность разностей” добавим бинарные переменные.

def adding_dummies(df, col_names):     for column_name in col_names:         dummies =pd.DataFrame(pd.get_dummies(df[column_name],                                 prefix=column_name))         df=df.merge(dummies, left_index=True, right_index=True)     return(df)  df=adding_dummies(df, ['Star rating', 'Chain affiliation',                          'hot_size', 'region'])

И предобработаем данные следующим образом: если в модель мы добавим переменную PostLaw_Treated_NoChain, которая равна PostLaw* treat* Chain affiliation_0, то коэффициент при ней будет показывать насколько изменилась цена в отелях, которые “не сетевые”, на Корсике (где закон Макрона был принят) по сравнению с ценами в отелях, которые “не сетевые”, но уже в Сардинии (где закон не был принят). Введение таких новых переменных позволит нам сделать вывод об изменении цен в разрезе разных категорий.

df=df.rename(columns={'google_src': 'Google_Searchers',                        'town_avail': 'Hotel_availability'}) df['Postlaw_Treated']=df['postlaw']*df['treat'] df['PostLaw_Treated_NoChain']= df['postlaw']*df['treat']*df['Chain affiliation_0'] df['PostLaw_Treated_Chain']= df['postlaw']*df['treat']*df['Chain affiliation_1'] df['PostLaw_Treated_0stars']= df['postlaw']*df['treat']*df['Star rating_0'] df['PostLaw_Treated_1stars']= df['postlaw']*df['treat']*df['Star rating_1'] df['PostLaw_Treated_2stars']= df['postlaw']*df['treat']*df['Star rating_2'] df['PostLaw_Treated_3stars']= df['postlaw']*df['treat']*df['Star rating_3'] df['PostLaw_Treated_4stars']= df['postlaw']*df['treat']*df['Star rating_4'] df['PostLaw_Treated_5stars']= df['postlaw']*df['treat']*df['Star rating_5'] df['PostLaw_Treated_small_size']= df['postlaw']*df['treat']*df['hot_size_0'] df['PostLaw_Treated_medium_size']= df['postlaw']*df['treat']*df['hot_size_1'] df['PostLaw_Treated_large_size']= df['postlaw']*df['treat']*df['hot_size_2'] df['DaysCorsica']= df['bdays']*df['region_Corsica'] df['DaysSardinia']= df['bdays']*df['region_Sardinia'] df['const']=1

Строим модели. В модели добавляем контрольные переменные: количество дней с момента введения закона (DaysCorsica, DaysSardinia) для оценки долгосрочности эффекта, количество запросов в Google (Google_Searchers) и количество доступных отелей (Hotel_availability).

from linearmodels import IV2SLS from collections import OrderedDict from linearmodels.iv.results import compare  mod11v='lprice100 ~  Postlaw_Treated + DaysCorsica  + DaysSardinia  + Google_Searchers + Hotel_availability - 1' reg11v = IV2SLS.from_formula(mod11v,df).fit(cov_type="robust")  mod22v='lprice100 ~ PostLaw_Treated_NoChain + PostLaw_Treated_Chain + DaysCorsica  + DaysSardinia  + Google_Searchers + Hotel_availability - 1' reg22v = IV2SLS.from_formula(mod22v,df).fit(cov_type="robust")  mod33v='lprice100 ~  PostLaw_Treated_0stars + PostLaw_Treated_1stars + PostLaw_Treated_2stars + PostLaw_Treated_3stars + PostLaw_Treated_4stars + PostLaw_Treated_5stars + DaysCorsica  + DaysSardinia  + Google_Searchers + Hotel_availability -1' reg33v = IV2SLS.from_formula(mod33v,df).fit(cov_type="robust")  mod44v='lprice100 ~  PostLaw_Treated_small_size  + PostLaw_Treated_medium_size + PostLaw_Treated_large_size + DaysCorsica  + DaysSardinia  + Google_Searchers + Hotel_availability - 1' reg44v = IV2SLS.from_formula(mod44v,df).fit(cov_type="robust")  res1v = OrderedDict() res1v["D-in-D"] = reg11v res1v["Triple_Chains"] = reg22v res1v["Triple_Stars"] = reg33v res1v["Triple_Size"] = reg44v result = compare(res1v, stars=True, precision='std_errors') print(result)

Исходя из построенных моделей, мы можем сделать следующие выводы: 

• введение закона Макрона повышает цену отелей, так как коэффициент при Postlaw_Treated > 0. Но увеличение цены происходит только в краткосрочном периоде. С увеличением количества дней, которые прошли с момента введения закона (с 6 августа 2015 года) цена на отели снижается: коэффициенты при DaysCorsica и DaysSardinia отрицательные. Причем на Сардинии цены снижаются быстрее и краткосрочный рост цен на отели ниже, чем на Корсике, потому что коэффициент при DaysSardinia по модулю больше коэффициента при DaysCorsica.

• Цены на сетевые отели выросли больше, чем цены на несетевые отели, так как коэффициент при PostLaw_Treated_Chain > коэффициента при PostLaw_Treated_NoChain.

• Чем больше количество звезд у отеля, тем сильнее увеличилась цена после введения закона Макрона, кроме однозвездочных отелей — на них цена снизилась после введения закона (коэффициент при PostLaw_Treated_1stars < 0).

Результаты построения моделей методом разность разностей дали нам более содержательную интерпретацию, чем построение модели объединенного МНК, моделей с фиксированными и случайными эффектами.

Скачать код можно тут.

[1] Andrea Mantovani, Claudio A. Piga, Carlo Reggiani, Online platform price parity clauses: Evidence from the EU Booking.com case, European Economic Review, Volume 131, 2021, 103625, ISSN 0014-2921, https://doi.org/10.1016/j.euroecorev.2020.103625.

[2] Филипп Картаев “Введение в эконометрику”: учебник. – М.: Экономический факультет МГУ имени М.В. Ломоносова, 2019. – 472 с. ISBN 978-5-906932-22-8