На сегодняшний день сортировка является очень важной частью в любой системе баз данных. Речь идет о расположении данных в порядке возрастания или убывания. Мы используем сортировку для генерации последовательного вывода, а также для выполнения условий различных алгоритмов, работающих с базами данных. При обработке запросов для эффективного выполнения различных реляционных операций, таких как join и т. д., используются различные методы сортировки, потому что корректной работы большинства запросов системе необходимо предоставлять отсортированные входные данные. Если говорить о сортировке отношения, то мы должны построить индекс по сортировочному ключу и использовать этот индекс для считывания отношения в отсортированном порядке. Однако, используя индекс, мы сортируем отношение логически, а не физически. Таким образом, сортировка может столкнуться с двумя случаями:
Случай первый: Отношение имеет меньший размер в сравнении с доступной оперативной памятью.
Случай второй: Отношение превышает размер доступной оперативной памяти.
В первом случае отношения малого или среднего размера не выходят за рамки доступной оперативной памяти. Это значит, что мы можем полностью уместить их в оперативной памяти. Таким образом, в этом случае мы можем использовать стандартные методы сортировки, такие как quicksort, сортировка слиянием и т. д.
Во втором случае стандартные алгоритмы уже не будут работать корректно. Именно для таких отношений, размер которых выходит за рамки доступной оперативной памяти, мы используем алгоритм внешней сортировки слиянием (External Merge Sort).
Группа методов сортировки отношений, которые не помещаются в оперативную память из-за своего, в совокупности называется внешней сортировкой (External Sorting). Наиболее подходящим для этой задачи методом внешней сортировки является алгоритм внешней сортировки слиянием.
Алгоритм внешней сортировки слиянием (External Merge Sort)
Ниже мы подробно разберем все этапы алгоритма внешней сортировки слиянием:
M в алгоритме означает количество дисковых блоков, доступных в буфере оперативной памяти для сортировки.
Этап 1: Изначально мы создаем несколько отсортированных прогонов. Мы сортируем каждый из них. Эти прогоны содержат только часть записей отношения.
i = 0; repeat считываем либо М блоков, либо остаток отношения меньшего размера: сортируем часть отношения, размещенную в оперативной памяти; записываем отсортированные данные в файл Ri; i =i+1; until конец отношенияКак видите, на первом этапе мы выполняем операцию сортировки для отдельных дисковых блоков. Закончив с первым этапом, переходите к непосредственно ко второму.
Этап 2: На втором этапе мы объединяем прогоны. Учтите, что общее количество прогонов, т. е. N, должно быть меньше, чем M. Таким образом, мы можем аллоцировать в памяти один блок для каждого прогона, и там еще останется место для хранения одного блока вывода. Выполняем эту операцию следующим образом:
считываем один блок из N файлов Ri в буферный блок в оперативной памяти; repeat выбираем первый кортеж среди всех буферных блоков (выбор производится в порядке сортировки); записываем кортеж в вывод, а затем удаляем его из буферного блока; если буферный блок любого прогона Ri пуст и не EOF(Ri) тогда считываем следующий блок Ri в буферный блок; until все входные буферные блоки пусти После завершения второго этапа на выходе мы получим отсортированное отношение. Затем выходной файл буферизуется для минимизации операций записи на диск. Поскольку этот алгоритм производит слияние N прогонов, он известен как N-стороннее слияние (N-way merge).
Однако, если размер отношения больше объема допустимой памяти, то на первом этапе будет сгенерировано более M прогонов. Из-за этого будет невозможно выделить один блок для каждого прогона на втором этапе. В таком случае операция слияния выполняется в несколько проходов. Поскольку для M-1 входных буферных блоков памяти будет достаточно, каждое слияние может брать в качестве входных данных M-1 проходов. С этими изменениями алгоритм будет выглядеть следующим образом:
-
Он объединяет первые M-1 прогонов, чтобы получить один прогон для последующей обработки.
-
Точно так же он объединяет следующие M-1 прогонов. Этот шаг продолжается до тех пор, пока он не обработает все изначальные прогоны. Таким образом количество прогонов уменьшилось в М-1 раз. Тем не менее, если это уменьшенное значение больше или равно M, нам нужно сделать еще один проход. Для этого нового прохода входными данными будут прогоны, созданные первым проходом.
-
Работа каждого прохода будет заключаться в уменьшении количества прогонов в М-1 раз. Эта задача повторяется столько раз, сколько необходимо, пока количество прогонов не станет меньше или равно M.
-
Таким образом, последний проход даст нам отсортированный вывод.
Оценка стоимости метода внешней сортировки слиянием
Анализ стоимости внешней сортировки слиянием выполняется с использованием рассмотренных выше этапов алгоритма:
-
Предположим br обозначают количество блоков, содержащих записи отношения r.
-
На первом этапе он считывает каждый блок отношения и записывает их обратно. Всего потребуется 2br перемещений блоков.
-
Изначально значение количества прогонов равно [br/M]. Поскольку количество прогонов уменьшается на M-1 в каждом проходе слияния, требуется в общем [log M-1(br/M)] проходов слияния.
Каждый проход считывает и записывает каждый блок отношения только один раз. Но с двумя исключениями:
-
Последний проход может дать отсортированный вывод без записи результата на диск.
-
Могут быть шансы, что некоторые прогоны не будут прочитаны или записаны во время прохода.
Если пренебречь этими небольшими тонкостями, получается общее количество перемещений блоков для внешней сортировки:
b r (2 Γ log M-1 (b r /M) ˥ + 1)
Сюда также следует добавить стоимость поиска на диске, потому что каждый прогон предполагает поиск для чтения и записи данных. Если на втором этапе, т. е. на этапе слияния, каждому прогону выделяется bb буферных блоков или каждый прогон считывает bb данных за раз, то каждое слияние требует [br /bb] операций поиска для считывания данных. Вывод записывается последовательно, поэтому, если он находится на том же диске, что и входные прогоны, головке нужно будет перемещаться между записями последовательных блоков. Таким образом, нам нужно будет добавить 2[br /bb] операций поиска для каждого прохода слияния, и общее количество операций поиска будет следующим:
2 Γ b r /M ˥ + Γb r /b b ˥(2ΓlogM-1(b r /M)˥ — 1)
Таким образом, нам нужно рассчитать общее количество обращений к диску для анализа стоимости алгоритма внешней сортировки слиянием.
Пример внешнего алгоритма сортировки слиянием
Давайте рассмотрим работу алгоритма внешней сортировки слиянием, а также проанализируем стоимость внешней сортировки на примере.
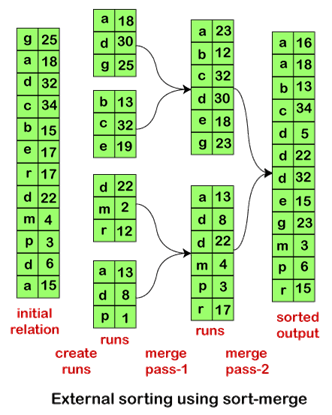
Допустим, мы выполняем внешнюю сортировку слиянием для отношения R. При этом предположим, что только один блок может содержать один кортеж, а память может содержать не более трех блоков. Таким образом, при обработке на втором этапе, то есть этапе слияния, он будет использовать два блока в качестве входных данных и один блок в качестве финального вывода.
Сегодня вечером в Otus состоится открытое занятие «Создание ассоциативного массива различными способами». На этом вебинаре мы реализуем структуру данных «ассоциативный массив» для хранения пар (ключ, значение). Рассмотрим несколько алгоритмов для решения этой задачи и сравним их эффективность:
-
односвязный список,
-
отсортированный массив,
-
двоичное дерево поиска,
-
хэш-таблица,
-
префиксное дерево.
Регистрация доступна на странице онлайн-курса «Алгоритмы и структуры данных».
ссылка на оригинал статьи https://habr.com/ru/company/otus/blog/712234/
Добавить комментарий