Предыстория

В предыдущей статье (Автоматический подбор синаптических весов. Самое начало. Циклический перебор) мы простым полным последовательным циклическим перебором подобрали коэффициенты для определения значения 13-ти сегментного индикатора.

Напомню результаты:

Начальная ошибка: 9.000000000000002 Начальная точность: 0.1  0: loss: 8.256888108456812 accuracy: 0.8 1: loss: 7.4035437200249845 accuracy: 0.8 2: loss: 6.515313270760133 accuracy: 0.8 3: loss: 5.655615573184693 accuracy: 0.8 4: loss: 4.889748309748125 accuracy: 0.9 5: loss: 4.243067834925036 accuracy: 0.9 6: loss: 3.6863744601447674 accuracy: 1.0 7: loss: 3.1957574183834616 accuracy: 1.0 8: loss: 2.7718738867787973 accuracy: 1.0 9: loss: 2.4043407365354073 accuracy: 1.0  Конечная ошибка: 2.4043407365354073 Конечная точность: 1.0

Полученные коэффициенты (синаптические веса):

[[ 0.2  0.6 -0.9  1.   1.  -0.4 -1.  -0.4  1.   0.5  0.6  0.4 -0.9]  [-1.  -1.   1.  -1.   1.  -1.  -1.   0.6 -1.   0.5 -1.  -1.   0.5]  [ 0.6  0.5 -0.6 -1.   1.   0.2  1.  -1.   1.  -1.   0.6  0.3 -0.6]  [ 0.1  0.9 -0.9 -1.   1.   0.7  0.9 -1.  -1.   1.   0.6  0.4 -1. ]  [ 0.8 -1.   0.3  1.   0.6  0.6  0.8 -1.  -1.  -0.2 -1.  -1.   0.5]  [ 0.2  0.6 -0.6  1.  -1.   0.5  0.7 -0.9 -1.   0.9  0.6  0.3 -0.7]  [ 0.1  0.7 -0.7  1.  -1.   0.2  1.  -0.8  1.   0.3  0.2  0.2 -0.6]  [ 1.   1.  -0.3 -1.   0.8 -1.  -1.   0.4 -1.   0.5 -1.  -1.   0.2]  [-0.6  0.8 -0.9  1.   1.  -0.3  1.  -1.   1.   0.7  0.3  0.2 -0.9]  [-0.6  0.7 -0.9  1.   1.   0.   0.9 -1.  -1.   0.8  0.7  0.6 -0.8]]

Графики:

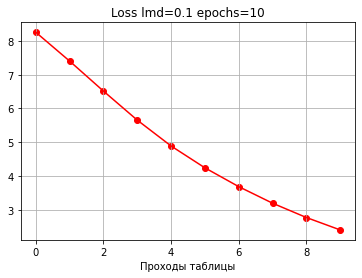
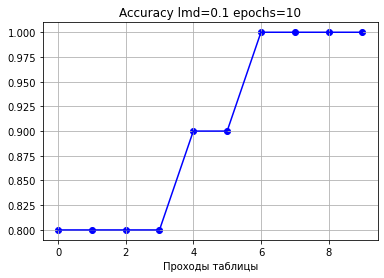
Еще раз обращаю внимание, почему выбран пример с 13-ти сегментным индикатором.

Действие алгоритма подбора принципиально не зависит от количества коэффициентов, разве что при большом количестве объектов и показателей очень захочется что-нибудь оптимизировать.

С точки зрения программирования и применения, в программу загружается набор данных, состоящий из показателей и классов объектов. Программа даже «не понимает», что это. Что именно — шахматы, кошечки, кредитные истории — не имеет значения. Можно сказать, что после подбора коэффициентов программа сообщает: «Примените данные коэффициенты к показателям и получите, к какому классу относится объект.» При этом программе так и «не знает», что это за объекты и кто и по какому принципу их разделил на такие классы.

Таблица коэффициентов для 13-ти сегментного индикатора состоит всего из 10 строк и 13 столбцов, ее легко представлять всю на экране и видеть глазами. Все изменения по ходу действия алгоритма можно реально наблюдать визуально. Если же брать, например, изображения рукописных цифр из набора MNIST, то там каждое изображение состоит из 28*28 = 784 пикселя, таблица будет содержать уже 784 столбца. Визуально уже сложно, хотя алгоритм будет тот же.

Таким образом изучаем алгоритм на примере 13-сегментного индикатора, и впоследствии можем работать с любым количеством коэффициентов в схожих задачах.

Циклический перебор

Кратко подбор коэффициентов простым полным последовательным перебором выглядит так (подробней об этом в прошлой статье):

1.       берем значение следующего коэффициента
2.       Считаем ошибку для текущего значения выбранного коэффициента
3.       Считаем ошибку для значения коэффициента, увеличенного на 1 шаг
4.       Считаем ошибку для значения коэффициента, уменьшенного на 1 шаг
5.       Определяем минимальную ошибку
6.       Фиксируем новое значение коэффициента
7.       Переходим на пункт 1.

Таким образом делаем 3 вычисления ошибки для каждого коэффициента и это повторяется многократно, по мере прохождения всей таблицы или достижения заданного уровня точности.

Посмотрим, как можно сократить количество вычислений, не ухудшая показатели точности.

Сокращение №1. Сохраняем минимальную ошибку.

Изначально мы делаем три подсчета ошибки для каждого коэффициента.

Заметим, что, полученное минимальное значение ошибки для текущего коэффициента будет значением начальной ошибки для следующего коэффициента. Если это значение сохранять, то высчитывать это значение для следующего коэффициента уже не понадобится. Таким образом количество вычислений ошибок для каждого коэффициента сократится с 3 до 2 — это 1,5 раза (!), а заменить нужно всего одну строку.

# базовый вариант  def choice():                                                                     # функция изменения коэффициентоа   this_array = np.zeros(3)                                                        # создаем нулевой массив для трех вариантов квадратической ошибки   this_array[0] = E()                                                             # считаем квадратическую ошибка с текущими кожффициентами      K_array[n][k] = np.round(K_array[n][k] + lmd,2)                                 # добавляем увеличиваем коффициенты на 1 шаг                                    this_array[1] = E()                                                             # считаем квадратическую ошибку с коэффициентами, увеличенными нв  1 шаг   K_array[n][k] = np.round(K_array[n][k] - 2*lmd,2)                               # уменьшаем коэффициенты на 1 шан   this_array[2] = E()                                                             # счиатаем квадратическую ошибку с кожффициентами, уменьшеными на 1 шаг   min = np.argmin(this_array)                                                     # выбираем минимальное значение квадратических шошибок   if min == 0: K_array[n][k] = np.round(K_array[n][k] + lmd,2)   if min == 1: K_array[n][k] = np.round(K_array[n][k] + 2*lmd,2)   return this_array[min]     

# Сокращение 1  def choice1():                                                                    # функция изменения коэффициентоа   this_array = np.zeros(3)                                                        # создаем нулевой массив для трех вариантов квадратической ошибки                                                     # создаем нулевой массив для трех вариантов квадратической ошибк   this_array[0] = last_E if N_epochs else E()                                     # присваиваем значение прошлых вычислений   K_array[n][k] = np.round(K_array[n][k] + lmd,2)                                 # добавляем увеличиваем коффициенты на 1 шаг                                    this_array[1] = E()                                                             # считаем квадратическую ошибку с коэффициентами, увеличенными нв  1 шаг   K_array[n][k] = np.round(K_array[n][k] - 2*lmd,2)                               # уменьшаем коэффициенты на 1 шан   this_array[2] = E()                                                             # счиатем квадратическую ошибку с кожффициентами, уменьшеными на 1 шаг   min = np.argmin(this_array)                                                     # выбираем минимальное значение квадратических шошибок   if min == 0: K_array[n][k] = np.round(K_array[n][k] + lmd,2)   if min == 1: K_array[n][k] = np.round(K_array[n][k] + 2*lmd,2)   return this_array[min]   

При запуске 100 раз на каждый вариант видим, что соотношение среднего времени действительно составляет 1.42, при том что итоговые коэффициенты, точность и ошибка остались теми же.

Начальная ошибка: 9.000000000000002 Начальная точность: 0.1  0: loss: 8.256888108456812 accuracy: 0.8 1: loss: 7.4035437200249845 accuracy: 0.8 2: loss: 6.515313270760133 accuracy: 0.8 3: loss: 5.655615573184693 accuracy: 0.8 4: loss: 4.889748309748125 accuracy: 0.9 5: loss: 4.243067834925036 accuracy: 0.9 6: loss: 3.6863744601447674 accuracy: 1.0 7: loss: 3.1957574183834616 accuracy: 1.0 8: loss: 2.7718738867787973 accuracy: 1.0 9: loss: 2.4043407365354073 accuracy: 1.0  Конечная ошибка: 2.4043407365354073 Конечная точность: 1.0  history  1000000100 1111110000 2222220222 1111111111 1111111111 1000022222 2222222222 2222000000 1111111111 1111010000 1111100100 1111000000 2222222202 2222222222 2222222222 1111111111 2222222222 1111111111 2222222222 2222222222 1111110000 2222222222 1111100000 2222222222 2222222222 1111100000 1111110000 1111100000 2222200002 2222222222 1111111111 1111000220 1111111111 2222222222 1111111111 2222222222 1111100100 1110000000 0222220200 1201000000 1111111011 2222222022 2222222222 1111111111 1111111000 1111110111 2222222222 2222222222 1111111111 1111101000 1111000000 2222222222 1111110101 2222222222 1011000000 1111111111 1111110000 1111101000 1111110110 2222222222 2222222222 1002220000 2222222222 2222222222 1101010001 1010000000 1111101000 2222202000 1111111111 2222222222 1111100000 1111111000 2222222022 2222222222 1111111011 1111100100 1110000000 2222220200 1201000000 1111111000 2222222000 1111111111 2222222222 1111100222 1111111111 2222222002 1111111111 1110010020 1101000200 1100000000 2222220000 1111111111 1111111111 2100002220 2222222222 1111101110 2222222222 2222222222 1110010000 2222222222 1111100000 2222222222 2222222222 1100000000 2222220000 1101111110 2222222220 1111111111 1111111111 1000002222 1111111111 2222222222 1111111111 0011111110 1111000020 1100000000 2222222202 2222220000 1111110010 2222222220 1111111111 1111111111 1101020022 1111111110 2222222222 2222222222 0011111111 1111111000 1111110000 2222222200  repeat: 1009 1170 86.24% norepeat: 161 1170 13.76%

choice [1.34516287 1.33209634 1.32759404 1.29756331 1.33321857 1.32479215  1.2962141  1.33684063 1.29419565 1.31248283 1.30394745 1.32590437  1.30781651 1.3311975  1.3117466  1.30371237 1.30382919 1.30745244  1.30841064 1.29821539 1.30923963 1.3346467  1.29679823 1.29549241  1.3124795  1.31248212 1.31808376 1.33855152 1.34169388 1.29907608  1.31198764 1.3170383  1.30334115 1.30047774 1.30835056 1.30654144  1.34071922 1.30453753 1.29899359 1.31498289 1.29986286 1.30740523  1.30502152 1.29074764 1.32386255 1.29606962 1.31344414 1.30162048  1.33640766 1.2925303  1.30747962 1.31347036 1.42314029 1.32453775  1.64896679 1.82337022 1.32944155 1.30337358 1.30806971 1.32695866  1.30223989 1.30760384 1.30920887 1.29674315 1.31281543 1.30356836  1.29090047 1.32715607 1.30350137 1.30583549 1.39502549 1.31496525  1.29643893 1.32158136 1.32618809 1.34265232 1.31811094 1.31174517  1.31136107 1.30955982 1.29934764 1.33040547 1.32615685 1.30861115  1.31614041 1.2995007  1.31219912 1.3024497  1.31846452 1.30366087  1.33307481 1.54476666 1.32489944 1.31990218 1.30798793 1.32574821  1.31216168 1.3218348  1.35234976 1.30790424] mean_choice: 1.326184549331665  choice1 [0.94452095 0.9373951  0.92703009 0.94945455 0.92299795 0.92515993  0.93847537 0.93791938 0.9218123  0.95027709 0.9208076  0.92714047  0.9368782  0.95326591 0.93058872 0.92267799 0.92855215 0.93107581  0.92012382 0.90938163 0.9526186  0.93981242 0.91682029 0.91633201  0.9254334  0.92791843 0.92099547 0.92510915 0.92451406 0.92016435  0.93162251 0.94082355 0.93707895 0.94391823 0.93335509 0.91597533  0.93292379 0.92699933 0.933285   0.93420839 0.93401527 0.9323349  0.94087124 0.92534971 0.93113422 0.92328262 0.94141126 0.9224  0.91569734 0.92672276 0.92225337 0.92245221 0.93381858 0.94988513  0.92701721 0.92473173 0.92835665 0.94492221 0.93563986 0.93288326  0.91142607 0.92793012 0.93967962 0.92340493 0.9515903  0.90949821  0.92115593 0.95414615 0.93081808 0.94648385 0.92893147 0.94108224  0.9197371  0.92430711 0.91657424 0.95124054 0.92906499 0.92733788  0.9328742  0.93052673 0.92267275 0.92845321 0.92182159 0.92123985  0.92826676 0.94259071 0.96250892 0.92144442 0.92686105 0.92599392  0.93305945 0.94481277 0.92452955 0.93930101 0.9549613  0.92280984  0.92588806 0.97600985 0.93930101 0.93104029] mean_choice1: 0.9316199898719788  1.4235252181674487

Сокращение №2. Сохраняем направление.

Анализ истории изменений коэффициентов показал, что в большинстве случаев направление движения сохраняется несколько шагов подряд, то есть вероятность того, что направление изменения на данном шаге будет такое же, как и на предыдущем больше, чем вероятность того, что направление изменится. В данном примере направление сохранялось в 86,24% случаев.

Исходя из представленного, каждый раз при оценке нужного изменения коэффициента мы можем предполагать, что, скорее всего, направление движения будем таким же, как и при предыдущем изменении этого коэффициента. Теперь будем брать из памяти направление движения и сразу считать ошибку именно для этого направления.

Если новая ошибка будет меньше сохраненной входящей, значит, изменение сделано корректно, сохраняем и переходим к следующему коэффициенту. Если же новая ошибка не будет меньше сохраненной входящей, то в этом случае вернем все обратно и сработаем по версии «Сокращение №1. Таким образом в большинстве случаев мы считаем лишь 1 ошибку и идем дальше. При этом итоговые коэффициенты, точность и ошибка остаются теми же, так как сами изменения делаются такими же.

def choice2():                                                                     # функция изменения коэффициентоа    if not N_epochs:                                                                  # здесь прошлого изменения еще нет, только начали      this_array = np.zeros(3)                                                        # создаем нулевой массив для трех вариантов квадратической ошибки     this_array[0] = last_E if N_epochs else E()                                     # считаем или скачиваем квадратическую ошибка с текущими кожффициентами      K_array[n][k] = np.round(K_array[n][k] + lmd,2)                                 # добавляем увеличиваем коффициенты на 1 шаг                                      this_array[1] = E()                                                             # считаем квадратическую ошибку с коэффициентами, увеличенными нв  1 шаг     K_array[n][k] = np.round(K_array[n][k] - 2*lmd,2)                               # уменьшаем коэффициенты на 1 шан     this_array[2] = E()                                                             # счиатем квадратическую ошибку с кожффициентами, уменьшеными на 1 шаг     min = np.argmin(this_array)                                                     # выбираем минимальное значение квадратических шошибок          if min == 0: K_array[n][k] = np.round(K_array[n][k] + lmd,2)     if min == 1: K_array[n][k] = np.round(K_array[n][k] + 2*lmd,2)     if min == 2: pass         if min == 0 : K_array_history[n][k] = K_array_history[n][k] + '0'     if min == 1 : K_array_history[n][k] = K_array_history[n][k] + '1'     if min == 2 : K_array_history[n][k] = K_array_history[n][k] + '2'      # Вносим K_array_history_last[n][k]. Это добавление по сравнения с Сокращеие №1          if min == 0 : K_array_history_last[n][k] = '0'     if min == 1 : K_array_history_last[n][k] = '1'     if min == 2 : K_array_history_last[n][k] = '2'       return this_array[min]                                                          # возвращает минимальное значение квадратической ошибки#     else:       this_array = np.zeros(3)                                                        # создаем нулевой массив для трех вариантов квадратической ошибки           # начинаем менять коэффициенты по прошлым изменениям          if K_array_history_last[n][k] == '0': pass             if K_array_history_last[n][k] == '1': K_array[n][k] = np.round(K_array[n][k] + lmd,2)     if K_array_history_last[n][k] == '2': K_array[n][k] = np.round(K_array[n][k] - lmd,2)      this_E = E()      if this_E < last_E:                                                             # если новое значение меньше, то идем дальше        K_array_history[n][k] = K_array_history[n][k] + K_array_history_last[n][k]       return this_E                                                                   # возвращает минимальное значение квадратической ошибки           else:                                                                            # если нет, то все возвращаем и пересчитываем          # вернули все обратно              if K_array_history_last[n][k] == '0': pass               if K_array_history_last[n][k] == '1': K_array[n][k] = np.round(K_array[n][k] - lmd,2)       if K_array_history_last[n][k] == '2': K_array[n][k] = np.round(K_array[n][k] + lmd,2)             this_array[0] = last_E                                                          # вместо вычислений берем уже сосчитанное знаяение ошибки значение ошибки               K_array[n][k] = np.round(K_array[n][k] + lmd,2)                                 # добавляем увеличиваем коффициенты на 1 шаг                                        this_array[1] = E()                                                             # считаем квадратическую ошибку с коэффициентами, увеличенными нв  1 шаг       K_array[n][k] = np.round(K_array[n][k] - 2*lmd,2)                               # уменьшаем коэффициенты на 1 шан       this_array[2] = E()                                                             # счиатем квадратическую ошибку с кожффициентами, уменьшеными на 1 шаг       min = np.argmin(this_array)                                                     # выбираем минимальное значение квадратических шошибок       #if n == 0 and k == 0: print(this_array, min)              if min == 0: K_array[n][k] = np.round(K_array[n][k] + lmd,2)       if min == 1: K_array[n][k] = np.round(K_array[n][k] + 2*lmd,2)       if min == 2: pass        if min == 0 : K_array_history[n][k] = K_array_history[n][k] + '0'       if min == 1 : K_array_history[n][k] = K_array_history[n][k] + '1'       if min == 2 : K_array_history[n][k] = K_array_history[n][k] + '2'        # Вносим K_array_history_last[n][k]. Это добавление по сравнения с Сокращеие №1              if min == 0 : K_array_history_last[n][k] = '0'       if min == 1 : K_array_history_last[n][k] = '1'       if min == 2 : K_array_history_last[n][k] = '2'         return this_array[min]   

100 запусков показывают, что соотношение с предыдущей версией составляет 1,2.

choice2 [0.77497625 0.77091789 0.7782073  0.7912941  0.75633955 0.77432227  0.76676011 0.77125525 0.74690795 0.76692891 0.78723669 0.76609111  0.76471782 0.76868224 0.76463151 0.76306868 0.75304341 0.77611017  0.76910067 0.75963497 0.76982474 0.77812576 0.77402616 0.76160932  0.77365232 0.77315974 0.78652763 0.77681923 0.75151467 0.77512097  0.78932977 0.76606202 0.76808095 0.76750255 0.76959753 0.75928688  0.75662851 0.77777982 0.78446841 0.77853799 0.75864053 0.75598574  0.7624383  0.7782011  0.76127625 0.76183152 0.80689144 1.30476522  1.04189086 0.78197837 0.75638342 0.76532078 0.74868345 0.76474953  0.76649427 0.77369595 0.75900817 0.7720716  0.77081013 0.7724154  0.77255964 0.75555062 0.77307916 0.79518604 0.76067805 0.76806164  0.77020645 0.7660327  0.75693035 0.75424552 0.77706718 0.76539826  0.75255966 0.77023005 0.76117682 0.76368403 0.78751493 0.75514174  0.75816417 0.76156425 0.76634574 0.76946759 0.75713634 0.76371884  0.757967   0.77221322 0.77076554 0.76274252 0.75766706 0.78485703  0.76216555 0.76573133 0.75066042 0.76631474 0.75741339 0.77243924  0.75984907 0.76662016 0.78093219 0.77088857]  mean_choice2: 0.7761234068870544  1.2003503329562035

Сокращение №3.

И теперь понимаем, что даже если новая ошибка не меньше входящей, то ошибка для коэффициентов без изменений у нас уже есть как входящая, ошибка для одного из направлений у нас только что посчитана, и нам остается посчитать только оставшуюся ошибку для оставшегося направления, что еще сокращает количество вычислений по сравнению с предыдущей версией. В итоге в большинстве случае мы считаем всего 1 ошибку и идем дальше, а если направление оказалось неправильным, то считаем всего еще 1 ошибку и идем дальше.

def choice3():                                                                     # функция изменения коэффициентоа   global repeat, norepeat     if not N_epochs:                                                                  # здесь прошлого изменения еще нет, только начали      this_array = np.zeros(3)                                                        # создаем нулевой массив для трех вариантов квадратической ошибки     this_array[0] = last_E if N_epochs else E()                                     # считаем или скачиваем квадратическую ошибка с текущими кожффициентами      K_array[n][k] = np.round(K_array[n][k] + lmd,2)                                 # добавляем увеличиваем коффициенты на 1 шаг                                      this_array[1] = E()                                                             # считаем квадратическую ошибку с коэффициентами, увеличенными нв  1 шаг     K_array[n][k] = np.round(K_array[n][k] - 2*lmd,2)                               # уменьшаем коэффициенты на 1 шан     this_array[2] = E()                                                             # счиатем квадратическую ошибку с кожффициентами, уменьшеными на 1 шаг     min = np.argmin(this_array)                                                     # выбираем минимальное значение квадратических шошибок     #if n == 7 and k == 7: print(N_epochs,n,k,this_array, min)     #if test and test[1] and test[2]:     #  if n == test[1] and k == test[2]: print(N_epochs,n,k,this_array, min)          if min == 0: K_array[n][k] = np.round(K_array[n][k] + lmd,2)     if min == 1: K_array[n][k] = np.round(K_array[n][k] + 2*lmd,2)     if min == 2: pass         if min == 0 : K_array_history[n][k] = K_array_history[n][k] + '0'     if min == 1 : K_array_history[n][k] = K_array_history[n][k] + '1'     if min == 2 : K_array_history[n][k] = K_array_history[n][k] + '2'      # Вносим K_array_history_last[n][k]. Это добавление по сравнения с Сокращеие №1          if min == 0 : K_array_history_last[n][k] = '0'     if min == 1 : K_array_history_last[n][k] = '1'     if min == 2 : K_array_history_last[n][k] = '2'       return this_array[min]                                                          # возвращает минимальное значение квадратической ошибки#     else:       this_array = np.zeros(3)                                                        # создаем нулевой массив для трех вариантов квадратической ошибки      #this_array[0] = last_E if N_epochs else E()                                     # считаем или скачиваем квадратическую ошибка с текущими кожффициентами            # начинаем менять коэффициенты по прошлым изменениям          if K_array_history_last[n][k] == '0': pass             if K_array_history_last[n][k] == '1': K_array[n][k] = np.round(K_array[n][k] + lmd,2)     if K_array_history_last[n][k] == '2': K_array[n][k] = np.round(K_array[n][k] - lmd,2)       this_E = E()         # новое меньше вхолящего. все ок. идем дальше     if this_E < last_E:                                                             # если новое значение меньше, то идем дальше       #if n == 7 and k == 7: print(N_epochs,n,k,'идем также',last_E,this_E, 'this_E < last_E', K_array_history_last[n][k] )       #if test and test[1] and test[2]:        # if n == test[1] and k == test[2]: print(N_epochs,n,k,'идем также',last_E,this_E, 'this_E < last_E', K_array_history_last[n][k] )         K_array_history[n][k] = K_array_history[n][k] + K_array_history_last[n][k]       repeat = repeat + 1       return this_E                                                                   # возвращает минимальное значение квадратической ошибки                   # нкжно проверить противоподожное и выбрать меньшее              if this_E >= last_E:                                                                            # если нет, то все возвращаем и пересчитываем         #if n == 7 and k == 7: print(N_epochs,n,k,'идем как-то по-другому',last_E_last,this_E)       #if test and test[1] and test[2]:        # if n == test[1] and k == test[2]: print(N_epochs,n,k,'идем как-то по-другому',last_E,this_E)                                                                                              # при этом 2 ошибки уже посчитаны, осталась только 1       # вернули все обратно              if K_array_history_last[n][k] == '0': pass               if K_array_history_last[n][k] == '1': K_array[n][k] = np.round(K_array[n][k] - lmd,2)       if K_array_history_last[n][k] == '2': K_array[n][k] = np.round(K_array[n][k] + lmd,2)            this_array[0] = last_E                                                          # вместо вычислений берем уже сосчитанное знаяение ошибки значение ошибки                                                                                                      # Сокращение 3 - это коррекция отсюда         if K_array_history_last[n][k] != '0':          #if n == 7 and k == 7: print(N_epochs,n,k,'идем как-то по-другому',last_E,this_E, 'прошлое не 0')             #if test and test[1] and test[2]:           #if n == test[1] and k == test[2]: print(N_epochs,n,k,'идем как-то по-другому',last_E,this_E, 'прошлое не 0')             #if N_epochs == (test[0]-1) and n == test[1] and k == test[2]: print('здесь должен быть приежним | ', K_array_3[test[1]][test[2]])                   if K_array_history_last[n][k] == '1':            this_array[1] = this_E           K_array[n][k] = K_array[n][k] = np.round(K_array[n][k] - lmd,2)           this_E_alt = E()           this_array[2] = this_E_alt           K_array[n][k] = K_array[n][k] = np.round(K_array[n][k] + lmd,2)          if K_array_history_last[n][k] == '2':            this_array[2] = this_E           K_array[n][k] = np.round(K_array[n][k] + lmd,2)             this_E_alt = E()           this_array[1] = this_E_alt           K_array[n][k] = K_array[n][k] = np.round(K_array[n][k] - lmd,2)         if K_array_history_last[n][k] == '0':           #if n == 7 and k == 7: print(N_epochs,n,k,'идем как-то по-другому',last_E,this_E, 'прошлое 0')          #if test and test[1] and test[2]:           #if n == test[1] and k == test[2]: print(N_epochs,n,k,'идем как-то по-другому',last_E,this_E, 'прошлое 0')                   K_array[n][k] = np.round(K_array[n][k] + lmd,2)                                 # добавляем увеличиваем коффициенты на 1 шаг                                          this_array[1] = E()                                                             # считаем квадратическую ошибку с коэффициентами, увеличенными нв  1 шаг         K_array[n][k] = np.round(K_array[n][k] - 2*lmd,2)                               # уменьшаем коэффициенты на 1 шаг         this_array[2] = E()                                                             # счиатем квадратическую ошибку с кожффициентами, уменьшеными на 1 шаг                    K_array[n][k] = np.round(K_array[n][k] + lmd,2)        min = np.argmin(this_array)                                                     # выбираем минимальное значение квадратических шошибок       #if n == 7 and k == 7: print(N_epochs,n,k,this_array, min)        #if test and test[1] and test[2]:         #if n == test[1] and k == test[2]: print(N_epochs,n,k,this_array, min)         # вот здесь при не равно 0 вытаскивается лишний шаг, так как он тянет из минуса              #if min == 0: K_array[n][k] = np.round(K_array[n][k] + lmd,2)       #if min == 1: K_array[n][k] = np.round(K_array[n][k] + 2*lmd,2)       #if min == 2: pass        # вот так работает при том, что чуть выше добавлена строка на возврат к предыдущему значению       if min == 0: pass       if min == 1: K_array[n][k] = np.round(K_array[n][k] + lmd,2)       if min == 2: K_array[n][k] = np.round(K_array[n][k] - lmd,2)        if K_array_history[n][k]:          if str(K_array_history[n][k])[-1] == str(min): repeat = repeat + 1         else: norepeat = norepeat + 1          if min == 0 : K_array_history[n][k] = K_array_history[n][k] + '0'       if min == 1 : K_array_history[n][k] = K_array_history[n][k] + '1'       if min == 2 : K_array_history[n][k] = K_array_history[n][k] + '2'        # Вносим K_array_history_last[n][k]. Это добавление по сравнения с Сокращеие №1              if min == 0 : K_array_history_last[n][k] = '0'       if min == 1 : K_array_history_last[n][k] = '1'       if min == 2 : K_array_history_last[n][k] = '2'         #if n == 7 and k == 7: print('возвращаем:', this_array[min])       #if test and test[1] and test[2]:         #if n == test[1] and k == test[2]: print('возвращаем:', this_array[min])              return this_array[min]    

100 запусков показывают, что ненамного, да улучшились. 1,05.

choice3 [1.03957939 0.73401165 0.74405241 0.78477812 0.74533463 0.72349954  0.74171138 0.73998713 0.72479033 0.75076938 0.74063039 0.73427916  0.72180223 0.73466134 0.73420072 0.74640346 0.76146626 0.75379515  0.7369113  0.72151875 0.72847867 0.73447752 0.75822163 0.7283318  0.7211144  0.71906424 0.71984696 0.7366631  0.73399925 0.72607017  0.71931577 0.76029229 0.74456286 0.71283984 0.72729754 0.73679471  0.73319244 0.73079419 0.73709345 0.76962519 0.74700379 0.72853994  0.72654438 0.73173642 0.73267102 0.7682457  0.73678899 0.73309374  0.73086071 0.74487996 0.73862243 0.72167659 0.72031069 0.73139524  0.73293161 0.71629572 0.74455285 0.72779083 0.73711133 0.72812796  0.723804   0.73224926 0.72075367 0.74264193 0.74765849 0.74866247  0.72236276 0.73962712 0.75126004 0.7156105  0.72916198 0.73277307  0.7307086  0.74466228 0.73302484 0.72850752 0.72256446 0.75273776  0.74249125 0.72412443 0.71607971 0.73670053 0.73501468 0.71607852  0.71313238 0.74638748 0.74781919 0.7494657  0.72298789 0.73058605  0.7420404  0.72067738 0.73757124 0.75603938 0.73866343 0.72893333  0.7308712  0.73227429 0.74706507 0.71966624]  mean_choice3: 0.7382487916946411  1.0513033216152954

Итог

В итоге 1.326184549331665 секунд превратились в 0.7382487916946411 секунд
Коэффициент 1.8.
На первый взгляд кажется, что 1,8 и ускорение на 0,59 секунд — это немного. Но ведь это лишь на 10 объектах и 13 показателях. При больших же датасетах вместо 10 часов получается 5 часов, вместо 2 дней получается 1 день, и это уже сильно заметно.

Предыдущие статьи:
Синаптические веса в нейронных сетях – просто и доступно. Часть 1.
Синаптические веса в нейронных сетях – просто и доступно. Часть 2.
Автоматический подбор синаптических весов. Самое начало. Циклический перебор

В следующих статьях предполагается протестировать простой полный последовательный циклический перебор с представленными варинтами на каком-либо публично известном датасете и переходить к дальнейшей оптимизации.