Основные приемы работы с Canvas [Part 2]

Привет! Мы продолжаем цикл статей по базовым принципам работы с canvas. Сегодня мы рассмотрим L-системы в качестве примера для создания различных интересных визуализаций.

Так что же такое L-ситемы? L-системы (или системы Линденмайера) — это набор простых правил, которые используются для моделирования роста водорослей (и не только), созданные венгерским биологом Аристидом Линденмайером в 1968 году.

В общем виде L-система представляет собой набор правил, применяемых к начальной строке, называемой аксиомой. Помимо этого система может содержать символы константы, на которые правила не распространяются. В самом простом виде правила могут быть описаны следующим образом:

Аксиома — «A»

Правило 1: «A» заменяется на «AB»

Правило 2: «B» заменяется на «B»

Природа таких систем рекурсивна и поэтому приводит к самоподобию, то есть к фракталам. В общем виде представление аксиомы для 5 поколения будет выглядеть так:

Значения аксиомы

n = 0: A

n = 1: AB

n = 2: ABA

n = 3: ABAAB

n = 4: ABAABABA

n = 5: ABAABABAABAAB

Давайте попробуем реализовать представленную выше систему правил для того, чтобы проверить, как ведет себя аксиома в коде:

let axiom = 'A';  const generation = 10; const rules = {   'A': 'AB',   'B': 'A' }  function applyRules(axiom) {   let result = '';    for (let char of axiom) {     result += rules[char];   }    return result; }  for (let i = 0; i < generation; i++) {   console.log(`generation ${i}: ${axiom}`);   axiom = applyRules(axiom) } 

Если мы посмотрим на получившиеся значения, то заметим, как быстро растет строка в каждом новом поколении:

Значения аксиомы для 10 поколений

generation 0: A

generation 1: AB

generation 2: ABA

generation 3: ABAAB

generation 4: ABAABABA

generation 5: ABAABABAABAAB

generation 6: ABAABABAABAABABAABABA

generation 7: ABAABABAABAABABAABABAABAABABAABAAB

generation 8: ABAABABAABAABABAABABAABAABABAABAABABAABABAABAABABAABABA

generation 9: ABAABABAABAABABAABABAABAABABAABAABABAABABAABAABABAABABAABAABABAABAABABAABABAABAABABAABAAB

Занимательный факт: если мы будем выводить не значение строки, а ее длину, то эти числа будут равны числам из последовательности Фибоначчи.

Черепашья графика

Так вот, для построения визуальной составляюшей L-систем обычно используется принцип черепашьей графики, который построен на идее существования указателя, который перемещается на заданное количество пикселей и угол и оставляет за собой шлейф.

Мы не будем сегодня рассматривать математику, которая лежит в основе черепашьей графики, так как это тема для отдельного урока, и в своих эксперементах будем использовать библиотеку better-turtle.

Давайте для начала разберем пример использования такой графики и нарисуем простой треугольник. Для этого устанавливаем библиотеку и проводим базовую настройку:

import { Turtle } from 'better-turtle';  const canvas = document.getElementById("canvas"); const ctx = canvas.getContext('2d');  canvas.width = window.innerWidth; canvas.height = window.innerHeight;  const turtle = new Turtle(ctx);

После устанавливаем толщину линии, а командой forward двигаем указатель на 300 пикселей вперед и по достижению целевой точки поворачиваем указатель на 120 градусов:

turtle.setWidth(5); turtle.right(90);  turtle.forward(300); turtle.left(120); turtle.forward(300); turtle.left(120); turtle.forward(300);

Получаем следующий результат:

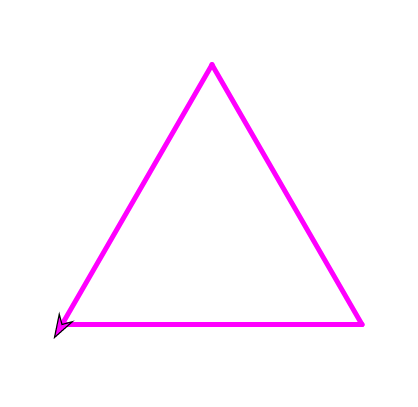
Давайте попробуем сделать еще что-нибудь. Для этого заведем цикл и на каждой итеррации будем поворачивать указатель на 90 градусов и сдвигать на постоянно растущий шаг:

let step = 0;  while (step < 400) {   turtle.forward(step);   turtle.right(90);   step += 20; }

В результате получим интересную спираль:

Применение черепашьей графики в L-системах

Интерпретацию описанной выше L-системы в черепашьей графике опишем в следующем виде:

«A» — поворот налево на 60 градусов и перемещение на расстояние step

«B» — поворот направо на 60 градусов и перемещение на расстояние step

Для начала сформируем аксиому для заданного поколения, немного модернизировав наш код:

function getAxiom(generation, axiom) {   for (let i = 0; i < generation; i++) {     axiom = applyRules(axiom);   }    return axiom; }

После реализуем метод создания черепашки, в котором зальем фон черным цветом и выставим толщину линии:

function createTurtle() {   const canvas = document.getElementById("canvas");   const ctx = canvas.getContext("2d");    canvas.width = window.innerWidth;   canvas.height = window.innerHeight;    const turtle = new Turtle(ctx);    ctx.fillStyle = "black";   ctx.fillRect(0, 0, canvas.width, canvas.height);    turtle.setWidth(3);    return turtle; }

Осталось только реализовать функцию отрисовки, в которой будем формировать аксиому для заданного поколения и отрисовывать согласно описанным выше правилам:

function draw() {   const turtle = createTurtle();    axiom = getAxiom(generation, axiom);    for (let char of axiom) {     if (char === "A") {       turtle.left(angle);       turtle.forward(step);     } else if (char === "B") {       turtle.right(angle);       turtle.forward(step);     }   } }

При step = 40, angle = 60 и generation = 14 получаем следующий результат:

Судя по рекурсивной природе L-систем, множество малых многоугольников будут формировать один большой. Таким образом, повышая поколения, мы можем получить большой многоугольник. Однако стоит учесть, что значение аксиомы растет очень быстро, как и число вычислений.

Треугольник Серпинского

Давайте теперь рассмотрим другой набор правил и попробуем получить треугольник Серпинского. Для этого возьмем следующий набор правил:

Переменные: F и G

Константы: + и —

Стартовая аксиома: F

Правило 1: «F» — F-G+F+G-F

Правило 2: «G» — G-G

Здесь F и G обозначает рисование отрезка, + — поворот угла направо и — — поворот угла налево на 120 градусов.

Изменим функцию применения правил, чтобы учесть константные значения:

function applyRules(axiom) {   let result = "";    for (let char of axiom) {     const rule = rules[char];     result += rule != null ? rule : char;   }    return result; }

И перепишем главный цикл под новые правила, где char1 и char2 — это F и G соответственно:

function draw() {   const turtle = createTurtle();    axiom = getAxiom(generation, axiom);    for (let char of axiom) {     if (char === char1 || char === char2) {       turtle.forward(step);     } else if (char === "+") {       turtle.right(angle);     } else if (char === "-") {       turtle.left(angle);     }   } }

В результате получаем треугольник Серпинского:

Это фрактал, двухмерный аналог множества Кантора. Реализация получения треугольника Серпинского через L-систему — очень интересная задача, поскольку обычно получают его методом хаоса.

Кривая дракона

Теперь получим другую интересную кривую, которая называется кривая дракона. Для этого определим новые правила следующего вида:

Переменные: X и Y

Константы: F, + и —

Стартовая аксиома: FX

Правило 1: «X» — X+YF+

Правило 2: «Y» — -FX-Y

Здесь X и Y обозначают рисование отрезка, + — поворот угла направо и — — поворот угла налево на 120 градусов.

В результате получаем интересную кривую под названием дракон Хартера-Хейтуэя:

Снежинка Коха

Для визуализации снежинки Коха зададим следующий набор правил:

Переменные: F

Константы: F, + и —

Стартовая аксиома: F++F++F

Правило 1: «F» — F-F++F-F

Здесь F обозначает рисование отрезка, + — поворот угла направо и — — поворот угла налево на 60 градусов.

В результате получим следующие снежинки для первого, второго и третьего поколений:

Снежинки Коха

Данная фрактальная кривая примечательна тем, что это кривая бесконечной длины. Однако есть еще более интересный вид правил: так называемые L-системы со скобками. Такие системы позволяют строить растения, которые выглядят очень реалистично.

L-системы со скобками

Для реализации L-системы со скобками зададим следующий набор правил:

Переменные: X и F

Константы: [, +, ] и —

Стартовая аксиома: X

Правило 1: «X» — F[+X]F[-X]+X

Правило 2: «F» — FF

Здесь X и F обозначают рисование отрезка, [ — соответствует сохранению текущих значений позиций и угла, которые восстанавливаются, когда появляется символ ], + — поворот угла направо и — — поворот угла налево на 22.5 градусов.

Для реализации подобных правил нам нужно внести некоторые изменения в код, а именно реализовать стек для выполнения условия со скобками. В случае, когда символ равен [, мы будем сохранять текущую позицию и угол и при появлении символа ] будем восстанавливать позицию. Таким образом, основной цикл примет вид:

function draw() {   const turtle = createTurtle();    axiom = getAxiom(generation, axiom);    for (let char of axiom) {     if (char === char1 || char === char2) {       turtle.forward(step);     } else if (char === "+") {       turtle.right(angle);     } else if (char === "-") {       turtle.left(angle);     } else if (char === "[") {       stack.push({         position: turtle.position,         angle: turtle.angle,       });     } else if (char === "]") {       const state = stack.pop();       turtle.setAngle(state.angle);       turtle.putPenUp();       turtle.goto(state.position.x, state.position.y);       turtle.putPenDown();     }   } }

В результате получим изображение, которое очень близко напоминает укроп:

Итого: мы получили довольно интересные визуализации, а также узнали, что такое L-системы и черепашья графика.

В дальнейших статьях мы рассмотрим принципы создания сцен и анимацию спрайтов, а также немного поговорим о шейдерах. До скорых встреч!