Взяться за статью меня побудил недавний (в исторических масштабах) эксперимент по сжатию изображений при помощи Stable Diffusion. Бегло прочесав азбучные истины вроде Википедии, я обнаружил, что проблема «красивой, но полностью выдуманной картинки» уже известна, но самое очевидное решение из приходящих в голову — по какой-то причине не фигурирует в них.
Причины, которые я могу предположить — оно или уже давно отброшено как неэффективное (слишком снижающее степень сжатия), или же не проработано, как имеющее слишком много вариаций, из которых «не все йогурты одинаково полезны».
К счастью, статья предназначена для «песочницы», поэтому я могу спокойно высказать собственные соображения — прежде, чем она отнимет чьё-то внимание, она должна получить одобрение более осведомлённых специалистов.
Проблема нейросетей, обучаемых передавать изображение через «бутылочное горлышко», свойственна и естественным нейросетям.
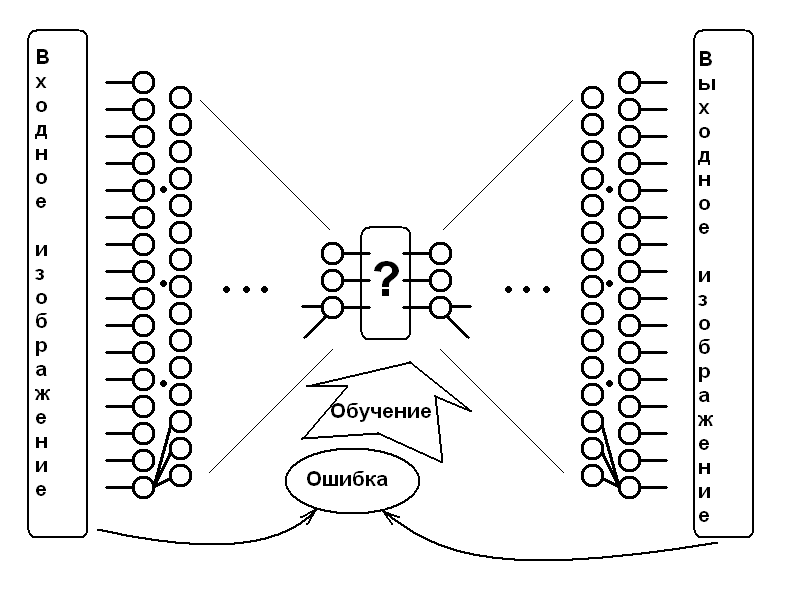
Многие родители, отпустившие «на самотёк» детей сходного возраста, быстро обнаруживают, что те выработали свой «детский язык», понятный только им. Причём, очевидно, дальше названий игрушек и прочего элементарного быта развитие этого «языка» не заходит, так что, даже если бы и захотелось, для полноценной жизни такой язык был бы слабо пригоден (оставим за бортом догадки, насколько сильно он может или не может развиться за тот период, когда человек к этому способен). Проблема решается радикально — детей переучивают на общепринятый язык, причём иногда это бывает уже довольно затруднительно. То же самое решение просится и тут: вместо «детского языка», который взаимно друг для друга придумали левая и правая половина нейросети для общения через «бутылочное горлышко» (обозначенного жирным знаком вопроса), отказаться от латентного пространства параметров вовсе, как и от правой половины нейросети. Просто взять и использовать в качестве целевого «языка», на который обучается сжимающая нейросеть, некий детерминированный формат сжатия, который легко подвергнуть декомпрессии обычной математикой (без нейросетей), но компрессия его настолько нетривиальна, что только достаточно мощная нейросеть способна решить эту задачу (на самом деле у меня почему-то есть уверенность, что до этого момента я излагал нечто очевидное и общеизвестное, но в комментариях к более свежим статьям навскидку ни у кого примеров не нашлось, так что вдруг…) Ну, а теперь переходим к нюансам, ради которых я и пишу эту статью.
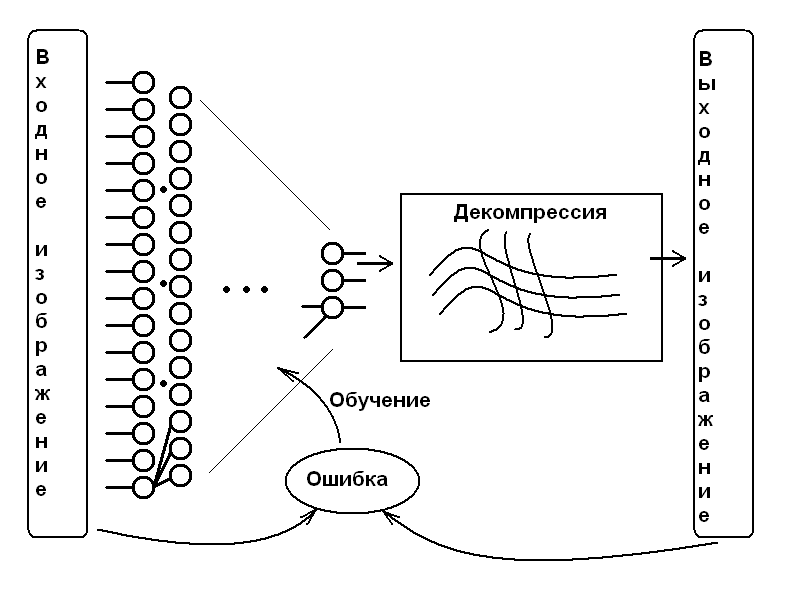
Нюанс первый. Алгоритм сжатия, пытающийся всё привести к фиксированному размеру — вещь условно-полезная, чтобы не сказать хуже. Реальный объём информации в изображении может различаться на порядки, от «красивые облака» до «страничка из рукописи Войнича» (да, в эксперменте не просто так самое сокрушительное фиаско потерпел даже не домик, который нейросеть заменила на совершенно другой домик, а надписи на рисунках). Для этого при обучении сети нужно добавить новый входной параметр: «требуемый размер», в который сеть должна уложиться. Выходные сигналы, подаваемые на «разжималку», просто обрезаются до номера N, а всё от него и выше — отбрасывается (тут возможны, однако, некоторые краевые эффекты, влияющие на адекватность последнего, N-1-го выходного сигнала). Разумно при этом итоговую ошибку, возникающую между восстановленным изображением и оригиналом, делить на N: это позволит не требовать от сети невозможного и не обучать её «слишком заостряться» на попытках спасения безнадёжно пережатых изображений в ущерб «выработке навыков» получения по-настоящему хорошего изображения там, где это было бы возможно. И, наверное, не менее разумно было бы при обучении использовать каждое изображение многократно с разными требованиями, обучая сеть сжимать его в разном качестве — от максимального до минимального.

Нюанс второй. Выбор алгоритма оценки — не самая элементарная задача. Что именно принять за итоговую ошибку, которую следует минимизировать? Какой должна быть штрафная функция при обучении? СКО, конечно, показательно в качестве «средней температуры по больнице», но всерьёз относиться к этому параметру явно не стоит. Максимальная ошибка? Слишком много внимания к одному пикселу шума.
Выбросоустойчивые оценки (иногда называемые поистине кошмарным словосочетанием «робастные эстиматоры»)?
Хорошо, допустим, мы нашли хороший критерий оценки шума. Но тут нас подстерегает ещё одна проблема: это деформации. Смещение однопиксельной линии на пол-пиксела, в общем, не является для изображения фатальным (будучи и так на грани разрешения, оно не очень информативно). С точки же зрения шума, изменение линии по всей длине аж на половину динамического диапазона в её изначальном месте и возникновение в новом — это не меньшая ошибка, чем полное отсутствие линии, и бо́льшая, чем изуродованная до состояния пунктира линия.


Во всяком случае, не вооружившись достаточно совершенной «смарт-оценкой», бросаться на задачу определённо нет смысла. С точки зрения шума, проще заменить «В» на «Б».
Нюанс третий. В выборе конкретной системы кодирования прячется довольно много «дьявола в деталях». Отложим такой напрашивающийся вариант, как фрактальные энкодеры (я не просто так их упоминаю, у них есть свой фандом, досконально знающий все подводные камни — что ж, сейчас их выход к роялю). Я же разберу на порядок более простой, но тем не менее уже мало поддающийся традиционным способам разложения, вариант: частотный анализ, ограниченный произвольными областями. Это что-то вроде кошмарного гибрида вейвлетов и векторизации изображения: надо разбить изображение на стопку слоёв-слагаемых, каждое из которых задано контуром (отметим его зелёным) и заполнено некоторым набором гармоник (отметим их красным). Кошмарного в том смысле, что наше зрение решает эту задачу мгновенно («вот одна ветка дерева, листья расположены так-то и так-то, вот вторая, вот рябь на воде, вот галька» — это всё именно что отдельные области изображения, которые можно обвести контуром), но решить эту задачу без нейросетей — математический кошмар, особенно с учётом того, что для максимальной эффективности области могут и должны частично накладываться).
Какой же отпечаток накладывает этот декодер на обучение в целом? Во-первых, необходимый объём информации для хранения одного контура зависит от сложности формы контура. Во-вторых — от количества гармоник. Например, «квадратно-гнездовую застройку» наиболее эффективно охватить одним сложным контуром, в котором сложные гармоники задают паттерн одинаковых зданий (идеальная «квадратно-гнездовая застройка» в природе не встречается, но для примера…) Это, конечно, будет большой объём информации — но он сразу покроет большую часть изображения. И для того, чтобы поощрить сеть создавать максимально эффективные контуры, мы даём ей значительный запас выходов, позволяющих задать много, например, кривых Безье (или как уж мы захотим задать контур) и гармоник. Затем, согласно требуемой степени сжатия, производим квантование выходов (как гармоник, так и контуров). Оцениваем требуемый объём информации для каждого.
Сортируем в порядке возрастания контрастности. И затем, вместо того, чтобы брать первые N контуров, как в «сферовакуумном» примере — выбираем контуры в порядке нарастания контрастности (т. е. влияния на изображение), пока не наберётся требуемый объём в количестве N (плюс-минус до ближайшего целого описания одного контура). И только уже полученные квантованные контуры, заполненные квантованными гармониками, подаём на «разжималку» и потом на «умную оценку ошибки», обучая нейросеть наилучшим образом использовать весьма запутанные и сложные закономерности между уровнями на выходах и объёмом информации, в который нужно «уложиться» (а заодно и обезопасив себя от краевых эффектов обучения для N-1-го выходного сигнала).

Как легко видеть, это сильно отличается от общего случая выше. Пространство выходных параметров жёстко разбито на области (максимальное количество которых должно покрывать самое высокое качество сжатия самого сложного изображения), где каждая область разбита на тем или иным способом закодированную форму контура (количество выделенных под это сигналов соответствует самому сложному контуру) и коэффициенты при гармониках (тоже соответствующие самому худшему случаю). Суммарное количество выходов наверняка окажется сравнимо с количеством входов, но поскольку случаи, где всё одновременно протекает по наихудшему сценарию, являются вырожденными либо вовсе принципиально невозможными — это не должно смущать, потому что после квантования, сортировки и отбрасывания наименее контрастных (предполагаю, что при этом лучше игнорировать размер области вовсе, чтобы важность мелких и крупных деталей определяла сама нейросеть) — количество «выживших» усохнет на пару порядков. И даже более того — если «кошмарный» кодек и не покажет высокую степень сжатия, любой работоспособный результат уже очень показателен в плане возможности нейросетей владеть самыми жуткими способами кодирования изображения.
Таким образом, если кто-то владеет вопросами «умной» оценки ошибок значительно лучше, чем я, и вдобавок может представить себе принципы, по которым можно описывать контуры доступным для нейросети образом (да ещё так, чтобы они поддавались квантованию с «огрублением» контура) — я желаю удачи этому отважному естествоиспытателю.
И если кого-то из тех, кто имел дело с фрактальным сжатием, эти соображения навели на аналогичные мысли в их епархии — уступаю им трибуну.
Критика приветствуется (кроме указания на то, что это всё — не более чем соревнования по акробатической имхонавтике на брусьях, потому что это обстоятельство уже известно и занесено в «known bugs», повторяться нет смысла). Особенно приветствуется оперативная критика, пока не поздно исправить ашыпки, очпеятки и некорректурное использование терминологии.
ссылка на оригинал статьи https://habr.com/ru/post/713790/
Добавить комментарий