
Рисунок 1. Модель логистической регрессии. Источник.
Логистическая регрессия использовалась в области биологических исследований ещё в начале двадцатого века. Затем её стали применять во многих общественных науках. Логистическая регрессия применима, когда зависимая переменная (целевое значение) является категориальной. Подробности в иллюстрациях — в материале, а практика — на нашем курсе, посвящённом Data Science.
Например, нам нужно предсказать:
- является ли электронное письмо спамом (1) или нет (0);
- является ли опухоль злокачественной (1) или доброкачественной (0).
Попробуем ответить на второй вопрос.
Сайшрути, судя по всему, допустила здесь ошибку при переработке своего текста, так как сначала написано «Consider a scenario where we need to classify whether an email is spam or not», а потом «Say if the actual class is malignant…the data point will be classified as not malignant which can lead to serious consequence in real time», поэтому, чтобы всё было последовательно и логично, первое предложение пришлось поменять. Второе менять нельзя, так как важность этих задач и последствия ошибки классификации несопоставимы. — прим. перев.
Если использовать для этого линейную регрессию, нужно сначала задать порог последующей классификации. Если опухоль действительно злокачественная, предсказанное непрерывное значение — 0,4, а пороговое значение — 0,5, то точка данных будет классифицирована как доброкачественная опухоль. Такое заключение может привести к катастрофе.
Этот пример показывает, что линейная регрессия не [всегда] подходит для решения задачи классификации. Линейная регрессия не имеет привязки, поэтому часто нужно пользоваться логистической регрессией, где значение строго варьируется от 0 до 1.
Простая логистическая регрессия
Модель
- На выходе модели значения 0 или 1.
- Гипотеза => Z = WX + B.
- hΘ(x) = sigmoid(Z).
Сигмоидная функция
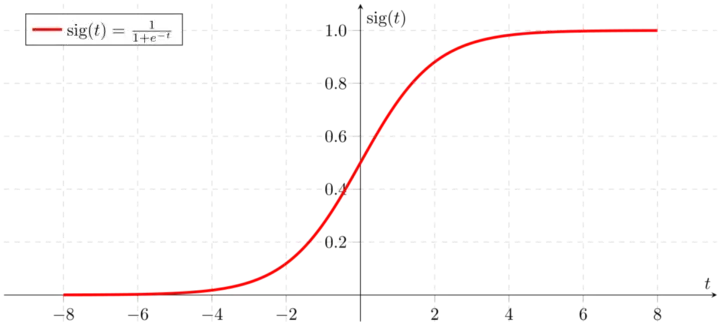
Рисунок 2. Сигмоидальная функция активации
Предполагаемое значение Y(predicted) стремится к 1 при положительно бесконечном Z, а к 0 — при отрицательно бесконечном Z.
Анализ гипотезы
С этой гипотезой на выходе получаем оценку вероятности. Она определяет уверенность в том, что оцениваемое значение совпадёт с фактическим. На входе — значения X0 и X1. На основании значения x1 мы можем оценить вероятность как 0.8. Таким образом, вероятность, что опухоль является злокачественной, равна 80%.
Записать можно так:

Рисунок 3. Математическое представление
Этим и обусловлено название — логистическая регрессия. Данные вписываются в модель линейной регрессии, на которую затем действует логистическая функция. Эта функция описывает целевую категориальную зависимую переменную.
Типы логистической регрессии
1. Бинарная логистическая регрессия.
Классификация всего по 2 возможным категориям, например на предмет спама.
2. Мультиномиальная логистическая регрессия.
Это три и более категорий без ранжирования, например, определение наиболее популярной системы питания (вегетарианство, невегетарианство, веганство).
3. Ординальная логистическая регрессия
Ранжирование по трём и более категориям — рейтинг фильмов с оценками от 1 до 5
Граница решений (Decision Boundary)
Чтобы определить, к какому классу относятся данные, устанавливается пороговое значение. На основе этого порога полученная оценка вероятности классифицируется по классам.
Например, если предсказанное_значение ≥ 0,5, то письмо классифицируется как «спам», в противном случае — как «не спам».
Граница принятия решения может быть линейной или нелинейной. Порядок полинома можно увеличить, чтобы получить сложную границу решений.
Функция потерь (функция стоимости)

Рисунок 4. Функция потерь логистической регрессии
Почему функция потерь, которая использовалась для линейной регрессии, неприменима для логистической регрессии? В линейной регрессии в качестве функции стоимости используется среднеквадратичная ошибка. Если использовать её для логистической регрессии, то функция параметров (tetha) будет невыпуклой, а градиентный спуск сходится к глобальному минимуму, только в случае выпуклой функции.

Рисунок 5. Выпуклая и невыпуклая функции потерь
Объяснение функции потерь

Рисунок 6. Функция потерь: часть 1

Рисунок 7. Функция потерь: часть 2
Упрощённая функция потерь

Рисунок 8. Упрощённая функция потерь
Почему функция потерь выглядит так?

Рисунок 9. Объяснение метода максимального правдоподобия: часть 1

Рисунок 10. Объяснение метода максимального правдоподобия: часть 2
Эта функция отрицательная, поскольку при обучении нужно максимизировать вероятность, минимизируя функцию потерь. Снижение потерь приведет к увеличению максимального правдоподобия при допущении, что выборки взяты из идентичного независимого распределения.
Вывод формулы для алгоритма градиентного спуска

Рисунок 11. Алгоритм градиентного спуска: часть 1

Рисунок 12. Объяснение алгоритма градиентного спуска: часть 2
Реализация на Python:
def weightInitialization(n_features): w = np.zeros((1,n_features)) b = 0 return w,b def sigmoid_activation(result): final_result = 1/(1+np.exp(-result)) return final_result def model_optimize(w, b, X, Y): m = X.shape[0] #Prediction final_result = sigmoid_activation(np.dot(w,X.T)+b) Y_T = Y.T cost = (-1/m)*(np.sum((Y_T*np.log(final_result)) + ((1-Y_T)*(np.log(1-final_result))))) # #Gradient calculation dw = (1/m)*(np.dot(X.T, (final_result-Y.T).T)) db = (1/m)*(np.sum(final_result-Y.T)) grads = {"dw": dw, "db": db} return grads, cost def model_predict(w, b, X, Y, learning_rate, no_iterations): costs = [] for i in range(no_iterations): # grads, cost = model_optimize(w,b,X,Y) # dw = grads["dw"] db = grads["db"] #weight update w = w - (learning_rate * (dw.T)) b = b - (learning_rate * db) # if (i % 100 == 0): costs.append(cost) #print("Cost after %i iteration is %f" %(i, cost)) #final parameters coeff = {"w": w, "b": b} gradient = {"dw": dw, "db": db} return coeff, gradient, costs def predict(final_pred, m): y_pred = np.zeros((1,m)) for i in range(final_pred.shape[1]): if final_pred[0][i] > 0.5: y_pred[0][i] = 1 return y_pred
Потери и число итераций

Рисунок 13. Снижение стоимости
Точность обучения и тестирования системы — 100%. Эта реализация относится к бинарной логистической регрессии. При использовании более 2 классов нужно использовать регрессию Softmax.
Этот обучающий материал создан на основе курса по глубокому обучению профессора Эндрю Ына.
Вот весь код.
Data Science и Machine Learning
- Профессия Data Scientist
- Профессия Data Analyst
- Курс «Математика для Data Science»
- Курс «Математика и Machine Learning для Data Science»
- Курс по Data Engineering
- Курс «Machine Learning и Deep Learning»
- Курс по Machine Learning
Python, веб-разработка
- Профессия Fullstack-разработчик на Python
- Курс «Python для веб-разработки»
- Профессия Frontend-разработчик
- Профессия Веб-разработчик
Мобильная разработка
Java и C#
- Профессия Java-разработчик
- Профессия QA-инженер на JAVA
- Профессия C#-разработчик
- Профессия Разработчик игр на Unity
От основ — в глубину
А также
ссылка на оригинал статьи https://habr.com/ru/company/skillfactory/blog/714244/

Добавить комментарий