Книга «Основы Python для Data Science»

Python — язык программирования №1 для машинного обучения и Data Science. Но как же сложно решить, с чего начать изучение Python, ведь у него огромный инструментарий! Кеннеди Берман фокусируется на тех навыках программирования, которые понадобятся вам для решения задач в области Data Science и машинного обучения.

Вы познакомитесь с блокнотами Jupyter — лучшей средой для профессиональной работы с данными. Затем перейдете к ключевым библиотекам, которые упрощают процесс математических вычислений, визуализации, решение задач машинного обучения и обработки естественного языка. Затем, овладев основами, вы перейдете к продвинутым техникам, позволяющим решать более сложные задачи.

Библиотека SciPy

Многие используют статистику так же,
как пьяный — фонарные столбы:
для поддержки, а не для освещения.

Эндрю Лэнг

Обзор SciPy

Библиотека SciPy — это набор основанных на NumPy пакетов, предоставляющих инструменты для научных расчетов через компьютер. Она включает подмодули, которые занимаются оптимизацией, преобразованиями Фурье, обработкой сигналов и изображений, линейной алгеброй и, среди прочего, статистикой. Эта глава затрагивает три подмодуля: scipy.misc, scipy.special и scipy.stats — наиболее полезный для Data Science.

В некоторых примерах главы используется библиотека matplotlib. Она позволяет визуализировать разные типы графиков, диаграмм и изображений. По соглашению для импорта библиотеки построения графиков ее нужно импортировать с именем plt:

import matplotlib.pyplot as plt

Подмодуль scipy.misc

Подмодуль scipy.misc содержит функции, которым больше нигде нет места. Одна из забавных функций этого модуля — scipy.misc.face(), которая может быть запущена с помощью следующего кода:

from scipy import misc import matplotlib.pyplot as plt face = misc.face() plt.imshow(face) plt.show()

Вы можете попробовать это самостоятельно, чтобы сгенерировать вывод.

Функция ascent возвращает изображение в градациях серого, доступное для использования и демонстрации. При вызове ascent() результатом будет двумерный массив NumPy:

a = misc.ascent() print(a) [[ 83 83 83 ... 117 117 117] [ 82 82 83 ... 117 117 117] [ 80 81 83 ... 117 117 117] ... [178 178 178 ... 57 59 57] [178 178 178 ... 56 57 57] [178 178 178 ... 57 57 58]]

Если вы передадите этот массив объекту графика matplotlib, то увидите изображение, как на рис. 8.1:

plt.imshow(a) plt.show()

Здесь видно, что метод plt.imshow() используется для визуализации изображений.

Подмодуль scipy.special

Подмодуль scipy.special содержит утилиты для математической физики: функции Эйри, эллиптические функции, функции Бесселя, Струве и многие другие. Большинство из них поддерживают бродкастинг и совместимы с массивами NumPy. Чтобы использовать эти функции, просто импортируйте scipy.special из SciPy и вызовите их напрямую. Например, с помощью функции special.factorial() можно вычислить факториал числа:

from scipy import special special.factorial(3) 6.0

Рассчитать количество сочетаний и перестановок можно так:

special.comb(10, 2) 45.0 special.perm(10,2) 90.0

ПРИМЕЧАНИЕ
У scipy.special есть некоторые низкоуровневые функции из подмодуля scipy.stats, но они не предназначены для прямого использования. scipy.stats применяется в статистических целях. Вы познакомитесь с ним в следующем разделе.

Подмодуль scipy.stats

scipy.stats предлагает распределение вероятностей и статистические функции. Ниже рассматриваются несколько распределений, предлагаемых этим подмодулем.

Дискретные распределения

SciPy предлагает несколько дискретных распределений, применяющих общие методы. Они показаны в листинге 8.1, где используется биномиальное распределение — некоторое количество проб, результат каждой из которых либо успешен, либо неудачен.

Листинг 8.1. Биномиальное распределение

from scipy import stats B = stats.binom(20, 0.3) # Определение биномиального распределения,                          # состоящего из 20 испытаний и 30 % шансов на успех  B.pmf(2) # Вероятностная функция (вероятность того, что выборка равна 2) 0.02784587252426866  B.cdf(4) # Кумулятивная функция распределения (вероятность того, что          # выборка меньше 4) 0.2375077788776017  B.mean # Среднее значение распределения 6.0  B.var() # Дисперсия распределения 4.199999999999999  B.std() # Стандартное отклонение распределения 2.0493901531919194  B.rvs() # Получение случайной выборки из распределения 5  B.rvs(15) # Получите 15 случайных выборок array([ 2, 8, 6, 3, 5, 5, 10, 7, 5, 10, 5, 5, 5, 2, 6])

Если вы возьмете достаточно большую случайную выборку распределения

rvs = B.rvs(size=100000) rvs array([11, 4, 4, ..., 7, 6, 8])

то можете использовать matplotlib для построения графика и получения представления о его форме (см. рис. 8.2):

import matplotlib.pyplot as plt plt.hist(rvs) plt.show()

Числа в нижней части распределения на рис. 8.2 — это количество успешных операций в 20-пробном эксперименте. Вы можете видеть, что 6 из 20 — наиболее распространенный результат, соответствующий 30 % вероятности успеха.

Другое распределение в подмодуле scipy.stats — распределение Пуассона. Оно моделирует вероятность определенного числа отдельных событий за некоторый промежуток времени. Форма распределения управляется его средним значением, которое вы можете установить с помощью ключевого слова mu. Например, более низкое значение, такое как 3, сдвинет распределение влево (рис. 8.3):

P = stats.poisson(mu=3) rvs = P.rvs(size=10000) rvs array([4, 4, 2, ..., 1, 0, 2]) plt.hist(rvs) plt.show()

Более высокое среднее значение, такое как 15, передвинет распределение вправо (см. рис. 8.4):

P = stats.poisson(mu=15) rvs = P.rvs(size=100000) plt.hist(rvs) plt.show()

Другие дискретные распределения в подмодуле scipy.stats: бета-биномиальное распределение, распределение Больцмана (усеченное Планка), распределение Планка (дискретный экспоненциал), геометрическое, гипергеометрическое, логарифмическое и распределение Юла-Саймона. На момент написания этой книги есть всего 14 распределений, моделируемых в подмодуле scipy.stats.

Непрерывные распределения

Подмодуль scipy.stats включает гораздо больше непрерывных распределений, чем дискретных. На момент написания книги их было 87. Все эти распределения принимают аргументы для местоположения (loc) и масштаба (scale). Все по умолчанию имеют местоположение 0 и масштаб 1.0.

К непрерывным распределениям относится нормальное, которое вы можете знать как колокол, или гауссову кривую. В этом симметричном распределении одна половина данных находится слева от среднего значения, а другая — справа.

Вот так можно создать нормальное распределение с помощью местоположения и масштаба по умолчанию:

N = stats. norm() rvs = N.rvs(size=100000) plt.hist(rvs, bins=1000) plt.show()

На рис. 8.5 показан график этого распределения.

Вы можете видеть, что распределение сосредоточено на 0 и находится примерно между –4 и 4. Рисунок 8.6 показывает результат создания второго нормального распределения — на этот раз установлено значение местоположения 30 и масштаб 50:

N = stats. norm() rvs = N.rvs(size=100000) plt.hist(rvs, bins=1000) plt.show()

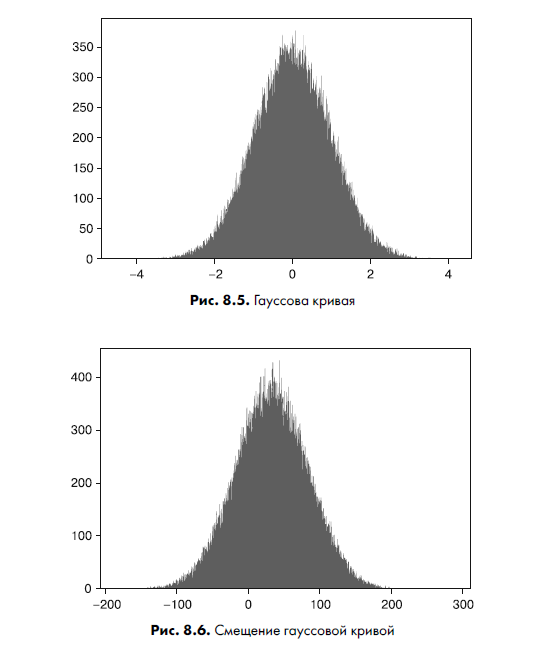
Обратите внимание, что распределение теперь сосредоточено вокруг 30 и охватывает куда более широкий диапазон чисел. У непрерывных распределений есть несколько общих функций, которые смоделированы в листинге 8.2. Заметьте, что здесь использовано второе нормальное распределение со смещенным местоположением и большим стандартным отклонением.

Листинг 8.2. Нормальное распределение

N1 = stats.norm(loc=30, scale=50) N1.mean() # Среднее значение распределения, которое соответствует значению loc 30.0  N1.pdf(4) # Функция плотности вероятности 0.006969850255179491  N1.cdf(2) # Кумулятивная функция распределения 0.28773971884902705  N1.rvs() # Случайная выборка 171.55168607574785  N1.var() # Дисперсия 2500.0  N1.median() # Медиана 30.0  N1.std() # Стандартное отклонение 50.0

ПРИМЕЧАНИЕ
Если вы попробуете воспроизвести показанные здесь примеры, некоторые из ваших значений могут отличаться из-за генерации случайных чисел.

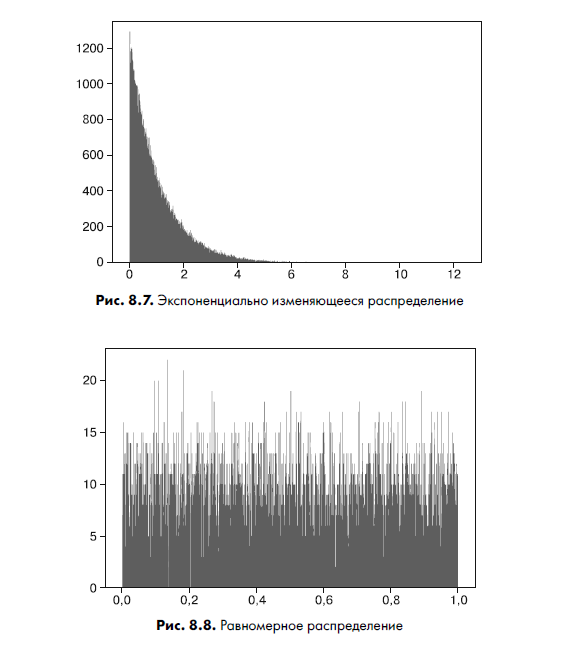
Следующее — экспоненциально изменяющееся непрерывное распределение — характеризуется экспоненциально изменяющейся кривой — либо вверх, либо вниз (рис. 8.7):

E = stats.expon() rvs = E.rvs(size=100000) plt.hist(rvs, bins=1000) plt.show()

Рисунок 8.7 отображает кривую, которую и следовало ожидать от экспоненциальной функции. Ниже приведено равномерное распределение с постоянной вероятностью, известное как прямоугольное распределение:

U = stats.uniform() rvs = U.rvs(size=10000) rvs  array([8.24645026e-01, 5.02358065e-01, 4.95390940e-01, ...,           8.63031657e-01, 1.05270200e-04, 1.03627699e-01])  plt.hist(rvs, bins=1000) plt.show()

Оно дает равномерно распределенную вероятность в заданном диапазоне, график которой показан на рис. 8.8.

Резюме

Обе библиотеки, NumPy и SciPy, предлагают утилиты для решения сложных математических задач. Они охватывают множество ресурсов, а их применению посвящены целые книги. Вы познакомились лишь с некоторыми из множества их возможностей. Эти библиотеки — первое, на что вам стоит обратить внимание, когда вы приступаете к решению или моделированию сложных математических задач.

Вопросы для закрепления

1. Используйте подмодуль scipy.stats для моделирования нормального распределения со средним значением 15.
2. Сгенерируйте 25 случайных выборок из распределения, смоделированного в вопросе 1.
3. У какого подмодуля SciPy есть утилиты, разработанные для математической физики?
4. Какой метод предоставляется дискретным распределением для вычисления его стандартного отклонения?

Более подробно с книгой можно ознакомиться на сайте издательства:
» Оглавление
» Отрывок

По факту оплаты бумажной версии книги на e-mail высылается электронная книга.
Для Хаброжителей скидка 25% по купону — Python