Введение в математическую оптимизацию на примере компании Recruit. Часть 4

Это серия статей о том, что такое математическая оптимизация и как её можно применить в бизнесе на примере компании Recruit. В данной статье мы рассказываем, как была решена проблема планирования доставки бесплатной газеты. Другие части доступны здесь:

❖ авторы Кенго Хамада, Котаро Танахаси

Примеры, представленные в предыдущих частях этой серии статей, были решены с помощью математического оптимизационного решателя общего назначения, но не все задачи могут быть эффективно решены таким образом. В данном примере сложность заключается в том, что решаемая проблема относится к типу, с которым не справляются математические решатели общего назначения. Мы надеемся, что подход, представленный в этой статье, поможет читателям решить подобные проблемы, если они с ними столкнутся.

Введение

Recruit размещает несколько бесплатных газет, в том числе Town Work и Hot Pepper Beauty, на стойках, вокзалах и в магазинах по всей Японии. Доставка бесплатных газет к каждому стеллажу осуществляется несколькими компаниями.

Поскольку компании по доставке грузов объезжают множество пунктов распространения газет на нескольких грузовиках, повышение эффективности маршрутов доставки является важным вопросом. Традиционно маршруты доставки грузов определялись вручную, но математическая оптимизация позволяет предложить более эффективные варианты.

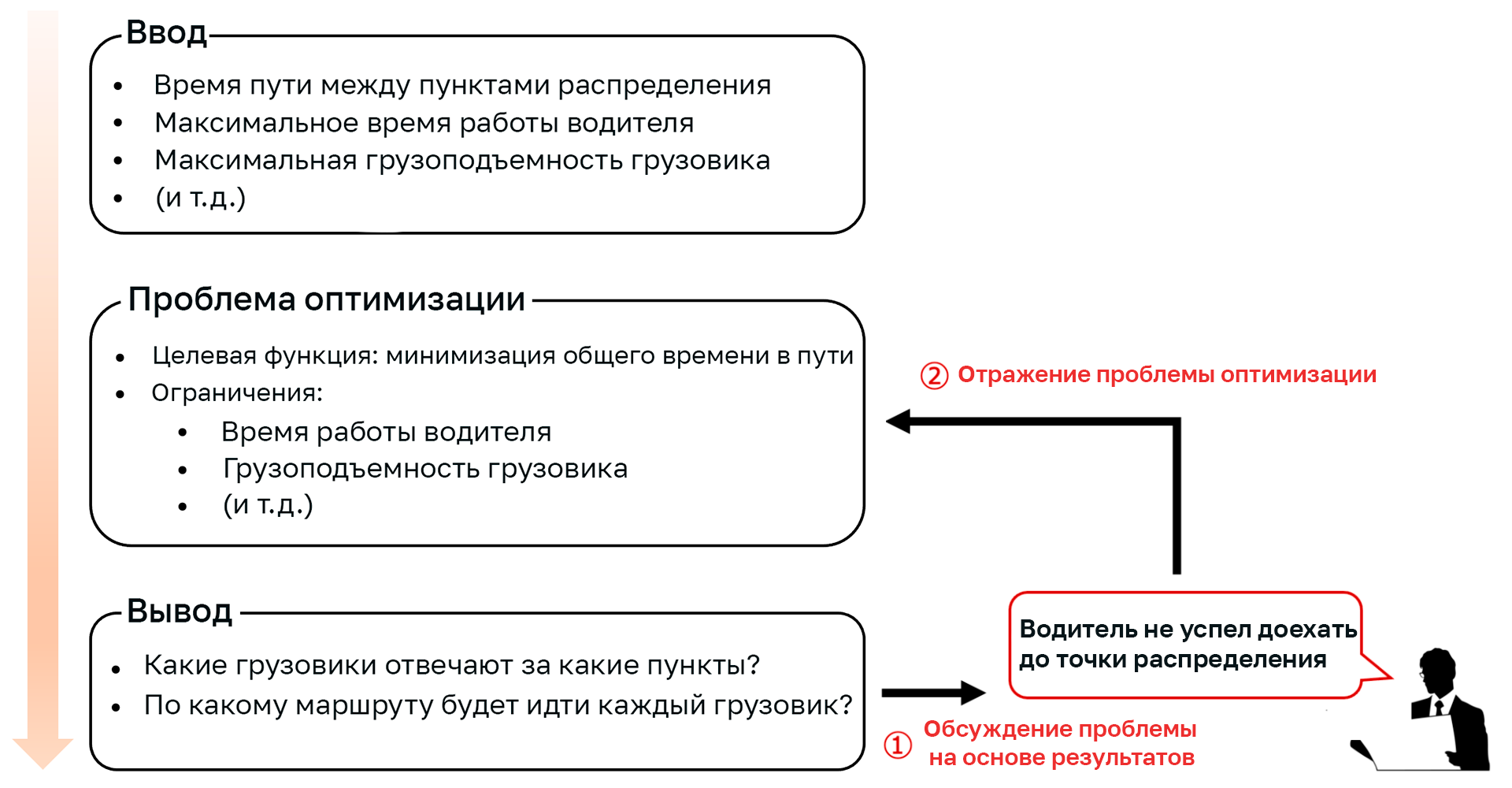
Понимание бизнес-проблемы

Грузовики отправляются со склада компании-доставщика, посещают пункты распределения и возвращаются обратно на склад. В данном случае на каждую точку должен заезжать один из грузовиков.

На схеме ниже показан маршрут доставки.

Есть две вещи, которые необходимо решить.

Какие грузовики будут отвечать за какие пункты распределения.
По какому маршруту каждый грузовик будет ехать.

Маршрут должен быть максимально эффективным, т. е. общее время в пути должно быть коротким. Обратите внимание, что время в пути между точками распределения должно быть указано в качестве входных данных.

Кроме того, необходимо соблюдать ряд практических ограничений, включая следующие пункты:

Время работы водителя.
Грузоподъёмность грузового автомобиля.
Время, необходимое для того, чтобы добраться до магазина.

Описанную до сих пор постановку задачи можно обобщить в виде следующего рисунка.

Несложно представить, как трудно людям думать о подобных вопросах. Однако верно и то, что существуют детальные требования, которые можно отрегулировать только вручную. Суть этого проекта заключается в том, насколько практичные решения мы можем предложить, чтобы их могли использовать в работе.

Подход математической оптимизации

Как уже упоминалось во второй статье данного цикла, обращение к типичной проблеме является полезным подходом при рассмотрении проблемы оптимизации. Для решения текущей задачи можно использовать задачу планирования доставки¹. Здесь был использован подход, заключающийся в том, чтобы начать с постановки базовой задачи для проблемы планирования доставки, а затем путём проведения опросов адаптировать её к оптимизационной задаче, более подходящей для данной проблемы.

1. Возможно, вы слышали о задаче коммивояжёра, поскольку это одна из самых известных оптимизационных проблем. Задача планирования доставки может рассматриваться как расширение задачи о странствующем торговце.

Проблема планирования доставки, с которой мы будем иметь дело, относится к тому типу проблем, которые плохо поддаются решению. Поэтому в данном проекте мы решили разработать собственный решатель специально для этой задачи, вместо того чтобы использовать решатель общего назначения.

В следующих разделах описывается процесс настройки оптимизационной задачи с помощью опросов, а затем разработка специального решателя.

▍ Обособление оптимизационной задачи с помощью опросов

Проблема планирования доставки давно изучена, и были предложены различные расширения, но основная постановка задачи выглядит следующим образом.

Построение задачи

Транспортное средство отправляется со склада, проходит через несколько пунктов распределения и снова возвращается на склад.
Местонахождение пунктов известно, и каждую точку может посетить только один из грузовых автомобилей и только один раз.
Время в пути между населёнными пунктами известно.
Количество используемых транспортных средств оговаривается заранее.

Целевая функция: минимизация общего времени в пути транспортных средств для перевозки грузов.

Ограничения

Не превышать установленное количество транспортных средств для перевозки грузов.
Все транспортные средства отправляются со склада и возвращаются на склад.
Все пункты распределения посещает ровно один автомобиль.
Учитывать предел грузоподъёмности транспортных средств для перевозки грузов.

Результат: оптимальный маршрут для каждого транспортного средства².

2. Рисунок, размещённый в разделе «Понимание бизнес-проблемы», показывает тот самый результат.

Этот процесс добавляет ряд практических ограничений к базовой схеме, описанной выше, и нацелен на расчёт маршрутов, действующих на практике.

Конкретные ограничения будут определены в ходе опросов, но трудно получить всю необходимую информацию, просто спросив, например, «Что добавить?».

Одно из возможных решений — обсуждение проблемы на основе результатов. Например: «Взгляните на эти результаты и скажите нам, что из этого нереализуемо на практике». В данном проекте мы добавили по одному ограничению за раз, чтобы решить эти моменты, которые на практике неприменимы.

▍ Разработка специального решателя

Основные направления подхода к решению оптимизационных задач можно организовать следующим образом (ссылка: материал профессора Шундзи Уметани на японском языке).

Общий метод решения: формулировать и применять общий решатель для решения, например, задачи целочисленного программирования.

Специальный метод решения: разработка специального решателя, использующего особенности отдельных проблем.

Преимуществом методов решения общего назначения является простота разработки, поскольку можно использовать такие решатели, как Gurobi и CBC, но многие оптимизационные задачи решить сложно. С другой стороны, специальные методы решения требуют больше времени и усилий, поскольку их нужно разрабатывать индивидуально, но можно быть уверенным, что они обеспечат высокую производительность.

Как упоминалось в начале этого раздела, задачи планирования доставки трудно решить с помощью общих методов решения, поэтому здесь был разработан специальный решатель.

На этот раз проблема заключается в том, что нужно найти эффективный маршрут. Как мы можем этого достичь?

Во-первых, запишем маршрут соответствующим образом. Обратите внимание, что для простоты здесь мы рассматриваем только один круговой маршрут.

Стрелки, обозначающие маршруты, перепутаны и выглядят очень неэффективно. Давайте улучшим решение. Трудно сделать более эффективными сразу все маршруты, поэтому мы сосредоточимся только на двух стрелках и изменим их. Например, если заменить две стрелки красного цвета, как на рисунке ниже, маршрут выглядит немного более эффективным.

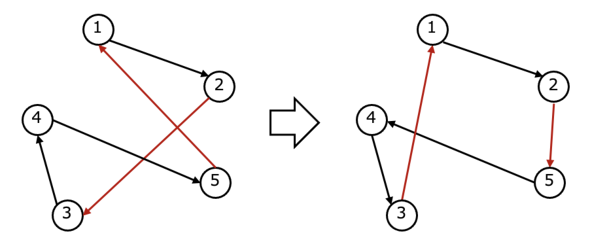
Давайте продолжим немного дальше. Теперь попробуем поменять местами ещё две стрелки, показанные красным цветом. Тогда стрелки больше не пересекаются, и мы получаем маршрут, который кажется более эффективным.

Этот метод накопления локальных улучшений называется методом локального поиска. В частности, описанный выше алгоритм называется 2-opt и часто используется в задачах оптимизации маршрутов.

Ещё один подход, который успешно использует методы локального поиска в качестве компонентов для более продвинутой оптимизации, — метаэвристика. Для данной задачи был разработан специальный решатель, использующий метод отжига.

Последствия внедрения

В результате могут быть найдены более эффективные маршруты, чем обычные, что открывает перспективу доставки меньшим количеством транспортных средств.

Как компания, занимающаяся доставкой, вы можете рассчитывать на решение проблемы нехватки водителей за счёт повышения эффективности работы.

Заключение

Использование математической оптимизации варьируется от случая к случаю, поэтому мы надеемся, что демонстрация нескольких примеров её применения поможет лучше понять общую картину.

На данной статье мы завершаем цикл о введении в математическую оптимизацию. Последней частью является стенограмма в виде беседы с профессором Шундзи Уметани и мы думаем, что для Хабра подобный формат интереса не представляет. Было приятно и интересно переводить для вас статьи с японского языка. Надеемся, что эксперимент был удачный.

Вы можете написать в комментариях, на какую тему вы бы хотели почитать материал, или же какие-то конкретные статьи для перевода. Если повезёт, то встретимся с вами вновь.

Telegram-канал с розыгрышами призов, новостями IT и постами о ретроиграх

ссылка на оригинал статьи https://habr.com/ru/company/ruvds/blog/706680/