
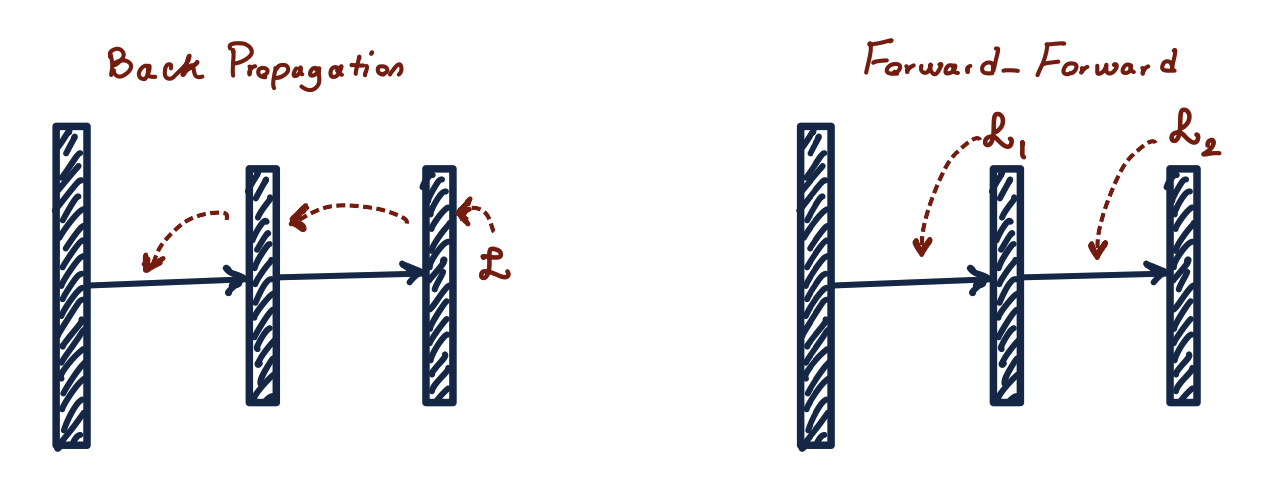
Алгоритм обратного распространения ошибки уже давно доминирует в сфере обучения нейронных сетей. Несмотря на свою популярность и эффективность, у него есть свои недостатки, в частности, различие в работе с человеческим мозгом.
В конце прошлого года Джеффри Хинтон, пионер Deep Learning, на конференции NeurIPS 2022 предложил новый алгоритм обучения нейронных сетей — Forward‑Forward — как альтернативу методу обратного распространения ошибки. FF более гибок и использует меньше памяти, чем backpropagation в архитектурах с множеством скрытых слоев, а его основная отличительная черта в том, что он основывается на современном понимании устройства человеческого мозга.
В данной статье мы рассмотрим: что способствовало появлению данного алгоритма, принцип его работы, а также обучим с его помощью простейшую классифицирующую нейросеть на датасете — MNIST.
Истоки
Алгоритм backpropagation имеет ряд ограничений: необходимость сохранять активации на каждом слое, а также граф вычислений, без которого расчет правильной производной невозможен. Кроме того, на время вычисления производной необходимо делать остановку, то есть перестать принимать поступающие данные. Человек способен производить инференс и обучение в реальном времени без остановки на расчет ошибки. Исследователи склоняются к тому, что мозг не может учиться с помощью алгоритма backpropagation. А Джеффри Хинтон хочет сделать все как в мозге. Хинтон полагает, что алгоритм обратного распространения ошибки плохо мимикрирует процессы, проходящие в мозге человека во время обучения. Его известная цитата об этом алгоритме: «Я считаю, что нужно выбросить все и начать сначала. Будущее зависит от выпускника, который глубоко сомневается во всем, что я говорю». Не дождавшись выпускника, Джеффри сам предлагает новый подход к обучению.
Принцип работы
Алгоритм является процедурой обучения многослойных нейросетей, вдохновленный принципом работы машины Больцмана. Идея заключается в замене стандартной комбинации прямого прохода и обратного распространения ошибки на два прямых прохода, которые отличаются только данными и противоположными целевыми функциями. Положительный проход производится на реальных данных и настраивает веса для увеличения добротности (goodness) в каждом скрытом слое. Негативный проход использует искусственные данные для уменьшения добротности в каждом слое. Измерять добротность можно по‑разному: как сумму активаций в квадрате или негативную сумму активаций в квадрате.
Представим, что функция добротности для слоя — это сумма квадратов ReLU активаций в этом слое. Цель обучения — сделать добротность гораздо выше некоторого порога для реальных данных и ниже — для искусственных.
Есть нюанс в обучении каждого слоя по отдельности. При передаче активаций из первого во второй слой определение добротности из первого слоя для второго становится тривиальной задачей, так как он может ориентироваться на длину вектора. Нет необходимости обучаться новым фичам. Для решения этой проблемы в каждый слой была введена нормализация. Таким образом, длина вектора используется в текущем слое для определения добротности, а в следующем слое после нормализации остается только направление этого вектора.

Обучение без учителя
Для построения векторов, представляющих изображения, нам не обязательно иметь разметку, достаточно иметь искусственные данные. Таким образом, мы можем получить сеть, которая кластеризует похожие и разделяет разные изображения в векторном пространстве. В дальнейшем можно использовать обученные скрытые слои для решения различных задач: например, обучения линейного слоя с softmax для классификации изображений. Искусственные данные можно получить многими путями — в статье рассматривается размытие реальных изображений.
Эксперименты с таким подходом оказались удачными и показали ошибку 1,37% в нейросети с линейными слоями и 1,16% — cо сверточными.
Обучение с учителем
Теперь перейдем к примеру с обучением сети для классификации с использованием алгоритма FF на PyTorch. Ноутбук доступен в репозитории.
Для начала импортируем все необходимые библиотеки и определим — на каком устройстве мы будем проводить вычисления:
import torch import torch.nn as nn from tqdm import tqdm from torch.optim import Adam from torchvision.datasets import MNIST from torchvision.transforms import Compose, ToTensor, Normalize, Lambda from torch.utils.data import DataLoader import numpy as np DEVICE = 'cuda' # DEVICE = 'cpu'Из‑за специфики используемой нами функции потерь, мы не можем просто передать лейбл как отдельное число, так как его необходимо закодировать во входных данных. Для этого создадим функцию, кодирующую лейбл в первых (слева сверху) пикселях изображения. Так как у нас всего 10 классов, нам нужно выделить для этого 10 пикселей. Сами лейблы предстанут в виде one‑hot векторов.
def overlay_y_on_x(x, y): x_ = x.clone() x_[:, :10] *= 0.0 x_[range(x.shape[0]), y] = x.max() return x_Также нам понадобится функция для создания негативных данных, в качестве которых будут поданы те же самые изображения, только с неправильными лейблами. Таким образом, разница между позитивными и негативными экземплярами состоит только в лейбле и сеть будет игнорировать признаки, которые с ним не коррелируют. В «теле» функции убираем класс, к которому действительно принадлежит картинка, из списка всех возможных классов. Таким образом, мы не сможем случайно получить изображение с правильным классом.
def generate_negative_data(x, y): y_neg = y.clone() for idx, y_samp in enumerate(y): allowed_indices = [i for i in range(10)] allowed_indices.pop(y_samp.item()) y_neg[idx] = torch.tensor(np.random.choice(allowed_indices)).to(DEVICE) return overlay_y_on_x(x, y_neg)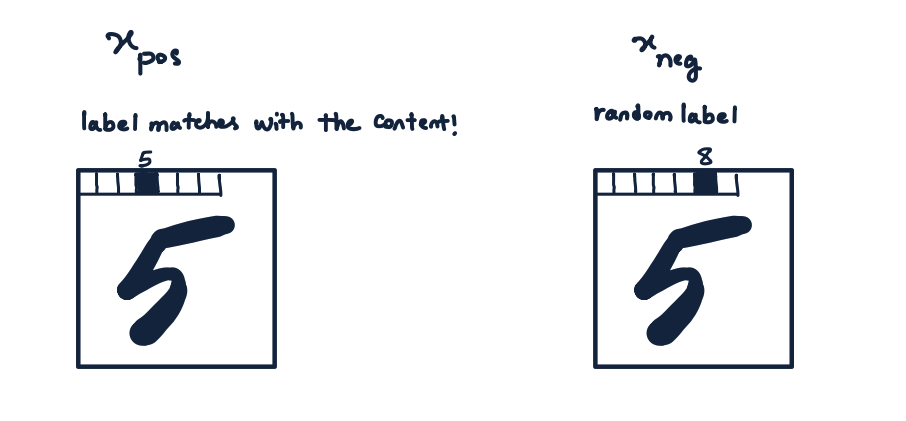
Перейдем к определению слоя сети. За основу берем линейный слой, в конструкторе задаем функцию активации ReLU и оптимизатор. Здесь же мы определяем новый гиперпараметр — порог разделения реальных и искусственных данных. Этот порог выбирается эмпирическим путем. Необходимо указывать количество эпох, так как каждый слой обучается отдельно.
В методе forward мы прежде всего избавляемся от длины вектора, вычисляя ее по каждому экземпляру в батче и меняем shape, чтобы без труда провести деление входных векторов. Данная реализация нормализации соответствует описанной в статье: среднее значение не вычитается перед делением из исходных векторов. Во избежание деления на ноль при нулевой длине вектора прибавляем к делителю небольшой эпсилон 1e-4. Далее все как в обычном линейном слое — перемножаем нормализованный x на веса, прибавляем байес и прогоняем через функцию активации.
Вот мы подошли к методу train. Напоминаю, что все слои учатся по отдельности: в начале вычисляем функцию добротности для положительных и отрицательных данных. В нашем случае она очень простая — значения pos_loss и neg_loss нужно минимизировать. Потом соединяем полученные тензоры и применяем к ним трюк log exp для предотвращения затухания или взрыва градиента, после чего берем среднее значение. Считаем производную методом backward (в данном случае он считает только производную на одном слое и не распространяет ошибку по графу) и делаем шаг оптимизатора. Возвращаем вывод слоя, предварительно отвязав его от графа вычислений. Вывод понадобится нам для подачи в следующий слой.
class Layer(nn.Linear): def __init__(self, in_features, out_features, bias=True, device=None, dtype=None): super().__init__(in_features, out_features, bias, device, dtype) self.relu = torch.nn.ReLU() self.opt = Adam(self.parameters(), lr=0.03) self.threshold = 3.0 self.num_epochs = 1000 def forward(self, x): x_direction = x / (x.pow(2).sum(dim=1).sqrt().reshape((x.shape[0], 1)) + 1e-4) return self.relu( torch.mm(x_direction, self.weight.T) + self.bias.unsqueeze(0)) def train(self, x_pos, x_neg): for i in range(self.num_epochs): g_pos = self.forward(x_pos).pow(2).mean(1) g_neg = self.forward(x_neg).pow(2).mean(1) pos_loss = -g_pos + self.threshold neg_loss = g_neg - self.threshold loss = torch.log(1 + torch.exp(torch.cat([ pos_loss, neg_loss]))).mean() self.opt.zero_grad() loss.backward() self.opt.step() return self.forward(x_pos).detach(), self.forward(x_neg).detach()Теперь определим саму модель. Метод train очень прост — по очереди обучаем слои и передаем результат в следующий слой. Необычный метод используется при инференсе — нужно посчитать метрику добротности для каждой комбинации входных данных и возможных классов, после чего возвращается класс с наибольшей добротностью. Можно использовать и softmax, но в таком случае результаты классификации будут менее точными.
class Net(torch.nn.Module): def __init__(self, dims): super().__init__() self.layers = [] for d in range(len(dims) - 1): self.layers += [Layer(dims[d], dims[d + 1]).to(DEVICE)] def predict(self, x): goodness_per_label = [] for label in range(10): h = overlay_y_on_x(x, label) goodness = [] for layer in self.layers: h = layer(h) goodness += [h.pow(2).mean(1)] goodness_per_label += [sum(goodness).unsqueeze(1)] goodness_per_label = torch.cat(goodness_per_label, 1) return goodness_per_label.argmax(1) def train(self, x_pos, x_neg): h_pos, h_neg = x_pos, x_neg for i, layer in enumerate(self.layers): h_pos, h_neg = layer.train(h_pos, h_neg)И, наконец, мы можем приступить к обучению. Загружаем датасет, создаем трехслойную сеть и запускаем обучение. Для формирования входных данных используем ранее заданные функции.
torch.manual_seed(1234) train_loader, test_loader = MNIST_loaders() net = Net([784, 512, 512]) for x, y in tqdm(train_loader): x, y = x.to(DEVICE), y.to(DEVICE) x_pos = overlay_y_on_x(x, y) x_neg = generate_negative_data(x, y) net.train(x_pos, x_neg)С данной конфигураций ошибка на тренировочных данных составила 2,04%, на тестовых — 4,74%. Нейросеть, обученная в статье, показала ошибку 0,64%. Однако, автор обучал сеть с 4 скрытыми слоями по 2000 нейронов в каждом на аугментированных данных. Кроме того, при подсчете метрики добротности он не использовал первый скрытый слой. Такой сетап только ухудшал мои показатели, и ошибка была на уровне 11%, так что результаты статьи воспроизвести не удалось. Обучение с аугментацией протестировано не было. Предлагаю вам поэкспериментировать с кодом и посмотреть что получится.
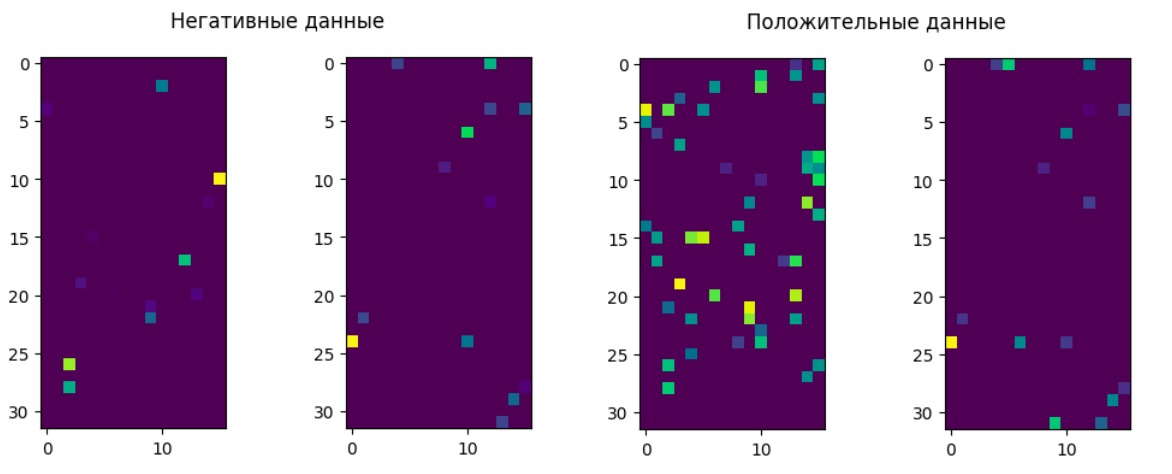
Мы можем визуализировать активации в скрытых слоях и увидеть, что на положительных данных активность «нейронов» выше, чем на отрицательных. В данном случае мы подавали в сеть картинку цифры семь с лейблами 0 и 7.
Джеффри в своей статье также провел эксперимент на датасете CIFAR-10. При использовании backpropagation ошибка уменьшалась значительно быстрее и с FF точность была немного ниже.
FF как альтернатива GAN
GAN (генеративная состязательная сеть) использует многослойную сеть для генерации данных и обучает свою генеративную модель с помощью многослойной дискриминативной сети для отличия сгенерированных данных от настоящих. На практике они генерируют достаточно правдоподобные изображения, но страдают от так называемого схлопывания мод (mod collapse): может появиться такое пространство изображений, в котором они ничего не генерируют. Кроме того, они обучаются алгоритмом backpropagation, так что сложно представить их работу в коре головного мозга.

FF можно рассматривать как частный случай GAN в котором каждый слой дискриминативной модели принимает свое собственное решение о правдоподобности данных, так что нужды в обратном распространении ошибки нет. Также нет необходимости использовать backprop для обучения генеративной сети, потому что она может переиспользовать веса дискриминативной модели. Единственное, чему должна научиться модель — как преобразовать скрытые представления в генерируемые данные, и нет необходимости в backpropagation при использовании линейного преобразования для вычисления softmax логитов. Такой подход поможет избавиться от схлопывания мод и от проблемы, когда одна модель учится быстрее другой.
Сон
Алгоритм Forward‑Forward гораздо проще было бы представить, если бы положительные данные обрабатывались во время бодрствования, а негативные — создавались нейросетью и обрабатывались во сне.
При использовании суммы квадратов активаций как функции добротности, чередование между тысячами обновлений весов на реальных данных и тысячами обновлений на искусственных данных работает только в случае очень низкой скорости обучения и очень высокого импульса. Возможно, что другая функция добротности позволит отделить положительную фазу от отрицательной и это, пожалуй, самый важный вопрос о FF как биологической модели.
Было бы интересно увидеть при разделении положительной и негативной фазы, как приостановка обучения на искусственных данных вела к эффекту, похожему на серьезный недостаток сна.
Смертные вычисления
С точки зрения затрат электроэнергии эффективный способ умножения активаций на матрицу весов — реализовать активации как напряжение и веса — как проводники. Их произведение — накапливающиеся со временем заряды. Это выглядит более разумно, чем гонять транзисторы с высоким электропотреблением для моделирования отдельных бит в двоичном представлении числа и выполнять O(n^2) побитовых операций для умножения двух n‑битных чисел. К сожалению, алгоритм backprop сложно реализовать так эффективно.
Современные компьютеры были спроектированы для безоговорочного следования инструкциям и с четкой границей между софтом и железом — так, чтобы программу, написанную на одном компьютере, можно было перенести на другой. Это делает программу бессмертной: знания не умирают, когда умирает железо.
Разделение софта от железа — один из фундаментальных принципов Computer Science, который дает множество преимуществ. Можно изучать программу, не влезая в тонкости электротехники или написать программу и скопировать ее на миллион компьютеров. Либо возможно вычислять производные на большом датасете, используя несколько копий модели, запущенных параллельно. Если вы готовы отказаться от бессмертности, тогда вы сможете сэкономить на электричестве и производстве компьютеров. В будущем возможно появление таких компьютеров, которые нужно обучать под конкретные задачи. Параметры, обученные на этих компьютерах, нельзя явно скопировать на другие компьютеры, так что их вычисления смертны — они умирают с железом.
По мнению Хинтона, если вы хотите, чтобы ваша нейросеть была энергоэффективной, то вам стоит использовать смертные вычисления. Такие вычисления осуществимы только с алгоритмом обучения, который может эффективно работать на аппаратном обеспечении, чья точная конфигурация неизвестна. Forward‑Forward в данном случае — многообещающий кандидат, хотя еще только предстоит узнать, как он поведет себя в больших архитектурах.
Пути развития
Исследование Forward‑Forward (FF) алгоритма только началось и многие вопросы остаются открытыми:
-
Может ли FF воспроизвести генеративную модель изображений или видео, которые достаточно хороши для генерации негативных данных для обучения без учителя?
-
Какую функцию добротности лучше использовать? Минимизация суммы активностей без возведения в квадрат, судя по последним результатам, тоже работает неплохо.
-
Какую функцию активации лучше использовать? Пока была исследована только ReLU.
-
Для пространственных данных — может ли FF выиграть от нескольких функций добротности, вычисляемых на основе отдельных областей изображения?
-
Для последовательных данных — можно ли использовать быстрые веса (fast weights) чтобы мимикрировать упрощенный трансформер?
Официальной реализации алгоритма пока нет в открытом доступе. Хинтон писал свой код на матлабе и не хочет делиться им с широкой публикой.
В 1986 году Хинтон с коллегами опубликовали статью об использовании backprop в обучении нейросетей. Все относились к этому алгоритму довольно скептически до появления GPU с возможностью обучения на больших датасетах. Возможно, звездный час FF наступит гораздо раньше.
Теперь вы знаете, как работает алгоритм Forward‑Forward, какие преимущества и недостатки имеет, а также — как он симулирует поведение настоящих нейронов в мозге. Если в вас живет дух исследователя, уверены, что вам захочется разобраться в этой теме подробнее и модифицировать алгоритм для решения своих задач.
ссылка на оригинал статьи https://habr.com/ru/company/neoflex/blog/719496/
Добавить комментарий