
С момента выпуска ChatGPT я видел достаточно много статей о его способности писать код. Люди рассказывали о том, как они попросили его спроектировать и реализовать головоломку с числами (не зная, что «изобретённая» им игра уже существует) и как бот клонировал Pong; и даже я сам использовал его для создания нескольких простых вспомогательных скриптов на Python. Это очень мощный и довольно полезный инструмент.
Но во всех примерах, которые публиковали эти люди, было нечто общее. Все эти задачи были решены раньше или являлись крайне несущественными модификациями таких задач. И хотя, откровенно говоря, программирование во многом буквально в этом и заключается — в соединении готовых решений и в подстройке готового кода под ваш конкретный сценарий использования, сложная часть программирования — это решение задач, которые никто ещё не решал.
Поэтому я решил протестировать бота на особенно сложной «алгоритмической» задаче, которую решил пару лет назад. Я выбрал нечто мелкое и изолированное, чтобы уместить в промпт ChatGPT, но с достаточным количеством тонких моментов, чтобы он, по моему мнению, испытал бы проблемы с реализацией.
ЗАДАЧА
Давайте начнём с описания реальной задачи. В игре Mewgenics возможности движения используют поиск путей для перемещения кошки из начальной в конечную точку.

У кошки есть показатель максимальной дальности движения (в данном случае 6), а клетки имеют стоимость (в данном случае 1 для обычных клеток и 9999 для непреодолимых препятствий). Также есть клетки с водой, прохождение по которым стоит 2 единицы.
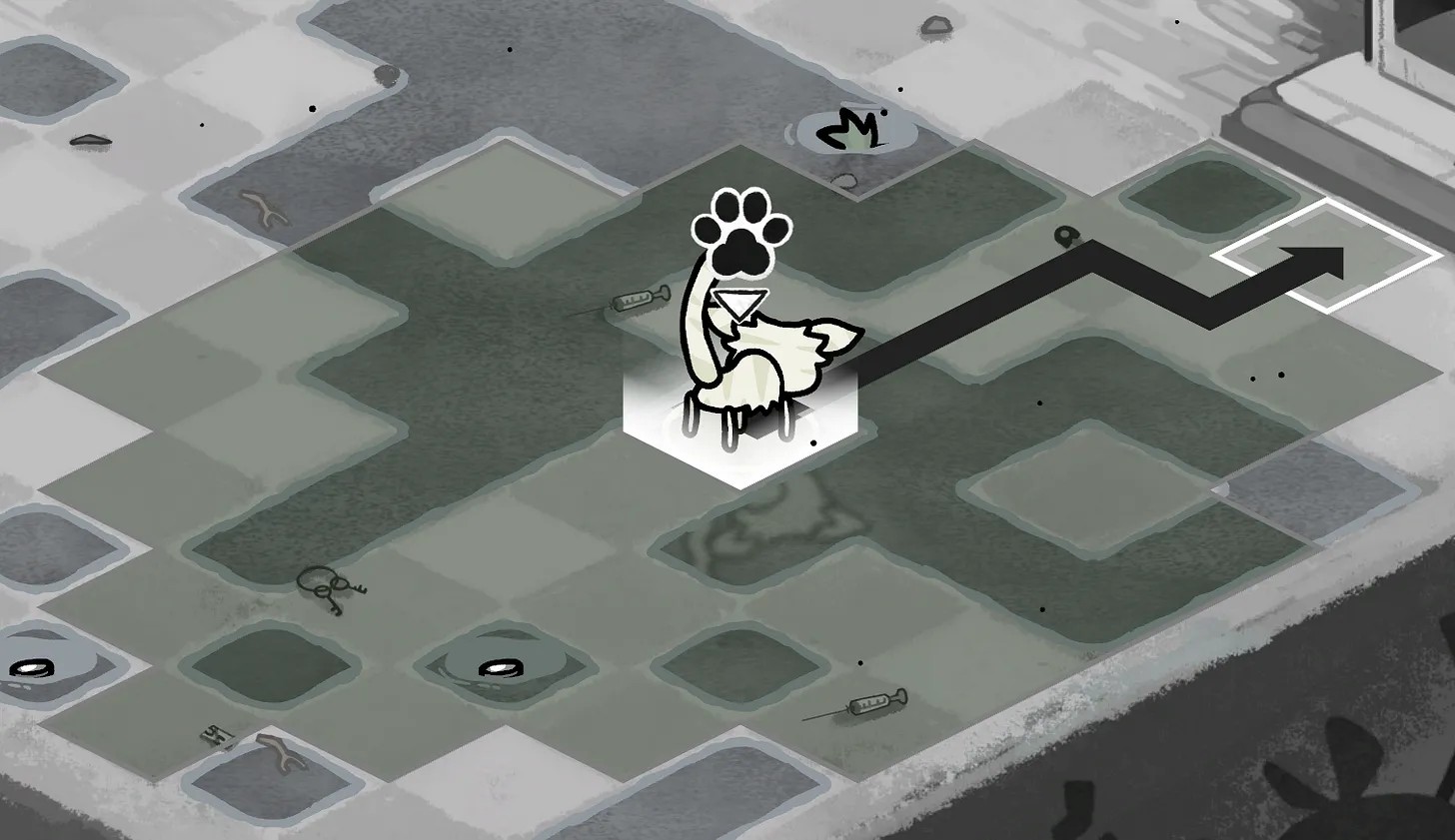
Пока всё описанное мной вполне привычно для поиска путей на сетке. С клетками, имеющими разную стоимость перемещения прекрасно справляются и алгоритм Дейкстры, и A*, а чтобы учесть максимальную дальность перемещения, достаточно лишь обрезать путь после определённого расстояния.
Сложность возникает, когда мы добавляем огонь (и другие типы клеток с опасностями). Клетки огня не требуют дополнительных трат для прохождения, как в случае с клетками воды, однако кошка стремится избегать прохождения по огню, если это возможно. На рисунке ниже показано работающее решение этой задачи. Существует также множество более сложных случаев; если клеток огня много, кошка должна пройти по наименьшему их количеству, и тому подобное. Моё решение работает хорошо.
Пока всё ещё не совсем понятно, почему эта задача сложна. Или, по крайней мере, почему решение сложнее, чем обычный алгоритм A* с модифицированной эвристикой, учитывающей «затраты на желание» прохождения, например, через огонь. Эта задача очень незначительно отличается от стандартного поиска путей при помощи A*, а решение, хотя и очень близко к A*, содержит несколько неинтуитивных изменений, которые очень важны. Это была «сложная» задача, и в 2020 году, когда я начал добавлять клетки огня в игру, для правильного решения этой проблемы с поиском путей мне потребовалась пара дней. Основная сложность заключается в ограничивающем факторе «максимальной дальности движения» и того, как он взаимодействует с затратами на путь через клетки и «затратами на желание», используемыми для избегания клеток с опасностями. В показанной выше анимации видно, как меняется путь, когда игрок пытается двигаться всё дальше и дальше от клетки огня: в определённый момент обойти её становится невозможно за 6 единиц движения, поэтому придётся идти сквозь огонь.
И если взять более изощрённые случаи, тоже возникает множество сложностей:


14 единиц движения или 10 единиц движения на одном уровне
В A* и алгоритм Дейкстры встроено предположение о том, что если кратчайший путь из A в C проходит через клетку B, то по такому же маршруту будет проходить кратчайший путь из A в B. Поэтому если вы уже нашли кратчайший путь до B, то можно просто продолжить оттуда и довести путь до C. Эти алгоритмы основываются на таком предположении, чтобы быть эффективными, потому что можно пропускать клетки, к которым уже найден более короткий путь при выталкивании из очереди с приоритетами, а при воссоздании пути в конце можно положиться на то, что каждая клетка хранит клетку, из которой в неё попали при помощи алгоритма поиска путей.
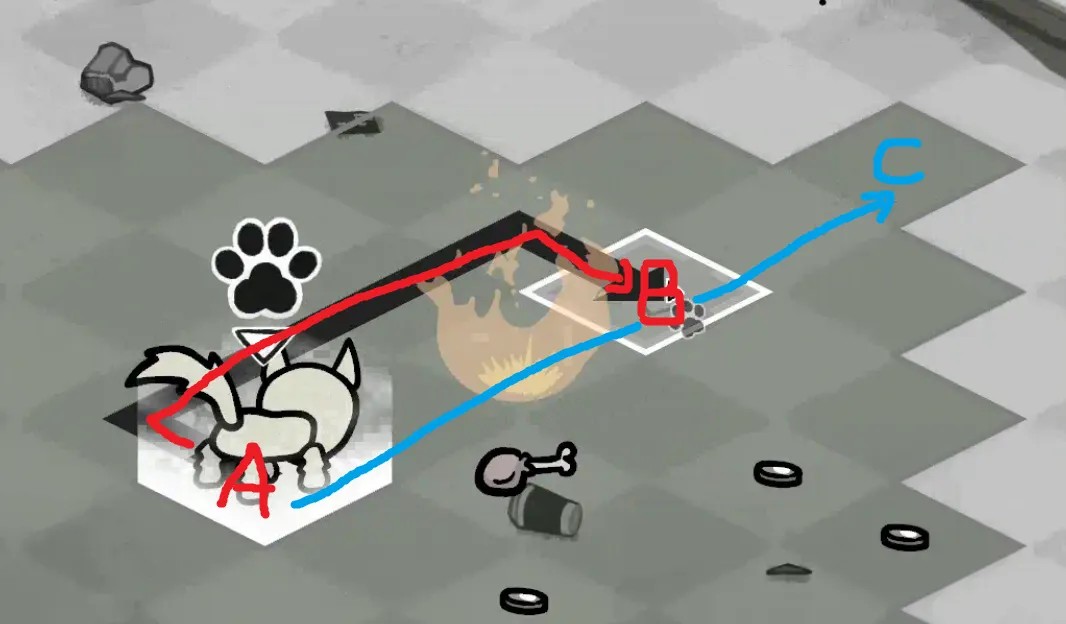
Вот о чём я говорю: показанная выше ситуация не происходит при «стандартном» поиске путей! Лучший путь из A в B не является частью лучшего пути из A в C, несмотря на то, что путь из A в C содержит клетку B. Это всё усложняет и разрушает предположения, на которые полагаются алгоритмы поиска путей.
МОЁ РЕШЕНИЕ
Итак, это ведь A* или алгоритм Дейкстры с модифицированными затратами и эвристиками? Ну… почти, но не совсем. Ниже показан код моего решения (вместе с дополнительными тонкостями для минимизации изгибов пути). Вы заметите, что это не совсем алгоритм Дейкстры или A*, и в коде есть много неочевидных вещей. На самом деле, я писал его в 2020 году и подробности уже забылись, поэтому даже мне неочевидно, почему он устроен именно так. Чтобы заставить его работать, потребовалось много проб и ошибок, я перемещал блоки и вносил небольшие изменения в алгоритм. Готовя этот пост, я дважды его проверил и попытался откатить его назад, попробовав снова превратить в модифицированный A*, однако любое внесённое для упрощения изменение лишь добавляло множество багов поиска путей. Поэтому я оставил его таким, каким он был. А ход размышлений, приведший меня к этому результату, практически стёрся из моего разума, потому что код и так уже работал.
Почему путь хранится внутри ячеек, добавляемых в очередь с приоритетами, а не как в стандартном A*, где узлы хранят информацию о том, из какого узла до них добрались? Почему код проверяет, является ли путь наилучшим, при выталкивании из очереди, а не при проталкивании в очередь? Обе эти особенности обеспечивают достаточно сильное отхождение от A*, но, очевидно, абсолютно необходимы для работы этого кода.
[Код содержит двунаправленный Unicode-текст, который может интерпретироваться или компилироваться иначе, чем показано ниже. Чтобы изучить его, откройте файл в редакторе, отображающем скрытые символы Unicode.]
struct advanced_weighted_cell { iVec2D cell; int cost; int desire; int bends = -1; temppodvector<char> current_path; int path_value() const { return cost*100+bends; } std::weak_ordering operator <=>(const advanced_weighted_cell& rhs) const { if(desire != rhs.desire) return desire <=> rhs.desire; if(cost != rhs.cost) return cost <=> rhs.cost; if(bends != rhs.bends) return bends <=> rhs.bends; return std::weak_ordering::equivalent; } }; podvector<iVec2D> TacticsGrid::advanced_pathfind(Character* source, iVec2D begin, iVec2D end, int max_range, bool sunken_only){ max_range *= pathfind_cost_resolution; podvector<iVec2D> path; dynamic_grid<int> pathvalues(width, depth); for(auto& t:pathvalues) t = INT_MAX; if(!Debug.CheckAssert(pathvalues.in_bounds(begin)) || !Debug.CheckAssert(pathvalues.in_bounds(end))) { return path; } auto costs = pathfind_costs(source, sunken_only); std::priority_queue<advanced_weighted_cell, std::vector<advanced_weighted_cell>, std::greater<advanced_weighted_cell>> queue; queue.push({begin, 0, 0, 0}); int total_checked = 0; while(!queue.empty()){ auto tile = queue.top(); queue.pop(); if(tile.path_value() <= pathvalues[tile.cell]){ pathvalues[tile.cell] = tile.path_value(); if(tile.cell == end) { iVec2D current = begin; for(auto i : tile.current_path){ current += all_orientations[i]; path.push_back(current); } //Debug.DisplayVariable(total_checked); return path; break; } for(int i = 0; i<4; i++){ auto &v = all_orientations[i]; iVec2D t2 = v+tile.cell; if(pathvalues.in_bounds(t2)){ advanced_weighted_cell next = {t2, tile.cost+costs[t2].enter_cost + costs[tile.cell].exit_cost, tile.desire+(t2==end?0:costs[t2].desire_cost),// + iso_dist(t2-end), //heuristic is more efficient, but results in paths with non-optimal numbers of bends tile.bends}; if(tile.current_path.size() > 0 && i != tile.current_path.back()) next.bends++; if(next.cost <= max_range && next.path_value() <= pathvalues[t2]){ next.current_path.resize(tile.current_path.size()+1); //minimize reallocations if(tile.current_path.size() > 0) { std::memcpy(next.current_path.data(), tile.current_path.data(), tile.current_path.size()*sizeof(char)); } next.current_path.back() = i; queue.push(next); total_checked++; } } } } } return path; }Впрочем, всё это вводная информация по задаче. Вы можете попробовать решить её самостоятельно, если хотите ощутить всю её нетривиальность (или если вы думаете, что это на самом деле может быть A* с модифицированной эвристикой) (а если вы действительно хотите попробовать и «рекомендовать» мне способы улучшить код, то, пожалуйста, на самом деле реализуйте и проверьте его в контексте; также учтите, что я всё равно не буду использовать его, потому что он и так хорошо работает, тщательно проверен на тысячах различных случаев и не имеет никаких проблем с производительностью).
ПОСМОТРИМ, КАК СПРАВИТСЯ С НИМ CHATGPT
И вот, наконец, сама суть этой статьи: настоящий эксперимент.
Сможет ли GPT-4 (через ChatGPT Plus) действительно решить эту задачу?
Я попросил его:
Напиши функцию в коде, решающую следующую задачу:
Агенту нужно найти наилучший путь на сетке клеток размером 10×10 из своего текущего местоположения в целевую точку.
Дальность его перемещения ограничена 5 очками.
Перемещение по обычным клеткам стоит 1 очко, перемещение по клеткам воды стоит 2 очка.
Перемещение по клеткам огня стоит 1 очко, однако агент должен избегать путей через них, даже если это означает удлинение пути к конечной точке (при условии, что путь по-прежнему находится в пределах дальности перемещения).
Ради эксперимента я намеренно убрал подробности алгоритма, вместо этого передав боту описание задачи, которую нужно решить. Ведь с этого и начинается решение задачи, и мне было действительно любопытно: возможно, существует более очевидное или тривиальное решение, которое я упустил, поэтому лучше не мешать ходу рассуждений подробностями реализации. Также я не сказал, на каком языке писать код, поскольку предполагал, что бот будет работать лучше, если выберет Python, а не будет вынужден писать на C++. В конце концов, мне важен был только сам алгоритм.
ChatGPT ответил:
Для поиска оптимального пути с учётом затрат и ограничений можно использовать алгоритм поиска путей A*. Вот функция на Python, решающая эту задачу:
[Код содержит двунаправленный Unicode-текст, который может интерпретироваться или компилироваться иначе, чем показано ниже. Чтобы изучить его, откройте файл в редакторе, отображающем скрытые символы Unicode.]
import heapq class Tile: def __init__(self, x, y, tile_type): self.x = x self.y = y self.tile_type = tile_type def cost(self): if self.tile_type == "water": return 2 elif self.tile_type == "fire": return 1 else: return 1 def is_fire(self): return self.tile_type == "fire" def heuristic(a, b): return abs(a.x - b.x) + abs(a.y - b.y) def a_star_search(grid, start, goal, max_movement): frontier = [] heapq.heappush(frontier, (0, start)) came_from = {start: None} cost_so_far = {start: 0} while frontier: current = heapq.heappop(frontier)[1] if current == goal: break for neighbor in get_neighbors(current, grid): new_cost = cost_so_far[current] + neighbor.cost() if new_cost <= max_movement and (neighbor not in cost_so_far or new_cost < cost_so_far[neighbor]) and not neighbor.is_fire(): cost_so_far[neighbor] = new_cost priority = new_cost + heuristic(goal, neighbor) heapq.heappush(frontier, (priority, neighbor)) came_from[neighbor] = current return came_from, cost_so_far def get_neighbors(tile, grid): neighbors = [] for dx, dy in ((-1, 0), (1, 0), (0, -1), (0, 1)): x, y = tile.x + dx, tile.y + dy if 0 <= x < len(grid) and 0 <= y < len(grid[0]): neighbors.append(grid[x][y]) return neighbors def reconstruct_path(came_from, start, goal): path = [goal] current = goal while current != start: current = came_from[current] path.append(current) return path[::-1] def find_best_path(grid, start, goal, max_movement): came_from, cost_so_far = a_star_search(grid, start, goal, max_movement) if goal not in came_from: return None return reconstruct_path(came_from, start, goal)
То есть бот как бы понял задачу, однако вместо того, чтобы «избегать» огня, он просто… никогда не ходит через огонь.
Поэтому я сказал:
Этот код отказывается прокладывать путь через огонь. Он всё равно должен прокладывать путь через огонь, если это необходимо, чтобы достичь конечной точки в пределах дальности его перемещения.
Бот извинился и исправил функцию a_star_search следующим образом:
[Код содержит двунаправленный Unicode-текст, который может интерпретироваться или компилироваться иначе, чем показано ниже. Чтобы изучить его, откройте файл в редакторе, отображающем скрытые символы Unicode.]
def a_star_search(grid, start, goal, max_movement): frontier = [] heapq.heappush(frontier, (0, start)) came_from = {start: None} cost_so_far = {start: 0} while frontier: current = heapq.heappop(frontier)[1] if current == goal: break for neighbor in get_neighbors(current, grid): new_cost = cost_so_far[current] + neighbor.cost() + (1000 if neighbor.is_fire() else 0) if new_cost - (1000 if neighbor.is_fire() else 0) <= max_movement and (neighbor not in cost_so_far or new_cost < cost_so_far[neighbor]): cost_so_far[neighbor] = new_cost priority = new_cost + heuristic(goal, neighbor) heapq.heappush(frontier, (priority, neighbor)) came_from[neighbor] = current return came_from, cost_so_farИ снова не совсем то. Он не делает никакой разницы между штрафом за прокладывание пути через огонь и физические затраты за прокладывание пути через клетки, поэтому всё равно не будет прокладывать путь через огонь (поскольку из-за штрафа +1000 клетки огня сильно выходят за пределы максимальной дальности хода).
Я ещё несколько раз писал боту, заставил его сгенерировать тестовый случай и исправил ошибку среды исполнения, которая возникла, когда я попытался запустить код. Завершив на этом, я создал тестовый случай для чего-то простого, что достаточно очевидно завершится ошибочно. Я поменял в этом тестовом случае местами x и y, но не хотел спорить об этом, поэтому просто смирился (повторная генерация занимает довольно много времени).
[Код содержит двунаправленный Unicode-текст, который может интерпретироваться или компилироваться иначе, чем показано ниже. Чтобы изучить его, откройте файл в редакторе, отображающем скрытые символы Unicode.]
import heapq class Tile: def __init__(self, x, y, tile_type): self.x = x self.y = y self.tile_type = tile_type def cost(self): if self.tile_type == "water": return 2 elif self.tile_type == "fire": return 1 else: return 1 def is_fire(self): return self.tile_type == "fire" def heuristic(a, b): return abs(a.x - b.x) + abs(a.y - b.y) def a_star_search(grid, start, goal, max_movement): frontier = [] heapq.heappush(frontier, (0, 0, start)) came_from = {start: None} cost_so_far = {start: 0} counter = 1 while frontier: _, _, current = heapq.heappop(frontier) if current == goal: break for neighbor in get_neighbors(current, grid): new_cost = cost_so_far[current] + neighbor.cost() if new_cost <= max_movement and (neighbor not in cost_so_far or new_cost < cost_so_far[neighbor]): cost_so_far[neighbor] = new_cost priority = new_cost + heuristic(goal, neighbor) + (1000 if neighbor.is_fire() and not (current.is_fire() and neighbor == goal) else 0) heapq.heappush(frontier, (priority, counter, neighbor)) came_from[neighbor] = current counter += 1 return came_from, cost_so_far def get_neighbors(tile, grid): neighbors = [] for dx, dy in ((-1, 0), (1, 0), (0, -1), (0, 1)): x, y = tile.x + dx, tile.y + dy if 0 <= x < len(grid) and 0 <= y < len(grid[0]): neighbors.append(grid[x][y]) return neighbors def reconstruct_path(came_from, start, goal): path = [goal] current = goal while current != start: current = came_from[current] path.append(current) return path[::-1] def find_best_path(grid, start, goal, max_movement): came_from, cost_so_far = a_star_search(grid, start, goal, max_movement) if goal not in came_from: return None return reconstruct_path(came_from, start, goal) def create_tile_grid(letter_grid): tile_grid = [] for x, row in enumerate(letter_grid): tile_row = [] for y, tile_type in enumerate(row): if tile_type == "R": tile_row.append(Tile(x, y, "regular")) elif tile_type == "W": tile_row.append(Tile(x, y, "water")) elif tile_type == "F": tile_row.append(Tile(x, y, "fire")) tile_grid.append(tile_row) return tile_grid def test_case(letter_grid, start_coords, goal_coords, max_movement): grid = create_tile_grid(letter_grid) start = grid[start_coords[0]][start_coords[1]] goal = grid[goal_coords[0]][goal_coords[1]] path = find_best_path(grid, start, goal, max_movement) if path: print("Path found:") for tile in path: print(f"({tile.x}, {tile.y}) -> {tile.tile_type}") else: print("No path found within the movement range.") letter_grid = [ ["R", "F", "F", "F", "R", "R", "R", "R", "R", "R"], ["R", "R", "R", "R", "R", "R", "R", "R", "R", "R"], ["R", "R", "R", "R", "R", "R", "R", "R", "R", "R"], ["R", "R", "R", "R", "R", "R", "R", "R", "R", "R"], ["R", "R", "R", "R", "R", "R", "R", "R", "R", "R"], ["R", "R", "R", "R", "R", "R", "R", "R", "R", "R"], ["R", "R", "R", "R", "R", "R", "R", "R", "R", "R"], ["R", "R", "R", "R", "R", "R", "R", "R", "R", "R"], ["R", "R", "R", "R", "R", "R", "R", "R", "R", "R"], ["R", "R", "R", "R", "R", "R", "R", "R", "R", "R"], ] start_coords = (0, 0) goal_coords = (0, 3) max_movement = 20 test_case(letter_grid, start_coords, goal_coords, max_movement)В заданном тестовом случае, так как он завершается на клетке огня, код просто даже не пытается избегать клетки огня.
Я попросил бота исправить это и он выдал мне решение, которое снова полностью отказывалось прокладывать пути через клетки огня.
Я попросил исправить это, и он вернулся к тому, что было до этого.
Сделав ещё несколько кругов, я решил, что этого достаточно. Бот подобрался близко. Казалось, он понимал задачу, но не мог правильно её решить.
Помогло ли бы мне это в 2020 году? Скорее всего, нет. Я попытался взять его решение и воспользоваться своим слабеньким человеческим мозгом, чтобы превратить его в работающий код, но создаваемый им путь всегда был не совсем правильным, поэтому пользы в этом не нашлось. Повторюсь, модификации исходного A*, приведшие к реальному решению, были неочевидными, поэтому не очень поможет начинать с «обычного A*». Более того, GPT даже не осознаёт, что эта задача сложнее, чем просто «модифицированный A*», а эта догадка сэкономила бы мне время, когда я писал этот алгоритм.
Как бы то ни было, возможно, эта задача не подходит для GPT. В конце концов, A* — это чрезвычайно популярный алгоритм и в обучающих данных бота есть тысячи или миллионы его примеров, что, возможно, ограничивает слишком сильное отклонение от него, как бы вы ни пытались подталкивать и помогать.
ДРУГИЕ ПОПЫТКИ
Я попробовал снова с парой других «сложных» алгоритмов, написанных мной, и каждый раз ситуация была практически такой же. Бот часто всего лишь предлагал решения схожих задач и упускал тонкости, отличавшие конкретную задачу, а спустя несколько итераций он просто запутывался.
В следующем примере (это алгоритм разрешения действия «отбрасывание» в Mewgenics) он попросту упускал все подробности задачи, например, что нельзя позволить двум движущимся объектам перемещаться одновременно. Ситуация оказалась ещё более плачевной: когда я случайно попросил решить задачу не GPT 4, а GPT 3.5, он гораздо сильнее приблизился к реальному решению, чем GPT 4.
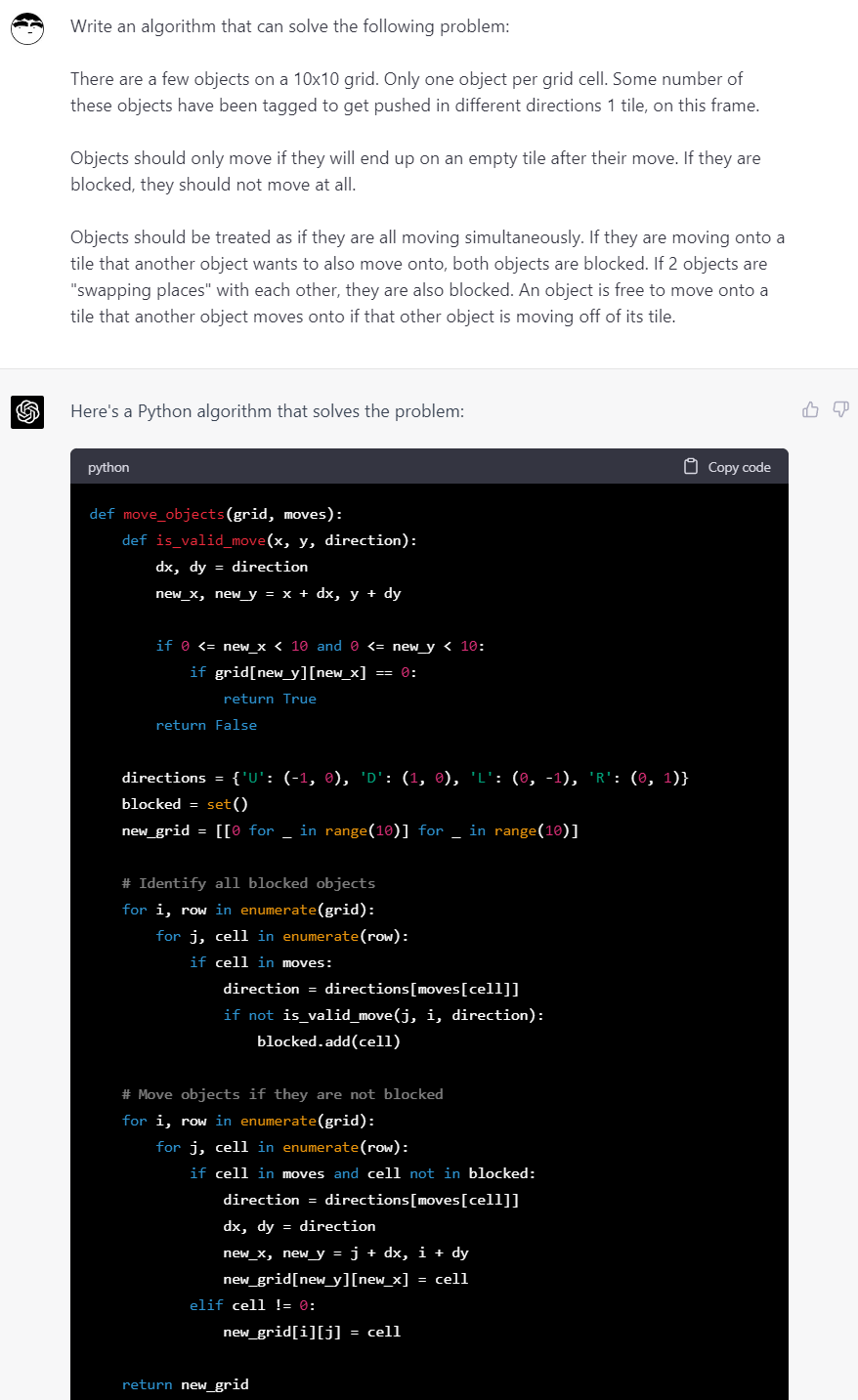
Напиши алгоритм, способный решить следующую задачу:
На сетке размером 10×10 есть несколько объектов. На одной клетке находится только один объект. Некоторое количество этих объектов помечено, они должны быть оттолкнуты в этом кадре в разных направлениях на 1 клетку.
Объекты могут перемещаться, только если после этого хода окажутся на пустой клетке. Если клетка заблокирована, они не должны двигаться.
Объекты должны обрабатываться так, как будто все они движутся одновременно. Если они движутся на клетку, на которую «хочет» сдвинуться другой объект, оба объекта остаются на месте. Если два объекта «обмениваются местами» друг с другом, то они тоже остаются на месте. Объект может перемещаться на клетку, где есть другой объект, если этот объект перемещается со своей клетки.
Ответ: Вот алгоритм на Python, решающий эту задачу
Мда… вообще мимо.
Когда я случайно попросил выполнить задачу GPT 3.5, он справился гораздо лучше. Это действительно «работающее решение, но с некоторыми багами и пограничными случаями». Оно не может обрабатывать цикл объектов, движущися друг на друга по цепочке, но да, это гораздо лучше, чем абсолютная ерунда, которую выдал GPT 4. Странно…

Модель: стандартная (GPT-3.5)
Напиши алгоритм, способный решить следующую задачу:
На сетке размером 10×10 есть несколько объектов. На одной клетке находится только один объект. Некоторое количество этих объектов помечено, они должны быть оттолкнуты в этом кадре в разных направлениях на 1 клетку.
Объекты могут перемещаться, только если после этого хода окажутся на пустой клетке. Если клетка заблокирована, они не должны двигаться.
Объекты должны обрабатываться так, как будто все они движутся одновременно. Если они движутся на клетку, на которую «хочет» сдвинуться другой объект, оба объекта остаются на месте. Если два объекта «обмениваются местами» друг с другом, то они тоже остаются на месте. Объект может перемещаться на клетку, где есть другой объект, если этот объект перемещается со своей клетки.
Ответ:
1. Создаём копию текущей сетки, чтобы не модифицировать исходную.
2. Создаём список объектов, которые помечены на перемещение.
3. Для каждого помеченного объекта проверяем, пуста ли целевая клетка. Если она не пуста или находится вне границ сетки, переходим к следующему объекту.
4. Для каждого непомеченного объекта проверяем, хочет ли он переместиться на целевую клетку помеченного объекта. Если да, помечаем оба объекта как заблокированные и переходим к следующему непомеченному объекту.
5. Для каждого непомеченного объекта проверяем, хочет ли он переместиться на текущую клетку помеченного объекта, который перемещается с неё. Если да, помечаем непомеченный объект как заблокированный и переходим к следующему непомеченному объекту.
6. Для каждого помеченного объекта, который не заблокирован, обновляем позицию в сетке.
7. Повторяем этапы 3-6, пока ни один объект не сможет больше двигаться.Вот псевдокод алгоритма:
Возможно, схожие задачи встречались в его обучающем датасете.
Сложно придумать действительно уникальные задачи, которые точно не имели ничего похожего раньше, или, по крайней мере, те которые можно описать одним-двумя абзацами. Давайте попробуем странный придуманный пример. Попросим бота создать алгоритм распознавания коллизий между… серпами лун. (После краткого гугления я не смог найти алгоритм для этого, и задача кажется довольно нетривиальной, так что попробуем её.)


Лунный серп можно определить как разность между двумя кругами. В коде он может храниться в подобной структуре:
struct crescent{ float outer_circle_x, outer_circle_y, outer_circle_radius; float inner_circle_x, inner_circle_y, inner_circle_radius; };Напиши алгоритм распознавания коллизий, получающий два серпа и возвращающий
true, если они пересекаются, иfalse, если не пересекаются.Ответ:
Для обнаружения коллизии между двумя серпами можно использовать следующий алгоритм:
1. Проверить любой из внешних кругов на коллизии.
2. Если у внешних кругов есть коллизии, проверить, любой из внутренних кругов на коллизии.
3. Если ни у одного из внутренних кругов нет коллизий, тогда серпы пересекаются.Вот реализация алгоритма распознавания коллизий на C++:
И затем он привёл код этого алгоритма. К чести ChatGPT, не сразу очевидно, в чём он ошибочен. Однако не так уж сложно найти контрпример.

У внешних кругов есть коллизия, у внутренних нет, но серпы не пересекаются.
Я попросил попробовать снова.

Неверно, существуют случаи, когда внешние круги пересекаются, внутренние круги не пересекаются и серпы тоже не пересекаются.
Ответ:
Вы правы, мой предыдущий ответ учитывал не все возможные случаи. Прошу прощения за то, что ввёл в заблуждение. Вот обновлённый алгоритм, который более точно проверяет коллизии между серпами:
1. Проверить любой из внешних кругов на коллизии.
2. Если внешние круги пересекаются, проверить следующие случаи:
a. Если оба внутренних круга внутри внешнего круга другого серпа и они не пересекаются, вернутьtrue(серпы пересекаются).
b. Если один внутренний круг находится внутри внешнего круга другого серпа и не пересекается с другим внутренним кругом, вернутьtrue(серпы пересекаются).
c. Если внешний круг одного серпа пересекается с внутренним кругом другого серпа, вернутьtrue(серпы пересекаются).
3. Если ничто из перечисленного выше не справедливо, то серпы не пересекаются.Вот обновлённая реализация на C++:
Очень сложно найти контрпримеры, но вот один, который не удовлетворяет 2.a (внешние круги пересекаются, каждый внутренний круг пересекается с внешним кругом другого, но не друг с другом, тем не менее, серпы не пересекаются):
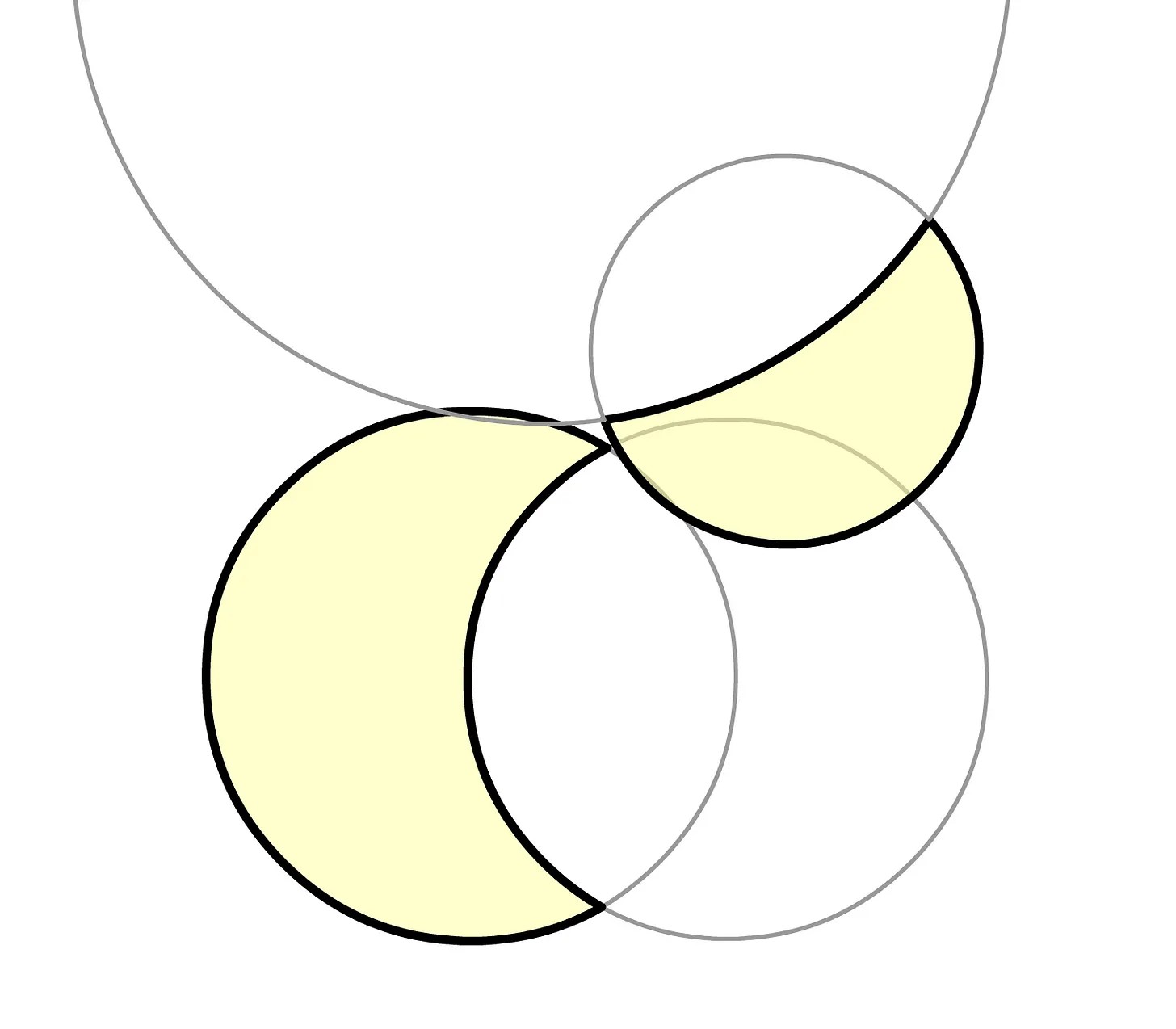
Мне кажется, ChatGPT уже вешает мне лапшу на уши. У него нет ответа и он не может его придумать, поэтому просто фантазирует. Впрочем… он неплохо фантазирует! Например, в этом алгоритме случаи, в которых он неверен, очень тонкие! Можно запросто опубликовать этот алгоритм в книге и сбить с толку людей, заставив их думать, что они что-то напутали в реализации, хотя на самом деле баги присутствуют в распознавании коллизий. Алгоритм выглядит именно так, как будто решает данную задачу.
ТАК МОЖЕТ ЛИ GPT-4 НА САМОМ ДЕЛЕ ПИСАТЬ КОД?
Если дать ему описание алгоритма или описание хорошо изученной задачи со множеством примеров в вебе, то да, GPT-4 совершенно точно умеет писать код. По большей мере он просто компилирует и перемешивает то, что видел, но, если честно, программирование во многом в этом и заключается.
Однако при попытке решить реальные задачи он совершенно теряется. Это те новые задачи, которые не были решены и с которыми вы можете столкнуться при программировании. Более того, бот любит «гадать» и на эти гадания вы можете потратить кучу времени, если он в решении задачи направит вас по неверному пути.
Вопиющим стал пример с серпами лун. ChatGPT не знает ответа, в его обучающем датасете не было нужного примера и он не может найти его в своей модели. В таком случае полезно было бы сказать: «Я не знаю алгоритма, способного это сделать». Однако он слишком уверен в своих возможностях и просто придумывает на ходу. Во многих других областях у него есть та же проблема, однако его странная компетентность в написании простого кода немного скрывает этот факт.
Как бы то ни было, по его собственным словам,

Напиши последний абзац к этой статье:
*Сюда я вставил весь текст своей статьи*
Ответ:
В заключение хочу сказать, что способность GPT-4 писать код впечатляет в контексте хорошо известных задач с готовыми примерами, однако он не оправдывает ожиданий при попытке решать новые или сложные алгоритмические задачи. Его чрезмерная уверенность и склонность к созданию убедительных, но неверных решений может сбивать с толку и приводить к лишним тратам времени. Хотя ChatGPT может быть ценным инструментом для решения простых задач, разработчики должны быть аккуратными и не полагаться на него в решении уникальных или сложных программных задач. Истинная суть программирования — решение новых задач — по-прежнему остаётся областью, в которой человеческая изобретательность превосходит ИИ, по крайней мере, пока.
ссылка на оригинал статьи https://habr.com/ru/post/723238/
Добавить комментарий