Введение
В настоящее время существует огромное количество всеразличного рода анонимных (скрытых) сетей, начиная с теоретически доказуемых (DC-сети, Queue-сети, Entropy-сети) и заканчивая практически используемыми (Tor, I2P, Mixminion). При таком количестве реализаций было бы очень удобно обобщить структуру всех таковых систем и привести их к общим составляющим. В результате подобных действий, мы сможем не только лучше понять то, как строятся современные анонимные сети, но и то, как их можно улучшать.
Теоретически доказуемая анонимность
Скрытыми сетями с теоретически доказуемой анонимностью принято считать замкнутые, полностью прослушиваемые системы, в которых становится невозможным осуществление любых пассивных атак (в том числе и при существовании глобального наблюдателя) направленных на деанонимизацию факта отправления и/или получения информации, или на деанонимизацию связи между отправителем и получателем с минимальными условностями по количеству узлов неподчинённых сговору. Говоря иначе, с точки зрения пассивного атакующего, апостериорные знания, полученные вследствие наблюдений, должны оставаться равными априорным, до наблюдений, тем самым сохраняя равновероятность деанонимизации по N-ому множеству субъектов сети.
DC-сети (проблема обедающих криптографов) являются наиболее классическими версиями анонимных сетей с теоретически доказуемой анонимностью. Он них можно почитать много где, включая википедию, а также в некоторых моих статьях, например здесь.
Queue-сети (задача на базе очередей) являются достаточно легкореализуемыми анонимными сетями с теоретически доказуемой анонимностью. О таковых я писал здесь, здесь, здесь, здесь, а также тут.
Entropy-сети (задача на базе увеличения энтропии) являются интересными сетями в плане теоретического анализа, но на практике сложнореализуемы из-за массы условностей, которые могут не учитываться в программных реализациях и, как следствие, приводить к проблемам деанонимизации. О таковых я писал здесь. Не путать с ENTROPY сетью.
Свойства и конструкты
В общих деталях, структура любой анонимной сети строится на определённо заданных шаблонах проектирования (далее, конструктах), а также дополнительных свойствах этих самых шаблонов. Конструкты описывают общий вид маршрутизации информации от точки A до точки B. Так как мы разбираем анонимные сети, то маршрутизация конечно же является запутывающей. Свойства конструктов способны дополнять саму маршрутизацию, обеспечивая задержки связи, накопление сообщений, периоды отправления и т.д.
Запутывающая маршрутизация
Маршрутизация в анонимных сетях не является примитивной и ставит эффективность распространения объектов опциональным параметром (низкие / высокие задержки), потому как главной целью становится создание запутывающего алгоритма (анонимизатора), который приводил бы к трудоёмкости анализа истинного пути от точки отправления до точки назначения. Производительность, эффективность «чистой» маршрутизации теряется, заменяясь особенностью алгоритма. В таких условиях, сами скрытые сети становятся медленными и сложными в применении (в том числе и с низкими задержками), что также частично или полноценно отодвигает их прикладное и повседневное использование в настоящее время.
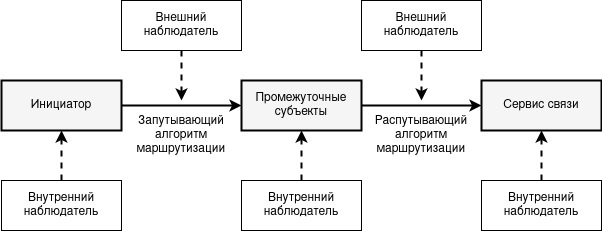
В задачах такого типа маршрутизации лежат модели угроз, в которых учитываются возможности атакующих. Главным антагонистом в подобных условиях становится государство, как внешний, глобальный наблюдатель, способный просматривать в широком масштабе распространение объектов по сети. В таком случае алгоритм маршрутизации должен уметь запутывать внешнего противника, не предоставлять возможности выявлять закономерности отправления, получения, запросов и ответов участниками анонимной сети. Другими, и не менее серьёзными противниками, являются внутренние атакующие, когда сами её же участники становятся отрицанием системы, её разложением. Предполагается, что внешние наблюдатели, помимо анализа трафика сети, способны также блокировать работающие узлы в системе, тем самым рассматривая их уникальные комбинации и паттерны поведения. Внутренние же наблюдатели способны наполнять сеть кооперируемыми узлами и совершать помимо маршрутизации также дополнительные действия, как отправление и получение информации. Наблюдатели без дополнительных функций называются пассивными атакующими, в противном случае – активными. В таких реалиях алгоритм маршрутизации должен отстранять буквально каждого субъекта (отправителя, получателя и промежуточного) от полноценного анализа принимаемой и отправляемой информации.
В начале исследования лучше будет разобрать сначала свойства, а лишь потом конструкты. Связано это с тем, что количество свойств уступает в величине количеству конструктов. При этом, каждый конструкт в своём исполнении всегда содержит свойства. Таким образом, сами свойства являются наименьшей, атомной величиной при анализе анонимных сетей.
Свойства
Отличительным признаком всех свойств друг от друга становится механизм выдачи итоговой информации на базе входной, принимаемой последовательности. Данные свойства обладают качествами, позволяющими им, в зависимости от задачи, предоставлять определённый уровень анонимности, производительности и/или применимости на практике.
-
«Поточность» Sp(f, X) = f(X). Если на вход алгоритму поступает информация X, тогда необходимое действие f, как ответ, должно выполняться сразу после обработки входной последовательности X. Представляет наилучшее качество производительности вычислений (в сравнении с другими свойствами) за счёт уменьшения качества анонимности. По количеству способов применения является лидирующим свойством. В качестве примера сеть Tor и луковая маршрутизация, которая не имеет каких-либо программных задержек при передаче информации между узлами.
-
«Периодичность» Tp(f, X, t) = t → f(X). Если на вход алгоритму поступает информация X, тогда необходимое действие f, как ответ, должно выполняться только после совершения периода равного t зависимого или независимого от времени поступаемой информации X. Может представлять высокое качество анонимности за счёт уменьшения качества производительности вычислений. Имеет самое малое количество способов применения из-за своих накладных расходов. В качестве примера можно привести сеть Herbivore и устанавливаемое расписание генерации.
-
«Аккумулятивность» Ap(f, Xi, k) = k → f(X1, X2, …, Xk). Если на вход алгоритму поступает информация Xi, тогда необходимое действие f, как ответ, должно выполняться только после принятия k-ого количества другой информации X. Представляет хорошее качество анонимности за счёт уменьшения качества производительности вычислений. Имеет ограниченное количество способов применения. В качестве примера сеть Mixminion и перемешанные сети (Mix networks).
В алгебраическом виде не только свойств, но и конструктов, первая заглавная буква всегда будет представлять наименование операции. Так например, «Поточность»=Stream=S, «Периодичность»=Time=T (здесь конечно со стороны английского период — это вовсе не время, но часто в научных и технических литературах период носит символ T), «Аккумулятивность»=Accumulative=A. Вторая прописная буква всегда будет представлять собой класс операции: свойство=property=p или конструкт=construct=c.
Конструкты
Конструкты условно можно разделить на три вида: генезис, базовые, составные. Генезис конструкт создаёт «почву» для формирования базовых конструктов, наиболее минимальных форм. Базовые конструкты формируют составные, с более конкретными уникальными свойствами, которые можно использовать в строении анонимных сетей.
1) Генезис конструкт
-
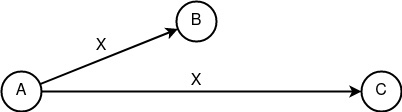
«Генерирование» Gc(X) = X. Генезис конструкт, представляющий факт генерации, инициализации или отправления информации X. Никаким образом не представляет анонимность, но является необходимой составляющей для инициирования всех действий. Таковой конструкт предполагает своё использование по умолчанию, потому как является прародителем всех последующих конструктов и следовательно обозначается просто как X.
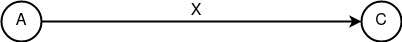
Генезис конструкт «Генерирование»
2) Базовые конструкты
-
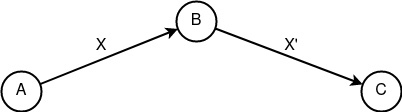
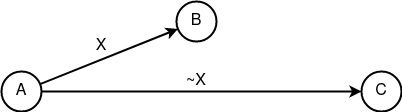
«Следование» Fc(X) = X’. Базовый конструкт, представляющий полиморфизм информации в своей простейшей форме. Лежит в основе VPN-сервисов и часто применяется анонимными сетями по причине простоты образования свойств несвязываемости между субъектами информации посредством объекта. Предполагается, что информация X’ — это более раскрытая версия информации X, и на примере множественного шифрования такое качество можно описать как X=E(E(M)), X’=E(M), X»=M и т.д., где M — открытое сообщение, а E — функция шифрования.
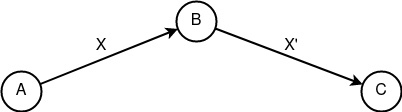
Базовый конструкт «Следование» Полиморфизм информации
Полиморфизм информации — свойство изменчивости передаваемого объекта при множественной маршрутизации несколькими субъектами сети, разграничивающее связь субъектов посредством анализа объекта. Так например, если существует три субъекта сети {A, B, C} и объект P, который передаётся от A к B и от B к C соответственно, то внешний вид информации P1 и P2 должен определяться как [P1 = (A → B)] != [P2 = (B → C)], где P ∉ {P1, P2}, P1 != P2, (B не связывает {P1, P2} с P) и (A не связывает {P1, P} с P2) и/или (C не связывает {P2, P} с P1). В большинстве случаев полиморфизм информации достигается множественным шифрованием объекта: [E2(E1(P)) = (A → B)] != [E1(P) = (B → C)], при котором интерстициальный субъект B становится неспособным связать {E2(E1(P)), E1(P)} с P, а субъект C неспособен связать {E1(P), P} с E2(E1(P)).
-
«Распространение» Dc(X, n) = (X)n. Базовый конструкт, представляющий собой в чистой форме широковещательную связь, за счёт которой появляется возможность сильного абстрагирования сетевой и криптографической идентификаций друг от друга, посредством слепой маршрутизации. Таковой конструкт можно наблюдать в приложении Bitmessage.
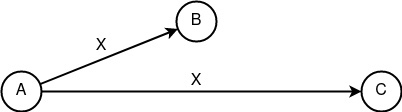
Базовый конструкт «Распространение» -
«Запутывание» Ec(n) = ~XG(n), где ~X = {~X1, ~X2, …, ~Xn} – множество всех ложных сообщение, n – количество всех возможных случайных сообщений, G – функция случайного выбора элемента из множества {1, 2, …, n}. Базовый конструкт, представляющий собой в чистой форме ложность факта отправления информации ~X. Невозможно применять в чистой форме из-за отсутствия самого факта передачи истинной информации, поэтому служит исключительно композитной частью для составных конструктов.
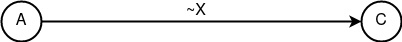
Базовый конструкт «Запутывание»
3) Составные конструкты
-
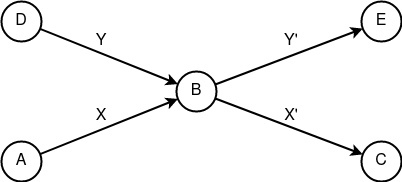
«Перемешивание» Pc(X, Y) = Fc(X, Y) = (Fc(X); Fc(Y)) = (X’; Y’). Составной конструкт, представляющий собой суммирование конструктов «следование». Позволяет улучшать критерий несвязываемости субъектов посредством неопределённости состояния передаваемого объекта. Такой составной конструкт можно наблюдать в Mixminion сетях, где основной упор делается как раз на перемешивание входной информации.
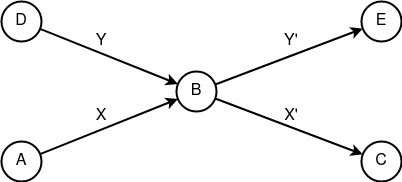
Составной конструкт «Перемешивание» -
«Расщепление» Sc(X, m, n) = (X; Dc(Ec(n), m)) = (X; (~XG(n))m). Составной конструкт, представляющий собой сочетание базовых конструктов «распространение» и «запутывание». Позволяет улучшать критерий несвязываемости субъектов посредством формирования ложных, запутывающих сообщений.

Составной конструкт «Расщепление» -
«Сведение» Mc(X, (~XG(n))m) = Mc(X, Dc(Ec(n), m)) = (X; Ø) = X. Составной конструкт, представляющий собой сочетание базовых конструктов «запутывание» и «распространение». По своей сути является обратным действием к составному конструкту «расщеплению».

Составной конструкт «Сведение»
Алгебраическое описание
Теперь, как только мы сформировали конструкты и понимаем их основную логику, мы можем начинать использовать и свойства, ориентируемые на данные конструкты. Так, в качестве примера, становится возможным формирование связи между конструктом «Генерирование» и свойством «Периодичность» следующим образом: GcTp = Tp(Gc, X, t). В таком случае, само отправление информации X (а точнее множества информаций вида Xi) от одного абонента к другому будет переодичным по времени t.
Также, конструкты, в отличие от свойств, имеют возможность накладываться друг на друга, или формировать определённые композиции своих функций. Так например, если существует некий абстрактный конструкт Ac, то невозможно применять одновременно операции типа AcSpTp, AcTpAp, AcApSp и т.д. Тем не менее, за счёт комбинации конструктов появляется возможность комбинировать и свойства. Так например, становится возможным применять разные свойства следующим образом: AcSp+AcTp. Плюс к этому существует возможность комбинировать конструкты с одним свойством по типу Ac1Ac2Tp.
В следствие этих наблюдений, можно заметить, что конструкты и свойства зависимы друг от друга, но имеют разные пропорции зависимостей, что легко наблюдается в возможности создавать N-ое количество конструктов с одним лишь свойством, но в невозможности создавать N-ое количество свойств с одним конструктом. Свзяно это в первую очередь с тем, что конструкты определяются наследованием предыдущих, более базисных конструктов.
Некоторые конструкты могут неявным образом порождать побочные конструкты, становясь в определённой степени динамичными структурами. Так например, базовый конструкт «следование» может неявным образом порождать составной конструкт «перемешивание». Некоторые анонимные сети оставляют такой критерий динамичности (Tor), другие напротив пытаются исключить «следование» и сделать «перемешивание» статичным конструктом (Mixminion). Связь между одним принципом и другим соблюдается лишь посредством выбора необходимого свойства. Так например, динамично порождаемое «перемешивание» является следствием свойства «поточность» конструкта «следование», в то время как статичный конструкт «перемешивание» обуславливается свойством «аккумулятивность».
Связь конструктов и свойств располагает также своими специфичными операциями. Предположим, что существуют некие множества абстрактных конструктов {#c1 , #c2, #c3, …, #cN} и абстрактных свойств {#p1 , #p2, #p3, …, #pN}, тогда можно выделить следующие операции.
-
«Сложение» (#c1#p1)+(#c2#p2) = #c1#p1+#c2#p2. Сложение является некоммутативной операцией, иными словами (#c1#p1)+(#c2#p2) ≠ (#c2#p2)+(#c1#p1), и неассоциативной, иными словами #c1#p1+(#c2#p2) ≠ (#c1#p1)+#c2#p2. Сложение выражает собой последовательные действия.
-
«Соединение» (#c1#p1);(#c2#p2) = (#c1#p1;#c2#p2) = #c1#p1;#c2#p2. В отличие от сложения, соединение объединяет два значения, не синтезируя их в одно. Является некоммутативной, но ассоциативной операцией.
-
«Произведение» n(#c#p) = (#c#p)+(#c#p)+…+(#c#p) (n раз) = #c#p+#c#p+…+#c#p (n раз). Произведение коммутативно, то есть n(#c#p) = (#c#p)n.
-
«Композиция» #c2(#c1#p1) = (#c2#c1#p1) = #c2#c1#p1. Композиция представляет собой объединение нескольких конструктов под одно свойство. Иными словами, аргументом свойства становятся последовательные действия конструктов #p1(#c2#c1). Операция коммутативна, то есть #c2(#c1#p1) = (#c1#p1)#c2. Исполнение конструктов внутри блока свойства происходит справа-налево.
Моделирование
На основе выстроенных конструктов и свойств, у нас появляется возможность создавать модели анонимных сетей. Основной нашей целью будет являться создание структур описывающих все возможные типы анонимизирующих связей, а именно: 1) анонимность отправителя или получателя, 2) анонимность отправителя и получателя, 3) анонимность связи между отправителем и получателем.
Типы анонимизирующих связей
-
Анонимность связи между отправителем и получателем. Представляет слабую модель угроз, потому как даёт возможность наблюдателям фиксировать факты отправления и получения информации истинными субъектами сети. Подобные системы несут малые накладные расходы, и, как следствие, могут применяться в довольно обширном множестве реализаций. Примером таковых сетей являются Tor, I2P, Mixminion.
-
Анонимность отправителя или получателя. Данная сеть имеет усреднённую модель угроз, в том плане, что таковая скрывает только факт отправления или только факт получения информации одним из субъектов (либо отправителем, либо получателем). Подобные системы могут быть хорошо применимы лишь в частных реализациях, как противопоставление анонимности по отношению ко второму субъекту, где не требуется защита отправителя (допустим при обращении к скрытому сервису через ботнет) или получателя (допустим при обращении к сервису в открытом Интернет-пространстве).
Примером таковых сетей может являться сеть, где отправитель транспортирует полностью зашифрованное сообщение всем участникам сети, расшифровать которое может только тот, у кого есть приватный ключ ориентированный на данное сообщение (если здесь конечно используется асимметричная криптография). Теоретически все могут узнать отправителя информации, но узнать получателя и есть ли он вообще крайне проблематично, потому как в теории получателем может оказаться каждый, т.к. каждый получает эти сообщения.
Другим примером может являться сеть, где по определённому периоду генерируется информация всеми участниками сети и отправляется одному серверу посредством нескольких несвязанных между собой общими целями и интересами (не находящимися в сговоре) маршрутизаторов. Получатель-сервер расшифровывает всю информацию и (как пример) публикует её в открытом виде, в следствие чего, все участники сети получают информацию от множества анонимных отправителей.
-
Анонимность отправителя и получателя. Представляет выражение сильной модели угроз, потому как скрывает единовременно и факт отправления, и факт получения информации. Так например, если предположить, что получателю всегда необходимо отвечать отправителю, иными словами воспроизводится модель типа «запрос-ответ», то в такой системе становится невозможным применить «анонимность отправителя или получателя», т.к. отправитель рано или поздно станет получателем, а получатель — отправителем, а потому и модель угроз на базе второго типа начнёт регрессировать и станет моделью на базе первого типа — «анонимность связи между отправителем и получателем». Подобные системы из-за своих вычислительных сложностей и ограничений часто являются малоприменимыми на практике. Примером таковых сетей могут служить DC-сети.
Первый пункт относится к критерию несвязываемости, в то время как второй и третий пункты к критерию ненаблюдаемости. Критерий ненаблюдаемости уже включает в себя критерий несвязываемости. Если пойти от обратного и предположить ложность данного суждения (то-есть, отсутствие несвязываемости в ненаблюдаемости), тогда можно было бы при помощи несвязываемости определить существование субъектов информации и, тем самым, допустить нарушение ненаблюдаемости, что является противоречием для последнего.
-
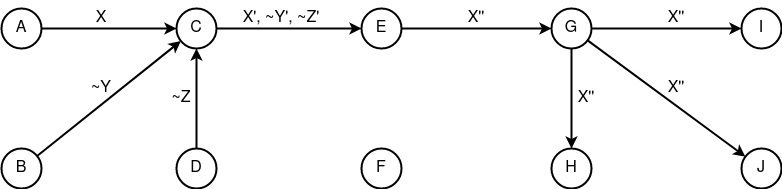
Пример модели сетевой коммуникации с анонимностью связи между отправителем и получателем на базе конструктов «следование» и динамического «перемешивания». Представителями такого вида коммуникаций можно считать сети Tor, I2P.
Если изменить свойство «поточность» на «аккумулятивность», то конструкт «перемешивание» станет статичным и основополагающим конструктом. Представителем уже такого усовершненствованного вида сетей становится сеть Mixminion.
n(FcSp)

Анонимность связи между отправителем и получателем -
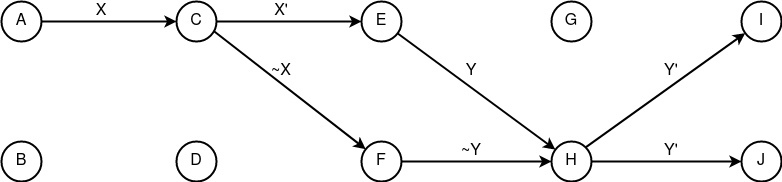
Пример модели сетевой коммуникации с анонимностью отправителя на базе конструктов «запутывание», «следование», «сведение» и «распространение». Безопасность приведённой концепции держится на узле «сведения» E, который должен обладать свойством «аккумулятивности» и на узлах {A, B, C}, которые должны обладать свойством «периодичности».
(FcTp;FcEcTp)+(McAp)+(DcSp)
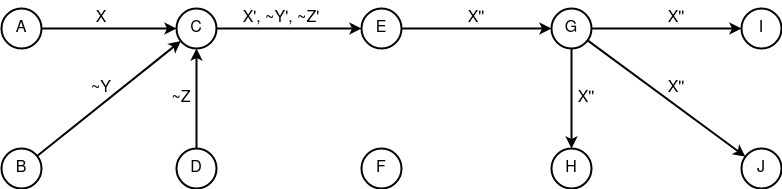
Анонимность отправителя -
Пример модели сетевой коммуникации с анонимностью получателя на базе конструктов «следование», «расщепление», «сведение» и «распространение». Безопасность приведённой концепции держится на узле «сведения» H, который должен обладать свойством «аккумулятивности».
(ScFcSp)+(DcMcAp)
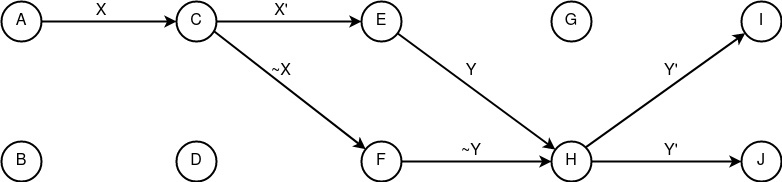
Анонимность получателя -
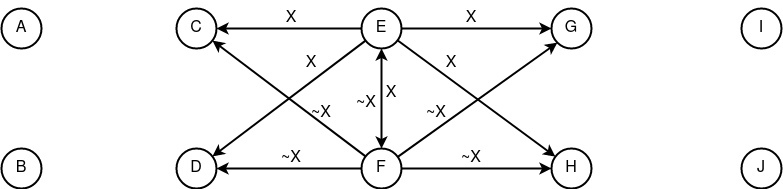
Пример модели сетевой коммуникации с анонимностью отправителя и получателя на базе конструктов «распространение», «запутывание» и «сведение». Безопасность приведённой концепции держится на всех узлах сети, которые должны обладать свойством «периодичности».
(DcTp;DcEcTp)+(McSp)
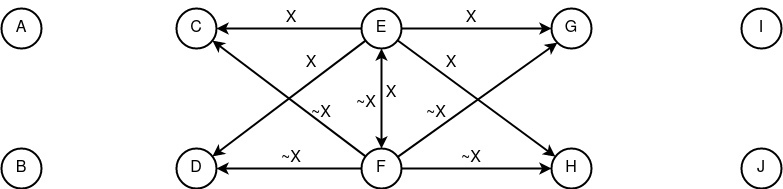
Анонимность отправителя и получателя
Примеры
Теория это хорошо, но когда дело не касается практики вовсе, то и сама теория становится бессмысленной. В таком контексте, можно разобрать некоторые детали проектирования анонимных сетей на программном уровне. В качестве примера я буду брать некоторые свои наработки. В качестве основы я возьму приложение HLS, базируемое на задаче очередей. Так как задача на базе очередей крайне легко описывается, то и пример будет простым и небольшим.
Задача на базе очередей
Вкратце суть задачи на базе очередей сводится к следующему: предположим,
что существует три участника {A, B, C}. Каждый из них соединён друг к
другу (не является обязательным критерием, но данный случай я привёл
исключительно для упрощения). Каждый субъект устанавливает время
генерации информации = T. У каждого участника имеется своё внутренее
хранилище по типу FIFO (первый пришёл — первый ушёл), можно сказать
имеется структура «очередь».
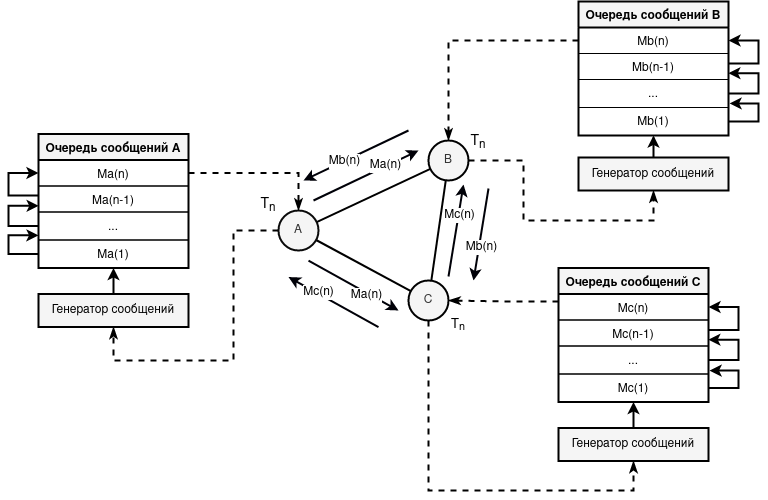
Предположим, что участник A хочет отправить некую информацию одному из участников {B, C}, так, чтобы другой участник (или внешний наблюдатель не знали, что существует какой-либо факт отправления. Каждый участник в определённый период T генерирует сообщение. Такое сообщение может быть либо ложным (не имеющее никакого фактического содержания и никому по факту не отправляется, заполняясь случайными битами), либо истинным (запрос или ответ). Отправить раньше или позже положенного времени T никакой участник не может. Если скопилось несколько запросов одному и тому же участнику, тогда он их будет ложить в свою очередь сообщений и после периода T достанет из очереди и отправит в сеть. Таким образом, сама структура задачи на базе очередей есть множество последовательно выстроенных очередей, в отличие от единственной очереди в DC-сетях.
Таким образом, внешний глобальный наблюдатель будет видеть лишь картину, при которой каждый участник в определённо заданный период времени T отправляет некое сообщение всем остальным узлам сети, что не даёт никакой информации о факте отправления, либо получения. Внутренние пассивные участники также неспособны узнать коммуниицирует ли один из участников в данный период времени с каким-либо другим, т.к. предполагается, что шифрованная информация не выдаёт никаких данных об отправителе и получателе непосредственно.
В общем виде, основной код представлен следующим образом.
for { msg, ok := <-p.GetMessageQueue().DequeueMessage() if !ok { break } var ( hash = msg.GetBody().GetHash() proof = msg.GetBody().GetProof() pubKey = p.GetMessageQueue().GetClient().GetPubKey() ) if err := p.networkBroadcast(pLogger, msg); err != nil { p.fLogger.PushErro(pLogger.GetFmtLog(anon_logger.CLogErroMiddleware, hash, proof, pubKey, nil)) continue } p.fLogger.PushInfo(pLogger.GetFmtLog(anon_logger.CLogBaseBroadcast, hash, proof, pubKey, nil)) }Метод DequeueMessage внутри себя уже содержит выставленный период взятия сообщений из очереди для последующего отправления всем узлам при помощи метода networkBroadcast. Таким образом, достигается связь вида DcTp. Если сообщений в DequeueMessage не существует, то данный метод берёт ложное сообщения из своего внутреннего пула и также его отправляет всем узлам при помощи метода networkBroadcast. За счёт этого, достигается уже связь вида DcEcTp. Каждый узел в сети придерживается этого правила, а потому и появляются параллельные действия вида (DcTp;DcEcTp).
sender, pld, err := p.GetMessageQueue().GetClient().DecryptMessage(msg) if err != nil { p.GetLogger().PushInfo(pLogger.GetFmtLog(anon_logger.CLogInfoUndecryptable, hash, proof, nil, pConn)) return }Обработка получаемой информации определяется в конечном итоге, как (McSp) = Mc(DcTp, DcEcTp), что приводит просто к удалению информации, которую мы не можем прочитать, и к получению валидной для нас информации.
Заключение
Итого, мы смогли выявить не только общие характеристики анонимных сетей, но и также смогли их комбинировать для выявление новых видов анонимизации, которых ранее могло просто не существовать на практике. Такой исход исследования способен дать большой просто действий, как со стороны дальнейших теоретических работ, так и со стороны практических реализаций анонимных сетей. Также более подробно, с теорией анонимных сетей, и скрытых систем в общем, вы можете ознакомиться тут, тут и здесь.
ссылка на оригинал статьи https://habr.com/ru/post/724824/
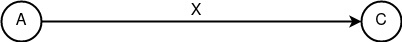
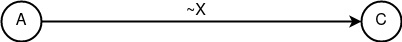


Добавить комментарий