Для чего
При изучении нейронных сетей встречается много новой теории и новых терминов. Это усваивается сильно лучше, если некоторое время «поиграть с параметрами». Поэтому мы взяли простой широкоизвестный датасет (MNIST, изображения рукописных цифр), простую однослойную FNN (Нейронная сеть прямого распространения) и подвигали параметры в разные стороны, отмечая и сравнивая, что происходит.
Конечно, непосредственно для распознавания и классификации изображений лучше применять не FNN (Нейронные сети прямого распространения), а CNN (Сверточные нейронные сети), в том числе и предобученные. С этим согласны, и целью данной статьи не является попытка превысить на FNN точность распознавания на CNN. В данной статьи мы просто подвигаем гиперпараметры и сделаем соответствующих выводы.
Полученные выводы могут быть действительно полезны и применимы впоследствии, когда для решения соответствующих задач будет необходимо «тюнить» предобученные сверточные сети — менять штатный классификатор (последние слои) на свой — в этом случае как раз и пригодится понимание применения гиперпараметров.
Общий подход
Общий подход такой: выбираем гиперпараметр и обучаем сеть, подставляя поочередно несколько значений. Тестируем несколько значений количества признаков, размера батча и так далее.
Подготовка данных
Подготовка данных происходит абсолютно стандартно, как и в большинстве роликов и статей по MNIST, поэтому особо не комментируем, просто прикладываем.
Библиотеки
import numpy as np import matplotlib.pyplot as plt %matplotlib inline import keras from keras.models import Sequential from keras.layers import Dense, Flatten, Dropout from keras.datasets import mnist from keras.callbacks import ReduceLROnPlateau from keras.callbacks import ModelCheckpoint Скачивание и преобразование данных
# Скачиваем данные и сразу распределяем на обучающую и тестовую выборки (x_train, y_train), (x_test, y_test) = mnist.load_data() # Преобразуем данные в интервал [0,1] x_train = x_train / 255 x_test = x_test / 255 y_train_cat = keras.utils.to_categorical(y_train, 10) y_test_cat = keras.utils.to_categorical(y_test, 10)Проверка корректности данных
# проверяем формы print(x_train.shape, y_train.shape, x_test.shape, y_test.shape) # выводим выбранный вектор данных из обучающей выборки print(x_train[7777]) выводим метку класса print(y_train[7777]) # выводим метку класса в one-hot-codding print(y_train_cat[7777]) # Выводим выбранное изображение plt.imshow(x_train[7777], cmap='binary') plt.axis('off') # без осей plt.show() # Выводим первых 25 изображений из обучающей выборки plt.figure(figsize=(20,10)) for i in range(25): plt.subplot(5,5,i+1) plt.xticks([]) plt.yticks([]) plt.imshow(x_train[i], cmap=plt.cm.binary) plt.show()Базовая комплектация сети
Берем самый простой стандартный вариант:
FNN: входной слой, один скрытый слой, выходной слой;
на выходе 10 нейронов (потому что 10 цифр = 10 классов);
функции активации — «relu» и «softmax» (стандарт);
функция потерь — «categorical_crossentropy» (стандарт, когда несколько классов);
метрика качества — «accuracy» (стандарт);
оптимизатор — «adam» (стандарт);
размер батча — 32 (надо с чего-то начинать);
размер валидационной выборки — 20% (стандарт).
Запускаем первый раз на 20 эпох и смотрим, что к чему.
model = keras.Sequential([ Flatten(input_shape=(28, 28, 1)), Dense(128, activation='relu'), Dense(10, activation='softmax') ]) model.compile( optimizer='adam', loss='categorical_crossentropy', metrics=['accuracy'] ) history = model.fit( x_train, y_train_cat, batch_size=32, epochs=20, validation_split=0.2 )Выводим цифры …
print('train:', model.evaluate(x_train, y_train_cat, verbose = 0)) print('test:', model.evaluate(x_test, y_test_cat, verbose = 0)) print( 'val_loss:', np.argmin(history.history['val_loss']), history.history['val_loss'][np.argmin(history.history['val_loss'])] ) print( 'val_accuracy:', np.argmax(history.history['val_accuracy']), history.history['val_accuracy'][np.argmax(history.history['val_accuracy'])] )train: [0.023798486217856407, 0.9946833252906799]
test: [0.09774788469076157, 0.9769999980926514]
val_loss: 7 0.08434651792049408
val_accuracy: 18 0.9779166579246521
… и графики.
plt.plot(list(range(1,len(history.history['loss'])+1)),history.history['loss']) plt.plot(list(range(1,len(history.history['val_loss'])+1)),history.history['val_loss']) plt.title("loss and val_loss") plt.grid(True) plt.show()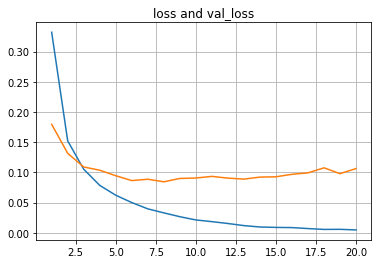
plt.plot(list(range(1,len(history.history['accuracy'])+1)),history.history['accuracy']) plt.plot(list(range(1,len(history.history['val_accuracy'])+1)),history.history['val_accuracy']) plt.title("accuracy and val_accuracy") plt.grid(True) plt.show()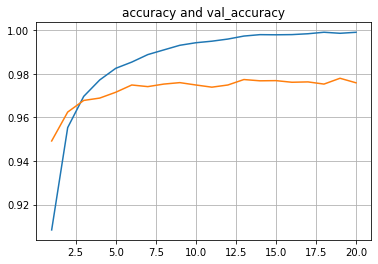
В первом приближении видим, что все «как по учебнику»:
ошибка на обучающей выборке уменьшается;
ошибка на валидационной выборке сначала уменьшается, потом увеличивается — переобучение;
точность на обучающей выборке подходит вплотную к 1.0;
точность на валидационной выборке доходит до 0.978;
точность на тестовой выборке 0.977.
Отсюда начинаем перебирать параметры.
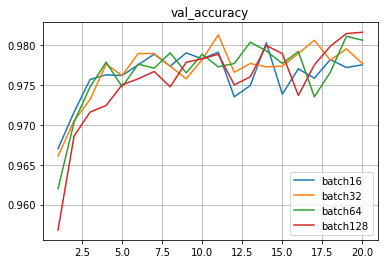
128 признаков, батчи 16-32-64-128

Видно, что чем больше размер батча, тем плавнее линии валидационной выборки.
Также видно, что при увеличении размера батча ошибка на валидацинной выборке задирается вверх меньше, прогиб смещается правее, то есть переобучение меньше.
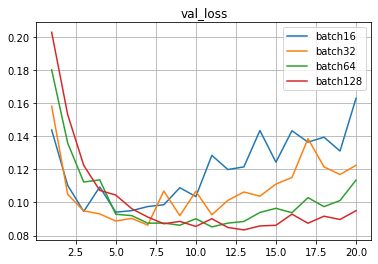
Точность на тестовой выборке у всеx очень близкая,
находится в интервале 0.9769-0.9789,
разница в десятые и сотые доли процента.
batch16: 0.9771999716758728
batch32: 0.978600025177002
batch64: 0.9789000153541565
batch128: 0.9768999814987183

256 признаков, батчи 16-32-64-128
Принципиально, ситуация та же, что и при 128 признаках.
Существенных изменений при переходе от 128 признаков к 256 не наблюдается.


Точность на тестовой выборке также очень близко,
находится в интервале 0.9795-0.9810,
что по сравнению с 0.9769-0.9789 (на 128) практически там же.
batch16: 0.9794999957084656
batch32: 0.9801999926567078
batch64: 0.9785000085830688
batch128: 0.9810000061988831

512 признаков, батчи 16-32-64-128
Ситуация с переобученностью стала более заметна.
Ошибка на валидационной выборке задирается вверх порезче.и прогиб смещается левее.
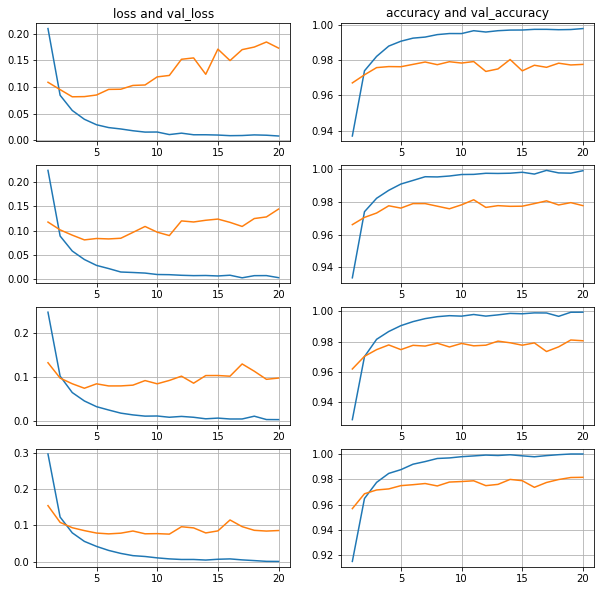

Точность на тестовой выборке также очень близко,
находится в интервале 0.9783-0.9824
что по сравнению с 0.9795-0.9810 (256) и 0.9769-0.9789 (128) практически там же,
хотя видно, что с увеличением числа признаков точность все таки на чуть-чуть повышается.
batch16: 0.9789000153541565
batch32: 0.9782999753952026
batch64: 0.9815000295639038
batch128: 0.9824000000953674
1024 признака, батчи 16-32-64-128
Ну и совсем для ясности сделаем замер на 1024 признака, и видим все то же самое.
Прогиб ошибки смещается левее из-за увеличившегося количества признаков, и смещается правее по мере увеличения размера батча.
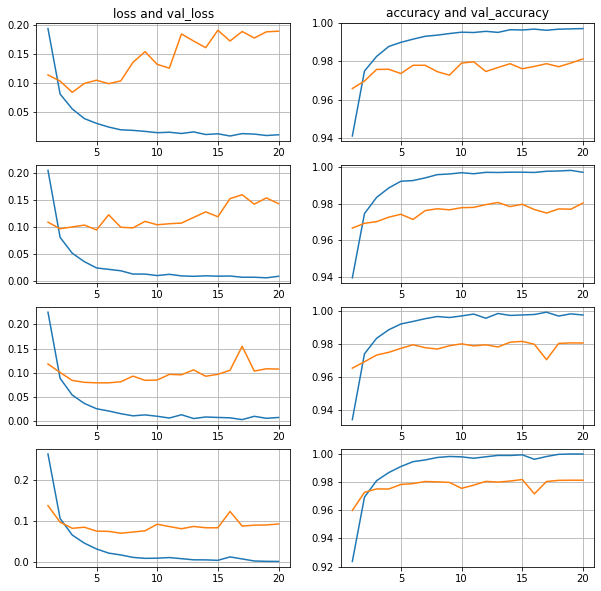

Точность на тестовой выборке также очень близко,
находится в интервале 0.9806-0.9841.
batch16: 0.9805999994277954
batch32: 0.9811999797821045
batch64: 0.982200026512146
batch128: 0.9840999841690063

Теперь заметнее, что при увеличении количества признаков точность в целом повышается:
128: 0.9769-0.9789
256: 0.9795-0.9810
512: 0.9783-0.9824
1024: 0.9806-0.9841.
Объединяем полученные данные
Ошибка (‘loss’) на тестовой выборке:
|
Признаки\Батчи |
16 |
32 |
64 |
128 |
|
128 |
0.1382 |
0.1004 |
0.0930 |
0.0860 |
|
256 |
0.1268 |
0.1047 |
0.0843 |
0.0742 |
|
512 |
0.1393 |
0.1253 |
0.0860 |
0.0717 |
|
1024 |
0.1615 |
0.1267 |
0.0957 |
0.0704 |
Точность (‘accuracy’) на тестовой выборке:
|
Признаки\Батчи |
16 |
32 |
64 |
128 |
|
128 |
0.9772 |
0.9786 |
0.9789 |
0.9769 |
|
256 |
0.9795 |
0.9802 |
0.9785 |
0.9810 |
|
512 |
0.9789 |
0.9783 |
0.9815 |
0.9824 |
|
1024 |
0.9806 |
0.9812 |
0.9822 |
0.9841 |




Предварительные выводы по количеству признаков и размерам батчей
Предварительные выводы следующие:
-
С увеличением размера батча линии валидационной выборки становятся плавнее.
-
С увеличением размера батча ошибка валидационной выборки задирается вверх меньше, прогиб смещается правее, то есть переобучение уменьшается.
-
С увеличением количества признаков ошибка валидационной выборки задирается вверх резче, прогиб смещается левее, то есть переобучение увеличивается.
-
С увеличением размера батча ошибка тестовой выборки в целом уменьшается.
-
В отношении точности тестовой выборки с увеличением размера батча неочевидно, в конечном итоге зависит от переобученности и количества признаков. При этом возможно подобрать такое количество признаков и такой размер батча, что точность будет выше.
-
С увеличением количества признаков ошибка тестовой выборки сначала падает, а потом или продолжает падать или начинает расти — переобучение. При этом чем меньше размер батча, тем выше уходит ошибка, и чем больше размер батча, тем меньше ошибка и может продолжать снижаться. То есть при увеличении количества признаков ошибка может уменьшаться при соответствующем подборе размере батча.
-
С увеличением количества признаков точность тестовой выборки в целом увеличивается, и это зависит от переобученности и размера батча.
-
Самые лучшие результаты в данном примере наблюдаются при максимальном количестве признаков (1024) по мере увеличения размера батча.
Берем сразу большой батч (batch1024)
На примерах выше видно, как линии сглаживаются при увеличении размера батча, а на размере 128 ошибка как бы зависает. Так и хочется взять батч еще побольше, чтобы ошибка двигалась вниз. Делаем скачок и берем размер батча 1024.



Можно сказать, что все ожидаемо:
1. линии гладкие;
2. ошибка валидационной выборки постепенно снижается;
3. линии ошибки идут ровненько одна за другой — чем больше батч, тем ниже линия:
4. линии точности также идут ровненько одна за другой — чем больше батч, тем выше линия
Дополнительно стало заметно, что пересечения линий обучающей и валидацонной выборок происходят левее, то есть раньше, по мере увеличения количества признаков.
Также видно, что здесь уже не хватает эпох и оптимум может быть где-то правее.
Таким образом становится понятен общий подход к подбору гиперпараметров:
1. увеличивать количество признаков;
2. под новое количество признаков подстраивать размер батча, чтобы сдвигать переобучение на более поздний срок;
3. отслеживать, когда происходит переобучение.
Альтернативный вариант — представить нейросеть, осуществляющую распознавание и классификацию, как функцию от соответствующих гиперпараметров, и надстроить отдельную «управляющую» нейронную сеть, определяющую оптимум данной функции стандартным для нейросети способом. Подбор гиперпарметров с помощью «управляющей» нейросети — тема для отдельной статьи.
Добавляем уменьшение шага
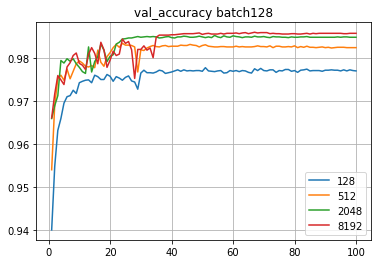
Запустим обучение с batch128 сразу на 100 эпох,
количество показателей 128-512-2048-8192.
Конечно, будет переобучение.
Существует функция, сохраняющая лучшие результаты (ModelCheckpoint). Однако наша задача — академическая, поэтому сохранять лучший результат не будем, просто смотрим графики 100 эпох, функцию прикладываем на случай, если понадобится.
сheckpoint = ModelCheckpoint('mnist-fnn.h5', monitor='val_acc', save_best_only=True, verbose=1)Понимая, что будет переобучение, добавим сразу уменьшение шага обучения.
Уменьшаем шаг обучения в два раза, если заданное количество эпох точность не повышается. При этом возможно задать и минимальное пороговое значение шага обучения.
reduce_on_plateau = ReduceLROnPlateau(monitor='val_accuracy', patience=3, verbose=1, factor=0.5, min_lr=0.0000001 )Из нескольких тестируемых комбинаций лучшая точность была 0.9869 (8192 признака, уменьшение шага в два разе, если в течение 3 эпох точность не увеличивается, ограничение на минимальный шаг обучение e-07).

Добавляем Dropout
Для сравнения:
20 эпох 1024 признака давали следующие значения точности :
batch16: 0.9806
batch32: 0.9812
batch64: 0.9822
batch128: 0.9841
100 эпох batch128 с уменьшением шага обучения давали следующие значения точности :
128 признаков: 0.9787
512 признаков: 0.9822
2048 признаков: 0.9849
8192 признака: 0.9869
С применением Dropout (0.1-0.2-0.3-0.4-0.5) 100 эпох, 1024 признака, batch128, без уменьшения шага — точность 0.9854 на Dropout 0.5.
За несколько итераций точность повысилась до 0.9860
(4096 признаков, batch512, Dropout 0.8, уменьшение шага в 2 раза, если 3 эпохи точность не поднимается).

Изначально допускаем, что во всех представленных случаях параметры не оптимальные, но вполне могут применяться для совместного сравнения.
Таким образом в ряде случаев (но не во всех) применение Dropout дает точность выше, чем без Dropout в случае переобучения, и сравнимую с уменьшением шага обучения при схожих количествах признаков и размерах батчей. Представляется, что наиболее вероятный ориентир для применения Dropout — уменьшение вычислений и соответствующее сокращение времени при достижении приемлемых и не самых высоких показателей точности.
Выводы
Выводы получились интересные.
1. Сеть мгновенно доходит до точности 97,7-97.8%, и такая точность достигается «легко и сразу».
2. Следующий 1% точности (до 98.7%) достигается уже с трудом, нужно подбирать.
3. Забегая вперед, можно сказать, что CNN дают точность выше 99.5%, но этот «крайний» процент (выше 99%) достигается уже с очень большим трудом.
Таким образом видно, что определенная «пороговая» точность (в данном примере порядка 97.7%) достигается достаточно уверенно и стабильно, и за этот показатель можно смело подписываться и заключать контракт, а вот после этого значения каждая десятая и даже сотая доля процента может потребовать существенных усилий.
Касательно общего алгоритма подбора краткий вывод получился такой:
Нужно брать количество признаков «побольше» (насколько позволяют вычислительные мощности и время) и следить, чтобы сеть не переобучалась. Для контроля переобучения подбирать размер батча и dropout, а для окончательного «шлифования» подбирать схему уменьшения шага обучения.
Что дальше
Вариантом развития представляется тестирование FNN в несколько слоев, а также тестирование CNN в несколько слоев с разными размерами ядер.
Отдельным вариантом развития является создание «управляющей» нейронной сети, которая «самостоятельно» будет подбирать архитектуру и гиперпараметры «контролируемых» нейронных сетей.
ссылка на оригинал статьи https://habr.com/ru/post/724418/
Добавить комментарий