Привет Хабр! В этой статье поработаем с аудиофайлами, используя библиотеку librosa и алгоритмы Machine learning.

Сначала немного поговорим о том, что такое аудиосигнал. Аудиосигнал представляет собой сложный сигнал, состоящий из нескольких одночастотных звуковых волн, которые распространяются вместе как изменение давления в среде. Каждый аудиосигнал имеет свои определенные характеристики, например, такие как частота, амплитуда, ширина полосы, децибел и т.д. Число волн, производимых сигналом за одну секунду называется частотой. Амплитуда показывает интенсивность звука, то есть является высотой волны. 

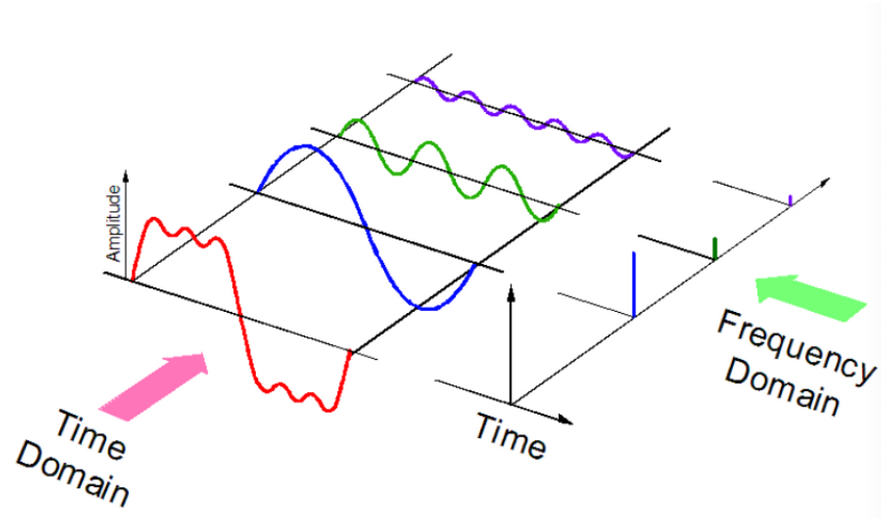
Можно сказать, что аудио является физическим представлением звука, частота которого находится в диапазоне от 20Гц до 20 килогерц.  Эти звуки доступны во многих форматах, что позволяет компьютеру их анализировать, например mp3, wma, wav.

Для работы с аудиосигналом его необходимо оцифровать, т.е. преобразовать звуковую волну в ряд чисел. Это делается путем измерения амплитуды звука через фиксированные промежутки времени. Каждое такое измерение называется выборкой, а частота выборки — количеством выборок в секунду. Например, обычная частота дискретизации составляет около 44 100 выборок в секунду. Это означает, что 10-секундный музыкальный клип будет содержать 441 000 семплов.

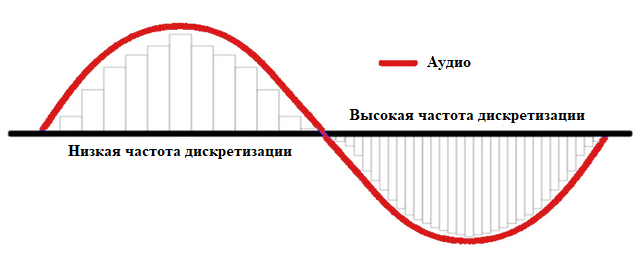
Благодаря дискретизации звука из аудиозаписей можно извлекать достаточно большое число различных характеристик, которые помогают в дальнейшем анализе аудио. Среди таких характеристик можно выделить, например, мел-кепстральные коэффициент (MFCCs), спектр, спектограмма, спектральный центроид (Spectral Centroid), спектральный спад (Spectral Rolloff)  и др.

Чтобы подробнее разобраться с данными характеристиками, установим библиотеку Librosa, которая используется для анализа звуковых сигналов, но больше ориентирована на музыку

pip install librosa

или

conda install -c conda-forge librosa

И здесь хочется сделать небольшое отступление. Я работаю в Jupyter Notebook и часто получается так, что ты набираешь эти волшебные команды и, …. ничего не работает. И тут тогда начинается, гуглишь, пробуешь различные варианты, которые обещают исправить проблему установки, пытаешься все переустановить заново, создать новую виртуальную среду, и все равно ничего не работает. Вот именно с этой библиотекой у меня было много проблем, в разные моменты времени появлялись разные ошибки и ничего не работало. Но потом, каким-то волшебным образом Librosa все-таки установилась, причем, я уже даже не знаю, что именно мне помогло.

Но есть предположение, что команда

.pip install librosa –-user оказалась волшебной.

Теперь можно импортировать библиотеку и начинать работать.

import librosa

Классификацию аудиофайлов будем проводить по набору данных, содержащим коллекцию из аудиофайлов по 10 различным жанрам. Каждый жанр имеет по 100 аудиофайлов продолжительностью по 3 и 30 секунд.

Загрузка аудио и извлечение значимых характеристик

Используя функцию librosa.load() можно считать конкретные звуки из нашего набора данных.

import os # библиотека для работы с файлами dir = '***/datasets/Data/genres_original' #задаем директорию с данными file = dir+'/blues/blues.00000.wav' signal, sr = librosa.load(file, sr = 22050) # загружаем файл

На выходе мы получаем два объекта,  первый — это цифровое представление нашего аудиосигнала (в виде временного ряда), второй — соответствующая частота дискретизации по которой он был извлечен. По умолчанию используется передискретизация 22050 Гц. Как говорилось выше частота дискретизации — это количество аудио семплов, передаваемых в секунду, измеряется в Гц или кГц.

print(signal.shape, sr) (661794,) 22050

Посмотрим на наш аудиосигнал

print(signal) [ 0.00732422  0.01660156  0.00762939 ... -0.05560303 -0.06106567  -0.06417847]

Полученный аудиосигнал можно представить в виде звуковой волны с помощью функции librosa.display.waveshow()

import matplotlib.pyplot as plt import librosa.display as ld plt.figure(figsize=(12,4)) ld.waveshow(signal, sr=sr)

Вертикальная сторона представляет амплитуду звука, а горизонтальная ось — время, затраченное на воспроизведение звука на определенной частоте.

А с помощью функции IPyhon.display() получим плеер в блокноте, где можно воспроизвести аудиофайл.

import IPython display(IPython.display.Audio(signal, rate = sr))

Звук можно перевести из временной области в частотную область с помощью быстрого преобразования Фурье таким образом, что после этого мы получим спектр сигнала. В librosa для этих целей есть функция librosa.stft() c такими параметрами как n_fft — длина оконного сигнала после заполнения нулями и hop_length — размер кадра или размер быстрого преобразования Фурье.

n_fft = 2048 ft = np.abs(librosa.stft(signal[:n_fft], hop_length = n_fft+1)) plt.plot(ft) plt.title('Spectrum') plt.xlabel('Frequency Bin') plt.ylabel('Amplitude')

Спектрограмма является визуальным способом представления уровня или громкости сигнала на различных частотах, присутствующих в формах волны. То есть показывает интенсивность частот во времени. Это дает представление времени по оси x, частоты по оси y, а соответствующие амплитуды представляются цветом

С помощью функции librosa.display.specshow() можно посмотреть на спектрограмму аудиосигнала:

X = librosa.stft(signal) s = librosa.amplitude_to_db(abs(X)) ld.specshow(s, sr=sr, x_axis = 'time', y_axis='linear') plt.colorbar()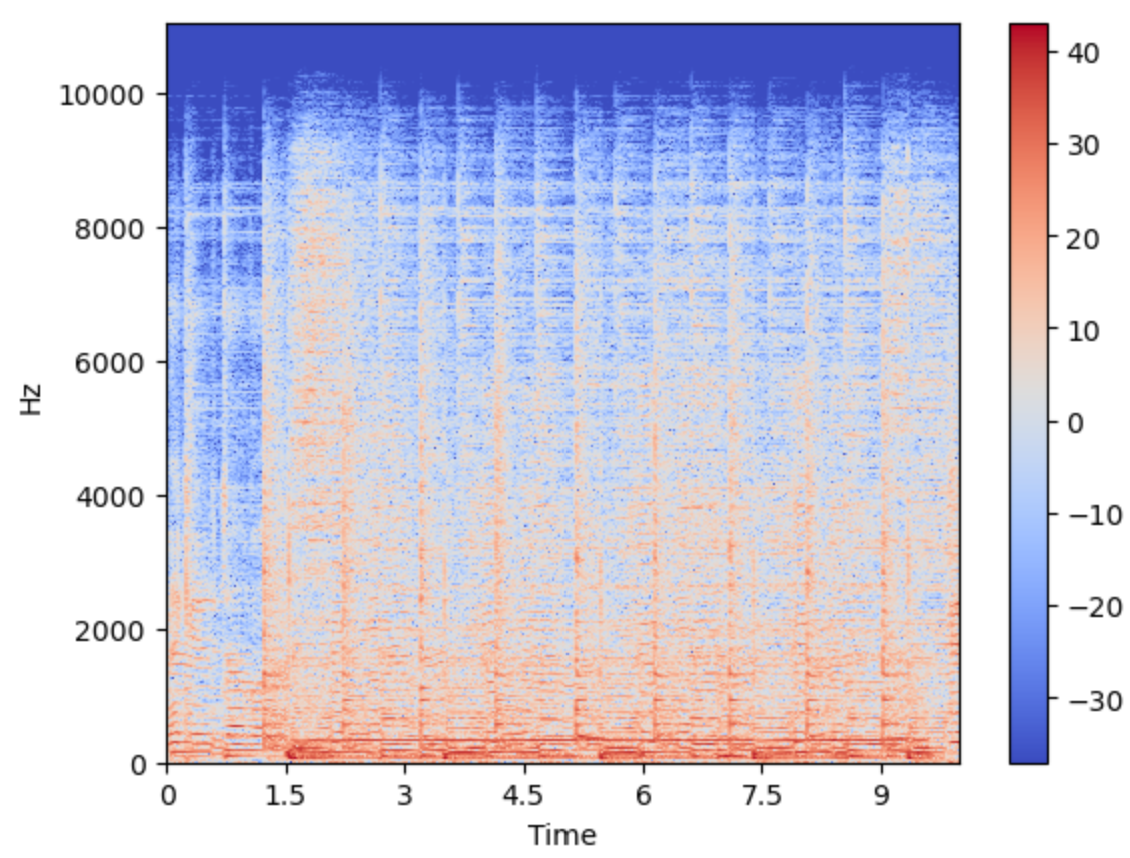

Мел-кепcтральные коэффициенты (MFCC) являются одним из важнейших признаков в обработке аудио. Процесс вычисления данных коэффициентов учитывает ряд особенностей слухового анализатора человека, моделируя характеристики человеческого голоса.  Это связано с тем, звуки, воспроизводимые человеком, определяется формой голосового тракта, включая язык, зубы и т.д.

Мел-кепcтральные коэффициенты можно найти с помощью функции librosa.feature.mfcc()

mfccs = librosa.feature.mfcc(y=signal, sr=sr, n_mfcc = 40, hop_length=512) mfccs

mfccs.shape (40, 1293)

n_mfcc — количество коэффициентов MFCC

hop_length — размер кадра

Размер матрицы мел-коэффициентов вычисляется как

[n_mfcc, len(signal)//hop_length+1]

То есть, если n_mels = 40, hop_length = 512, тогда

len(signal)//hop_length+1 = 661794//512+1 = 1292+1 = 1293.

Также мы можем построить мел-спектрограмму с помощью функции librosa.feature.melspectrogram(). Мел-спектрограмма представляет собой спектрограмму, преобразованную в мел-шкалу.

melspectrum = librosa.feature.melspectrogram(y=signal, sr = sr,                                         hop_length =512, n_mels = 40)

Спектральный центроид (Spectral Centroid) является хорошим показателем яркости звука, широко используется в качестве автоматической меры музыкального тембра. То есть центроид показывает где расположен центр масс звука. В блюзовых композициях частоты распределены равномерно, в металле спектроид лежит ближе к концу спектра. В Librosa используется функция librosa.feature.spectral_centroid()

cent = librosa.feature.spectral_centroid(y=signal, sr=sr) plt.figure(figsize=(15,5)) plt.semilogy(cent.T, label='Spectral centroid') plt.ylabel('Hz') plt.legend()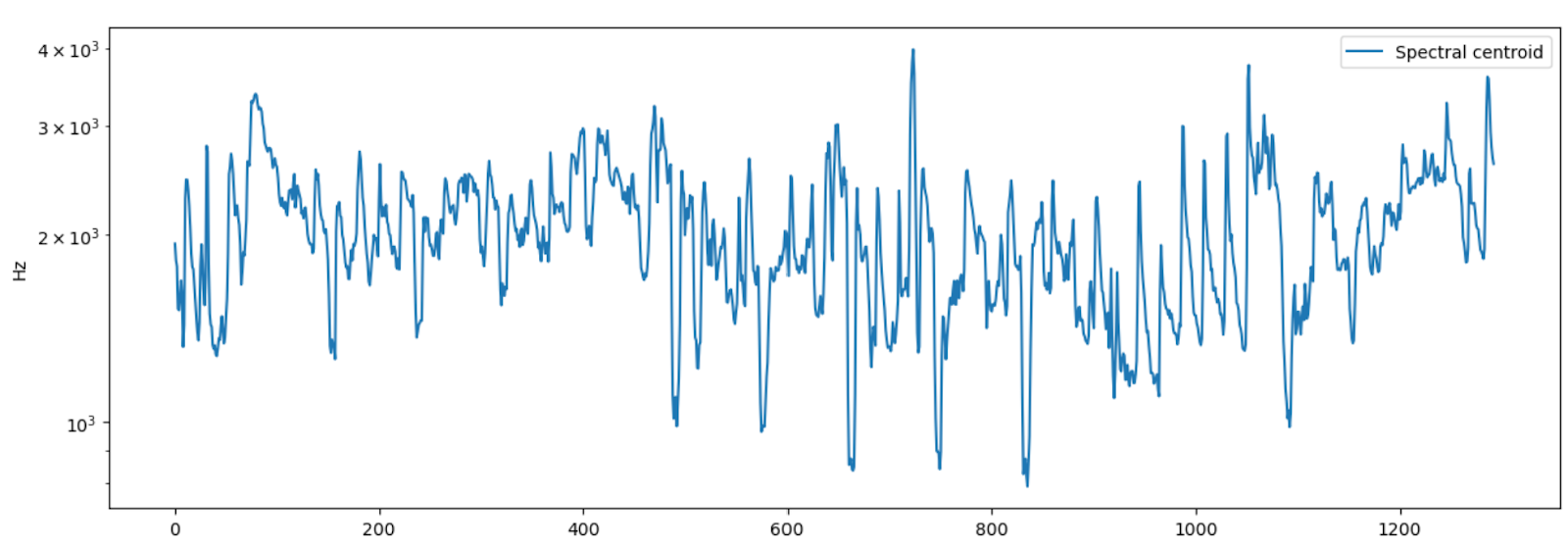

array([[1936.83283904, 1820.36294357, 1780.31673025, ..., 2770.21094705, 2661.92181327, 2604.75205139]])

Спектральны спад  (Spectral Rolloff) представляет собой частоту, ниже которой лежит определенный процент от общей спектральной энергии. В librosa используется функция librosa.feature.spectral_rolloff()

rolloff = librosa.feature.spectral_rolloff(y=signal, sr=sr) plt.figure(figsize=(15,5)) plt.semilogy(rolloff.T, label='Roll-off frequency') plt.ylabel('Hz') plt.legend()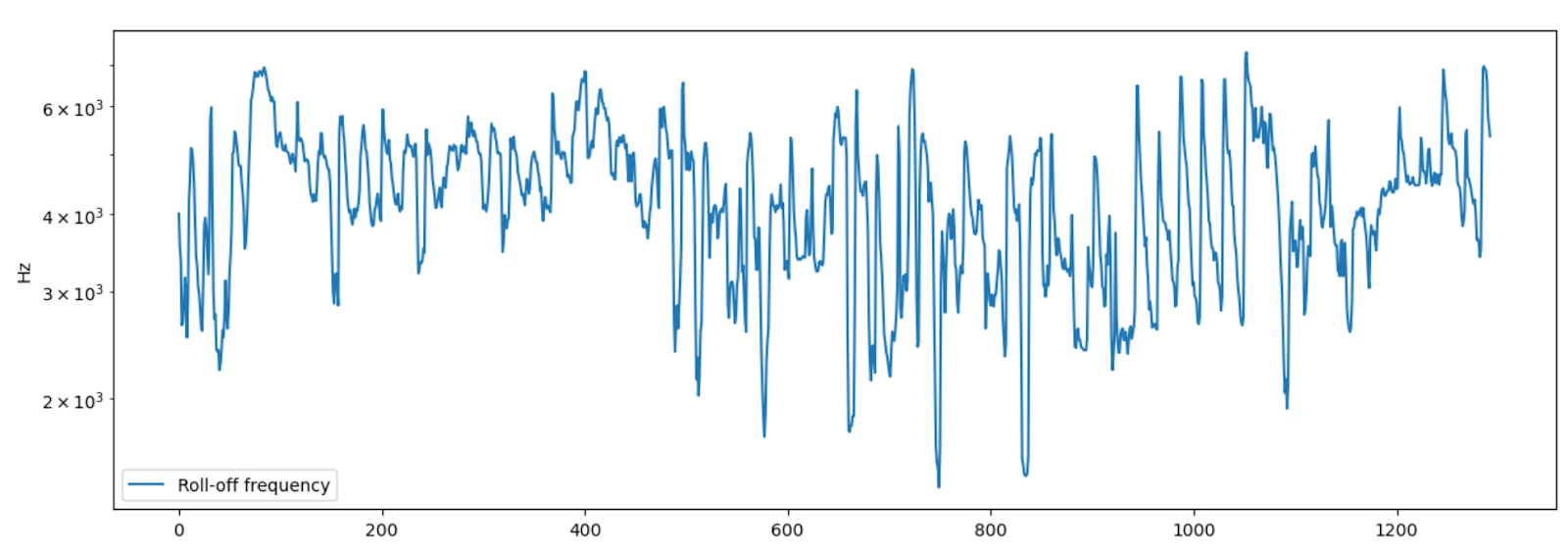

array([[4005.17578125, 3520.67871094, 3348.41308594, ..., 5792.43164062, 5577.09960938, 5361.76757812]])

Скорость пересечения нуля (Zero crossing Rate) является частотой изменения знака сигнала, то есть частота, с которой сигнал меняется с положительного на отрицательный и обратно. Например, для металла и рока этот параметр обычно выше, чем для других жанров, из-за большого количества ударных. В librosa используется функция librosa.feature.zero_crossing_rate()

zrate=librosa.feature.zero_crossing_rate(signal) plt.figure(figsize=(14,5)) plt.semilogy(zrate.T, label='Fraction') plt.ylabel('Fraction per Frame') plt.legend()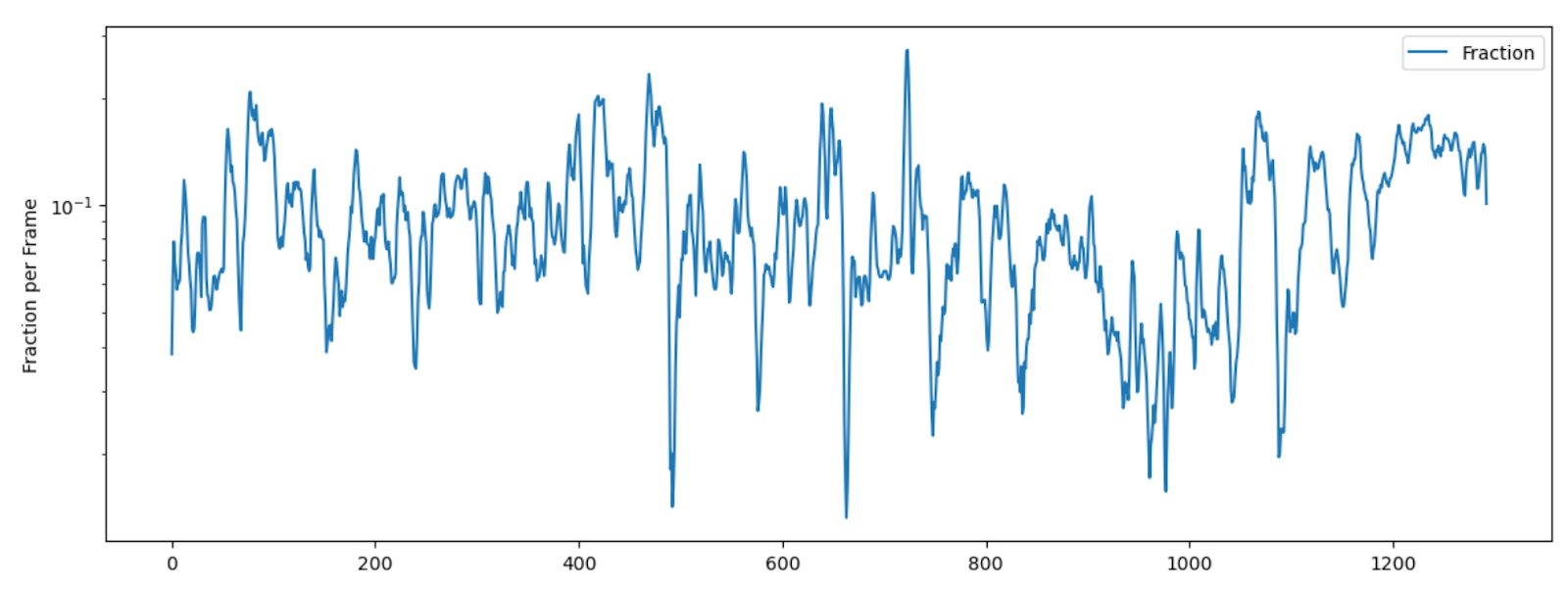

array([[0.03808594, 0.06054688, 0.07861328, ..., 0.14550781, 0.13623047, 0.10058594]])

Конечно, это далеко не весь перечень значимых характеристик аудиосигнала и обычно каждый исследователь выбирает сам какие характеристики для извлечения из аудиофайла он будет использовать в своей задаче. 

Например, можно также выбирать средние значения и стандартные отклонения мел-кепстральных коэффициентов:

mfcc_mean = np.mean(librosa.feature.mfcc(y=signal, sr=sr), axis=1) mfcc_std = = np.std(librosa.feature.mfcc(y=signal, sr=sr), axis=1)

средние значения и стандартные отклонения спектрального центроида

cent_mean = np.mean(cent) cent_std = np.std(cent)

средние значения и стандартные отклонения спектрального спада и т.д.

roloff_mean = np.mean(roloff) croloff_std = np.std(roloff)

Потом все эти значения можно записать в датафрейм и работать с ними

df = pd.DataFrame(audio_data) df['labels'] = labels

Для дальнейшего анализа необходимо выделить характеристики из всех аудиофайлов. Для этого, например, мы можем получить средние значения мел-кепстральные коэффициенты  для всех наших аудиофайлов. Сначала создаем список audio_files с названиями файлов всех композиций и соответствующие им метки labels типа жанра:

audio_files = [] labels = [] labelind = -1 for label in os.listdir(dir): labelind +=1 label_path = os.path.join(dir, label) for audio_file in os.listdir(label_path):     audio_file_path = os.path.join(label_path, audio_file)     audio_files.append(audio_file_path)     labels.append(labelind)

Теперь создадим функцию, которая на вход будет принимать аудиофайл, а затем получать средние значения коэффициентов  для данного файла.

def preprocess_audio(audio_file_path): audio, sr = librosa.load(audio_file_path) mfcc_mean = np.mean(librosa.feature.mfcc(y=audio, sr=sr),   axis=1) return abs(mfcc_mean)

Получим список audio_data цифровых значений для всех аудиофайлов:

audio_data =[] for audio_file in audio_files: mfccs_mean = preprocess_audio(audio_file) audio_data.append(mfccs_mean)

Создадим массивы из характеристик аудиофайлов и их меток

audio_data = np.array(audio_data) labels = np.array(labels)

Таким образом, можно все характеристики аудиофайлов объединить в один датафрейм и далее с ним работать. 

Построение модели

Набор данных, с которым я работаю уже содержит csv файл в котором содержится информация о мел-кепстральных коэффициентах, спектральных центроидах и т.д. Загрузим и посмотрим на него.

df = pd.read_csv(f'{dir}/features_3_sec.csv') df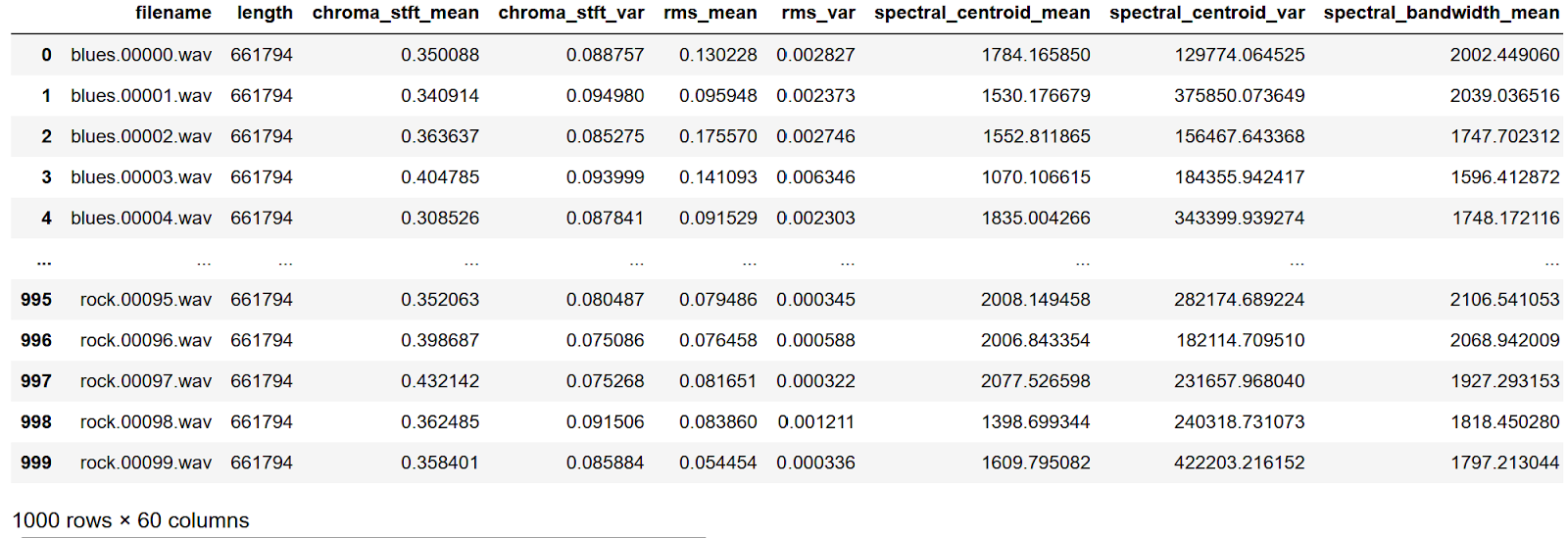

В нашем датафрейме 2 столбца (filename и length), которые далее нам не понадобятся, поэтому удалим их.

df = df.iloc[0:, 2:]

Теперь определим вектор с данными для обучения (X) и вектор соответствующим их меток (y). Данные для обучения представляют собой значимые характеристики аудиоданных, всего 57 значений. Разберемся с метками классов. 

df['label'].unique() array(['blues', 'classical', 'country', 'disco', 'hiphop', 'jazz',        'metal', 'pop', 'reggae', 'rock'], dtype=object)

Они имеют категориальное представление, поэтому преобразуем их в численное представление с помощью метода LabelEncoder().

class_list=df.iloc[:,-1] # создаем список классов convertor = preprocessing.LabelEncoder() y=convertor.fit_transform(class_list) # конвертируем признаки

Теперь перейдем к данным для обучения Х. Удалим из нашего датафрейма столбец с метками.

X = df.loc[:, df.columns !='label']

Нормализуем наш целевой вектор с помощью метода StandardScaler()

from sklearn import preprocessing cols = X.columns scaler = preprocessing.StandardScaler() np_scaled = scaler.fit_transform(X) X = pd.DataFrame(np_scaled, columns = cols)

Разделим выборку на тестовую и обучающую

from sklearn.model_selection import train_test_split X_train, X_test, y_train, y_test = train_test_split(X, y, test_size = 0.3, random_state=42 )

Воспользуемся классическими алгоритмами машинного обучения: алгоритм Байеса, логистическая регрессия, метод к-ближайших соседей, метод опорных векторов, ансамблевыми методами: случайный лес, XGBoost (деревья с градиентным бустингом) и моделью многослойного перспетрона MLPClassifier.

Импортируем необходимые модули:

from sklearn.naive_bayes import GaussianNB from sklearn.linear_model import LogisticRegression from sklearn.neighbors import KNeighborsClassifier from sklearn.ensemble import RandomForestClassifier from sklearn.svm import SVC from sklearn.neural_network import MLPClassifier from xgboost import XGBClassifier from sklearn.metrics import confusion_matrix, accuracy_score, roc_auc_score, roc_curve

Создадим дополнительную функцию по работе с алгоритмами обучения:

def model_assess(model, title = "Default"): model.fit(X_train, y_train) preds = model.predict(X_test) print('Accuracy', title, ':', round(accuracy_score(y_test, preds), 5), '\n')

Построим модели и оценим точность.

# алгорит Баейса nb = GaussianNB() model_assess(nb, "Naive Bayes") # алгоритм k-ближайших соседей knn = KNeighborsClassifier(n_neighbors=10) model_assess(knn, "KNN") # метод опорных векторов svm = SVC(decision_function_shape="ovo") model_assess(svm, "Support Vector Machine") # логистическая регрессия lg = LogisticRegression(random_state=0, solver='lbfgs', multi_class='multinomial') model_assess(lg, "Logistic Regression") # случайный лес rforest = RandomForestClassifier(n_estimators=1000, max_depth=10, random_state=0) model_assess(rforest, "Random Forest") # многослойный персептрон nn = MLPClassifier(solver='lbfgs', alpha=1e-5, hidden_layer_sizes=(5000, 10), random_state=1) model_assess(nn, "Neural Nets") # деревья с градиентным бустингом xgb = XGBClassifier(n_estimators=1000) model_assess(xgb, "XGBClassifier")

Видим, что самый низкий показатель точности 0,52 у алгоритма Байеса, а самый высокий 0,9 у алгоритма XGBClassifier.

Рекомендации аудиокомпозиций

А теперь попробуем  порекомендовать пользователю аудиокомпозиции, используя метод cosine_similarity() из библиотеки scikit-learn. Данный метод вычисляет косинусное сходство между двумя ненулевыми векторами и основан на косинусе угла между ними, что дает значение от -1 до 1. Значение -1 означает, что векторы противоположны, 0 представляет ортогональные векторы, а значение 1 означает подобные векторы.

Для этого возьмем csv файл, прочитаем его и удалим лишние столбцы.

df1 = pd.read_csv(f'{dir}/features_30_sec.csv',index_col=0) labels = df1[['label']] df1 = df1.drop(columns=['length','label'])

Далее переведем наш датафрейм в матрицу размером 1000х57 и вычислим косинусное сходство между векторами.

from sklearn import preprocessing from sklearn.metrics.pairwise import cosine_similarity scaled=preprocessing.scale(df1) similarity = cosine_similarity(scaled)

И теперь полученную матрицу сходства представим в виде датафрейма:

similarity_labels = pd.DataFrame(similarity) similarity_names = similarity_labels.set_index(labels.index) similatity_names.columns = labels.index

Теперь на основе полученного датафрейма мы можем рекомендовать композиции, выбирая названия тех файлов, у которых значения близки к 1.

name = 'rock.00087.wav' series = pd.DataFrame(similarity_names[name].sort_values(ascending = False)) series = series.loc[(series[name]>0.90)] series = series.drop(name) print("\n*******\nSimilar songs to ", name) print(series.head(5))

Получаем названия рекомендованных композиций и их косинусное сходство.

В дальнейшем было бы интересно получить из аудиофайлов изображения в виде, например, их спектрограмм или мел-кепстральных спектрограмм, а затем используя алгоритмы нейронных сетей классифицировать аудиофайлы. Таким образом, мы сможем работать со звуком, применяя не классический подход, заключающийся в преобразовании данных, а будем работать с визуальным представлением звука. Классификация аудиофайлов с библиотекой Librosa.

И напоследок хочу порекомендовать вам бесплатный урок от моих коллег из OTUS. На занятии преподаватели OTUS расскажут про рекомендательные системы, основанные на контентной фильтрации. А затем вы на практике примените изученные подходы, для построения рекомендательной системы онлайн магазина.

• Зарегистрироваться на бесплатный вебинар