Об одной тестовой задаче

Недавно Youtube (*сайт, нарушающий закон РФ) порекомендовал мне любопытный с различных сторон видеоролик. В нём рассматривалась задача, которую, по словам автора, задали его знакомому на собеседовании при приёме на работу в Apple. Эту задачу его знакомый решить не смог.

Сама задача такая. Имеем структуру данных, представляющую собой односвязный список. В каждом узле списка располагается его уникальный номер (не обязательно в порядке связности списка) и указатель на следующий узел. Необходимо определить, есть ли в этом списке цикл (очевидно, что цикл в односвязном списке может быть максимум один) и если есть, то напечатать номер первого узла этого цикла в порядке обхода списка.

Это было проиллюстрировано следующей картинкой:

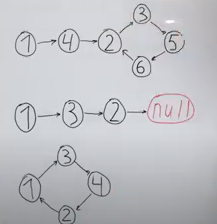
Очевидно, в данных трёх вариантах ответы будут, соответственно, «2», «нет» и «1».

Здесь читателям предлагается придумать свой алгоритм, посмотрев пока на картинку для привлечения внимания.

Следующим шагом зрителям в ролике давалась подсказка: если кто придумал сохранять пройденные узлы в какой-то своей структуре данных и проверять каждый новый узел на присутствие в этой структуре, то такое решение плохое, так как алгоритм не должен требовать O(n) дополнительной памяти.

Настоящим шоком для меня оказалось следующее: больше половины из отметившихся под роликом комментаторов не только не смогло найти решение при указанном ограничении, но и вообще сочло такую задачу имеющей неподъёмную сложность и лишённой практического смысла. По мнению этих людей, данная задача далеко превосходит по своей сложности всё, что когда-либо может понадобиться программисту в жизни.

Это было первое, чем я хотел бы поделиться с читателями. Я просто не могу держать такое знание в себе. Мои представления о типичном уровне людей, профессионально занимающихся программированием, сильно изменились. Конечно, далеко не все смотрят такие ролики, но и не все, наверняка, нашли в себе смелость написать, что они ничего не понимают.

Теперь перейдём к предложенному автором ролика (и, видимо, сообщённому в Apple неудачному претенденту) решению задачи.

Предлагается завести два указателя по схеме «черепаха и кролик», первый из которых продвигается от начала списка со скоростью 1 узел за шаг, а второй – со скоростью 2 узла за шаг. Если список линейный, то второй указатель рано или поздно выйдет на его конец, а если циклический – то указатели рано или поздно встретятся. Далее более тонкими рассуждениями можно показать, что после встречи, если продвигать два указателя по 1 узлу за шаг, начав от начала списка и от места встречи соответственно, то эти указатели встретятся в начале цикла.

Это весьма остроумный алгоритм, однако оправдан ли он? Тут в комментариях развернулись споры между той частью мыслящего меньшинства, которая самостоятельно пришла к такому же алгоритму, и другой частью мыслящего меньшинства, предлагающей метить узлы.

Действительно, более простым решением в предложенной постановке задачи будет такое. Использовать один указатель, и в каждом пройденном узле менять, например, значение номера на отрицательное. Как только мы встретили отрицательное число – это и есть первый узел цикла. Если почему-то мы не хотим жертвовать знаковым битом номера узла, то можем использовать, например, младший или старший биты указателя на следующий узел.

Если нам требуется сохранить список в исходном виде (о чём, заметим, в постановке задачи ничего не сказано), то мы можем сделать дополнительный проход для восстановления наших битиков.

Конечно, возникает некоторое внутреннее сопротивление к модификации списка, переданного в качестве входного параметра. Но заметим, что классики вроде Кнута и Дейкстры зачастую учили программировать именно так, приводя алгоритмы с временным обращением направления связей и тому подобными приёмами.

Сравним эффективность алгоритма кролика-черепахи и алгоритма с маркировкой.

Алгоритм кролика-черепахи не гарантирует нам, что указатели встретятся на первом же обороте цикла, быстрый указатель может сначала перескочить медленный. Поэтому у нас может образоваться лишний проход по циклу. Поскольку нам надо проводить по списку два указателя, то количество операций доступа к памяти и проверки в среднем навскидку где-то около 2*N + 2*L, где N – длина списка, а L – длина цикла. Всё это будут операции чтения.

Алгоритм с маркировкой требует только одного указателя и гарантированно находит начало цикла сразу, поэтому количество операций доступа к памяти и проверки будет N, если мы не восстанавливаем список, и 2*N, если восстанавливаем. Но доступ в данном случае состоит из чтения и записи.

Проверим наши соображения на практике. Запрограммируем алгоритмы на языке Си. В алгоритме кролика и черепахи немножко облегчим себе жизнь и начнём движение указателей сразу со второго шага, чтобы не утяжелять проверку в цикле начальным равенством указателей. Для простоты отрицательный ответ обозначим номером вершины 0.

Алгоритм кролика и черепахи:

#include <stdio.h> #include <time.h>  int main () {    #define SIZE 100000000    struct Node {     long num;     struct Node *next;   };    static struct Node array [SIZE];    long i, time1, time2, loopnode;   struct Node *ptr1, *ptr2;    for (i=0; i<SIZE-1; i++) {     array [i].num = i+1;     array [i].next = &array[i+1];   }   array [SIZE-1].num = SIZE-1;   array [SIZE-1].next = &array[1];    time1 = clock();    ptr1 = &array[1];   ptr2 = &array[2];    while ((ptr2 != NULL) &&          (ptr2->next != NULL) &&          (ptr1 != ptr2)) {     ptr1 = ptr1->next;     ptr2 = ptr2->next->next;   }        if (ptr1 != ptr2)     loopnode = 0;   else {     ptr1 = &array[0];     while (ptr1 != ptr2) {       ptr1 = ptr1->next;          ptr2 = ptr2->next;     }     loopnode = ptr1->num;   }       time2 = clock();      printf ("Loopnode is %ld, time is %ld\n",            loopnode, time2-time1);      return 0;  }

Алгоритм с маркировкой:

#include <stdio.h> #include <time.h>  int main () {    #define SIZE 100000000   #define RESTORE Y    struct Node {     long num;     struct Node *next;   };    static struct Node array [SIZE];    long i, time1, time2, loopnode;   struct Node *ptr1, *ptr2;    for (i=0; i<SIZE-1; i++) {     array [i].num = i+1;     array [i].next = &array[i+1];   }   array [SIZE-1].num = SIZE-1;   array [SIZE-1].next = &array[1];    time1 = clock();    ptr1 = &array[0];    while ((ptr1->num > 0) && (ptr1->next != NULL)) {     ptr1->num = -ptr1->num;     ptr1 = ptr1->next;   }        if (ptr1->next == NULL)     loopnode = 0;   else     loopnode = -ptr1->num;    #ifdef RESTORE      ptr1 = &array [0];   while ((ptr1 != NULL) && (ptr1->num < 0)) {     ptr1->num = -ptr1->num;     ptr1 = ptr1->next;   }      #endif    time2 = clock();    printf ("Loopnode is %ld, time is %ld\n",            loopnode, time2-time1);    return 0;      }

Откомпилируем их при помощи Apple clang 14.0.3 и посчитаем время выполнения на Mac mini с процессором Intel Core i3 3.6 GHz.

Таким образом, более простой алгоритм маркировки с восстановлением не только существенно не уступает кролику и черепахе по производительности, но и в ряде случаев превосходит. А маркировка без восстановления лучше кролика и черепахи вдвое (так как зарплату платить надо одной черепахе).

Какие мысли имеются у читателей по данному поводу?

P.S. Слава богу, есть на свете много умных людей, судя по комментариям. А то я реально испугался, глядя на ютуб.