Проектирование алгоритма под рекомендательную систему

Всем привет! Меня зовут Дмитрий Дивин, я хотел бы поделиться своим опытом проектирования алгоритма для рекомендательной системы.

Примерно два месяца назад я начал интересоваться рекомендательными системами и способами их реализации.

Есть некоторые идеи и неплохие результаты, с которыми я бы хотел поделиться.

Постановка задачи

С точки зрения пользователя, моя задача выглядит следующим образом.
Одна группа пользователей публикует посты, в которых имеется следующий контент:

• Заголовок

• Теги

• Картинки

Другая группа пользователей взаимодействует с этим постами и тем самым накапливает опыт, который в последующем и используется, чтобы сформировать рекомендацию.
Мой проект, для которого я проектирую рекомендательную систему, должен соблюдать следующие требования согласно моей доменной области:

1. Рекомендации должны предлагаться через взаимодействие пользователя с контентом.

2. В рекомендациях не нужно учитывать интересы других пользователей.

3. Старый опыт взаимодействия с контентом должен отбрасываться через неделю, а возможно и через несколько дней.

4. Низкое время отклика рекомендации: любое взаимодействие с контентом должно тут же попадать в рекомендацию

Забегая вперед, мне удалось решить эту задачу с помощью графовой базы Neo4J и получить отличный latency для рекомендаций в реальном времени. Хочу отдать должное разработчикам этой базы за то, что это отличный продукт, для того чтобы понять, что такое графовые базы. Это был мой первый опыт работы с таким типом баз данных, но я уверяю Вас, что подход, который я опишу ниже, можно реализовать и на обычных реляционных базах.

Модель данных

Моя модель данных и их связи выглядят следующим образом. Посты связаны с классификаторами через связь один ко многим. В качестве классификаторов я использовал ключевые слова. Предполагается, что теги, описание картинок и заголовок, должны соответствовать какому-то набору ключевых слов. Таким образом эти связи и образуются.

Пользовательский опыт можно описать следующем образом.

При каждом взаимодействии с постом берутся все классификаторы этого поста и суммируются очки взаимодействия с уже существующим пользовательским опытом.
Очки события — это эмоциональные признаки. Чем выше эмоция у пользователя, тем выше очки взаимодействия.

Эмоциональные признаки можно описать следующим образом:

• Удержать внимание на посте +1 очко

• Поставил лайк посту +2 очка, и т.д.

Можем рассмотреть пример накопления очков подробней, который может понять данный подход.

Предположим, что у пользователя еще нет опыта и ему попался интересующий его пост, на котором он удержал внимание.

У этого поста есть три связи на классификаторы: sky, ocean и nature, значит пользователю добавится следующий опыт: sky(+1), ocean(+1), nature(+1).

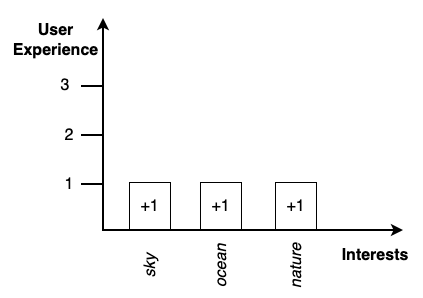
Затем пользователь лайкнул следующий пост, у которого есть две связи на классификаторы: mountain, nature.

Складываем его с уже существующем опытом и получаем: sky(1), ocean(1), nature(1+2), mountain(+2).

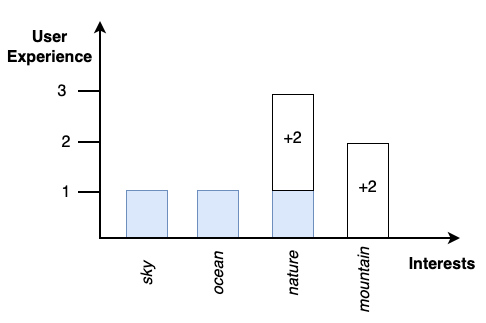
Данную статью можно было бы и не писать, если бы мое внимание не зацепилось за алгоритм косинусного сходства: он еще известен как коэффициент Отиаи. И тут сразу же пришла идея об использовании его в своей задаче.

Описание алгоритма

Алгоритм будет возвращать коэффициент попадания пользовательского опыта в пост, и он будет лежать в диапазоне от 0 до 1 , где: 0 — полный промах, 1 — полное попадание, а значение между 0 и 1 будем считать частичным попаданием.

Для получения релевантности попадания пользовательского опыта в пост подготовим два вектора: один вектор будет описывать пользовательский опыт, а другой — дистанцию к этим классификаторам от максимума к минимуму.

Перед тем, как мы заполним наши вектора, нам нужно сделать объединение наших классификаторов между пользовательским опытом и постом с соблюдением следующих условий:

• Для первого вектора:

  • все классификаторы пользовательского добавляются как есть.

  • если классификатор из поста в пользовательском опыте отсутствует, значит пользовательский опыт для этого классификатора будет равен нулю.

• Для вектора с которым будем сравнивать:

  • все классификаторы поста двигаются к максимуму.

  • если классификатор в посте отсутствует из пользовательского опыта, значит он будет двигаться к минимуму т.е к нулю.

Разберем пример

Предположим, что у пользователя есть следующий накопленный опыт:
sky(1), ocean(1), nature(3), mountain(2)
А пост содержит следующие классификации:
mountain, alp

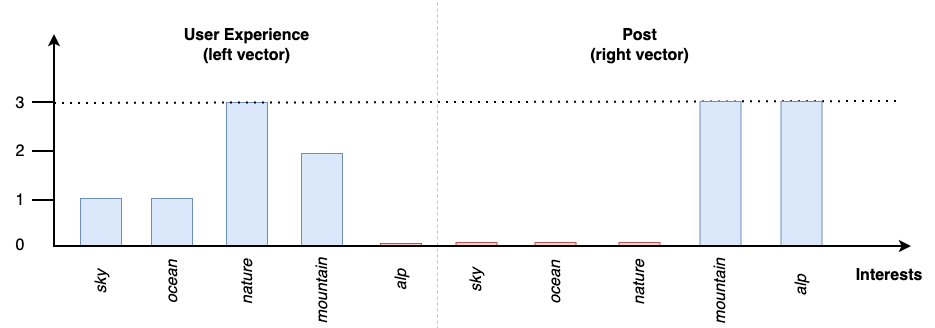
Результат для первого вектора будет равен:
sky(1), ocean(1), nature(3), mountain(2), alp(0)

Результат для второго вектора, с которым будем сравнивать, будет равен:
sky(0), ocean(0), nature(0), mountain(3), alp(3)

Остается только вычислить косинус угла.
cosine([1,1,3,2,0], [0,0,0,3,3]) = 0.365148

Этот алгоритм хорошо работает только тогда, когда у постов точное совпадение классификаторов. А что делать, когда у постов есть признак частичного соответствия?

Например, алгоритмы нейронной сети распознали ключевые слова на картинке с вероятностью:

• nature 98.9%

• mountain 3.6%

Для этого случая пришлось немного доработать данный алгоритм, и у меня получилась следующая версия.

Добавляем к нашим классификаторам признак соответствия от 0 до 1. Очевидно то, что 0 не может быть признаком соответствия и это зависит от доменной области. В своем проекте я использовал классификаторы с признаками соответствия, которые лежали в диапазоне от 0.15 до 1 , где — 1 была полным соответствием, а 0.15 — минимальным.

Доработка алгоритма была в следующем.

Для второй части вектора применим те самые действия, что и для первого, и уравновесим их, приводя их максимумы к одному общему знаменателю по следующей формуле: n/max(n).

Таким образом, максимальный признак будет равен 1, а все другие относительно максимума.

Разберем пример

Предположим, что у пользователя есть следующий опыт:
sky(1), ocean(1), nature(3), mountain(2)

Пост содержит следующие классификаторы с признаками соответствия:
mountain(0.96), alp(0.85)

Результат для первого вектора будет равен:
sky(1/3=0.33333333333), ocean(1/3=0.33333333333), nature(3/3=1), mountain(2/3=0.66666666666), alp(0.0)

Результат для второго вектора, с которым будем сравнивать, будет равен:
sky(0.0), ocean(0.0), nature(0.0), mountain(0.96/0.96=1.0), alp(0.85/0.96=0.88541666666)

Остается только вычислить косинус угла:
cosine([0.33333333333,0.33333333333,1.0,0.66666666666,0.0], [0.0,0.0,0.0,1.0,0.88541666666]) = 0.386626

Анализ алгоритма

У алгоритма есть линейная сложность o(n).
Так как алгоритм основан на косинусном сравнении, то он унаследует и проблему энтропии, но для рекомендаций это и погрешностью считать сложно.

Реализацию данного алгоритма я выложил в своем GitHub аккаунте в виде функции плагина к Neo4j. Там же можно найти и примеры использования.

В следующей публикации я хотел бы рассказать об ограничениях алгоритма, как с ними бороться и поделиться интересной методикой, с помощью которой можно достать рекомендацию из любого количества данных за разумный latency.

Прошу меня не сильно критиковать за оформление моей первой публикации, обещаю что каждая следующая будет еще лучше.