Collaborative Filtering — подход, основанный на отношениях между пользователями (users) и товаром (items), при этом нет никакой информации о пользователях или товарах.
Взаимодействие между пользователем и товаром разделят на две категории:
-
Явное взаимодействие. Например, рейтинг, который пользователь ставит товару.
-
Неявное взаимодействие. Например, клик, просмотр или покупка товара не очевидны с точки зрения рейтинга.
User-item matrix — это таблица, в которой каждая строка представляет собой пользователя, каждый столбец — товар, а каждая ячейка содержит информацию о взаимодействии между пользователем и товаром. Например, в ячейке может быть указано количество раз, которое пользователь купил товар, или оценка, которую пользователь поставил товару. User-item matrix используется в рекомендательных системах для определения предпочтений пользователей и предложения им наиболее подходящих товаров. Очевидно, что user-item matrix — очень большая и разряженная матрица.

Для таких задач применяют матричную факторизацию (представление user-item matrix в виде произведения двух или более матриц более простого вида).
Часто матричная факторизация применяется для уменьшения размерности, где мы пытаемся уменьшить количество элементов, сохраняя при этом соответствующую информацию.
Так дело обстоит с основным компонентным анализом (PCA) и разложение по сингулярному значению (SVD).
где — user-item matrix,
— диагональная матрица с неотрицательными сингулярными числами,
и
— ортогональные матрицы и
.
PCA — один из основных способов уменьшить размерность данных, потеряв наименьшее количество информации. Вычисление главных компонент может быть сведено к вычислению SVD разложения матрицы данных или к вычислению собственных векторов и собственных значений ковариационной матрицы исходных данных.
Математическое содержание метода главных компонент — это SVD разложение ковариационной матрицы, то есть представление пространства данных в виде суммы взаимно ортогональных собственных подпространств
, а самой матрицы
— в виде линейной комбинации ортогональных проекторов на эти подпространства с коэффициентами
.
Оставив -первых (главных) компонент (
) в SVD разложении, получим наиболее точное приближение к
по норме Фробениуса.
За «Скрытым текстом» пример использования SVD и PCA.
Hidden text
Наглядно как работает SVD и PCA.
import numpy as np from matplotlib import image from matplotlib import pyplot as plt import cv2img = image.imread("photo.jpg") plt.imshow(img) plt.show()
Для работы с меньшей размерностью перейдем к черно-белому изображению.
gray_img = cv2.cvtColor(img, cv2.COLOR_RGB2GRAY) plt.imshow(gray_img, cmap='gray') plt.show()
gray_img.shape (558, 563)Применим SVD разложение
U, lmbd, V = np.linalg.svd(gray_img) U.shape, lmbd.shape, V.shape ((558, 558), (558,), (563, 563))S = np.zeros((U.shape[1], V.shape[0])) S[ : U.shape[1], : U.shape[1]] = np.diag(lmbd) S.shape (558, 563)Вернем как было, убедимся что ничего не изменилось
plt.imshow(U @ S @ V, cmap='gray') plt.show()
Попробуем оставить первые 100 компонент и посмотрим насколько изменится качество изображения.
d = 100 U_crop = U[:, :d] S_crop = S[:d, :d] V_crop = V[:d, :] plt.imshow(U_crop @ S_crop @ V_crop, cmap='gray') plt.show()
Качество картинки почти не изменилось, зато сколько сэкономлено памяти!
Попробуем оставить первые 50 компонент.
d = 50 U_crop = U[:, :d] S_crop = S[:d, :d] V_crop = V[:d, :] plt.imshow(U_crop @ S_crop @ V_crop, cmap='gray') plt.show()
Оставим первые 10 компонент.
d = 10 U_crop = U[:, :d] S_crop = S[:d, :d] V_crop = V[:d, :] plt.imshow(U_crop @ S_crop @ V_crop, cmap='gray') plt.show()
Сингулярные числа в матрице S расположены по убыванию: чем ближе к началу, тем компоненты важнее и сильнее влияют на качество изображения.
Уберем первые 5 компонент.
k = 5U_crop = U[:, k:] S_crop = S[k:, k:] V_crop = V[k:, :] plt.imshow(U_crop @ S_crop @ V_crop, cmap='gray') plt.show()
Качество картинки значительно хуже.
Представим нашу user-item matrix как произведение следующих матриц:
Тогда ‑aя строка
— это представление
‑го пользователя, а
‑ый столбец
— представленте
‑го товара. Их отношение (рейтинг) выражается с помощью скалярного произведения:
Матрицы и
найдем с помощью градиентного спуска.
В качестве возьмем
без регуляризации для простоты:
Посчитав градиенты по и по
, получим формулы обновления весов:
k пробегает от 1 до d, где d — число главных компонент.
Продемонстрируем работу алгоритма. Пусть нам заданы пользователи и их оценки к просмотренным фильмам. Задача — спрогнозировать незаполненные ячейки user-item matrix.
import numpy as np import pandas as pdЗададим пользователей и фильмы:
k = 10 # максимальная оценка movies = ['Фантазия', 'ВАЛЛ-И', 'Пиноккио', 'Бемби' , 'Шрэк', 'Дамбо', 'Спасатели', 'Геркулес', 'Кунг-фу Панда'] m_movies = len(movies) users = ['Андрей', 'Аня', 'Алиса', 'Ваня', 'Леша', 'Оксана', 'Саша', 'Паша', 'Сеня', 'Гриша'] n_users = len(users)Оценки раскидаем случайным образом. С учетом чтобы пара user-movie не повторялась
RANDOMSEED = 42 np.random.seed(42) N = np.random.randint(50, 60) # сколько оценок будет поставлено ind_users, ind_movies, rating = [], [], [] user_movie = [] # чтобы пара user-movie не повторялись for _ in range(N): user = np.random.randint(0, n_users) movie = np.random.randint(0, m_movies) if not [user, movie] in user_movie: ind_users.append(user) ind_movies.append(movie) rating.append(np.random.randint(1, k)) # случайная оценка пользователя фильму user_movie.append([user, movie]) N = len(user_movie) def get_user_item_matrix(n_users, m_movies, ind_users, ind_movies, rating): R = [[0] * m_movies for _ in range(n_users)] N = len(ind_users) for i in range(N): R[ind_users[i]][ind_movies[i]] = rating[i] R = np.array(R) return R R = get_user_item_matrix(n_users, m_movies, ind_users, ind_movies, rating) pd.DataFrame(R, users, movies) 
Ошибку будем считать как:
def MSE(R, U, V): mse = 0 for ind in range(N): i = ind_users[ind] j = ind_movies[ind] mse += ( R[i][j] - np.dot(U[i,:], V[:,j]) )**2 / N return mseИспользовать будем стохастический градиентный спуск c фиксированным шагом step. Сделаем n_iters итераций.
def SVD(ind_users, ind_movies, R, d, step, n_iters): # инициализация матриц разложения P = np.random.rand(R.shape[0], d) Q = np.random.rand(d, R.shape[1]) start_mse = MSE(R, P, Q) # Стохастический градиентный спуск for n in range(n_iters): ind = np.random.randint(0, N) i = ind_users[ind] j = ind_movies[ind] for k in range(0, d): P[i, k] = P[i, k] + step * (R[i][j] - P[i, :] @ Q[:, j]) * Q[k, j] Q[k, j] = Q[k, j] + step * (R[i][j] - P[i, :] @ Q[:, j]) * P[i, k] mse = MSE(R, P, Q) return P, Q, start_mse, mse P, Q, start_mse, mse = SVD(ind_users, ind_movies, R, 3, 0.1, 3000) start_mse, mse (22.327189007469947, 0.9592817343783187)Спрогнозируем user-item matrix
R_pred = np.zeros((R.shape[0], R.shape[1])) for i in range(n_users): for j in range(m_movies): R_pred[i][j] = round(P[i,:] @ Q[:,j], 2) pd.DataFrame(R_pred, users, movies)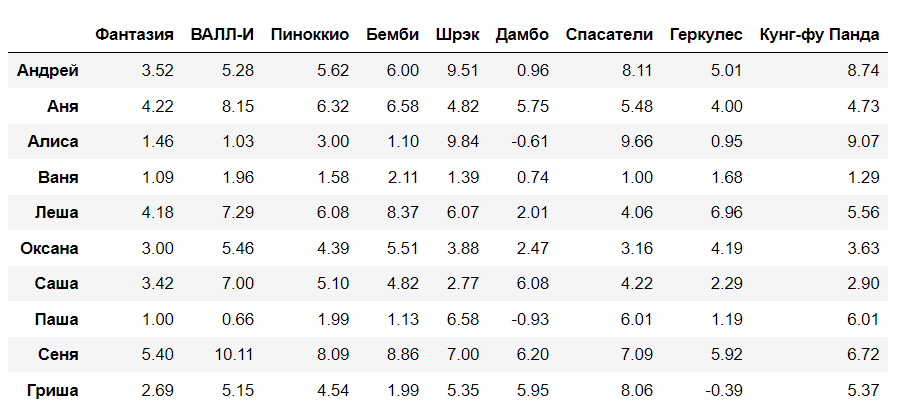
# Вывод еще раз для сравнения pd.DataFrame(R, users, movies)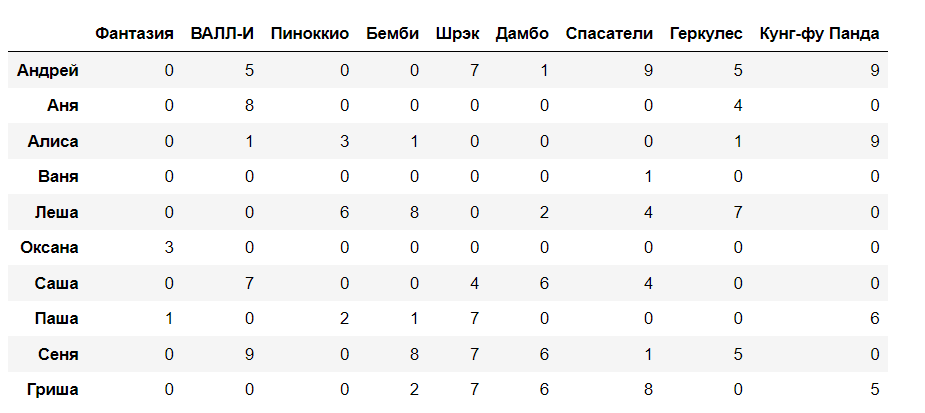
ссылка на оригинал статьи https://habr.com/ru/articles/751470/
Добавить комментарий